Persamaan Navier-Stokes menggambarkan fenomena sederhana sehari-hari, seperti air yang mengalir dari selang kebun - namun, mereka didasarkan pada masalah yang solusinya diperkirakan mencapai satu juta dolar

Dalam fisika, ada persamaan yang menggambarkan segala sesuatu dari peregangan ruangwaktu hingga penerbangan foton. Namun, hanya satu set persamaan yang dianggap begitu rumit secara matematis sehingga ia dipilih sebagai salah satu dari tujuh "
Masalah Milenium ", di mana
Clay Institute of Mathematics menawarkan hadiah satu juta dolar: ini adalah
persamaan Navier-Stokes yang menggambarkan aliran cairan.
Baru-baru ini, saya
menulis tentang bagaimana hasil baru yang penting diperoleh untuk persamaan ini. Dan karya ini menunjukkan bahwa kemajuan menuju Hadiah Milenium akan lebih sulit dari yang diharapkan. Mengapa persamaan ini menggambarkan fenomena yang sudah dikenal seperti air yang mengalir melalui selang secara matematis lebih sulit untuk dipahami daripada, misalnya, persamaan medan Einstein, yang mencakup benda-benda menakjubkan seperti lubang hitam?
Jawabannya, seperti yang saya mengerti, terletak pada turbulensi. Kita semua mengalami fenomena ini, dalam penerbangan di udara tidak homogen pada ketinggian 10.000 m, atau ketika mengamati corong dari air meninggalkan saluran pembuangan di bak mandi. Namun, pengetahuan tidak mengikuti dari kesadaran: turbulensi adalah salah satu bidang dunia fisik yang paling sedikit dipahami.
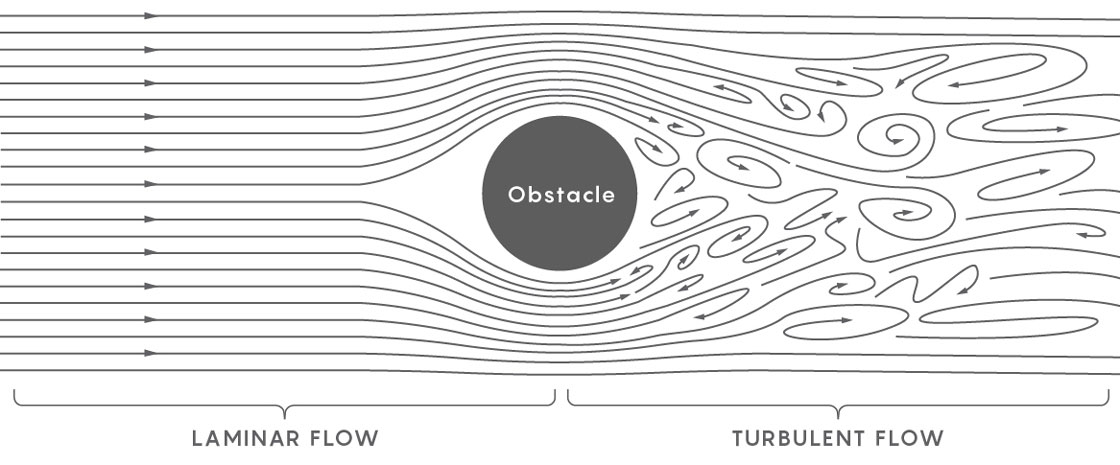
Contoh aliran tanpa turbulensi adalah sungai yang tenang. Setiap bagiannya bergerak ke arah yang sama dengan kecepatan yang sama. Cairan bergolak muncul ketika aliran sungai pecah sehingga berbagai bagian aliran mulai bergerak ke arah yang berbeda dengan kecepatan yang berbeda. Fisikawan menggambarkan pembentukan turbulensi pada awalnya sebagai penampilan corong dalam aliran yang halus, dan kemudian sebagai pembentukan corong kecil di corong pertama, dan corong yang lebih kecil di corong ini - lautan corong yang masuk ke dalam cairan, sehingga cairan tersebut pecah menjadi bagian-bagian yang terpisah, masing-masing berinteraksi satu sama lain dan bergerak ke arahnya sendiri.
Para peneliti ingin memahami dengan tepat bagaimana aliran halus pecah menjadi turbulensi turbulensi, dan memodelkan bentuk fluida di masa depan setelah turbulensi mengambil korban. Tetapi Tantangan Milenium dirumuskan lebih sederhana: Anda hanya perlu membuktikan bahwa solusi selalu ada. Yaitu, pertanyaannya adalah, dapatkah persamaan menggambarkan fluida apa pun, dengan kondisi awal apa pun, dan masa depan yang sangat jauh?
"Langkah pertama adalah mencoba membuktikan bahwa persamaan memiliki beberapa solusi," kata Charlie Fefferman, ahli matematika di Universitas Princeton. "Ini tidak memberikan pemahaman nyata tentang perilaku cairan, tetapi jika Anda tidak memiliki ini, maka Anda tidak tahu apa-apa."
Jadi bagaimana kita bisa membuktikan adanya solusi? Anda harus mulai dengan memahami mengapa itu tidak terjadi. Persamaan Navier-Stokes menyiratkan perhitungan perubahan dalam jumlah seperti kecepatan dan tekanan. Matematikawan khawatir tentang skenario berikut: Anda melarikan diri persamaan ini, dan setelah waktu yang terbatas mereka memberitahu Anda bahwa partikel cairan bergerak dengan kecepatan tak terbatas. Dan ini masalahnya - menghitung perubahan dalam nilai tak terbatas tidak lebih mudah daripada membaginya dengan nol. Matematikawan menyebut situasi seperti itu sebagai "ledakan", dan jika terjadi ledakan, persamaan berhenti bekerja dan tidak ada solusi yang ditemukan.
 Persamaan Navier-Stokes menggambarkan aliran cairan yang tidak dapat dimampatkan.
Persamaan Navier-Stokes menggambarkan aliran cairan yang tidak dapat dimampatkan.
Secara umum, produk dari massa (bagian biru) dan akselerasi (violet) sama dengan gaya yang bekerja pada cairan (oranye):- ρ adalah densitas fluida;
- dV / dt - perubahan kecepatan dari waktu ke waktu;
- V ∇V - kecepatan dan arah gerakan;
- ∇P - perubahan tekanan internal;
- ρ g - pengaruh kekuatan eksternal (misalnya, gravitasi);
- μ ∇ 2 V - pengaruh kekuatan internal (viskositas).
Bukti tidak adanya ledakan (dan adanya solusi) setara dengan bukti bahwa kecepatan maksimum setiap partikel cair tetap dibatasi oleh beberapa nilai terbatas. Salah satu jumlah terpenting adalah energi kinetik dari cairan.
Ketika Anda mulai mensimulasikan aliran menggunakan persamaan Navier-Stokes, cairan Anda memiliki sejumlah energi awal. Dalam aliran turbulen, energi dapat mulai berkonsentrasi. Alih-alih menyebar secara seragam di seluruh sungai, energi kinetik dapat dikumpulkan dalam pusaran air dengan ukuran kecil sembarang, dan partikel-partikel dalam pusaran air ini (secara teoritis) dapat berakselerasi hingga kecepatan tak terbatas.
“Dengan transisi ke skala yang lebih kecil dan lebih kecil, energi kinetik menjadi semakin tidak berguna untuk pengendalian keputusan. Keputusan dapat melakukan apa saja, dan saya tidak tahu bagaimana mengendalikannya, "kata Vlad Vikol, ahli matematika di Universitas Princeton yang menulis sebuah karya baru dengan Tristan Buckmaster.
Matematikawan mengklasifikasikan persamaan diferensial parsial berdasarkan sejauh mana mereka dapat mulai berperilaku buruk pada skala yang sangat kecil. Persamaan Navier-Stokes berada pada ujung ekstrim dari skala ini. Kompleksitas matematika persamaan dalam arti mencerminkan kompleksitas aliran turbulen yang harus dapat mereka gambarkan.
"Ketika Anda memperbesar di beberapa tempat, maka dari sudut pandang matematika, Anda kehilangan informasi tentang solusinya," kata Vikol. "Tapi turbulensi seharusnya menggambarkan hal itu - transfer energi kinetik dari skala besar ke skala yang lebih kecil, jadi itu benar-benar meminta Anda untuk meningkatkannya."

Berbicara tentang sifat matematika dari persamaan fisik, adalah wajar untuk mengajukan pertanyaan: apakah argumen ini akan mengubah cara kita memandang dunia fisik? Dalam kasus persamaan Navier-Stokes dan Masalah Milenium, jawabannya adalah "ya" dan "tidak". Setelah hampir 200 tahun bereksperimen, jelaslah bahwa persamaan itu bekerja: aliran yang diprediksi oleh Navier-Stokes secara berurutan bertepatan dengan aliran yang diamati dalam eksperimen. Jika Anda seorang fisikawan yang bekerja di laboratorium, ini mungkin cukup untuk Anda. Tapi matematikawan perlu tahu lebih banyak - mereka ingin memeriksa apakah mungkin untuk mengikuti persamaan ini semua cara untuk memantau bagaimana sebenarnya aliran berubah dari satu saat ke waktu (untuk konfigurasi fluida awal), dan bahkan untuk menangkap sumber turbulensi.
"Perilaku cairan penuh dengan kejutan," kata Fefferman. "Kejutan-kejutan ini, pada prinsipnya, dijelaskan oleh persamaan fundamental yang mengontrol aliran fluida, tetapi bagaimana bergerak dari persamaan yang mengontrol gerakan fluida ke deskripsi bagaimana fluida sebenarnya bergerak adalah sebuah misteri."