Dua ahli matematika membuktikan bahwa dalam kondisi ekstrem tertentu persamaan Navier-Stokes memberikan omong kosong
Persamaan Navier-Stokes dengan bantuan beberapa istilah singkat menggambarkan salah satu fenomena paling umum dari dunia fisik: aliran cairan. Saat ini, persamaan ini, yang berasal dari tahun 1820-an, digunakan untuk menggambarkan segala sesuatu mulai dari arus laut dan turbulensi mengikuti pesawat terbang hingga aliran darah ke jantung.
Meskipun fisikawan menganggap persamaan ini dapat diandalkan, seperti palu, matematikawan tidak mempercayai mereka. Bagi seorang ahli matematika, fakta bahwa persamaan ini tampaknya bekerja tidak berarti banyak. Mereka membutuhkan bukti bahwa persamaan itu bebas kesalahan: bahwa untuk setiap cairan dan untuk ramalan jangka panjang, didistribusikan sejauh masa depan, matematika persamaan tidak akan gagal. Tidak mudah menemukan jaminan seperti itu. Orang atau tim pertama yang dapat membuktikan bahwa persamaan Navier-Stokes akan selalu bekerja - atau memberikan contoh yang membuktikan bahwa mereka tidak berfungsi - akan dapat menerima hadiah untuk menyelesaikan salah satu
Masalah Milenium , diumumkan oleh
Clay's Mathematical Institute , dan satu juta dolar dalam Selain [pada 2017, hanya satu dari tujuh tugas milenium (hipotesis Poincaré) telah diselesaikan oleh Gregory Perelman / kira-kira. diterjemahkan.].
Matematikawan telah mengembangkan banyak cara untuk menyelesaikan masalah ini. Karya baru, yang diterbitkan pada bulan September, mengajukan pertanyaan serius tentang apakah salah satu pendekatan paling populer untuk masalah ini, yang dikembangkan selama bertahun-tahun, dapat berhasil. Karya yang ditulis oleh Tristan Buckmaster dan Vlad Vikol dari Princeton University, adalah hasil pertama yang menunjukkan bagaimana, dalam kondisi tertentu, persamaan Navier-Stokes memberikan deskripsi yang kontradiktif tentang dunia fisik.
“Kami mencoba memahami masalah-masalah tertentu yang melekat dalam persamaan ini, dan mengapa orang mungkin harus memikirkannya kembali,” kata Buckmaster.
Karya Buckmaster dan Wikol menunjukkan bahwa jika Anda membuat asumsi yang sangat kasar ketika menyelesaikan persamaan Navier-Stokes, mereka mulai tidak masuk akal: mereka mengatakan bahwa cairan yang sama dengan kondisi awal yang sama dapat muncul di dua atau lebih negara bagian yang berbeda. Itu dapat mengalir dalam satu cara, atau dengan cara yang sama sekali berbeda. Jika demikian, maka persamaan-persamaan ini tidak dapat secara andal menggambarkan dunia fisik tempat mereka dikembangkan.
Meledak persamaan
Untuk memahami bagaimana persamaan dapat pecah, bayangkan arus samudera. Dalam kerangka kerjanya, arus lokal dapat eksis, sebagai akibatnya beberapa bagiannya dapat bergerak dalam satu arah dan pada satu kecepatan, dan lainnya pada arah lain pada kecepatan lain. Aliran lokal berinteraksi satu sama lain dalam aksi saling gesekan dan tekanan air, yang menentukan alirannya.
Matematikawan memodelkan interaksi ini menggunakan peta yang memberi tahu Anda tentang arah dan laju aliran pada titik mana pun dalam fluida. Peta ini, yang disebut bidang vektor, adalah potret dinamika internal fluida. Persamaan Navier-Stokes mengambil gambar ini dan mereproduksinya sebagai video, mengatakan bagaimana tepatnya bidang vektor akan terlihat pada setiap momen berikutnya dalam waktu.
Peta angin (windy.com) bekerja dengan cara yang mirip dengan bidang vektor. Di setiap titik, angin memiliki arah dan kekuatan tertentu.Persamaan ini bekerja. Mereka menggambarkan aliran fluida andal seperti persamaan Newton yang memprediksi posisi planet di masa depan; fisikawan terus-menerus menggunakannya, dan mereka terus-menerus bertepatan dengan hasil eksperimen. Namun, matematikawan membutuhkan lebih dari konfirmasi episodik - mereka membutuhkan bukti bahwa persamaan tidak rusak, tidak peduli apa bidang vektor yang Anda mulai, dan seberapa jauh Anda mereproduksi di masa depan, persamaan akan selalu memberi Anda bidang vektor baru dan unik.
Ini adalah tema Masalah Milenium, menanyakan apakah persamaan Navier-Stokes memiliki solusi (solusi, pada kenyataannya, adalah bidang vektor) untuk semua titik awal di semua titik waktu. Solusi ini harus memastikan arah dan kekuatan aliran yang tepat pada setiap titik dalam fluida. Solusi yang memberikan informasi dengan resolusi sangat kecil seperti itu disebut "halus". Untuk solusi yang halus, setiap titik bidang memiliki vektor yang terkait dengannya, yang memungkinkan Anda untuk "berjalan lancar" di sekitar bidang tanpa terjebak pada titik-titik di mana vektor tidak ada - pada titik di mana Anda tidak akan mengerti pergerakan selanjutnya.
Solusi halus adalah representasi lengkap dari dunia fisik, tetapi dari sudut pandang matematika, mereka mungkin tidak selalu ada. Matematikawan yang mengerjakan persamaan seperti ini mengkhawatirkan situasi ini: Anda menjalankan persamaan Navier-Stokes dan mengamati perubahan dalam bidang vektor. Setelah waktu yang terbatas, persamaan memberi tahu Anda bahwa partikel cairan tertentu bergerak dengan kecepatan tak terbatas. Maka Anda akan memiliki masalah. Persamaannya termasuk mengukur perubahan sifat-sifat seperti tekanan, gesekan, dan kecepatan fluida - dalam bahasa jargon, mereka mengambil turunan dari jumlah ini - tetapi tidak lebih mudah untuk mengambil turunan dari jumlah tak terbatas daripada membaginya dengan nol. Jadi jika persamaan memberikan nilai tak terbatas, kita dapat mengatakan bahwa mereka menolak Anda, atau "meledak". Mereka tidak bisa lagi menggambarkan keadaan cairan Anda selanjutnya.
"Ledakan" semacam itu adalah bukti bahwa persamaan tidak memiliki deskripsi dari beberapa sifat dunia fisik yang harus mereka gambarkan. "Mungkin persamaan tidak mencakup semua efek dari fluida nyata, karena dalam fluida nyata kita tidak mengharapkan kecepatan partikel tak terbatas," kata Buckmaster.
Solusi untuk Masalah Milenium adalah dengan menunjukkan bahwa persamaan Navier-Stokes tidak pernah meledak, atau untuk menemukan kondisi di mana ini terjadi. Salah satu strategi yang digunakan oleh ahli matematika adalah melunakkan persyaratan untuk seberapa akurat persamaan ini harus menggambarkan solusi yang diperlukan.
Gangguan aliran
Persamaan Navier-Stokes harus menggambarkan aliran fluida apa pun, dengan kondisi awal apa pun, dan memperluas uraian yang jauh ke masa depan. Mencoba membuktikan kemampuan ini, matematikawan kadang-kadang "melemah", yaitu, mereka menggunakan deskripsi perkiraan bidang vektor yang menggambarkan fluida. Tetapi ada kesulitan dengan ini.
Idealnya, matematikawan ingin membuktikan bahwa menerapkan persamaan Navier-Stokes pada fluida “halus” terus menerus akan menghasilkan satu hasil unik.
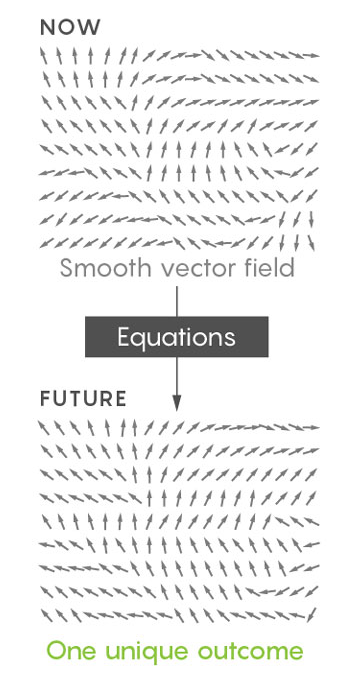
Namun, lebih mudah untuk bekerja dengan "lemah", bidang vektor tidak begitu rinci. Dan ahli matematika telah menemukan bahwa beberapa deskripsi yang lemah menghasilkan hasil yang tidak unik - mereka memungkinkan cairan yang sama mengalir dalam kondisi awal yang sama dalam dua cara.
Dari lemah ke halus
Ketika ahli matematika mempelajari persamaan seperti ini, mereka kadang-kadang mulai memperluas definisi tentang apa yang merupakan solusi. Solusi halus membutuhkan informasi maksimum - dalam kasus Navier-Stokes, mereka mengharuskan pada setiap titik dalam bidang vektor yang terkait dengan cairan vektor ada. Tetapi bagaimana jika kita melonggarkan persyaratan dan mengatakan bahwa Anda perlu menghitung vektor hanya untuk beberapa titik lapangan, atau Anda hanya perlu mendapatkan nilai perkiraan vektor saja? Keputusan semacam itu disebut "lemah." Mereka memungkinkan matematikawan untuk merasakan perilaku persamaan tanpa pekerjaan yang membosankan untuk menemukan sepenuhnya semua solusi (yang dalam praktiknya mungkin tidak mungkin).
Tristan Buckmaster, ahli matematika Universitas Princeton"Dari beberapa sudut pandang, keputusan yang lemah bahkan lebih mudah untuk digambarkan daripada yang nyata, karena Anda perlu tahu lebih sedikit," kata Camillo De Lellis, penulis bersama dengan Lazlo Schekelikhidi, yang menulis beberapa karya penting yang meletakkan dasar bagi karya Buckmaster dan Vikola.
Solusi yang lemah ada di berbagai tingkatan. Jika Anda membayangkan solusi yang halus dalam bentuk gambar matematika dari cairan dengan resolusi tak terbatas, maka solusi yang lemah akan menjadi seperti versi 32-bit, 16-bit atau 8-bit dari gambar ini.
Pada tahun 1934, ahli matematika Prancis
Jean Leray mendefinisikan kelas penting dari solusi lemah. Alih-alih bekerja dengan vektor yang tepat, "solusi Leray" mengambil nilai rata-rata vektor di lingkungan kecil bidang vektor. Leray membuktikan bahwa Anda selalu dapat menyelesaikan persamaan Navier-Stokes, memungkinkan keputusan Anda untuk mengambil bentuk seperti ini. Dengan kata lain, keputusan Lera tidak meledak.
Prestasi Lera menentukan pendekatan baru untuk masalah Navier-Stokes: mulai dengan solusi Lera, keberadaannya sudah diketahui, dan lihat apakah Anda dapat mengubahnya menjadi solusi halus yang keberadaannya ingin Anda buktikan. Proses ini mirip dengan yang Anda mulai dengan gambaran kasar, dan lihat apakah Anda dapat memutar resolusi secara bertahap untuk mencapai gambar kenyataan yang sempurna.
"Salah satu strategi yang mungkin adalah menunjukkan bahwa keputusan Lera yang lemah ini mulus, dan jika Anda dapat menunjukkan bahwa itu mulus, Anda akan menyelesaikan Tantangan Millenium," kata Bakmaster.
Vlad Vkol mewakili setengah dari tim yang mengungkapkan masalah dalam pendekatan untuk memeriksa persamaan Navier-Stokes.Ada lagi tangkapan. Solusi dari persamaan Navier-Stokes sesuai dengan peristiwa fisik nyata, dan peristiwa fisik terjadi dalam satu cara yang mungkin. Dengan ini, saya ingin persamaan Anda hanya memiliki satu set solusi unik. Jika persamaan memberi Anda banyak solusi yang mungkin, mereka tidak dapat melakukan pekerjaan mereka.
Oleh karena itu, matematikawan akan dapat menggunakan solusi Leray untuk memecahkan Masalah Milenium, hanya jika solusi Leray unik. Solusi Leray non-unik akan berarti bahwa, menurut aturan Navier-Stokes, cairan yang sama dengan kondisi awal yang sama dapat datang ke dua keadaan fisik yang berbeda, yang tidak memiliki makna fisik, dan menyiratkan bahwa persamaan tidak benar-benar menggambarkan apa yang seharusnya.
Hasil baru Bakmaster dan Wikol adalah petunjuk pertama bahwa untuk definisi tertentu dari keputusan yang lemah ini dapat terjadi.
Banyak dunia
Dalam karya baru mereka, Buckmaster dan Wikol mempertimbangkan solusi yang bahkan lebih lemah daripada solusi Leray - solusi yang menggunakan prinsip rata-rata yang sama dengan Leray, tetapi melemahkan satu persyaratan tambahan lagi (dikenal sebagai ketimpangan energi). Mereka menggunakan metode "integrasi cembung", yang berasal dari pekerjaan pada geometri ahli matematika John Nash, dan kemudian terlibat dalam studi cairan oleh De Lellis dan Schekelikhidi.
Menggunakan pendekatan ini, Buckmaster dan Wikol membuktikan bahwa solusi yang sangat lemah dari persamaan Navier-Stokes ini tidak unik. Mereka, misalnya, menunjukkan bahwa jika Anda mulai dengan cairan yang benar-benar tenang, misalnya, dengan segelas air di sebelah tempat tidur, dua jenis peristiwa mungkin terjadi. Yang pertama jelas: air dimulai dengan keadaan tenang dan selalu tetap tenang. Yang kedua adalah fantastis, tetapi secara matematis dimungkinkan: air mulai dari keadaan tenang, meledak di tengah malam, dan kemudian kembali ke keadaan tenang.
"Ini membuktikan kurangnya keunikan, karena setidaknya dua objek dapat dibangun dari data awal," kata Vikol.
Buckmaster dan Wikol membuktikan adanya banyak solusi lemah yang tidak unik (tidak hanya dua yang dijelaskan di atas) dari persamaan Navier-Stokes. Pentingnya bukti ini masih harus dipahami. Pada titik tertentu, solusi yang lemah dapat menjadi sangat lemah sehingga tidak lagi terkait dengan solusi yang lebih halus yang harus ditiru. Jika demikian, maka hasil yang diperoleh Bakmaster dan Wikol akan sedikit.
“Hasil ini jelas merupakan peringatan, tetapi orang dapat berargumen bahwa peringatan ini menyangkut ide terlemah dari keputusan yang lemah. Ada banyak lapisan solusi yang lebih kuat yang bisa Anda harapkan untuk perilaku yang jauh lebih baik ”dalam kasus persamaan Navier-Stokes,” kata De Lellis.
Backmaster dan Wikol juga berpikir dalam hal lapisan, dan ia mengarahkan pandangannya pada keputusan Lehr - untuk membuktikan bahwa mereka juga mengakui beberapa fisika di mana fluida yang sama dari keadaan yang sama dapat datang ke berbagai bentuk di masa depan.
“Tristan dan saya percaya bahwa keputusan Leray tidak unik. Kami belum membuktikan ini, tetapi pekerjaan kami menjadi jembatan untuk serangan pada tugas ini, “kata Vikol.