Lintasan Venus pada piringan Matahari dan penentuan jarak di antara mereka

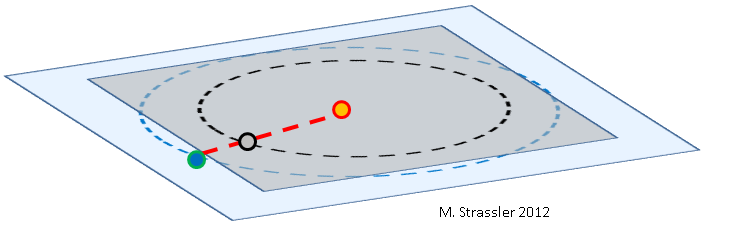
Fig. 1: Bumi (biru), Venus (abu-abu), dan Matahari (oranye), tidak untuk skala.

Mengenai perjalanan Venus melalui piringan Matahari pada 2012, banyak artikel telah ditulis. Tentang seberapa jarang peristiwa ini terjadi, dan mengapa tepatnya: dalam teori, Venus, bergerak mengelilingi Matahari lebih sering daripada Bumi, harus melewati antara Bumi dan Matahari pada setiap belokannya (Gbr. 1), tetapi karena orbit dua planet tidak selaras (mereka tidak berada di bidang yang sama, lihat Gambar. 2), Venus sering melewati di atas atau di bawah Matahari dari sudut pandang Bumi.

Tetapi alih-alih mengulangi kata-kata orang lain, saya ingin menambahkan beberapa detail yang tidak begitu mudah ditemukan di Internet.

Anda mungkin telah membaca bahwa menggunakan teknik yang didasarkan pada alasan astronom Edmund Halley (komet terkenal Halley) yang dibuat olehnya dari tahun 1678 hingga 1716, serta James Gregory kepadanya, jalur Venus pada tahun 1716 digunakan untuk menentukan jarak dari Bumi ke Matahari (dan sebelum Venus, dan semua planet lainnya) dengan kesalahan 2% adalah yang tertinggi yang dicapai pada waktu itu. Diharapkan keakuratannya akan 10 kali lebih tinggi, tetapi efek optik tak terduga yang disebut " efek jatuh hitam " ikut campur dalam proses - masih ada perdebatan tentang alasan yang tepat untuk terjadinya. Tetapi Anda mungkin belum membaca bahwa pengukuran ini - dan banyak pengukuran jarak astronomi lainnya, hingga bintang yang cukup dekat - didasarkan pada prinsip paralaks , pada fakta geometris yang sama yang digunakan mata dan otak kita untuk merasakan kedalaman, atau kemampuan kita untuk merasakan seberapa jauh benda-benda itu dari kita hanya dengan melihatnya.


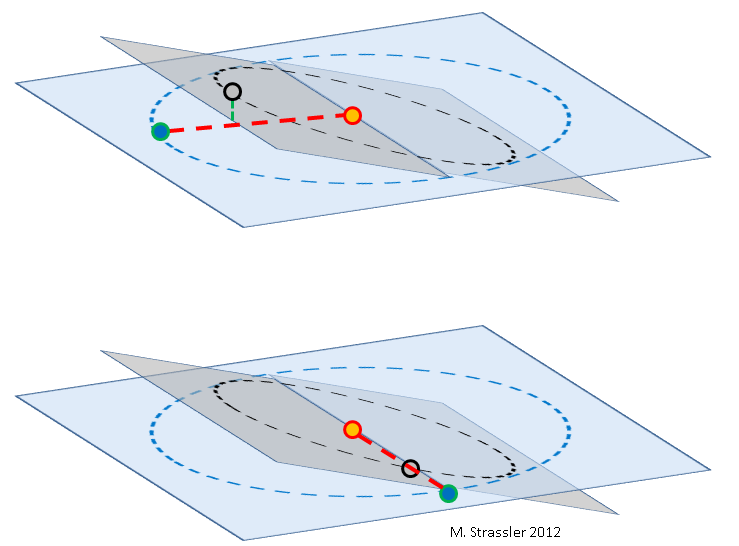Fig. 2: Bumi (biru), Venus (abu-abu) dan Matahari (oranye), tidak untuk skala. Orbit Venus (lingkaran hitam dalam persegi panjang abu-abu) cenderung relatif terhadap orbit Bumi (lingkaran biru dalam persegi panjang biru). Tingkat kemiringannya sangat dilebih-lebihkan. Karena Bumi dan Venus berputar mengelilingi Matahari dengan kecepatan yang berbeda, mereka dapat saling berpapasan di titik mana pun di orbit.

Atas: selama bagian ini, Venus terletak di atas atau di bawah (garis hijau) garis yang menghubungkan Bumi dan Matahari (garis merah), sehingga Venus tidak melewati piringan matahari.

Bawah: Dalam kasus yang jarang terjadi, garis yang menghubungkan Bumi dan Matahari bertepatan dengan garis perpotongan bidang-bidang orbit, dan Venus berada di dekat garis yang sama, yang mengarah ke jalur tersebut.

Tanpa paralaks, juga tidak sulit untuk menentukan jarak relatif dari Venus ke Matahari - yaitu, rasio jari-jari orbit Venus L _V ke jari-jari orbit Bumi L _E. Oleh karena itu, dalam astronomi Renaissance, jarak relatif dari planet ke Bumi dan Matahari dihitung cukup awal. Tetapi untuk menentukan L _V dan L _E secara terpisah, perlu untuk mengukur paralaks, dan bagian dari Venus dapat menyediakannya. Bagian dari Venus pada 1760-an memberikan pengukuran yang cukup akurat L _E - L _V , jarak "absolut" dari Bumi ke Venus; ini memungkinkan untuk menemukan L _E , L _V , dan jarak ke semua planet lain dengan kesalahan beberapa persen. Sebelum ini, pada akhir abad ke-17, pengukuran dilakukan dari jarak dari Bumi ke Mars, yang memiliki kesalahan sekitar 10%; ini juga didasarkan pada paralaks, tetapi ini adalah cerita yang sama sekali berbeda.

Komentar pendahuluan: Bumi dan Venus, dan bahkan Matahari sangat kecil dibandingkan dengan jarak di antara mereka, sehingga hampir tidak mungkin untuk menggambar gambar yang akurat. Dalam ilustrasi, Anda selalu harus menggambar planet yang lebih besar dari yang sebenarnya, sehubungan dengan jarak di antara mereka, hanya agar Anda dapat memahami konsepnya. Ingatlah ini! Semua ilustrasi saya tidak tertarik ke skala.

Ukuran relatif orbit Venus dan Bumi

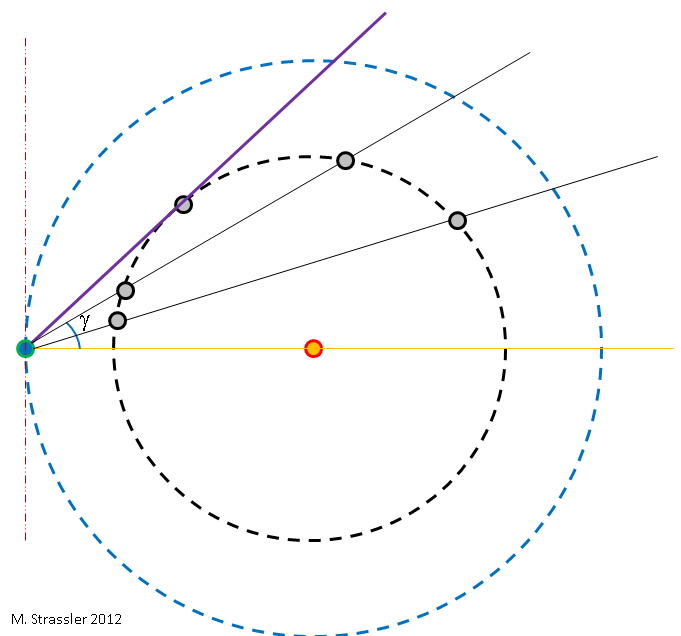Fig. 3

Untuk memahami alasan utama dari kesederhanaan penentuan L _V / L _E , anggaplah bahwa orbit Bumi dan Venus melingkar dan sejajar - mereka terletak di bidang yang sama (seperti yang ditunjukkan pada Gambar. 1, isometrik, dan pada Gambar. 3 adalah "tampilan atas"). Bahkan, orbit Bumi dan Venus sedikit memanjang dan tidak selaras (Gbr. 2). Tetapi eliptisitas dan ketidakcocokan pesawat tidak terlalu penting untuk alasan kami, jadi pertama-tama kita bisa mengabaikannya, dan kemudian ingat lagi untuk mendapatkan jawaban yang lebih akurat.

Di sini kita akan menerapkan teknologi klasik untuk fisika: kita akan membuat perkiraan yang cukup untuk tugas saat ini dan kita tidak akan pergi lebih dalam dari yang diperlukan. Ini adalah cara berpikir yang sangat kuat tentang sains dan pengetahuan secara umum - cukup untuk menjawab pertanyaan apa pun dengan tingkat akurasi tertentu, sehingga Anda dapat menggunakan teknik paling sederhana dari yang akan memberi Anda tingkat akurasi yang diinginkan. Metode ini telah digunakan dengan sempurna selama berabad-abad dan tidak hanya berlaku untuk fisika.

Oleh karena itu, kami akan mengambil perkiraan di mana orbitnya melingkar dan selaras, dan kami akan menerima kira-kira jawaban yang benar, dengan kesalahan beberapa persen. Ini akan cukup untuk menunjukkan konsep dasar, yang saya cari. Percayalah, Anda dapat membuat perhitungan yang jauh lebih akurat - atau Anda bisa menjadi ahli dalam masalah ini sendiri. Tetapi perkiraan kami tidak hanya akan memberikan jawaban yang sangat baik, tetapi juga akan dapat menunjukkan mengapa begitu mudah untuk menghitung rasio L _V ke L _E , tetapi bukan nilai L _V dan L _E sendiri.

Selama tahun ketika Bumi dan Venus berputar mengelilingi Matahari dengan kecepatan yang berbeda, posisi relatif Bumi dan Venus sehubungan dengan Matahari berubah. Jika pada hari tertentu (hari, bulan, tahun) saya memutuskan untuk menggambar dengan Matahari di tengah dan dengan Bumi di sebelah kiri, seperti pada Gambar. 2, maka Venus dapat berada di mana saja di orbitnya. Ini berarti bahwa dari sudut pandang Bumi, sudut antara Venus dan Matahari di langit akan berubah tergantung pada tanggal. Ini ditunjukkan dalam gambar. 3, di mana sudut disebut γ. Sudutnya mudah diukur; temukan Venus di langit setelah matahari terbenam atau sebelum matahari terbit dan ukur sudut antara Venus dan Matahari; lihat gambar 4.


Fig. 4

Dari ara. Gambar 3 menunjukkan bahwa γ memiliki ukuran maksimum - sudut antara garis oranye dan ungu. Bergerak dalam orbit, Venus akan muncul di tempat lain setiap matahari terbenam; untuk beberapa waktu ia akan naik lebih tinggi di atas cakrawala selama beberapa malam berturut-turut, dan kemudian secara bertahap mulai muncul di bawah. Mengamati Venus selama beberapa malam berturut-turut dan mengukur γ, kita dapat menentukan nilai maksimum γ, yang akan saya sebut γ _maks .

Dari ara. 3 jelas bahwa (seperti yang ditunjukkan pada Gambar. 4) γ _maks kurang dari 90 °, karena garis violet harus terletak di antara oranye dan merah, tegak lurus. Secara geometris, ini adalah konsekuensi dari fakta bahwa Venus selalu lebih dekat ke Matahari daripada Bumi. Sudut-sudut ini menjelaskan mengapa Venus selalu terlihat baik segera setelah matahari terbenam atau sebelum matahari terbit (kecuali untuk hari-hari ketika ia berada di belakang Matahari). Venus tidak bisa berada di puncaknya setelah gelap, karena untuk ini ia harus berada di sebelah kiri garis merah.


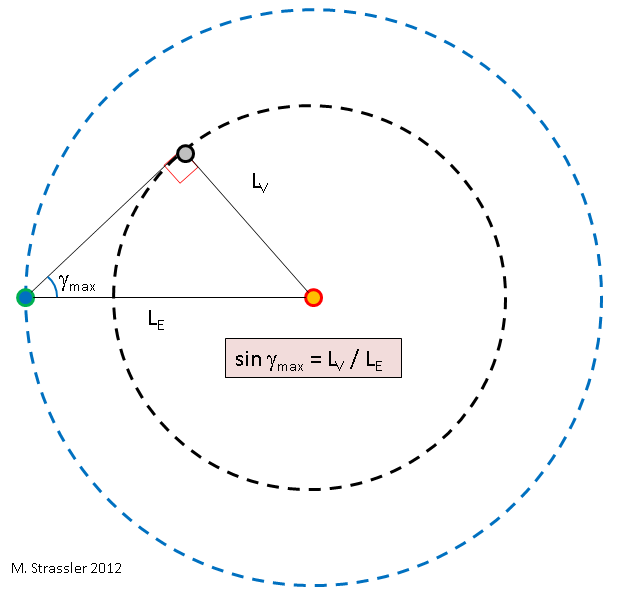Fig. 5

Sekarang kita dapat menentukan rasio jari-jari dua orbit - L _V ke L _E - menggunakan γ _maks . Ini adalah geometri yang paling sederhana, lihat gbr. 5. Intinya adalah bahwa ketika Venus berada pada sudut maksimum dari Matahari, garis antara Matahari dan Venus tegak lurus terhadap garis antara Bumi dan Venus, sehingga garis yang menghubungkan ketiga benda ini membentuk segitiga siku-siku. Dari sini kita dapat menggunakan trigonometri standar:

$$

$$L_V / L_E = \ gamma_ {max}$$

Dan dari sini, dengan bantuan rumus geometris sederhana lainnya, kita mendapatkan hubungan antara jarak ke planet lain.

Ini tidak sepenuhnya akurat, karena alasan yang ditunjukkan di awal; orbit planet adalah elips, dan tidak terletak di bidang air. Dengan kata lain, L _V dan L _E tidak disimpan sepanjang tahun, dan γmax diterapkan sedikit lebih rumit, dalam tiga dimensi, seperti pada Gambar. 2, tetapi tidak dalam dua, seperti pada Gambar. 1, 3 dan 5. Tetapi dengan bantuan pengukuran akurat posisi Venus dan Matahari di langit, dimungkinkan untuk menentukan orbit Venus dan Bumi di sekitar Matahari yang tepat serta meningkatkan perhitungan. Artinya sama; semua pengukuran posisi Venus dan Matahari di langit hanya memungkinkan kita untuk mengukur ukuran relatif orbit Venus dan Bumi. Tetapi nilai yang tepat dari _LV dan L _E tidak dapat ditentukan dengan cara ini. Di sini kita membutuhkan pendekatan yang berbeda.

Lintasan Venus, paralaks, dan jarak ke Matahari

Alasan mengapa perjalanan Venus memungkinkan Anda untuk mengukur nilai absolut orbit Bumi dan Venus adalah bahwa proses ini dapat diamati dengan akurasi tinggi dari berbagai tempat di dunia, sebagai akibatnya Anda akan memiliki dua perspektif tentang lokasi Venus yang terlihat dalam kaitannya dengan Matahari, diukur dari berbagai tempat yang diketahui. jarak di antara mereka. Mengukur paralaks memungkinkan Anda untuk menentukan nilai absolut jarak dari Bumi ke Venus dari sudut paralaks dan jarak antara dua titik pengukuran di Bumi - seperti jenis objek berbeda untuk mata kiri dan kanan memungkinkan otak kita memberi kita kedalaman - rasa jarak dari objek.


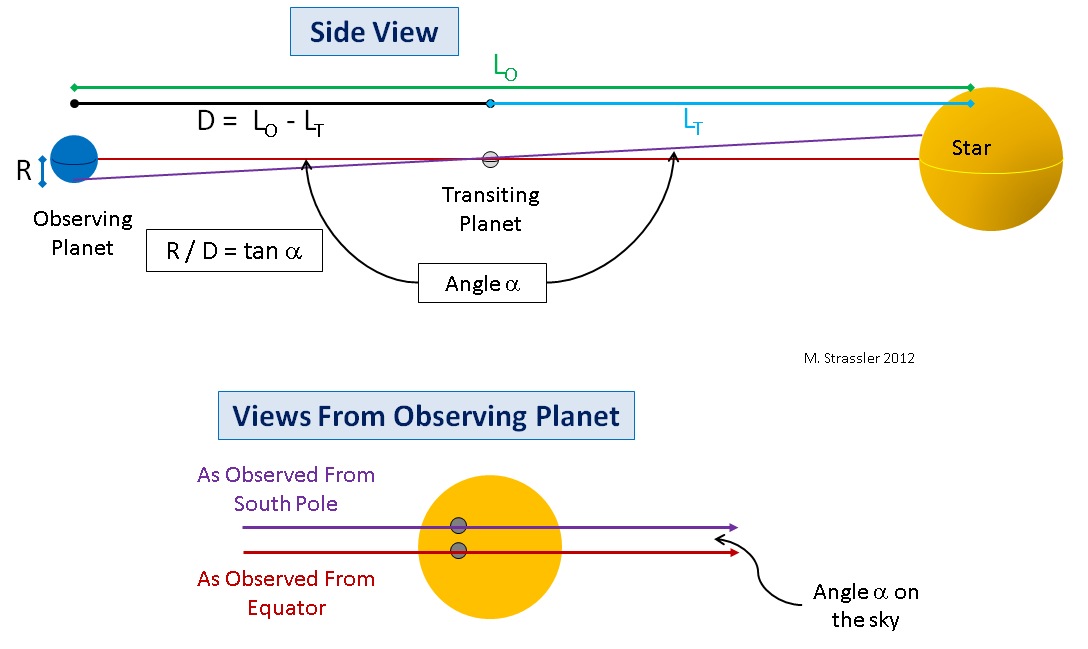Fig. 6

Untuk demonstrasi, izinkan saya menggambarkan bagaimana tampilannya dari planet besar. Dalam gbr. Gambar 6 menunjukkan planet yang dengannya kita akan mengamati bagian (itu akan menjadi Bumi) dan planet yang lewat di depan bintang (itu akan menjadi Venus). Saya akan menyajikan situasi yang disederhanakan (hanya untuk membuat geometri lebih sederhana dan konsep utama lebih mudah dilihat), di mana planet dan bintang disejajarkan, jadi dari sudut pandang pengamat di khatulistiwa, sebuah planet yang lewat akan melewati garis khatulistiwa bintang. Di atas dalam ara. 6 menunjukkan tampilan samping; perhatikan garis merah dari ekuator planet yang mengamati ke bintang melalui ekuator planet yang melewati piringan bintang.

Dalam kasus penyelarasan sempurna, pengamat di ekuator planet luar akan melihat bagaimana planet bagian dalam melewati ekuator bintang. Ini ditampilkan sebagai garis merah di bagian bawah ara. 6. Tetapi pengamat dari kutub selatan planet luar akan melihat bagaimana planet bagian dalam melewati bintang di sepanjang jalur (garis ungu) di utara khatulistiwa bintang (dalam kasus kutub utara, semuanya akan menjadi sebaliknya). Jika kita mengukur sudut α di langit di antara lintasan di mana sebuah planet yang lewat bergerak dan mengetahui jari-jari R dari planet yang mengamati, kita dapat menggambar segitiga siku-siku yang menghubungkan planet yang lewat, pusat planet yang mengamati dan kutub dari planet yang mengamati, dengan sudut kecil? Trigonometri sederhana akan memberi kita jarak D antara planet-planet selama perjalanan, di mana

$$

$$D = R / tan \; \ alpha$$

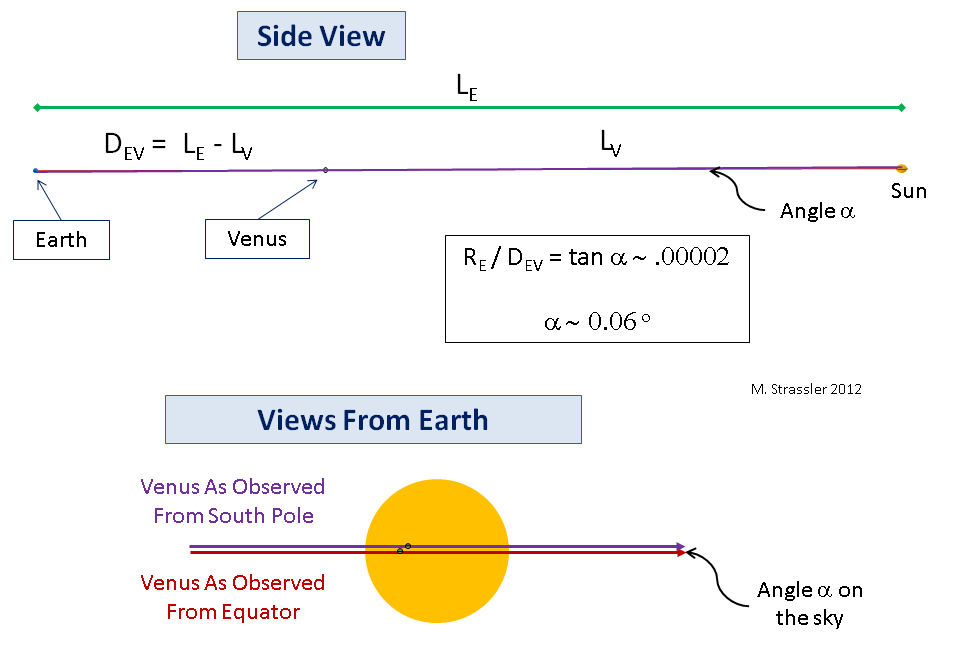Fig. 7

Hal yang sama berlaku untuk Bumi, Venus dan Matahari, kecuali bahwa Bumi dan Venus sangat kecil dibandingkan dengan jarak antara mereka dan Matahari sehingga sudut α akan sama dengan sekitar 1/20 °! (Ini adalah jumlah yang agak kecil, tetapi cukup terukur, meskipun pengukuran yang tepat dari jarak ke Matahari, yang ingin diperoleh para astronom abad ke-18, akan membutuhkan pengukuran yang akurat secara teknis agak rumit dari besarnya sudut kecil). Saya tidak akan menggambar sudut yang begitu kecil, jadi Anda harus mengambil kata saya untuk itu bahwa apa yang terjadi adalah versi dari apa yang saya gambarkan dalam gambar. 6, dengan planet dan bintang (Matahari) jauh lebih kecil dari yang dicat di sana, sehubungan dengan jarak. Bahkan gambar dalam gambar. 7 membuat planet lebih besar dari mereka. Tetapi idenya tetap tidak berubah: jarak D _EV antara Bumi dan Venus selama perjalanan dapat ditentukan dengan mengukur sudut paralaks α (bagian bawah Gambar 7; perhatikan bahwa diameter sudut Matahari sekitar 1/2 °).

Namun, masih ada banyak pertanyaan:

• Saya mengatakan bagaimana mengukur D _EV , jarak dari Bumi ke Venus selama perjalanan. Tapi bukankah tujuan kita untuk mengukur L _E dan L _V , jarak dari Bumi ke Matahari dan dari Venus ke Matahari?
• Tidak ada yang pergi ke kutub selatan Bumi untuk mengamati jalannya Venus pada 1761 atau 1769.
• Saya mengasumsikan orbit Bumi, Venus, dan posisi Matahari yang selaras dengan sempurna, sehingga dari titik di ekuator Bumi orang dapat melihat Venus bergerak di sepanjang ekuator Matahari. Tapi ini sebenarnya bukan masalahnya, dan bahkan tidak terlihat seperti penelusuran biasa (dan pada 2012 ini juga tidak).
• Sudut α cukup kecil untuk diukur secara akurat - terutama pada hari-hari sebelum fotografi dan pengiriman pesan instan, tanpa adanya indikasi yang jelas tentang lokasi kutub utara Matahari, yang membuatnya sulit untuk secara akurat membandingkan pengukuran jalur Venus yang dibuat dari dua titik berbeda di Bumi. Namun, tujuan utama adalah untuk mengukur sudut tidak lebih buruk dari 1 bagian dari 500 (0,2%) (meskipun karena efek drop hitam, hasilnya lebih dekat dengan 1 bagian dari 50 (2%)).

Bagaimana cara mengatasi masalah ini?

Pertama, bagaimana Anda beralih dari mengukur D _EV ke mengukur nilai yang diinginkan, L _E dan L _V ? Sederhana - kita sudah tahu semua hubungan, khususnya, kita sudah tahu L _E / L _V (kira-kira, dari Gambar 4, atau, jika kita mendekati masalah ini dengan lebih hati-hati, kita dapat menghitung dan lebih tepatnya) dari sudut maksimum betweenmax antara Venus dan Matahari dari sudut pandang Bumi. Kita juga tahu D _EV = L _E - L _V = L _E (1 - L _V / L _E ) dari Fig. 7. Oleh karena itu, kita dapat memperoleh nilai perkiraan L _E menggunakan:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \; α / (1 - sin \; \ gamma_ {max})$$

di mana α adalah sudut paralaks yang diukur selama transit, dan γ _maks adalah sudut maksimum antara Venus dan Matahari (Gbr. 5). Pengukuran yang lebih akurat membutuhkan geometri yang lebih kompleks, tetapi dengan ide dasar yang sama.

Kedua, bahkan jika orbit planet-planet itu sejajar sempurna, dua dimensi dari jalur Venus tidak perlu diukur dari ekuator dan kutub bumi. Mereka dapat diukur dari dua garis lintang. Geometri menjadi sedikit lebih rumit, tetapi tidak banyak, tetapi prinsipnya tetap (lihat Gambar 8).


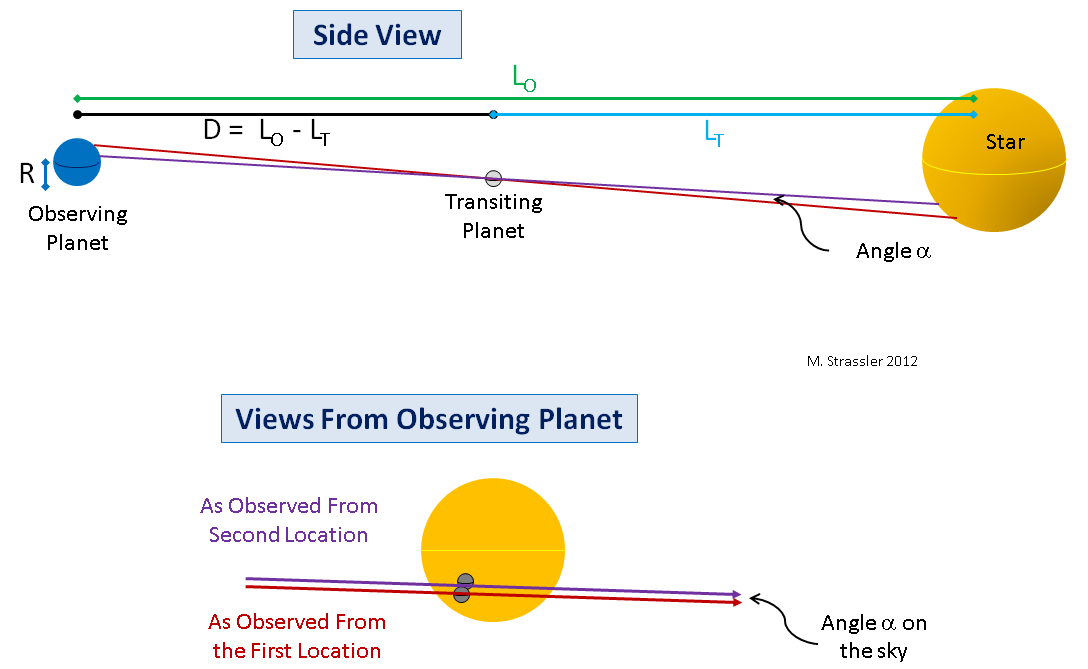Fig. 8

Ketiga, bahkan tanpa penyelarasan sempurna, sudut paralaks kecil akan muncul saat mengukur nilai dari dua titik Bumi yang berbeda, dan jika sudut ini diukur dengan baik, pengukuran ini dapat diubah (melalui persamaan yang sedikit lebih rumit) menjadi pengukuran D. Ini ditunjukkan pada Gambar. 8, turun.

Pertanyaan keempat adalah masalah historis yang kompleks dalam mengukur pergeseran sudut dari jalur Venus sambil melewati sudut α membawa kita pada upaya alternatif untuk mengukur waktu - baik waktu perjalanan, atau hanya awal dan akhir dari bagian, dan bukan sudut. Opsi pertama diusulkan oleh Halley berdasarkan ide Gregory, dan yang kedua, sebagai perbaikan lebih lanjut, diusulkan oleh Joseph Nicola Delille . Metode Halley tidak memerlukan sinkronisasi jam di berbagai tempat di Bumi; Metode Delil diperlukan, oleh karena itu, didasarkan pada teknologi arloji yang lebih maju.

Bahkan di abad XVII atau XVIII jauh lebih mudah untuk mengukur interval secara akurat, atau saat-saat awal dan akhir gerhana, daripada mengukur secara akurat lokasi Venus relatif terhadap piringan Matahari, terutama jika tidak ada foto. Dalam gbr. Gambar 9 menunjukkan bahwa jalur ungu dan merah dari Venus yang melintasi Matahari memiliki panjang yang sedikit berbeda karena mereka tidak melintasinya di satu tempat, yang berarti bahwa durasi lintasan akan berbeda dengan waktu yang terkait dengan sudut paralaks. Sayangnya, semuanya ternyata lebih rumit daripada yang terlihat pada pandangan pertama - Bumi berputar dan bergerak mengelilingi Matahari, sehingga pengamat menempuh jarak yang cukup besar selama perjalanan Venus melalui cakram Matahari. Oleh karena itu, banyak upaya diperlukan (perhitungan cukup rumit, meskipun dengan komputer modern mereka jauh lebih sederhana) untuk menentukan perbedaan interval waktu awal dan akhir bagian yang diamati oleh dua pengamat yang berbeda di Bumi, tergantung pada jarak ke Matahari.

Halley pada awal abad ke-18 memahami semua prinsip geometris yang diperlukan (jika Anda mengurangi frasa dan gaya bahasa Inggris yang ketinggalan zaman dari teks-teksnya, Anda akan terkejut melihat betapa modernnya pernyataan rumitnya terdengar, dan Anda akan melihat bahwa para ilmuwan tiga ratus tahun yang lalu sangat mirip dengan para ilmuwan saat ini, memiliki kecerdasan yang sama dan tidak memiliki teknologi ilmiah saat ini).


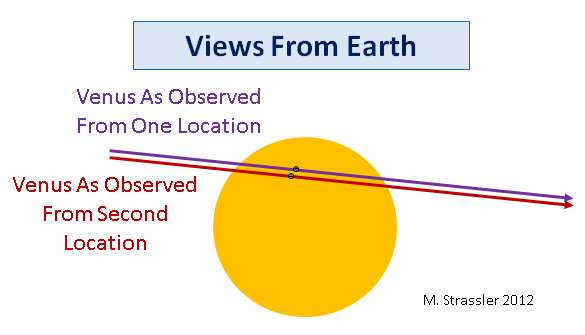Fig. 9

Semua ini menunjukkan bahwa paralaks - perbedaan dalam posisi yang tampak yang dikaitkan dengan Venus sehubungan dengan Matahari dari sudut pandang pengamat yang mengukurnya pada waktu yang sama tetapi dari tempat yang berbeda di Bumi - secara historis menjadi metode yang sangat penting dimana ditentukan ukuran tata surya. Hari ini, metode yang lebih kuat tersedia bagi kami, tetapi Anda mungkin tertarik pada kenyataan bahwa apa yang Anda lihat hari ini di langit adalah sangat penting secara historis, atau Anda hanya dapat menikmati pemandangan Venus, dengan anggun bergerak mengelilingi bintang kita.