
Jadi, Anda seorang programmer. Mengapa Anda membutuhkan polinomial? Sebagai contoh, maka, bahwa itu adalah tanah liat geometris yang baik, dari mana Anda dapat mencetak hal-hal yang berbeda.
Dari
artikel kami yang menjelaskan esensi analisis matematis menggunakan python, darah, dan dinamit sebagai contoh, dapat dilihat bahwa Anda dapat menganalisis dan mensintesis fungsi sewenang-wenang sebagai polinomial. Namun, tidak perlu bekerja secara khusus dengan fungsi. Terkadang Anda mungkin perlu memodelkan spline dari beberapa titik atau properti, seperti garis singgung kurva. Misalnya, Anda perlu membuat semacam animasi, atau efek video yang bagus, atau menggambar kurva melewati titik-titik tertentu, atau membuat permukaan yang rata di satu tempat dan melengkung di tempat lain.
Polinomial, termasuk yang spline, mungkin tidak selalu menjadi alat terbaik untuk tugas ini, tetapi mereka memiliki beberapa fitur yang sangat dihargai oleh programmer. Mereka sederhana dan serbaguna, dan, yang paling penting, sangat efektif dalam hal kinerja. Ambil contoh polinomial berikut:
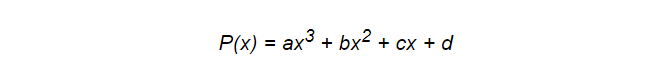
Untuk menghitungnya, hanya 6 tindakan perkalian dan 3 tambahan yang diperlukan. Ini penting karena model Anda akan secara konstan tunduk pada perhitungan. Tapi di sini kita bisa melakukan optimasi. Skema Horner akan membantu kita dengan ini. Dengan bantuannya, polinomial yang sama dapat ditulis sebagai

Dan ini hanya 3 perkalian dan 3 tambahan. Anda tahu, kami baru saja memulai, dan Anda telah belajar untuk menyingkirkan sepertiga dari perhitungan.
Interpolasi polinomial
Tugas mengadaptasi polinomial derajat
n ke
n +1 poin dalam ruang disebut interpolasi polinomial. Ada beberapa cara untuk mengimplementasikannya. Anda dapat menggunakan rumus interpolasi
Newton atau
Lagrange , tetapi cara termudah untuk mendapatkan polinomial interpolasi adalah dengan menyelesaikan sistem persamaan linear.
Jika polinomial melewati suatu titik, maka kita jelas dapat mengatakan bahwa
P (xi) = yi . Misalkan kita ingin mengadaptasi polinomial dengan seperangkat tiga poin. Ini berarti:

Dalam kasus umum, kita tidak dapat menarik garis melalui tiga titik arbitrer. Jadi kita harus menekuknya, membentuk parabola. Atau, dengan kata lain, perkenalkan polinomial tingkat kedua, juga dikenal sebagai fungsi kuadratik.

Karena xs dan ys diketahui, kita hanya perlu menyelesaikan sistem dan mencari tahu koefisien a, b, c, dan karena sistem ini terdiri dari tiga persamaan dan tiga variabel, kita biasanya bisa mendapatkan satu solusi tunggal.
Untuk memastikan hal ini, coba gerakkan posisi tiga poin di grafik yang lebih rendah dan lihat apa yang terjadi.

Grafik ini juga sangat berguna untuk analisis mental sistem linear. Dalam kasus umum, tidak mungkin untuk mencocokkan garis lurus pada tiga titik, seperti halnya tidak mungkin untuk menemukan solusi untuk sistem persamaan n dengan n-1 variabel yang tidak diketahui. Tapi terkadang itu mungkin. Misalnya, dalam kasus di mana beberapa titik bertepatan atau semuanya secara sengaja terletak pada satu garis lurus.
Situasi sebaliknya bahkan lebih menarik. Kita dapat menarik jumlah parabola yang tak terbatas melalui dua poin yang diberikan. Semuanya sama-sama cocok sebagai solusi untuk masalah tersebut. Dan pada saat yang sama, kita tidak bisa mendapatkan solusi unik yang lebih baik untuk sistem n persamaan dan variabel n +1.
Tetapi bagaimana jika itu masih mungkin? Bagaimana jika kita dapat memperkenalkan beberapa kriteria tambahan untuk memilih opsi yang paling cocok?
Sintesis
Pertanyaan serupa membawa kita ke wilayah sintesis polinomial. Dalam kasus kami, ini adalah persilangan antara deret polinom dan interpolasi polinom. Dengan bantuan deret, kita dapat memodelkan fungsi berdasarkan turunannya di beberapa titik, dan dengan bantuan sintesis, kita dapat menggunakan titik dan turunan (dan bukan hanya mereka, tetapi lebih pada waktu lain itu).
Turunan dari suatu fungsi terkait erat dengan sifat-sifat geometris grafiknya. Derivatif pertama menentukan garis singgung dari kemiringan garis singgung, dan yang kedua menentukan kelengkungan.
Misalkan kita perlu mendefinisikan suatu fungsi yang melewati dua titik, mengetahui garis singgung di kedua titik tersebut. Dalam hal ini, kita dapat dengan mudah mensintesisnya sebagai polinomial.
Seperti sebelumnya, kita perlu menuliskan sistem persamaan. Sekarang kita membutuhkan empat kondisi, jadi kita harus memilih polinomial derajat 3, yaitu fungsi kubik.
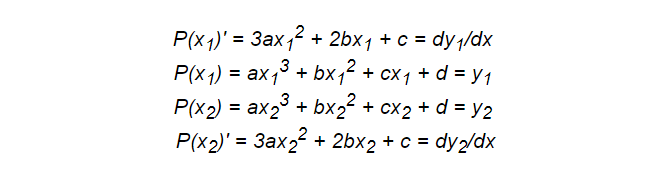
Beberapa persamaan didasarkan pada poin, sementara yang lain adalah turunan. Integral juga dapat ditambahkan di sini untuk memperkenalkan properti integer yang diperlukan, yang membuat teknik ini cukup efektif.
Tetapi kami akan terus mempertimbangkan fungsi yang menghubungkan dua titik garis halus kontinu dengan kendala tangensial pada titik-titik ini.


Fenomena runge
Interpolasi polinomial memiliki sifat tidak menyenangkan, yang memanifestasikan dirinya dalam peningkatan pertumbuhan osilasi pada kedua ujung interval dengan peningkatan jumlah titik. Fenomena ini disebut fenomena Runge. Ini membatasi kemungkinan menggunakan interpolasi polinomial sederhana.
Kelemahan lain dari pendekatan ini adalah sifat globalnya, yaitu, perubahan dalam seluruh fungsi bersama dengan sedikit perubahan pada posisi setidaknya satu poin. Dalam kombinasi dengan osilasi, hasilnya adalah kekacauan.

Node Chebyshev
Salah satu cara untuk memerangi kekacauan adalah dengan memilih mesh khusus untuk interpolasi -
node Chebyshev . Ini adalah nilai-nilai x khusus yang diperoleh dengan membagi setengah lingkaran dengan jari-jari 1 menjadi fragmen yang sama dan memproyeksikannya ke sumbu x.
Secara umum, sihir matematika tertentu tersembunyi dalam teknik ini, tetapi dari sudut pandang pragmatis, itu dimaksudkan untuk meminimalkan fenomena Runge. Dan meskipun tidak memungkinkan interpolasi benar-benar dapat diprediksi, semuanya berjalan stabil pada interval (-1: 1).

Tentu saja, Anda dapat memperpanjang interval sepanjang sumbu X sebanyak yang Anda butuhkan menggunakan transformasi affine satu dimensi. Tidak perlu mematuhi segmen
(-1; 1) .
Tetapi interpolasi pada saat yang sama tetap mempertahankan keberadaannya di mana-mana. Mengubah titik pertama masih mempengaruhi pengoperasian fungsi di dekat yang terakhir, meskipun tidak begitu signifikan.
Splines
Ada beberapa jenis splines, tetapi semuanya disatukan oleh satu skenario aplikasi. Segera setelah interpolasi global karena beberapa alasan tidak lagi sesuai dengan tugas kami, kami dapat membagi interval kami menjadi fragmen yang lebih kecil dan menetapkan fungsi terpisah untuk interpolasi pada masing-masingnya.
Satu-satunya hal yang perlu kita pertimbangkan adalah perlunya menghubungkan mereka di ujung untuk menjaga kontinuitas. Jika kami menjamin kontinuitas tidak hanya fungsi final, yang ditentukan secara terpisah, tetapi juga turunan pertamanya, maka dalam hal ini garis singgung dari masing-masing segmen akan bertepatan, dan jadwalnya akan terlihat mulus.
Ada
klasifikasi splines tertentu. Misalnya, ambil spine polinomial yang terdiri dari dua fragmen. Jika setiap fragmen ditentukan oleh polinomial tingkat ketiga, maka itu disebut kubik. Ini mungkin memiliki, misalnya, properti seperti kelanjutan turunan pertama, karena garis singgung di persimpangan fragmen bertepatan. Fragmennya tidak sama lebar. Ini bukan asal alami, karena kita dapat mengendalikan turunan pada akhirnya. Dan tentu saja, ini adalah interpolasi spline, karena ia melewati titik kisi yang telah kami tunjukkan.

Kesimpulan
Kemungkinan bahwa Anda harus mempraktikkan interpolasi Anda sendiri sangat kecil. Ada banyak solusi yang sudah jadi dan dalam banyak kasus Anda hanya perlu memilih alat yang tepat untuk pekerjaan itu. Bidang pengetahuan ini tidak begitu rumit, tetapi jumlah kata dan nama yang tidak diketahui dapat mendorong menjauh.
Tujuan dari panduan ini adalah untuk memberi Anda pemahaman dasar tentang ide-ide yang digunakan untuk bekerja dengan polinomial dan spline. Dalam kasus apa pun ia tidak berpura-pura menjadi lengkap, karena pada kenyataannya, seluruh buku ditulis pada masing-masing bab kecil dari bahan ini. Tetapi kami berharap, setidaknya, bahwa pendekatan interaktif untuk presentasi dalam materi ini akan bermanfaat tidak hanya untuk pengantar singkat, tetapi jika kebutuhan seperti itu muncul, itu akan membantu Anda menguasai topik yang lebih maju.
