Kosmologi - Stanford. Abstrak. Kuliah 1

Artikel ini membuka serangkaian catatan kuliah tentang Stanford University Cosmology. Kuliah sendiri dalam bahasa Inggris tersedia di: Kosmologi (2013) - Leonard Susskind - Stanford University . Saya menonton video ceramah dan menguraikan dengan senang hati. Dosen Leonard Susskind menjelaskan sangat mudah diakses dan menyenangkan. Jelaslah bahwa dia adalah orang yang berbakat dan guru yang sangat baik.

Universitas Stanford juga terkenal karena rekan senegaranya yang luar biasa, Andrei Linde, bekerja di sana, yang mungkin akan segera dianugerahi Hadiah Nobel dalam bidang fisika untuk kontribusinya pada kosmologi modern. Siapa peduli, saya sarankan Anda untuk menonton kuliahnya di The Many Faces of the Universe .

Sinopsis ini adalah usaha saya untuk belajar mandiri. Saya masih akan menulisnya sendiri di buku catatan. Tetapi saya memutuskan untuk menggabungkan bisnis dengan kesenangan. Saya harap ini juga menarik bagi seseorang.

Segera buat reservasi agar saya mencoba mencatat dekat dengan teks aslinya. Namun, di beberapa tempat saya membiarkan diri saya menambah atau menggeneralisasikan pernyataan dosen berdasarkan pengalaman saya sendiri sebagai ahli fisika spesialis. Ini dilakukan semata-mata untuk memfasilitasi pemahaman, pemahaman dan asimilasi materi.

Pada artikel ini, sinopsis kuliah 1 ditawarkan untuk Anda perhatikan, mungkin sekuelnya akan muncul nanti.

Ulasan sejarah

Kosmologi adalah subjek yang sangat kuno. Sejarah kosmologi berawal ribuan tahun yang lalu. Secara khusus, orang Yunani kuno tahu tentang kosmologi untuk waktu yang sangat lama.

Ceramah-ceramah ini mencakup periode waktu tidak lebih jauh dari paruh kedua abad kedua puluh, ketika Edwin Hubble menemukan hukum ekspansi alam semesta.

Jika kita berbicara tentang kosmologi sebagai ilmu, maka ini adalah bidang pengetahuan yang cukup baru. Kosmologi modern berasal dari penemuan radiasi peninggalan gelombang mikro dan perumusan teori big bang . Dan ini hanya terjadi pada 1960-an.

Hingga saat ini, kosmologi bukanlah cabang ilmu fisika, tetapi milik ilmu pengetahuan alam. Yaitu, dalam kosmologi pendekatan fenomenologis yang berlaku: observasi, pengukuran, klasifikasi, katalogisasi, dll.

Pada saat itu, akurasi pengukuran rendah. Dan karena itu tidak mungkin untuk merumuskan pernyataan yang tepat. Ada persamaan, tetapi tidak benar dan tidak akurat. Fisikawan selalu terlibat dalam proses penelitian, karena bintang, galaksi, dan benda langit lainnya memiliki karakteristik fisik seperti momentum sudut, misalnya. Ahli kimia fisik juga terlibat, karena benda langit memiliki komposisi kimia.

Namun, sikap terhadap Alam Semesta itu sendiri sebagai objek fisik, Alam Semesta sebagai sistem yang harus dipelajari secara matematis menggunakan seperangkat prinsip fisik dan persamaan yang tepat tepat terkait - ini adalah pendekatan yang relatif muda.

Properti Alam Semesta

Dalam kuliah ini, Semesta dianggap sebagai sistem fisik. Dan kita akan mempelajarinya menggunakan persamaan. Kita dapat memulai eksplorasi alam semesta dengan beberapa pengamatan umum.

Isotropi

Jadi, pengamatan pertama, yang, secara umum, mungkin tidak sepenuhnya akurat, seperti halnya semua fisika tidak sepenuhnya akurat, adalah bahwa Semesta adalah isotropik .

Isotropi berarti bahwa alam semesta terlihat sama ke segala arah. Tentu saja, ini hanya berlaku untuk jarak yang cukup jauh. Jika Anda melihat terlalu dekat, maka isotropi mungkin tidak teramati karena inhomogeneities lokal, misalnya, karena bentuk galaksi kita.

Keseragaman

Jika Semesta adalah isotropik, maka dapat diperdebatkan dengan sangat pasti bahwa Semesta juga harus homogen . Homogenitas tidak berarti keseragaman di setiap arah, tetapi di setiap tempat. Artinya, dalam skala besar, Semesta terlihat sama terlepas di mana pengamat berada - di galaksi kita atau di galaksi lain, yang jauh, jauh dari kita.

Galaksi

Galaksi pada skala Semesta adalah titik konsentrasi massa yang efektif. Kita bisa memperlakukan mereka sebagai poin materi. Perkiraan jumlah galaksi di bagian alam semesta yang terlihat adalah seratus miliar $$$10 ^ {11} = 100 \, 000 \, 000 \, $ 00$ . Pada gilirannya, setiap galaksi juga mengandung kira-kira $$$10 ^ {11}$ seratus miliar bintang. Kita harus ingat bahwa ini adalah jumlah galaksi hanya di dalam bola yang bisa kita lihat. Sejauh astronom dapat melihat dengan teleskop. Yaitu, yang terjauh yang bisa kita lihat adalah pada jarak dari tempat cahaya berhasil mencapai kita sepanjang seluruh keberadaan Semesta: sekitar 13 miliar tahun.

Fakta yang menarik. Jumlah total bintang di bagian alam semesta yang terlihat $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ , dan jika setiap bintang memiliki rata-rata 10 planet, maka ternyata $$$10 ^ {23}$ - Jumlah planet Avogadro di alam semesta. Mol substansi planet! (dosen tertawa)

Argumen melawan homogenitas alam semesta. Bantahan

Pertimbangkan sepotong jagat raya di mana kita berada. Kita tahu pasti, karena kita melihat bahwa Semesta adalah isotropik . Kami berasumsi bahwa alam semesta juga homogen . Tetapi apa yang akan terjadi jika alam semesta tidak homogen?

Jika Semesta adalah isotropik, maka satu-satunya cara agar tidak bersifat homogen adalah dengan memiliki struktur dalam bentuk sejenis kerang.


Hipotesa tentang alam semesta yang heterogen. Di sebelah kiri adalah Semesta homogen isotropik, di sebelah kanan adalah Semesta isotropis bukan Semesta homogen. Salib di tengah menunjukkan kita.

Jika demikian, maka pada titik lain mana pun Semesta tidak akan terlihat isotropik. Yaitu, jika kita tidak ingin percaya bahwa bagaimanapun kita berada tepat di pusat Semesta, dan agar seluruh Semesta memiliki simetri bola di sekitar kita, maka kita harus mengakui bahwa Semesta tidak hanya isotropik, tetapi juga homogen.

Prinsip kosmologis

Jadi, jika kita tidak percaya bahwa kita berada tepat di pusat Semesta, maka Semesta pasti homogen. Semesta yang homogen berarti bahwa Semesta diisi secara seragam dengan partikel (galaksi) di seluruh volume. Ini disebut prinsip kosmologis . Prinsip kosmologis itu benar, karena pengamatan kami menunjukkan hal ini, tentu saja, pada tingkat perkiraan tertentu.

Beberapa astronom mengklaim bahwa mereka mengamati heterogenitas skala besar di alam semesta. Dosen meragukan keandalan sumber dan pernyataan ini.

Tentu saja, gagasan tentang homogenitas alam semesta tidak sepenuhnya akurat. Bahkan fakta bahwa galaksi ada sudah menunjukkan bahwa ada heterogenitas. Ngomong-ngomong, tidak hanya ada galaksi tetapi juga kelompok galaksi. Namun, dalam skala yang cukup besar, kira-kira dari urutan 1 miliar tahun cahaya, Semesta terlihat homogen.

Pada awalnya, prinsip kosmologis hanyalah dalil. Tetapi dengan akumulasi data pengamatan, itu dikonfirmasi lebih dan lebih andal, dan pada akhirnya, radiasi gelombang mikro ditemukan, yang menunjukkan bahwa distribusi awal materi di alam semesta sangat homogen.

Pernyataan masalah fisik

Ada gas seragam dari partikel galaksi. Dan setiap galaksi berinteraksi dengan galaksi lain. Galaksi secara keseluruhan netral secara listrik. Tetapi mereka tidak netral secara gravitasi. Mereka berinteraksi melalui gravitasi Newton. Dan ini adalah satu-satunya kekuatan penting dalam skala besar. Gravitasi bekerja pada galaksi dan mencoba untuk menyatukannya.

Jadi, jika Anda melihat suatu titik di Semesta dan bertanya-tanya di mana ia harus bergerak, Anda dapat menebak bahwa dari semua sisi itu dikelilingi oleh jumlah massa yang sama. Mengikuti logika ini, dapat diasumsikan bahwa tidak ada galaksi yang bergerak sama sekali, dan Semesta harus statis, karena hasil gaya yang bekerja pada titik mana pun di Semesta adalah nol. Ini benar-benar salah!

Dan sekarang kita mendapatkan persamaan gerak Newton untuk alam semesta. Anda mungkin pernah mendengar bahwa alam semesta yang mengembang ini sesuai dengan teori relativitas umum Einstein, dan bahwa sebelum teori relativitas umum, hukum alam semesta yang mengembang tidak dapat dipahami. Ini tidak benar. Mungkin ini sangat historis. Tapi ini hanya fakta sejarah tentang tanggal, bukan tentang logika. Newton bisa mendapatkan persamaan dari alam semesta yang mengembang. Dan sekarang kita akan melakukannya seperti yang seharusnya dilakukan oleh Newton.

Sistem koordinat

Dalam masalah fisik apa pun, hal pertama yang harus dilakukan adalah memperkenalkan sistem koordinat. Alih-alih memilih langkah kisi sebagai jarak: 1 meter, sejuta kilometer, seribu tahun cahaya, kita akan memilih kisi sehingga simpulnya melekat erat pada galaksi. Karena alam semesta homogen, kita dapat melakukannya. Kemudian galaksi akan selalu tetap pada koordinat yang kira-kira sama, terlepas dari apa yang terjadi pada alam semesta. Artinya, galaksi tampaknya "beku" ke dalam kisi koordinat.

Sama sekali tidak jelas bahwa ini bisa dilakukan. Jika galaksi bergerak sepenuhnya secara tidak sengaja dan ke arah yang sama sekali berbeda, maka kita tidak bisa melakukan ini. Tetapi kita melihat bahwa galaksi bergerak secara kebetulan. Kita melihat bahwa galaksi bergerak bersama, persis seolah-olah mereka tertanam dalam kotak koordinat tertentu. Dan apa yang kita lihat memungkinkan kita melakukan ini, karena kecepatan galaksi relatif satu sama lain konsisten dan tidak disengaja.

Kami memperkenalkan kotak $$$(x, y, z)$ . Koordinat ini tidak diukur dalam satuan panjang. Jika kita menganggap dua galaksi dipisahkan oleh suatu interval $$$\ Delta x$ lalu jaraknya $$$D$ di antara mereka (dalam meter) dinyatakan sebagai

$$

$$D = a \, \ Delta x$$

dimana $$$a$ Apakah parameter skala, yang mungkin konstan, tetapi secara umum, mungkin tidak. Parameter skala mungkin tergantung waktu. $$$a = a (t)$ .

Dengan demikian, oleh teorema Pythagoras, jarak antara dua galaksi umumnya ditulis sebagai

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

Dan tentu saja, parameternya $$$a$ bukan konstanta. Jika itu adalah konstanta, maka galaksi akan menjadi statis, mereka tidak akan bergerak ke mana pun. Dan ini bukan yang kita amati. Kami melihat bahwa mereka terbang terpisah.

Hukum Hubble

Kami menulis kecepatan relatif antara dua galaksi. Kami membedakan rumus sebelumnya dalam waktu. Kami memperhitungkannya $$$\ Delta x$ - Ini adalah interval tetap, yang tidak dapat diubah sesuai dengan kondisi untuk membangun sistem koordinat. Lalu

$$

$$\ mathcal {V} = \ dot {a} \, \ Delta x$$

tempat kami menggunakan notasi $$$\ dot {a} = da / dt$ .

Kami sekarang menulis rasio kecepatan relatif dua galaksi dengan jarak di antara mereka

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ dot {a} (t)} {a (t)}$$

Catat itu $$$\ Delta x$ berkurang, dan rasio ini tidak bergantung pada koordinat sama sekali. Artinya, rumus ini berlaku untuk dua galaksi, tidak peduli seberapa jauh atau dekat mereka.

Relasi ini disebut parameter konstanta Hubble.

$$

$$H (t) = \ frac {\ dot {a} (t)} {a (t)}$$

dan itu tidak tergantung pada koordinat. Kemudian Anda dapat menulis yang sama dalam bentuk standar

$$

$$\ mathcal {V} = H \, D$$

Kecepatan relatif dua galaksi sebanding dengan jarak di antara mereka.

Anda perlu memahami bahwa kami tidak akan pernah menuliskannya jika Hubble tidak menemukan hukumnya. Hukum Hubble, di sisi lain, tidak begitu mengejutkan. Ada pepatah: "Tidak mengherankan bahwa kuda tercepat mengendarai di depan semua orang." Semakin cepat Anda bergerak, semakin jauh Anda. Dan ini adalah fakta yang ditemukan Hubble.

Massa materi di alam semesta

Pertimbangkan beberapa volume $$$\ Delta x \, \ Delta y \, \ Delta z$ . Kami mengajukan pertanyaan: massa apa yang terkonsentrasi dalam volume ini? Biarkan $$$\ nu$ Apakah massa suatu zat dalam volume elementer $$$dx \, dy \, dz$ (dalam kilogram). Kemudian massa dalam volume $$$\ Delta x \, \ Delta y \, \ Delta z$ sama dengan

$$

$$M = \ nu \, \ Delta x \, \ Delta y \, \ Delta z$$

Berapa volume metrik area ini? Sejak $$$D = a \, \ Delta x$ kita bisa menulis

$$

$$V = a ^ 3 \, \ Delta x \, \ Delta y \, \ Delta z$$

Berapa kepadatan bahan di area ini? Menurut definisi, kepadatannya adalah $$$\ rho = M / V$ , yaitu, dengan mempertimbangkan dua formula sebelumnya, kami memperoleh

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

Ini adalah kepadatan fisik standar suatu bahan.

Meskipun jumlah total massa dalam volume $$$\ Delta x \, \ Delta y \, \ Delta z$ tidak berubah, karena galaksi "beku" ke dalam kotak koordinat, kepadatan absolut materi dalam volume yang sama dapat berubah, karena parameter $$$a (t)$ tergantung waktu.

Teorema Newton

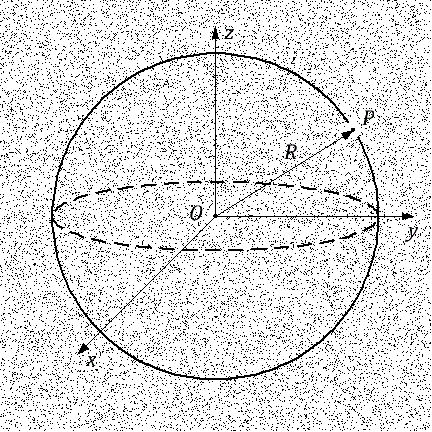Ilustrasi untuk teorema Newton

Pertimbangkan dua galactiti. Kami selalu dapat menempatkan salah satu dari mereka di tempat asalnya. Biarkan galaksi $$$O$ adalah asal, dan galaksi $$$P$ agak jauh darinya.

Teorema Newton menyatakan bahwa gaya gravitasi bekerja pada sebuah galaksi $$$P$ hanya bergantung pada jumlah massa di dalam bola yang berpusat di titik asal $$$O$ , dan melewati galaksi $$$P$ . Pernyataan kedua dari teorema Newton adalah bahwa seluruh massa di dalam bola ini dapat dianggap terkonsentrasi di pusat pada titik asal pada titik tersebut. $$$O$ , asalkan massa di dalam bola didistribusikan, jika tidak seragam, maka setidaknya secara isotropis .

Dengan kata lain, efek seluruh massa di dalam bola di galaksi $$$P$ setara dengan seolah-olah massa ini terkonsentrasi pada satu titik tunggal $$$O$ , yang merupakan pusat bola.

Persamaan gerak Newton

Temukan jarak antar galaksi $$$P$ dan $$$O$ . Galaksi $$$P$ memiliki koordinat $$$(x, y, z)$ yaitu jarak dari pusat ke galaksi $$$P$ sama dengan

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

Kami dapat memperkenalkan notasi

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ tidak diukur dalam meter, tetapi dalam satuan yang sama dengan $$$x$ , $$$y$ dan $$$z$ dan tidak tergantung waktu. Lalu

$$

$$D = a (t) \, R$$

Kami sekarang merekam kecepatan dan percepatan galaksi $$$P$

$$

$$\ mathcal {V} = \ dot {a} (t) \, R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \, R$$

Sekarang kita harus menyamakan akselerasi $$$\ mathcal {A}$ untuk akselerasi yang terkait dengan seluruh massa gravitasi di dalam bola jari-jari $$$R$ . Nyatakan massa galaksi $$$P$ untuk $$$m$ , dan massa semua materi di dalam bola di luar $$$M$ . Kemudian gaya gravitasi bekerja di galaksi $$$P$ sama dengan

$$

$$F = -G \ frac {m \, M} {D ^ 2}$$

dimana $$$G = 6.67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - Konstanta gravitasi. Tanda minus dalam rumus berarti bahwa itu adalah kekuatan yang menarik.

Sekarang Anda dapat merekam akselerasi galaksi $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

Kami menyamakan dua ekspresi untuk $$$\ mathcal {A}$ dan dapatkan

$$

$$\ ddot {a} (t) \, R = -G \ frac {M} {D ^ 2}$$

Kami memperhitungkannya $$$D = a \, R$ lalu

$$

$$\ ddot {a} \, R = - \ frac {M \, G} {a ^ 2 \, R ^ 2}$$

Bagi kedua belah pihak dengan $$$a \, R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \, G} {a ^ 3 \, R ^ 3}$$

Temukan volume bola

$$

$$V = \ frac {4} {3} \ pi \, D ^ 3 = \ frac {4} {3} \ pi \, a ^ 3 \, R ^ 3$$

Kami mengalikan pembilang dan penyebut sisi kanan dengan $$$4 \ pi / 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \, G \, \ rho$$

Persamaan ini tidak tergantung pada $$$R$ , dan memang benar untuk setiap galaksi di alam semesta. Persamaan ini adalah persamaan fundamental sentral dari kosmologi .

Salah satu konsekuensi dari persamaan ini adalah bahwa mustahil bagi Alam Semesta untuk statis jika tidak kosong. Dari persamaan ini dapat disimpulkan bahwa Semesta hanya bisa statis jika kosong.

Kita dapat menulis ulang persamaan ini, mengingat itu $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \, \ nu} {a ^ 3}$$

Persamaan ini pertama kali diperoleh dalam konteks teori relativitas umum oleh Alexander Friedman. Persamaan ini tidak memberi tahu kita apakah alam semesta mengembang atau menyusut. Ia hanya mengatakan bahwa turunan kedua dari faktor skala adalah negatif. Yaitu, jika Semesta mengembang, maka ia melambat, dan jika Semesta menyusut, maka ia berakselerasi.

Faktanya, alam semesta mengembang dan tidak melambat. Kami baru saja melakukan apa yang bisa dilakukan Newton dan semua kosmolog dianggap benar sampai sekitar tahun 1998. Model ini secara umum diterima dan disebut model standar Alam Semesta sampai percepatan perluasan Alam Semesta ditemukan secara terbuka. Sejauh ini, sisi kanan persamaan hanya memiliki satu istilah. Bahkan, harus ada beberapa istilah yang berkaitan dengan teori relativitas umum.

Kecepatan Keberangkatan

Sekarang tulis energi penuh galaksi $$$P$ sebagai jumlah dari kinetik dan potensi

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D}$$

Energi bisa positif atau negatif tergantung pada rasio antara kedua istilah ini. Penting juga untuk diingat bahwa total energi partikel $$$P$ disimpan. Jika energi total positif, maka partikel tidak dapat kembali. Partikel kembali hanya ketika energi total negatif. Batas kasus adalah total energi nol. Pecahkan persamaannya $$$E = 0$ untuk $$$\ mathcal {V}$ untuk menemukan kecepatan keberangkatan.

$$

$$\ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

Persis seperti galaksi $$$P$ seluruh Semesta dapat memiliki kecepatan lebih tinggi dari kecepatan keberangkatan, kurang dari kecepatan keberangkatan atau sama dengan kecepatan keberangkatan. Jika kecepatan Semesta lebih tinggi dari kecepatan keberangkatan, maka ia mengembang dan tidak pernah mulai menyusut, jika Semesta memiliki kecepatan di bawah kecepatan keberangkatan, maka cepat atau lambat ia akan mulai menyusut.

Tulis ulang persamaan energi total

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = E$$

Persamaan Friedman

Pertimbangkan kasus ketika kecepatan alam semesta bertepatan dengan kecepatan keberangkatan.

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = 0$$

Sederhanakan ungkapan: bagi dengan $$$m$ , kalikan dengan 2, bagi dengan $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ dot {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

Dalam istilah kedua, kita mengalikan pembilang dan penyebut dengan $$$4 \ pi / 3$ . Kemudian dalam penyebut kita mendapatkan volume metrik bola $$$V$ . Mengingat itu $$$M / V = ​​\ rho$ kita dapatkan

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} G $ rho$$

Ini disebut persamaan Friedman . Ini sama dengan persamaan Newton yang diperoleh di atas. Karena kita mengasumsikan bahwa energi total adalah nol, alam semesta seperti itu mengembang, secara asimptot melambat menjadi nol, tetapi tidak pernah melintasi nol dan tidak mulai menyusut.

Ingat sekarang $$$\ rho = \ nu / a ^ 3$ . Tulis ulang persamaan Friedman

$$

$$\ kiri (\ frac {\ dot {a}} {a} \ kanan) ^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

Parameter $$$\ nu$ sangat fleksibel.Itu sepenuhnya tergantung pada pilihan kita dari grid. Dan secara umum, kita bahkan bisa memilihnya$$$\frac{8\pi}{3}\nu G = 1$ . Lalu

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

Sisi kanan persamaan ini selalu positif, dan karenanya, laju ekspansi
$$˙ a tidak pernah menjadi sama dengan nol. Ingat sekarang$\dot{a}$$$˙ a /a=HadalahparameterkonstantaHubble. Ini juga mengikuti dari persamaan bahwa parameter Hubble tidak pernah berubah tanda. Namun, masih melambat. Parameter Hubble menjadi semakin sedikit seiring dengan waktu. Persamaan ini sangat penting untuk semua kosmologi. Cara sederhana untuk menyelesaikannya adalah dengan mencari solusi dari jenis tertentu, yaitu, kita akan mencari solusi dalam bentuk$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

dimana $$$c$ dan $$p adalah beberapa konstanta.$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

Kami telah mendapatkan solusi untuk persamaan Friedman.


Grafik solusi dari persamaan Friedman

Alam semesta yang sebenarnya mengikuti keputusan ini hanya sampai pada titik waktu tertentu, dan kemudian mulai berakselerasi. Newton bisa melakukan ini. Dia datang sangat dekat. Mengajukan semua pertanyaan yang tepat. Dosen yakin bahwa Newton, kemungkinan besar, melakukan ini dan menerima keputusan ini. Namun, informasi seperti itu tentang alam semesta bertentangan dengan pandangan agamanya, dan karena itu ia tidak mempublikasikan penemuannya.