Bisakah saya memenangkan judi? Simulasi Python

Hai Geektimes.

Dalam proses idle idle, muncul ide untuk mempelajari berbagai judi, pada saat yang sama untuk lebih memahami cara kerjanya. Hasilnya, meskipun secara umum jelas, cukup menarik untuk dibagikan kepada publik.



Kepada siapa detailnya menarik, saya bertanya di bawah kucing.

Dice: Craps Game

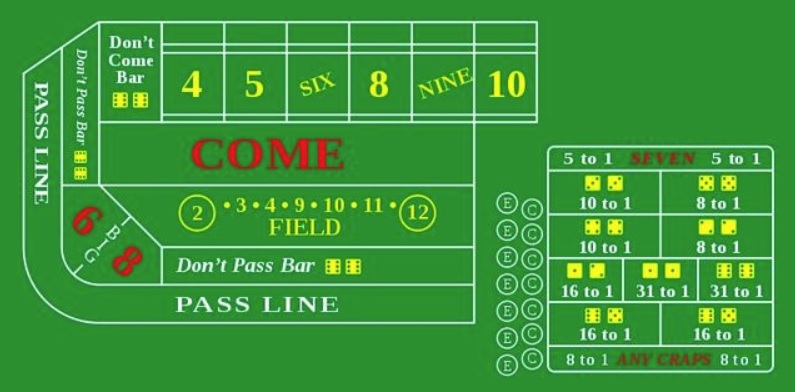
Kemungkinan besar, pilihan yang sederhana dan mudah dimengerti secara intuitif - ada sebuah kubus dengan tanda dari 1 hingga 6, dan probabilitas nomor tertentu yang keluar adalah 1/6. Tetapi bermain dengan cara ini akan membosankan, sehingga game dengan aturan yang lebih kompleks sangat populer. Game kebetulan yang populer adalah craps , gambar di atas menunjukkan gambar tabel game. Seperti yang Anda lihat, ada banyak segalanya, tetapi kami tidak akan membahas seluk beluk yang mendalam.

Setiap giliran permainan terdiri dari melemparkan dua dadu, akumulasi poin ditambahkan. Seperti yang dikatakan artikel itu , “Aturan mainnya langsung: pemain melempar dua dadu, dan jika jumlah poin pada mereka adalah 7 atau 11, ia menang, jika 2, 3 atau 12, ia kalah. Ketika jumlah yang berbeda jatuh pada dadu, penembak melempar mereka ke kombinasi menang atau kalah. "

Mari kita lihat seberapa banyak Anda bisa menang dengan cara ini. Tidak perlu pergi ke kasino untuk ini, kami akan menggunakan Python untuk mensimulasikan permainan. Kami menulis fungsi untuk sekali lemparan:

import random def shoot(): return random.randint(1,6) + random.randint(1,6) 

Kami akan menulis fungsi simulasi satu langkah sesuai dengan aturan di atas.

 def move(): while True: val = shoot() print "Dice roll:", val if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False 

Mari kita atur pemain virtual kita jumlah awal $ 100, dan memulai proses permainan. Biarkan pemain kami menghasilkan 100 taruhan, setiap kali 1u.e.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Kami memulai simulasi dari 100 pertandingan dan terkejut dengan hasilnya, pemain menang , dan dengan margin kemenangan yang nyata dari kekalahan: Menangkan 63, Kehilangan 37, Uang 126. Kami menambah jumlah pertandingan menjadi 1000 dan berlari lagi, pemain menang lagi: Menang 680, Kehilangan 320, Uang 460 .

Jelas bahwa ada sesuatu yang salah di sini - permainan di mana pemain akan selalu hitam, hampir tidak populer di kasino, itu hanya akan bangkrut. Mari kita coba mencari tahu.

Tampaknya secara intuitif bahwa ketika melempar dadu, probabilitas dari setiap aspek yang jatuh sama-sama memungkinkan. Dan ini benar, tetapi dalam kasus satu kubus. Jika ada dua kubus, maka semuanya menjadi lebih rumit. Sebagai contoh, angka 7 dapat drop out sebagai 3 + 4, 2 + 5, 1 + 6, tetapi angka 12 dapat jatuh hanya sebagai kombinasi 6 + 6.

Dalam buku catatan Jupyter kami menyusun jadwal untuk hilangnya jumlah dari 1 hingga 12 untuk 100 lemparan:

 from matplotlib import pyplot as plt %matplotlib inline y = [ shoot() for v in range(100) ] plt.hist(y) 

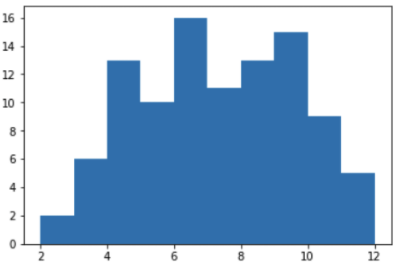
Asumsinya telah dikonfirmasi, dan jumlah dari pusat benar-benar semakin sering jatuh. Dengan demikian, angka 7 dan 11 benar-benar jatuh lebih sering daripada 2,3 atau 12. Dan kemungkinan mendapatkan kombinasi pemenang "7 atau 11" benar-benar lebih tinggi.

Bagaimana ini bisa terjadi? Sayangnya, jawabannya sederhana - penulis artikel yang dikutip di atas sama sekali tidak mengerti aturan permainan. Teks " aturan mainnya langsung: pemain melempar dua dadu, dan jika jumlah poin pada mereka adalah 7 atau 11, ia menang, jika 2, 3 atau 12 - ia kalah " sangat jauh dari kebenaran, dan aturan dalam craps tidak begitu langsung seperti yang terlihat .

Aturan sebenarnya untuk bertaruh pada pass line ternyata sedikit lebih rumit (ada jenis taruhan lain, mereka yang berharap bisa mengetahuinya sendiri).

Langkah 1 : Rol dibuat. Jika 7 atau 11 jatuh, pemain menang, jika 2, 3 atau 12, pemain kalah. Jika nomor lain jatuh, itu diingat di bawah titik nama.

Langkah 2 : Rol dibuat. Jika 7 jatuh, maka pemain kalah. Jika poin jatuh, maka pemain menang. Jika nomor lain jatuh, langkah itu diulangi (saat ini, pemain juga bisa bertaruh pada nomor lainnya).

Memang, semuanya sedikit lebih rumit daripada yang dijelaskan dalam versi aslinya. Kami menambahkan fungsi simulasi dengan mempertimbangkan aturan yang lebih tepat.

 def move(): point = 0 while True: val = shoot() if point == 0: # First move if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False point = val else: # 2..N move if val == 7: return False if val == point: return True 

Hasilnya sekarang lebih mirip dengan kebenaran: untuk 100 pertandingan, pemain menang 43 kali, kalah 57 kali, saldo di akhir pertandingan adalah 86.u. dari 100 yang asli. Menarik juga bahwa jumlah kemenangan ternyata cukup besar, dan hanya sedikit kurang dari 50%. Ini adalah strategi yang kompeten dari sudut pandang kasino - ini memungkinkan Anda untuk mempertahankan minat peserta dalam permainan (itu tidak menarik untuk kalah sepanjang waktu), tetapi pada saat yang sama, saldo laba kasino tetap positif, dan saldo uang pemain juga negatif.

Mari kita lihat lebih detail apa yang didapat untuk simulasi 100 game.
- Kesempatan untuk menang pada langkah pertama turun sekitar 20 kasus.
- Peluang untuk segera kalah pada langkah pertama jatuh dalam 15 kasus.
- Dalam 65 kasus yang tersisa, permainan berlanjut, dan semuanya rumit: pilihannya datang dari dua angka, 7 dan poin, tetapi seperti yang Anda lihat dari grafik di atas, kemungkinan terjatuhnya angka "kalah" nomor 7 adalah maksimum, yang secara umum harus dibuktikan.

Sangat menarik untuk dicatat bahwa peluang untuk menang di 45% agak tinggi. Jadi mungkinkah menang? Dalam jangka pendek, misalnya, dalam simulasi lain, pemain itu "beruntung", dan dalam 100 pertandingan ia menambah modal virtualnya dari 100 menjadi 112ye.



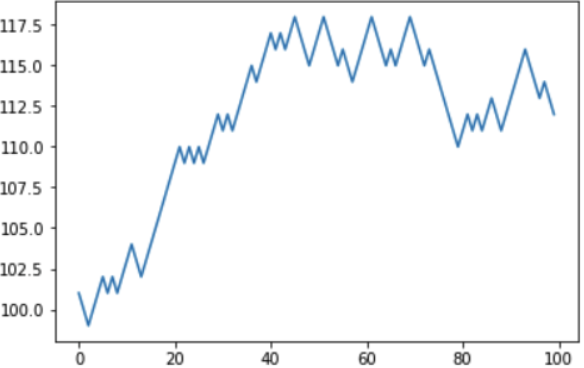
Tapi simulasi berikutnya sudah menunjukkan keseimbangan negatif: pemain mengurangi kondisinya dari 100 menjadi 88ye, setelah kehilangan, 12ye yang sama “menang” sebelumnya.

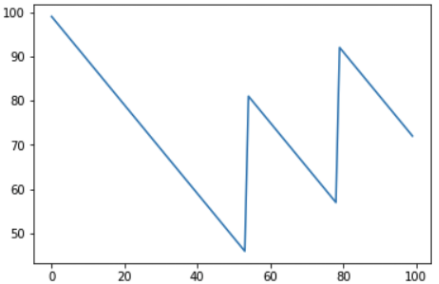
Jika Anda menambah jumlah iterasi menjadi 1000, Anda dapat melihat bagaimana keseimbangan moneter pemain dalam jangka panjang:



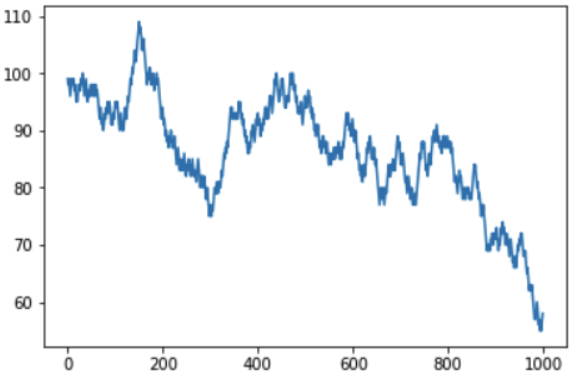
Jelas bahwa dengan peluang memenangkan setiap pertandingan kurang dari 50%, jumlah uang yang dihasilkan di akun pemain akan secara bertahap berkurang, dan jumlah keuntungan kasino akan meningkat secara bertahap. Pada grafik, semburan dan jatuh terlihat, dan pertanyaan yang wajar mungkin muncul - dapatkah mereka diprediksi? Sial, tidak, karena Gulungan dadu adalah peristiwa yang tidak terkait satu sama lain, dan hasil sebelumnya tidak memengaruhi yang berikut dengan cara apa pun. Anda dapat mengulangi ide utama sekali lagi - Anda bisa menang satu atau bahkan beberapa kali, tetapi dalam jangka panjang tidak mungkin untuk tetap di plus di kasino, aturan permainan disusun sehingga keseimbangan tidak menguntungkan pemain.

Ada jenis taruhan lain dalam permainan dadu, dan mereka yang ingin dapat menganalisanya sendiri.

Rolet Amerika

Jenis perjudian populer berikutnya adalah roulette, pertimbangkan versi Amerika-nya.



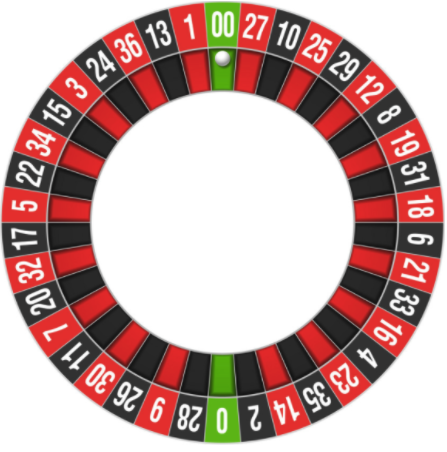
Lapangan bermain roulette dibagi menjadi 38 sel: 36 zona dengan angka + 2 zona "nol" dan "nol ganda". Sebuah bola yang dilemparkan ke roda roulette jelas akan berhenti di salah satu zona. Pemain dapat membuat berbagai taruhan, di mana ada lebih dari 10 jenis, pertimbangkan beberapa di antaranya.

Hitam-merah (atau bahkan aneh)

Seorang pemain menang jika taruhan yang dia sebutkan bertepatan. Jelas, probabilitas hitam atau merah akan menjadi 50/50, jika bukan karena dua bidang nol - jika mereka mengenai mereka, taruhan kalah. Seperti dalam kasus craps, ini membuat kemungkinan menang hanya sedikit di bawah 50% - tetapi "sedikit" ini cukup untuk berada di zona merah.

Kami akan menulis fungsi mensimulasikan langkah menggunakan angka acak dari 1 hingga 38, 2 digit terakhir akan dianggap sebagai "nol".

 def move_roulette1(): val = random.randint(1,38) if val == 37 or val == 38: return False return val % 2 != 0 

Jalankan simulasi untuk 100 game, kodenya sama seperti pada simulasi craps, kami hanya mengubah pemanggilan fungsi.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette1() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Hasil: dalam 100 upaya, pemain menang 46 kali dan kalah 54 kali. Grafik menunjukkan bahwa pemain memiliki "naik" dan "jatuh", tetapi keseimbangan terakhir masih negatif.



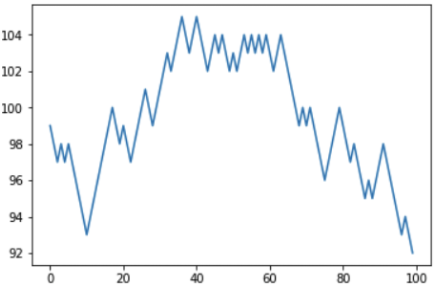
Semakin banyak kami bermain, semakin dalam kami pergi ke minus, dan kasino, masing-masing, menjadi plus:



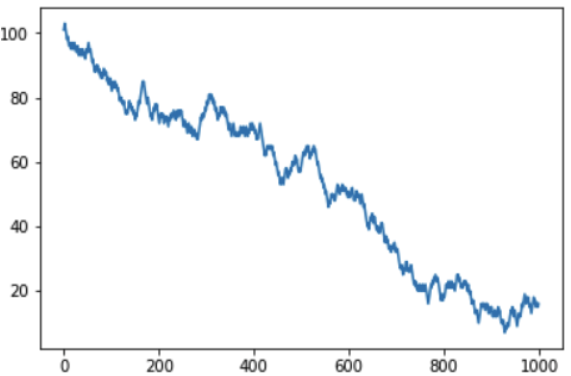
Ada pertanyaan dari pembaca mengapa saya tidak menganggap roulette Eropa dengan satu bidang "nol" - seperti yang Anda duga, peluang menang di sana benar-benar lebih tinggi, tetapi prinsip umum tidak berubah. Bahkan, perbedaannya hanya pada "kehilangan kecepatan". Berikut adalah jadwal bersama untuk versi Amerika dan Eropa dari permainan:


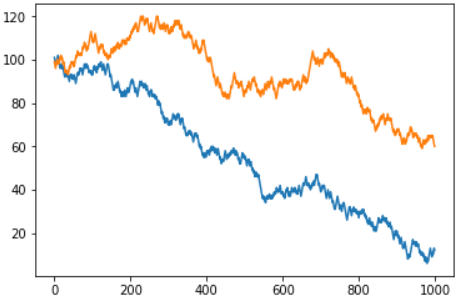
Mereka yang ingin menguji roulette versi Eropa dengan 37 slot dapat menggunakan opsi fungsi yang kedua:

 def move_roulette1(): val = random.randint(1,37) if val == 37: return False return val % 2 != 0 

Taruhan pada nomor tertentu

Pemain juga dapat bertaruh pada nomor tertentu, taruhan untuk menang adalah 35: 1. Tampaknya hebat, tetapi mudah untuk menebak bahwa kemungkinan nomor roulette yang keluar adalah 1:38, yaitu lagi, sedikit kurang.

Mari kita tambahkan fungsi taruhan ke nomor tertentu:

 def move_roulette2(num): val = random.randint(1,38) return val == num 

Simulasi, kami menganggap bahwa pemain memakai nomor 10:

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette2(10) if step is True: money_total += 35*bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Akibatnya, pemain menang 2 kali dan kalah 98 kali, saldo terakhir adalah -28.u.



Taruhan pada dua angka

Anda bisa bertaruh pada dua angka - peluang menang lebih tinggi, tetapi taruhannya lebih sedikit dan 17: 1.

Mari kita menulis fungsi:

 def move_roulette3(num1, num2): val = random.randint(1,38) return val == num1 or val == num2 

Untuk 100 upaya simulasi kami, pemain menang 3 kali dan kalah 97 kali, sisanya adalah -46u.e.

Ada jenis taruhan lain, misalnya, untuk 4 angka dengan koefisien 1: 8, mereka yang ingin dapat bereksperimen sendiri. Seperti yang Anda tebak, semua peluang dirancang sehingga pemain merah. Tampaknya menggoda untuk menempatkan 1ye pada angka untuk memenangkan sebanyak 35ue. Tetapi jumlah yang menang meningkat 35 kali, dan kesempatan menang berkurang 38 kali - saldo terakhir masih akan menguntungkan kasino.

Lotto 6 dari 45

Hal berikutnya yang menarik untuk diperiksa adalah lotre. Prinsip permainan ini cukup sederhana - ada 45 bola dalam drum, 6 di antaranya jatuh secara acak. Harga tiket menurut situs web Gosloto adalah 100 rubel, dan hadiah tergantung pada jumlah bola yang bisa ditebak. Perkiraan urutan kemenangan adalah sebagai berikut: 2 bola tebakan memberi kemenangan 100r, 3 bola tebakan memberi 300r, 4 bola - 3000r, 5 bola - 300.000r dan 6 bola - hadiah super sekitar 10.000.000r.

Pertama, tulis program untuk melempar bola dan membandingkan hasilnya:

 def lottery(values): balls = range(1, 45+1) b1 = balls.pop(random.randint(0, len(balls)-1)) b2 = balls.pop(random.randint(0, len(balls)-1)) b3 = balls.pop(random.randint(0, len(balls)-1)) b4 = balls.pop(random.randint(0, len(balls)-1)) b5 = balls.pop(random.randint(0, len(balls)-1)) b6 = balls.pop(random.randint(0, len(balls)-1)) s = [b1,b2,b3,b4,b5,b6] res = list(set(s) & set(values)) return len(res) 

Bola acak “mendapat” 6 kali dari susunan bola, maka jumlah elemen dari persimpangan dua set ditentukan. Sekarang kita akan membangun grafik dari total keuntungan pada jumlah tiket yang dibeli. Untuk mempermudah, kami menganggap bahwa pemain bertaruh pada nomor yang sama.

 money = [] money_total = 0 ticket_price = 100 for p in xrange(N): val = lottery([3,7,12,18,33,28]) if val == 2: money_total += 100 if val == 3: money_total += 300 if val == 4: money_total += 3000 if val == 5: money_total += 300000 if val == 6: money_total += 10000000 money.append(money_total) x = range(0, N) price = map(lambda x: ticket_price*x, x) from matplotlib import pyplot as plt %matplotlib inline plt.plot(price, money) 

Untuk memahami urutan besarnya: jika Anda membeli 100 tiket (jumlah total yang dihabiskan adalah 10.000r), maka ini menghasilkan 14 bola "ganda" dan satu "tiga". Total keuntungan adalah sekitar 2000r dengan 10.000r dihabiskan.

Jadwal pembayaran untuk jumlah yang dihabiskan hampir linier:



Ternyata jika Anda membeli tiket dalam sejuta, keuntungannya adalah 250 ribu. "Hadiah super" dalam simulasi tidak pernah rontok, meskipun secara teori, itu mungkin saja terjadi. Ngomong-ngomong, seperti yang tertulis dalam aturan, kumpulan hadiah adalah 50% dari tiket yang terjual, tetapi “hadiah super” tidak selalu rontok, sehingga seperti halnya kasino, penyelenggara, tentu saja, selalu menang.

Mesin slot

Mereka juga bekerja pada prinsip acak (semu), “pseudo” karena Kode di dalamnya sudah lama terprogram dan tidak memiliki mekanika bersih. Prinsip-prinsip umum yang dijelaskan di atas untuk mesin slot juga berfungsi, dan grafik kemungkinan besar tidak akan berbeda, mereka yang ingin dapat menambahkan fungsi simulasi sendiri.

Artikel bagus tentang desain mesin game sudah ada di Geektimes.

Kesimpulan

Mungkin artikel ini tidak membuka Amerika bagi banyak orang, tetapi pada grafik itu, pada prinsipnya, lebih visual. Ternyata menjadi lebih menarik untuk membandingkan pendekatan psikologis yang berbeda secara mendasar dengan permainan. Kemenangan dalam lotre berpotensi besar, tetapi sangat jarang. Di kasino, pendekatannya adalah sebaliknya - taruhan diatur sehingga seseorang akan menang sesering mungkin. Dengan syarat, setelah membuat 10 pertandingan di kasino, seseorang akan menang 4 kali dan kalah 6 kali. Hal ini memungkinkan pemain untuk tidak kehilangan minat dalam permainan, tetapi dalam hal apa pun, saldo keseluruhan tetap negatif - seseorang akan menang berkali-kali, tetapi juga kehilangan lebih sedikit .

Mungkin ini sudah sangat jelas, tetapi artikel ini hanya tentang permainan berdasarkan keacakan, bukan tentang poker, kartu, catur, dll. Bisakah ada "strategi kemenangan" dalam permainan acak seperti itu? Jelas tidak, karena baik tulang, bola, maupun tiket lotre tidak memiliki memori, dan perilaku mereka tidak bergantung pada iterasi sebelumnya. Ngomong-ngomong, penting untuk mengingat momen ini - secara intuitif, setelah kalah beberapa kali, seseorang dapat memutuskan bahwa sekarang ia akan "pasti" menang. Sayangnya, tidak ada roulette atau mati, dan mereka tidak tahu tentang jumlah upaya sebelumnya, setiap permainan pada dasarnya dimulai dengan yang bersih.

Menjawab pertanyaan dalam judul artikel - mungkinkah memenangkan taruhan? Seperti yang ditunjukkan oleh simulasi, pada prinsipnya dimungkinkan, teori probabilitas mengakui. Tapi tidak lama - ada baiknya mulai memainkan ke-2, ke-3, ... kali ke-9, saat saldo menurun. Dalam jangka panjang, tidak mungkin menang di kasino.

PS: Bagi mereka yang ingin bereksperimen, kode sumber dalam satu file diletakkan di bawah spoiler. Itu dapat dijalankan di IDE Python online, misalnya di sini . Untuk menguji roulette versi Eropa dan bukan roulette Amerika, cukup dengan mengubah kode 38 menjadi 37. Simulasi ini cukup mendasar, dan tidak memperhitungkan berbagai faktor tambahan, seperti jumlah uang yang dimiliki pemain atau batasan taruhan di kasino, mereka yang ingin dapat menambahkan semua ini secara mandiri. Di bawah spoiler, Anda juga dapat menonton versi video dari artikel ini.