Selain lelucon, topiknya serius, bahaya kebakaran. Ayo pergi. Ini adalah artikel ketiga dalam seri, yang membahas model untuk memperkirakan arus maksimum trek yang dicetak, yang dalam beberapa situasi merupakan parameter penentu ketika memilih ketebalan lapisan konduktif papan sirkuit cetak.
Dalam artikel
sebelumnya dikatakan bahwa pilihan ketebalan lapisan tembaga dari papan sirkuit tercetak ditentukan, pertama-tama, oleh jarak minimum yang diperlukan dan lebar minimum konduktor, serta arus maksimum yang mengalir melalui konduktor. Parameter-parameter ini dapat saling bertentangan: semakin tipis lapisan konduktif, semakin kecil pola topologi yang dapat diperoleh, tetapi semakin kecil arus maksimum yang dapat ditahan jalur cetak (ceteris paribus, lebar konduktor, frekuensi arus, heat sink, dll.). Energi termal Q yang dilepaskan pada hambatan ohmik R pada trek cetak (Joule heat Q = I
2 Rt, di mana saya adalah kekuatan saat ini, t adalah waktunya) menyebabkan temperaturnya meningkat relatif terhadap lingkungan, yang menyebabkan panas berlebih pada konduktor itu sendiri dan komponen terkait, atau, sebagai upaya terakhir, untuk terbakar pada arus yang membatasi (arus fusing bahasa Inggris). Korelasi antara arus melalui jalur pencetakan dan kenaikan suhu tergantung pada banyak parameter dan secara umum sulit untuk dibayangkan, namun, ada formula yang memungkinkan kita untuk membuat perkiraan awal.
Harga, Onderdonk dan Brooks
Salah satu upaya pertama dilakukan oleh W.H. Pris (WHPreece). Dia menerima ketergantungan empirisnya dalam percobaan laboratorium di mana dia secara bertahap meningkatkan arus melalui konduktor sampai bersinar merah. Formula Pris menghubungkan arus cahaya dengan diameter konduktor d untuk berbagai bahan:
di mana K adalah konstanta tabular kira-kira sama dengan 80 untuk tembaga. Dengan menggunakan rasio luas lingkaran, kita dapat menulis ulang rumus ini untuk kasus konduktor tembaga dengan luas penampang S:
Dalam percobaan Pris, konduktor ditangguhkan di udara, tidak seperti konduktor pada papan sirkuit tercetak, yang kondisinya sangat berbeda. Lebih dekat adalah kondisi pendingin untuk kasus-kasus konduktor penghubung tunggal, serta untuk beberapa kasus pengelasan microwire (ketika peracikan tidak digunakan untuk melindunginya), di mana formula ini dapat memberikan perkiraan yang baik untuk membatasi arus.
Peningkatan suhu jalur pencetakan yang dapat diterima biasanya dianggap 10-30 ° C. Nilai ini mungkin lebih besar tergantung pada parameter proyek, namun, pada seluruh rentang suhu operasi produk, suhu lintasan harus lebih kecil daripada suhu transisi kaca dari bahan papan sirkuit cetak (suhu transisi kaca Inggris,
Tg ) dan, terlebih lagi, suhu tembaga. Oleh karena itu, ketergantungan peningkatan suhu ∆T pada I saat ini dari jalur cetak lebar w dan ketebalan foil h, berguna oleh Brooks dalam [1], berguna:
di mana C, α, β, γ adalah konstanta, nilai-nilai yang untuk lapisan luar dan dalam diberikan pada tabel 1. Harus diingat bahwa pada lapisan luar ketebalan foil biasanya 20-40 mikron lebih besar dari nilai dasar karena penyemprotan tambahan saat membuat transisi lubang. Juga, efek hasil akhir pada papan tanpa topeng bisa signifikan. Ini digunakan dalam perangkat daya, ketika solder tambahan disolder ke jalur cetak dibuka dari topeng.
Formula lain yang terkenal untuk menghitung daya dukung arus utama dari sebuah konduktor adalah rumus Onderdonk (IMOnderdonk Inggris), yang berisi parameter penting seperti waktu. Ini menghubungkan waktu t dari lintasan arus I melalui konduktor tembaga dengan penampang S dan kenaikan suhu ∆T relatif terhadap suhu awal T
0 :
Karena dalam derivasi formula [2] setiap penghilangan panas dikecualikan, untuk kasus jalur pencetakan, rumus ini berlaku untuk pulsa arus pendek yang berlangsung hingga 1-2 detik. Dengan meningkatnya waktu dan pengaruh penghilangan panas, keakuratan estimasi menurun, secara signifikan menurunkan arus pembatas. Grafik dependensi untuk ketiga rumus di atas untuk berbagai parameter trek pencetakan ditunjukkan pada Gambar 1 dan 2.
Selalu penting untuk mempertimbangkan kondisi eksperimental atau asumsi analitik dalam derivasi untuk memahami batas-batas penerapan formula tertentu. Tak satu pun dari rumus di atas akan memberikan hubungan yang tepat dan optimal antara arus pembatas dan penampang konduktor yang diperlukan untuk aplikasi nyata. Hal yang sama berlaku untuk kalkulator sederhana yang dapat ditemukan di Internet (
misalnya ), karena mereka didasarkan pada formula ini atau yang serupa. Pengaruh konduktor dan komponen tetangga sebagai sumber dan penerima panas, radiasi, pendinginan aktif atau pasif dapat diperhitungkan hanya selama pemodelan termoelektrik dalam sistem CAD khusus (seperti Cadence, ANSYS dan lain-lain). Namun, bahkan dalam kasus ini, hasil pemodelan dan percobaan dapat sangat bervariasi. Faktanya adalah bahwa jalur pencetakan tidak memiliki bagian persegi panjang, tetapi dekat dengan trapesium (Gbr. 3), dan lebar dan nilai konduktivitas dari tembaga foil tidak hanya berbeda dari yang dihitung oleh model, tetapi juga memiliki beberapa pencar dari sampel ke sampel, batch untuk batch, produsen ke produsen, dll. Pengaruh penyimpangan lebar meningkat dengan penurunannya. Namun demikian, hasil yang dihitung dengan formula dan rekomendasi standar akan paling sering mewakili kasus terburuk, sehingga memberikan margin keselamatan bagi sistem. Jika pengembang perlu mengoptimalkan rasio antara arus yang membatasi dan bagian melintang yang diperlukan dari trek yang dicetak, maka perlu untuk mencapai tujuan ini dengan cara berulang-ulang pemodelan dan percobaan.

Efek kulit
Peningkatan penampang jalur cetak secara proporsional mengurangi hambatan ohmik per satuan panjang, yang mengurangi kehilangan panas selama aliran arus searah. Situasi dengan arus bolak-balik tidak begitu sederhana karena adanya efek kulit (efek kulit Inggris), yang mengarah pada fakta bahwa kerapatan arus bolak-balik tidak merata pada penampang melintang konduktor, secara eksponensial berkurang menjadi nol dari permukaan konduktor ke pusat. Untuk kenyamanan perhitungan, konsep bagian efektif konduktor dengan kedalaman yang ditentukan oleh rasio digunakan:
di mana f adalah frekuensi saat ini, σ adalah konduktivitas logam, μ adalah permeabilitas magnetik. Pada kedalaman yang sama dengan δ, kerapatan arus menjadi e kali lebih kecil dari kerapatan arus pada permukaan J
S. Secara matematis, perkiraan kesetaraan berikut dapat ditampilkan untuk kerapatan arus J (x, y) dalam konduktor:
Yaitu, untuk perhitungan perkiraan, kita dapat mengasumsikan bahwa arus hanya mengalir di lapisan batas konduktor perimeter l dari kedalaman δ, dan dengan distribusi yang seragam (Gbr. 4).

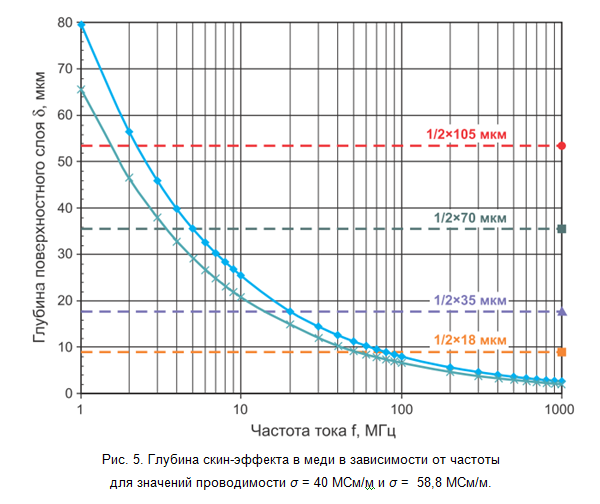
Dalam kerangka model yang disederhanakan ini, jika kedalaman lapisan permukaan kurang dari setengah ketebalan jalur pencetakan, impedansi jalur pencetakan pada frekuensi tertentu akan ditentukan oleh bagian efektif ini, yang mengarah pada peningkatan resistensi ohmik dan sedikit penurunan induktansi. Dalam gbr. Gambar 5 menunjukkan ketergantungan kedalaman lapisan permukaan pada frekuensi arus, dengan mempertimbangkan penyebaran konduktivitas dari tembaga yang diendapkan. Dapat dilihat dari hal itu bahwa untuk lapisan tembaga setebal 18 μm, frekuensi cutoff (di mana efek kulit berperan) berada di wilayah 50-70 MHz, dan untuk lapisan dengan ketebalan 35 μm berada di wilayah 15-20 MHz. Perhatikan bahwa pada frekuensi di atas 100 MHz kedalaman efek kulit sedikit bervariasi, ini memungkinkan kita untuk mengabaikan ketergantungannya pada frekuensi dalam perhitungan sinyal frekuensi tinggi.
Saat mendesain papan sirkuit tercetak dengan arus konstan beberapa ampere, perlu untuk melakukan perhitungan termal untuk komponen dan konduktor listrik. Model yang disajikan dan hubungan analitik memungkinkan kami untuk memperkirakan arus maksimum trek yang dicetak dan, atas dasar itu, pilih ketebalan lapisan tembaga yang diperlukan dan topologi konduktor. Untuk mendapatkan solusi yang tepat, perlu menggunakan sistem CAD khusus, sementara itu diinginkan untuk menentukan geometri dengan mempertimbangkan kesalahan manufaktur dan data konduktivitas tembaga yang diterima dari produsen papan sirkuit cetak. Saya sangat merekomendasikan membaca
artikel D. Brooks yang ditujukan untuk analisis rinci metode untuk memperkirakan suhu konduktor cetak, yang memberikan hasil visual dari pemodelan bidang suhu.
Sastra
[1] Brooks DG, Adam J. “Lacak Arus dan Suhu yang Diperiksa Kembali,” UltraCAD, 2015.
[2] Adam J., Brooks DG, "Dalam Mencari Preece dan Onderdonk," UltraCAD, 2015.
Artikel ini pertama kali diterbitkan dalam jurnal Components and Technologies 2018, No. 1. Publikasi di Geektimes telah disetujui oleh para editor majalah.