Kegagalan versi elegan asli dari struktur alam semesta

Delapan planet tata surya kita dan matahari kita, mengamati skala ukurannya, tetapi bukan skala orbitnya. Dengan mata telanjang, hal yang paling sulit untuk dilihat adalah Merkurius. Semua planet bergerak dalam orbit elips.

Teori-teori ilmiah terbaik adalah sederhana, tidak rumit, efektif memprediksi hasil pengamatan dan mengandung keanggunan batin. Persamaan paling sederhana dari Newton F = ma dan Einstein E = mc ² berisi informasi yang luar biasa dan memungkinkan kita untuk menyimpulkan begitu banyak dari mereka; model quark dan Relativitas Umum mudah dideskripsikan, tetapi mereka adalah teori yang sangat mendalam yang mengontrol interaksi partikel; ide-ide seperti supersimetri, teori unifikasi besar, dan teori string memperluas simetri yang diketahui fisika ke tingkat baru. Menerapkan teknik matematika baru ke Semesta, kami mencari kebenaran yang lebih dalam dalam kenyataan daripada tingkat pemahaman kami saat ini.

Model asli "Semesta elegan", Mysterium Cosmographicum [Rahasia Kepler Semesta], simetris, indah, dan berdasarkan matematika, yang belum pernah diterapkan sebelumnya. Tapi kisah peringatan kita tentang bagaimana itu ternyata juga merupakan kegagalan ilmiah yang besar.


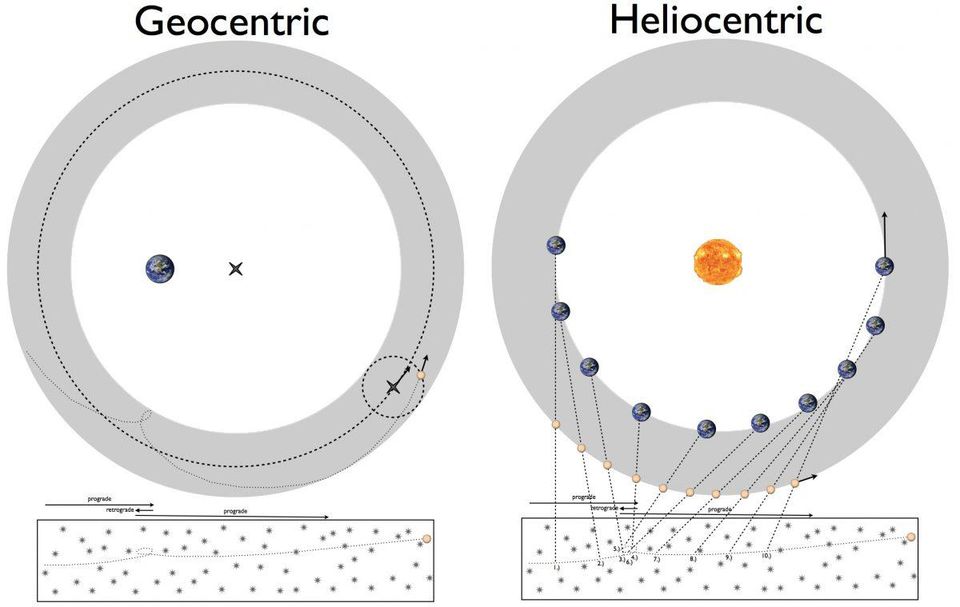Salah satu misteri terbesar abad ke-16 adalah bagaimana planet-planet bergerak. Ini dapat dijelaskan dengan menggunakan model Ptolemy geosentris (kiri) atau model Copernicus heliosentris (kanan). Namun, tidak satu pun dari mereka yang bisa menghitung semua detail dengan akurasi sewenang-wenang.

Sebelum Kepler, ada tiga sistem utama yang menggambarkan Semesta [tata surya dalam hal waktu itu]:

1. Model Ptolemeus, di mana Bumi tidak bergerak, dan segala sesuatu berputar di sekelilingnya dalam lingkaran, menggunakan equant , deferents dan epicycles .
2. Model Copernicus, di mana Matahari tidak bergerak dan Bumi adalah salah satu dari enam planet yang mengorbitnya, juga menggunakan epicycles.
3. Model Tycho Brahe, atau geo-heliosentris , di mana Matahari berputar di sekitar Bumi, dan semua planet lain di sekitar Matahari dalam lingkaran, juga menggunakan epicycles.

Kepler, menciptakan karya ilmiah beberapa dekade sebelum Galileo, berpikir sistem heliosentris menjanjikan, tetapi mereka membutuhkan lebih dari sekadar lingkaran. Dukungan mereka membutuhkan struktur matematika yang elegan. Sebagai seorang genius, pada usia 24 tahun, Kepler menerbitkan sebuah ide yang dianggapnya ide yang paling indah.


Kepler memutuskan bahwa harus ada tepat enam planet di tata surya dengan orbit yang didefinisikan secara tepat yang terletak di bidang yang tertulis dalam polyhedra biasa

Karena enam planet berputar mengelilingi Matahari (segala sesuatu di luar Saturnus hanya akan ditemukan 200 tahun kemudian), Kepler memutuskan bahwa harus ada enam orbit unik: satu untuk masing-masing planet. Tapi mengapa enam? Kenapa tidak lebih, mengapa tidak kurang? Mengapa ada jarak di antara mereka? Koneksi antara orbit dan matematika menjadi gagasannya tentang alam semesta yang elegan:

Saya berencana untuk menunjukkan bahwa Tuhan, yang menciptakan alam semesta dan menempatkan bola, ada dalam pikiran lima polihedron geometris biasa, dan membatasi ukuran, proporsi, dan pergerakan bola ke ukurannya.

Anda lihat, dalam tiga dimensi Anda dapat membuat tepat lima polihedra dari poligon biasa, tidak lebih dan tidak kurang. Mereka ditemukan oleh orang Yunani kuno 2000 tahun yang lalu, dan kadang-kadang mereka disebut Platonic polyhedra (walaupun mereka ditemukan jauh sebelum Plato). Kepler membayangkan sebuah sistem bola bersarang yang diuraikan dan ditulis di sekitar masing-masing polyhedron, menghasilkan enam orbit bola di sepanjang planet yang bergerak.


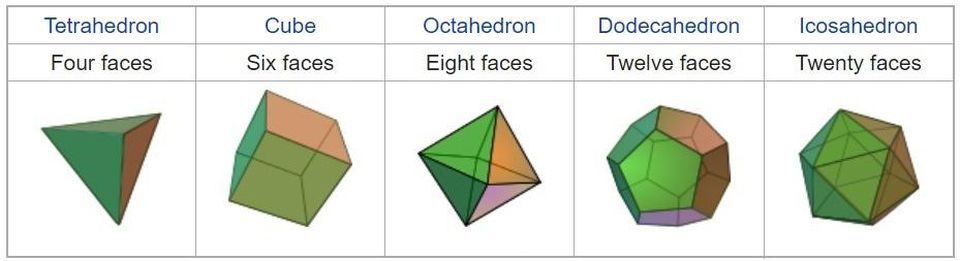Tetrahedron, hexahedron (kubus), octahedron, dodecahedron, icosahedron. Lima polihedra reguler, poligon tersusun dan reguler

Lingkungan Merkurius haruslah yang paling dalam, dan terletak di dalam octahedron, sebuah polyhedron biasa, yang terdiri dari delapan segitiga sama sisi. Di sekitarnya, bola Venus dideskripsikan - juga tertulis di icosahedron, sosok 20 sisi yang terdiri dari segitiga sama sisi. Di sekelilingnya dijelaskan bola Bumi yang tertulis di dodecahedron, 12 wajah di antaranya adalah segilima. Di sekitarnya dijelaskan bidang Mars yang tertulis dalam tetrahedron: sebuah polihedron tetrahedral dengan sisi-sisi berbentuk segitiga sama sisi. Di sekitar tetrahedron dijelaskan bola Yupiter, tertulis dalam kubus, poligon yang dihasilkan. Dan di sekitarnya dijelaskan bola terakhir, dengan orbit Saturnus.


Menurut teori Kepler, jari-jari relatif orbit planet-planet dapat dengan mudah dihitung. Namun, teori itu tidak lahir dari pengamatan (jelas perbedaan antara bidang Jupiter dan Mars dengan tetrahedron), dan Kepler harus membuangnya

Gagasan Kepler memang brilian; berdasarkan itu, adalah mungkin untuk secara akurat menghitung rasio jari-jari semua orbit. Masalahnya terungkap ketika membandingkan perhitungan dengan pengamatan. Rasio jari-jari yang dihitung dari orbit Merkurius dan Venus, Venus dan Bumi, Bumi dan Mars dalam perjanjian yang baik dengan kenyataan, tetapi dua dunia terakhir tidak dapat memenuhi jari-jari yang diprediksi oleh Kepler. Secara khusus, model itu dibantah oleh orbit Mars, yang tidak sesuai dengan lingkaran mana pun. Dan meskipun Kepler terus mengerjakannya, dan bahkan menerbitkan edisi kedua 20 tahun kemudian, kontribusinya yang paling penting adalah apa yang kebanyakan ilmuwan tidak dapat lakukan: untuk menjatuhkan hipotesis kesayangannya.


Orbit planet-planet tata surya bagian dalam tidak sepenuhnya melingkar, tetapi dekat dengan ini, dan paling menyimpang dari lingkaran Merkurius dan Mars. Selain itu, komet dan asteroid bergerak di sepanjang elips, mematuhi seluruh hukum Kepler, jika saja mereka secara gravitasi terhubung dengan Matahari.

Tapi itu bukan bola bersarang, tetapi elips yang berhasil memprediksi gerakan planet-planet dengan benar. Tiga undang-undang Kepler , mengenai pergerakan planet di elips di sekitar Matahari, pada area yang sama yang dijelaskan oleh jari-jari untuk periode waktu yang sama, dan tentang kesetaraan rasio kuadrat dari periode revolusi planet-planet dan kubus-sumbu semi-mayor dari orbit mereka, disangkal dan digantikan oleh Mysterium Cosmographicum. Keberhasilan orbit elips membuka jalan bagi hukum gravitasi universal Newton, dan melahirkan astrofisika. Terlepas dari cinta Kepler yang tak pudar untuk ide paling cemerlang, alam semesta lebih baik digambarkan oleh model yang kurang elegan. Setelah mengesampingkan harapannya dan membiarkan data eksperimen berperilaku lebih jauh, ia mampu mencapai terobosan yang tidak akan diperhatikan oleh orang yang kurang berbakat.


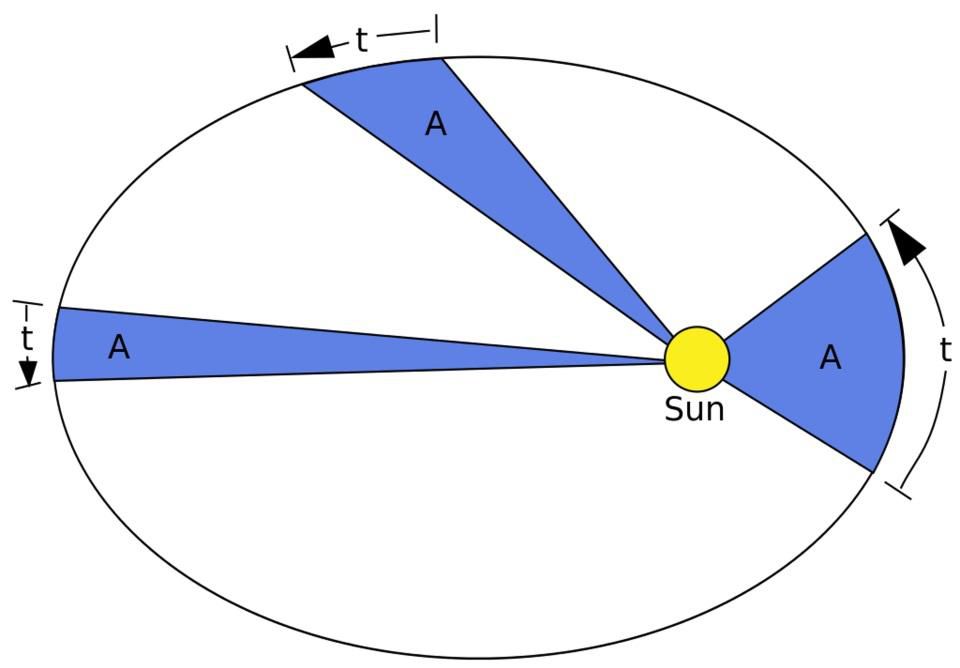Tiga hukum Kepler berlaku untuk sistem gravitasi apa pun serta tata surya.

Dalam fisika, ada godaan untuk menyerah pada reduksionisme: untuk menggambarkan fenomena sebanyak mungkin dengan sesedikit mungkin sarana. Gagasan tentang keberadaan teori segala sesuatu, satu-satunya teori yang mampu memprediksi dan menggambarkan segala sesuatu yang dapat dideskripsikan atau diprediksi di Semesta dengan akurasi setinggi mungkin, adalah impian dan tujuan akhir banyak ilmuwan. Namun, pada prinsipnya tidak ada jaminan bahwa mimpi seperti itu dapat terwujud. Seperti fisikawan terkenal Lincoln Wulfenstein menulis:

Pelajaran Kepler bukanlah bahwa kita harus menahan diri untuk tidak mengajukan pertanyaan yang tampaknya mendasar; pelajarannya adalah kita tidak diberikan untuk mencari tahu apakah ada jawaban sederhana untuk mereka, dan di mana mereka dapat ditemukan.

Keanggunan, keindahan, dan reduksionisme dapat membuka peluang luar biasa untuk prediksi sukses fenomena fisik baru, tetapi tidak ada jaminan bahwa prediksi ini akan menjadi kenyataan. Membuat terobosan baru dalam sains fundamental, banyak mimpi berbagi impian dan harapan kami untuk mendekati teori pemersatu segalanya dengan bantuan keindahan matematika dan simetri tambahan, tetapi tidak ada yang menjamin mereka. Semoga kita semua terbuka pada fakta bahwa kita diberi tahu data, seperti Kepler, dan kita bisa mengikuti mereka di mana pun mereka menuntun kita.