Di blog kami di Habré, kami menerbitkan terjemahan bahan yang disesuaikan dari blog The Financial Hacker, yang ditujukan untuk pertanyaan tentang menciptakan strategi untuk perdagangan di bursa. Sebelumnya, kami membahas
pencarian inefisiensi pasar , pembuatan
model strategi perdagangan , dan
prinsip -
prinsip pemrograman mereka . Hari ini kita
akan fokus pada penggunaan pendekatan pembelajaran mesin untuk meningkatkan efisiensi sistem perdagangan.
Komputer pertama yang memenangkan Kejuaraan Catur Dunia adalah Deep Blue. Itu pada tahun 1996, dan dua puluh tahun berlalu sebelum program lain, Alpha Go, berhasil mengalahkan pemain terbaik di Go. Deep Blue adalah sistem berorientasi model dengan aturan catur tertanam. AplhaGo adalah sistem penambangan data, jaringan saraf yang dalam, dilatih menggunakan ribuan game di Go. Yaitu, untuk mengambil langkah dari kemenangan atas orang-orang yang menjadi juara dalam catur, untuk mendominasi pemain top di Go, itu perlu bukan sepotong besi yang ditingkatkan, tetapi sebuah terobosan di bidang perangkat lunak.
Dalam artikel saat ini, kami akan mempertimbangkan penerapan pendekatan penambangan data untuk menciptakan strategi perdagangan. Metode ini tidak memperhitungkan mekanisme pasar, melainkan hanya memindai kurva harga dan sumber data lainnya untuk mencari pola prediksi. Pembelajaran mesin atau "kecerdasan buatan" tidak selalu diperlukan untuk ini. Sebaliknya, sangat sering, metode yang paling populer dan menguntungkan dari pekerjaan penambangan data tanpa embel-embel dalam bentuk jaringan saraf atau dukungan untuk metode vektor.
Prinsip Pembelajaran Mesin
Algoritma yang terlatih diumpankan dengan sampel data, biasanya entah bagaimana diekstraksi dari harga pertukaran historis. Setiap sampel terdiri dari n variabel x1 ... xn, yang biasanya disebut prediktor, fungsi, sinyal atau, lebih sederhana, memasukkan data. Prediktor ini dapat berupa harga n bar terakhir pada grafik harga atau sekumpulan nilai indikator klasik, atau fungsi lain dari kurva harga (bahkan ada kasus ketika piksel individual dari grafik harga digunakan sebagai prediktor untuk jaringan saraf!). Setiap sampel juga biasanya berisi variabel target tertentu y, misalnya, hasil dari transaksi berikutnya setelah menganalisis sampel atau pergerakan harga berikutnya.
Dalam literatur, y sering disebut sebagai label atau tujuan. Dalam proses pembelajaran, algoritma belajar untuk memprediksi target y berdasarkan pada prediksi x1 ... xn. Apa yang “diingat” oleh sistem dalam proses disimpan dalam struktur data yang disebut model yang spesifik untuk algoritma tertentu (penting untuk tidak membingungkan konsep ini dengan model keuangan atau strategi berorientasi model). Model pembelajaran mesin dapat berfungsi dengan aturan prediksi yang ditulis menggunakan kode C yang dihasilkan oleh proses pembelajaran. Atau itu bisa berupa seperangkat bobot terkait jaringan saraf:
Pelatihan: x1 ... xn, y => model
Prediksi: x1 ... xn, model => y
Prediktor, fungsi, atau apa pun yang Anda ingin menyebutnya, harus berisi informasi yang cukup untuk menghasilkan prediksi tentang nilai target y dengan akurasi tertentu. Mereka juga harus memenuhi dua kriteria formal. Pertama, semua nilai prediktor harus dalam kisaran yang sama, misalnya, -1 ... +1 (untuk sebagian besar algoritma pada R) atau -100 ... +100 (untuk algoritma dalam bahasa skrip Zorro atau TSSB). Jadi sebelum mengirim data ke sistem, Anda harus menormalkannya. Kedua, sampel harus seimbang, yaitu terdistribusi secara merata atas nilai-nilai variabel target. Artinya, Anda harus memiliki jumlah sampel yang sama yang mengarah ke hasil positif, dan kehilangan set. Jika kedua persyaratan ini tidak diikuti, maka hasil yang baik tidak akan berhasil.
Algoritma regresi menghasilkan prediksi tentang nilai numerik, seperti magnitude atau tanda pergerakan harga berikutnya. Algoritma klasifikasi memprediksi kelas kuantitatif sampel, misalnya, apakah mereka mendahului laba atau rugi dana. Beberapa algoritma, seperti jaringan saraf, pohon keputusan, atau metode vektor dukungan, dapat dijalankan di kedua mode.
Ada juga algoritma yang dapat belajar untuk mengekstrak dari sampel kelas tanpa perlu target y. Ini disebut pembelajaran tanpa pengawasan, sebagai lawan dari pembelajaran yang diawasi. Di antara dua metode ini terdapat “penguatan pembelajaran”, di mana sistem melatih dengan menjalankan simulasi dengan fungsi yang ditentukan dan menggunakan hasilnya sebagai tujuan. Seorang pengikut AlphaGo, sistem yang disebut AlphaZero menggunakan pembelajaran yang diperkuat, memainkan sejuta game Go dengan sendirinya. Di bidang keuangan, sistem atau produk seperti itu yang menggunakan pembelajaran tanpa pengawasan sangat jarang. 99% sistem menggunakan pembelajaran terawasi.
Sinyal apa pun yang kami gunakan untuk prediktor di bidang keuangan, dalam kebanyakan kasus, sinyal-sinyal itu akan mengandung banyak kebisingan dan sedikit informasi, dan selain itu mereka akan limbung. Jadi prediksi keuangan adalah salah satu tugas paling sulit dari pembelajaran mesin. Algoritma yang lebih kompleks di sini mencapai hasil yang lebih baik. Pemilihan prediktor sangat penting untuk kesuksesan. Tidak harus ada banyak dari mereka, karena ini mengarah pada pelatihan ulang dan kegagalan fungsi. Oleh karena itu, strategi penambangan data sering menggunakan algoritma yang dipilih sebelumnya yang mengekstraksi sejumlah kecil prediktor dari kumpulan yang lebih luas. Seleksi awal semacam itu mungkin didasarkan pada korelasi antara prediktor, signifikansi mereka, kekayaan informasi, atau hanya keberhasilan / kegagalan penggunaan rangkaian uji. Eksperimen praktis dengan pemilihan target dapat ditemukan, misalnya, di blog
Kekayaan Robot .
Di bawah ini adalah daftar metode penambangan data yang paling populer digunakan di bidang keuangan.
1. Sup indikator
Sebagian besar sistem perdagangan tidak didasarkan pada model keuangan. Seringkali pedagang hanya memerlukan sinyal perdagangan yang dihasilkan oleh indikator teknis tertentu, yang disaring oleh indikator lain dalam kombinasi dengan indikator teknis tambahan. Ketika bertanya kepada seorang trader tentang bagaimana kecelakaan indikator semacam itu dapat menghasilkan semacam keuntungan, ia biasanya menjawab sesuatu seperti: "Percayalah, saya berdagang tangan saya dan semuanya berfungsi."
Dan itu benar. Setidaknya terkadang. Meskipun sebagian besar sistem ini tidak akan lulus
tes WFA (dan beberapa hanya menguji data historis), sejumlah besar sistem seperti itu pada akhirnya bekerja dan menghasilkan keuntungan. Penulis blog Peretas Keuangan terlibat dalam pengembangan sistem perdagangan khusus, dan menceritakan kisah salah satu klien yang secara sistematis bereksperimen dengan indikator teknis hingga ia menemukan kombinasi yang berfungsi untuk jenis aset tertentu. Metode trial and error ini adalah pendekatan klasik untuk penambangan data, untuk kesuksesan Anda hanya membutuhkannya, keberuntungan dan banyak uang untuk tes. Akibatnya, terkadang Anda dapat mengandalkan sistem yang menguntungkan.
2. Pola kandil
Jangan dikelirukan dengan pola kandil yang telah ada selama ratusan tahun. Setara modern dari pendekatan ini adalah perdagangan berdasarkan pergerakan harga. Anda juga menganalisis indikator terbuka, tinggi, rendah dan dekat untuk setiap lilin di grafik. Tapi sekarang Anda menggunakan data mining untuk menganalisis lilin kurva harga untuk menyoroti pola yang dapat digunakan untuk menghasilkan prediksi tentang arah pergerakan harga di masa depan.
Ada seluruh paket perangkat lunak untuk tujuan ini. Mereka mencari pola yang menguntungkan dalam hal kriteria yang ditentukan pengguna, dan menggunakannya untuk membangun fungsi deteksi pola. Semua ini mungkin terlihat seperti ini:
int detect(double* sig) { if(sig[1]<sig[2] && sig[4]<sig[0] && sig[0]<sig[5] && sig[5]<sig[3] && sig[10]<sig[11] && sig[11]<sig[7] && sig[7]<sig[8] && sig[8]<sig[9] && sig[9]<sig[6]) return 1; if(sig[4]<sig[1] && sig[1]<sig[2] && sig[2]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[7]<sig[8] && sig[10]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && eqF(sig[4]-sig[5]) && sig[5]<sig[2] && sig[2]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && sig[4]<sig[5] && sig[5]<sig[2] && sig[2]<sig[0] && sig[0]<sig[3] && sig[7]<sig[8] && sig[10]<sig[11] && sig[11]<sig[9] && sig[9]<sig[6]) return 1; if(sig[1]<sig[2] && sig[4]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[7]<sig[8] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; .... return 0; }
Fungsi C ini mengembalikan 1 ketika sinyal cocok dengan salah satu pola, jika tidak maka mengembalikan 0. Kode panjang tampaknya mengisyaratkan bahwa ini bukan cara tercepat untuk mencari pola. Lebih baik menggunakan pendekatan di mana fungsi deteksi tidak perlu diekspor, tetapi dapat mengurutkan sinyal berdasarkan kepentingannya dan mengurutkannya. Contoh dari sistem tersebut dapat ditemukan
di tautan .
Bisakah perdagangan dengan harga berhasil? Seperti dalam kasus sebelumnya, metode ini tidak didasarkan pada model keuangan rasional apa pun. Pada saat yang sama, semua orang memahami bahwa peristiwa tertentu di pasar dapat memengaruhi pesertanya, sebagai akibatnya pola prediksi jangka pendek muncul. Tetapi jumlah pola seperti itu tidak bisa besar jika Anda hanya mempelajari urutan beberapa lilin berurutan pada grafik. Maka Anda perlu membandingkan hasilnya dengan data lilin, yang tidak ada di dekatnya, tetapi, sebaliknya, dipilih secara acak dalam periode waktu yang lebih lama. Dalam hal ini, Anda akan mendapatkan jumlah pola yang hampir tak terbatas - dan berhasil melepaskan diri dari konsep realitas dan rasionalitas. Sulit membayangkan bagaimana harga di masa depan dapat diprediksi berdasarkan beberapa nilainya minggu lalu. Meskipun demikian, banyak pedagang bekerja ke arah ini.
3. Regresi linier
Dasar sederhana untuk banyak algoritma pembelajaran mesin yang kompleks: untuk memprediksi variabel target y menggunakan kombinasi linear dari prediktor x1 ... xn.

Odds - ini adalah model. Mereka dihitung untuk meminimalkan jumlah penyimpangan kuadrat antara nilai-nilai y nyata, nilai-nilai pelatihan dan prediksi y sesuai dengan rumus:

Untuk sampel yang terdistribusi normal, minimalisasi dimungkinkan menggunakan operasi matriks, sehingga iterasi tidak diperlukan. Dalam kasus ketika n = 1 - dengan hanya satu prediktor x, rumus regresi dikurangi menjadi:
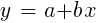
- yaitu, sebelum regresi linier sederhana, dan ketika n> 1 regresi linier akan multivarian. Regresi linier sederhana tersedia di sebagian besar platform perdagangan, misalnya, indikator
LinReg di TA-Lib. Ketika y = harga dan x = waktu, itu dapat digunakan sebagai alternatif untuk moving average. Dalam platform R, regresi tersebut diimplementasikan oleh fungsi pengiriman standar lm (..). Itu juga dapat diwakili oleh regresi polinomial. Seperti dalam kasus paling sederhana, di sini kita menggunakan satu variabel prediktif x, tetapi juga kuadrat dan derajat berikutnya, jadi xn == xn:
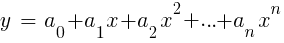
Jika n = 2 atau n = 3, regresi polinomial sering digunakan untuk memprediksi harga rata-rata berikutnya dari harga smoothed dari bar terakhir. Untuk regresi polinomial, fungsi polyfit dari MatLab, R, Zorro dan banyak platform lainnya dapat digunakan.
4. Perceptron
Seringkali itu disebut jaringan saraf dengan hanya satu neuron. Faktanya, perceptron adalah fungsi regresi, seperti dijelaskan di atas, tetapi dengan hasil biner, yang karenanya disebut
regresi logistik . Meskipun, secara umum, ini bukan regresi, tetapi algoritma klasifikasi. Misalnya, fungsi saran (PERCEPTRON, ...) dari kerangka kerja Zorro menghasilkan kode C yang mengembalikan 100 atau -100 tergantung pada apakah hasil yang diprediksi adalah ambang batas atau tidak:
int predict(double* sig) { if(-27.99*sig[0] + 1.24*sig[1] - 3.54*sig[2] > -21.50) return 100; else return -100; }
Seperti yang Anda lihat, array sig setara dengan fungsi xn dalam rumus regresi, dan koefisien a adalah faktor digital.
5. Jaringan saraf
Regresi linier atau logistik hanya dapat menyelesaikan masalah linier. Pada saat yang sama, tugas perdagangan seringkali tidak sesuai dengan kategori ini. Contoh terkenal adalah prediksi output dari fungsi XOR sederhana. Ini juga termasuk prediksi untung dari transaksi. Jaringan saraf tiruan (JST) dapat memecahkan masalah non-linear. Ini adalah seperangkat perceptrons yang terhubung ke array level yang berbeda. Setiap perceptron adalah neuron jaringan. Outputnya menjadi input ke neuron lain dari tingkat berikut:
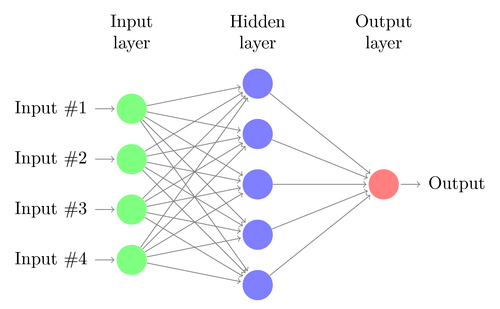
Seperti perceptron, jaringan saraf dilatih dengan menentukan koefisien yang meminimalkan kesalahan antara prediksi dan target dalam sampel. Ini membutuhkan proses perkiraan, biasanya dengan propagasi kembali kesalahan dari output ke input dengan optimalisasi bobot di sepanjang jalan. Proses ini memiliki dua keterbatasan. Pertama, output neuron harus merupakan fungsi yang dapat dibedakan secara terus-menerus, bukan ambang sederhana untuk perceptron. Kedua, jaringan seharusnya tidak terlalu dalam - keberadaan sejumlah besar level neuron yang tersembunyi antara input dan output hanya membahayakan data. Batasan kedua ini membatasi kompleksitas masalah yang dapat diselesaikan oleh jaringan saraf standar.
Saat menggunakan jaringan saraf untuk memprediksi transaksi, Anda akan memiliki banyak parameter yang dapat dimanipulasi, yang, jika dilakukan secara tidak akurat, dapat mengakibatkan munculnya bias seleksi:
- jumlah level tersembunyi;
- jumlah neuron di setiap tingkat tersembunyi;
- jumlah siklus backpropagation - zaman;
- tingkat pelatihan, lebar langkah era;
- momentum, faktor kelembaman untuk adaptasi bobot;
- fungsi aktivasi.
Fungsi aktivasi mengemulasi ambang perceptron. Untuk propagasi balik, Anda memerlukan fungsi yang dapat dibedakan secara konstan yang menghasilkan langkah lunak untuk nilai x tertentu. Biasanya, fungsi sigmoid, tanh, atau softmax digunakan untuk ini. Terkadang fungsi linear digunakan yang mengembalikan jumlah tertimbang dari semua data input. Dalam hal ini, jaringan dapat digunakan untuk regresi, prediksi nilai numerik, bukan output biner.
Jaringan saraf termasuk dalam pengiriman paket standar R (misalnya, nnet adalah jaringan dengan satu tingkat tersembunyi), serta dalam banyak paket lainnya (seperti RSNNS dan FCNN4R).
6. Pembelajaran yang mendalam
Metode pembelajaran mendalam menggunakan jaringan saraf dengan banyak level tersembunyi dan ribuan neuron yang tidak dapat dilatih secara efektif menggunakan propagasi balik sederhana. Dalam beberapa tahun terakhir, beberapa metode telah menjadi populer untuk melatih jaringan besar tersebut. Mereka biasanya melibatkan pra-pelatihan tingkat neuron tersembunyi untuk meningkatkan efektivitas pembelajaran dasar.
Restricted Boltzmann Machine (RBM) adalah algoritma klasifikasi yang tidak terkontrol dengan struktur jaringan khusus di mana tidak ada koneksi antara neuron tersembunyi. Sparse Auto Encoder (SAE) menggunakan struktur jaringan yang biasa, tetapi pra-melatih lapisan tersembunyi dengan cara tertentu, mereproduksi sinyal input pada tingkat output dengan sesedikit mungkin koneksi aktif. Metode-metode ini memungkinkan Anda untuk menerapkan jaringan yang sangat kompleks untuk menyelesaikan masalah pembelajaran yang sangat kompleks. Misalnya, tugas mengalahkan orang terbaik yang bermain Go.
Jaringan deep learning termasuk dalam paket deepnet dan darch untuk R. Deepnet termasuk auto-encoder, dan darch termasuk mesin Boltzmann. Di bawah ini adalah contoh kode yang menggunakan deepnet dengan tiga level tersembunyi untuk memproses sinyal perdagangan melalui fungsi neor () dari framework Zorro:
library('deepnet', quietly = T) library('caret', quietly = T) # called by Zorro for training neural.train = function(model,XY) { XY <- as.matrix(XY) X <- XY[,-ncol(XY)] # predictors Y <- XY[,ncol(XY)] # target Y <- ifelse(Y > 0,1,0) # convert -1..1 to 0..1 Models[[model]] <<- sae.dnn.train(X,Y, hidden = c(50,100,50), activationfun = "tanh", learningrate = 0.5, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 100, batchsize = 100, hidden_dropout = 0, visible_dropout = 0) } # called by Zorro for prediction neural.predict = function(model,X) { if(is.vector(X)) X <- t(X) # transpose horizontal vector return(nn.predict(Models[[model]],X)) } # called by Zorro for saving the models neural.save = function(name) { save(Models,file=name) # save trained models } # called by Zorro for initialization neural.init = function() { set.seed(365) Models <<- vector("list") } # quick OOS test for experimenting with the settings Test = function() { neural.init() XY <<- read.csv('C:/Project/Zorro/Data/signals0.csv',header = F) splits <- nrow(XY)*0.8 XY.tr <<- head(XY,splits) # training set XY.ts <<- tail(XY,-splits) # test set neural.train(1,XY.tr) X <<- XY.ts[,-ncol(XY.ts)] Y <<- XY.ts[,ncol(XY.ts)] Y.ob <<- ifelse(Y > 0,1,0) Y <<- neural.predict(1,X) Y.pr <<- ifelse(Y > 0.5,1,0) confusionMatrix(Y.pr,Y.ob) # display prediction accuracy }
7. Mendukung vektor
Seperti halnya jaringan saraf, metode vektor dukungan adalah perpanjangan lain dari regresi linier. Jika Anda melihat rumus regresi lagi:

Kemudian seseorang dapat menginterpretasikan fungsi xn sebagai koordinat ruang n-dimensi. Menetapkan variabel target y ke nilai tetap akan menentukan bidang di ruang ini - itu akan disebut hyperplane, karena sebenarnya ia akan memiliki dua (bahkan n-1) ukuran. Hyperplane memisahkan sampel dengan y> 0 dari yang mana y <0. Koefisien a dapat dihitung sebagai lintasan yang memisahkan pesawat dari sampel terdekat - vektor pendukungnya, dengan demikian nama algoritma. Dengan demikian, kita mendapatkan classifier biner dengan pemisahan optimal dari sampel menang dan kalah.
Masalah: biasanya sampel ini tidak dapat dibagi secara linear - mereka dikelompokkan secara acak dalam ruang fungsi. Tidak mungkin untuk menggambar bidang yang halus antara opsi yang menang dan yang kalah, jika ini bisa dilakukan, maka untuk perhitungannya orang dapat menggunakan metode yang lebih sederhana seperti analisis diskriminan linier. Namun dalam kasus umum, Anda dapat menggunakan trik ini: tambahkan lebih banyak ukuran ke ruang. Dalam hal ini, algoritma vektor dukungan akan dapat menghasilkan lebih banyak parameter dengan fungsi nuklir yang menggabungkan dua prediktor - mirip dengan transisi dari regresi sederhana ke polinomial. Semakin banyak ukuran yang Anda tambahkan, semakin mudah untuk membagi sampel dengan hyperplane. Kemudian dapat dikonversi kembali ke ruang n-dimensi asli.
Seperti jaringan saraf, vektor referensi dapat digunakan tidak hanya untuk klasifikasi, tetapi juga untuk regresi. Mereka juga menawarkan sejumlah opsi untuk optimasi dan kemungkinan pelatihan ulang:
- Fungsi kernel - kernel RBF (fungsi basis radial, kernel simetris) biasanya digunakan, tetapi kernel lain dapat dipilih, misalnya, sigmoid, polinom dan linear.
- Gamma - Lebar inti RBF.
- Parameter biaya C, “penalti” untuk klasifikasi sampel pelatihan yang salah.
Perpustakaan libsvm sering digunakan, yang tersedia dalam paket e1071 untuk R.
8. Algoritma k-tetangga terdekat
Dibandingkan dengan JST dan SVM yang berat, ini adalah algoritma yang sederhana dan menyenangkan dengan properti yang unik: tidak perlu dilatih. Sampel akan menjadi model. Algoritma ini dapat digunakan untuk sistem perdagangan yang terus-menerus dilatih dengan menambahkan sampel baru. Algoritma ini menghitung jarak dalam ruang fungsi dari nilai saat ini ke sampel k-terdekat. Jarak dalam ruang n-dimensi antara dua set (x1 ... xn) dan (y1 ... yn) dihitung dengan rumus:
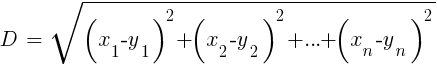
Algoritma hanya memprediksi target dari rata-rata variabel target k dari sampel terdekat, dibobot oleh jarak pengembaliannya. Ini dapat digunakan untuk klasifikasi dan regresi. Untuk memprediksi tetangga terdekat, Anda dapat memanggil fungsi knn di R atau menulis kode C sendiri untuk tujuan ini.
9. K-means
Ini adalah algoritma perkiraan untuk klasifikasi yang tidak terkontrol. Ini agak mirip dengan algoritma sebelumnya. Untuk mengklasifikasikan sampel, algoritma pertama menempatkan titik acak k dalam ruang fungsi. Kemudian ia menetapkan ke salah satu titik ini semua sampel dengan jarak terkecil ke sana. Kemudian titik tersebut bergeser ke tengah dari nilai-nilai terdekat ini. Ini menghasilkan binding sampel baru, karena beberapa dari mereka sekarang akan lebih dekat ke titik lain. Proses ini diulang sampai referensi ulang sebagai hasil dari pergeseran titik berhenti, yaitu, sampai setiap titik rata-rata untuk sampel terdekat. Sekarang kita memiliki kelas sampel k, masing-masing terletak di sebelah titik-k.
Algoritma sederhana ini dapat menghasilkan hasil yang sangat baik. Dalam R, fungsi kmeans digunakan untuk mengimplementasikannya, contoh algoritma dapat ditemukan
di tautan .
10. Naif Bayes
Algoritma ini menggunakan teorema Bayesian untuk mengklasifikasikan sampel fungsi non-numerik (peristiwa), seperti pola lilin yang disebutkan di atas. Misalkan peristiwa X (misalnya, parameter Buka bilah sebelumnya di bawah parameter Buka bilah saat ini) muncul di 80% dari sampel yang menang. Lalu berapa kemungkinan memenangkan sampel di hadapan event X di dalamnya? Ini bukan 0,8 seperti yang mungkin Anda pikirkan. Probabilitas ini dihitung dengan rumus:
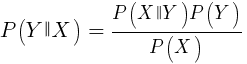
P (Y | X) adalah probabilitas bahwa peristiwa Y (laba) akan terjadi di semua sampel yang mengandung peristiwa X (dalam contoh kami, Buka (1) <Buka (0)). Sesuai dengan rumus, itu sama dengan probabilitas kemunculan peristiwa X di semua sampel pemenang (dalam kasus kami 0.8), dikalikan dengan probabilitas Y di semua sampel (sekitar 0,5 jika Anda mengikuti kiat menyeimbangkan sampel) dan dibagi dengan probabilitas kemunculan X di semua sampel.
Jika kita naif dan menganggap bahwa semua peristiwa X tidak tergantung satu sama lain, maka kita dapat menghitung probabilitas total bahwa sampel akan menang dengan hanya mengalikan probabilitas P (X | menang) untuk setiap peristiwa X. Kemudian kita sampai pada rumus berikut:
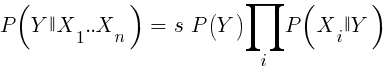
Dengan faktor penskalaan s. Agar formula dapat berfungsi, fungsi harus dipilih sedemikian rupa sehingga dapat sebebas mungkin. Ini akan menjadi hambatan untuk menggunakan Bayes yang naif untuk berdagang. Misalnya, dua acara Tutup (1) <Tutup (0) dan Buka (1) <Buka (0) kemungkinan besar tidak saling terpisah. Prediktor numerik dapat dikonversi ke acara dengan membagi angka menjadi rentang yang terpisah. Naive Bayes tersedia dalam paket e1071 untuk R.
11. Pohon keputusan dan regresi
Pohon tersebut memprediksi hasil nilai numerik berdasarkan rantai keputusan dalam format ya / tidak dalam struktur cabang pohon. Setiap keputusan mewakili ada atau tidak adanya peristiwa (dalam hal nilai non-numerik) atau perbandingan nilai dengan ambang batas yang ditetapkan. Fungsi pohon yang khas, yang dihasilkan, misalnya, oleh kerangka kerja Zorro, terlihat seperti ini:
int tree(double* sig) { if(sig[1] <= 12.938) { if(sig[0] <= 0.953) return -70; else { if(sig[2] <= 43) return 25; else { if(sig[3] <= 0.962) return -67; else return 15; } } } else { if(sig[3] <= 0.732) return -71; else { if(sig[1] > 30.61) return 27; else { if(sig[2] > 46) return 80; else return -62; } } } }
Bagaimana pohon seperti itu diperoleh dari serangkaian sampel? Mungkin ada beberapa metode untuk ini, termasuk
entropi informasi Shannon .
Pohon keputusan dapat digunakan secara luas. Sebagai contoh, mereka cocok untuk menghasilkan prediksi yang lebih akurat daripada yang dapat dicapai menggunakan jaringan saraf atau vektor referensi. Namun, ini bukan solusi universal. Algoritma yang paling dikenal dari jenis ini adalah C5.0, tersedia dalam paket C50 untuk R.
Untuk lebih meningkatkan kualitas prediksi, Anda dapat menggunakan set pohon - mereka disebut hutan acak. Algoritma ini tersedia dalam paket R yang disebut randomForest, ranger, dan Rborist.
Kesimpulan
Ada banyak metode penambangan data dan pembelajaran mesin. Pertanyaan kritis di sini adalah ini: mana yang lebih baik, strategi berbasis model atau pembelajaran mesin? Tidak ada keraguan bahwa pembelajaran mesin memiliki sejumlah keunggulan. Misalnya, Anda tidak perlu peduli dengan mikrostruktur pasar, ekonomi, pertimbangkan filosofi pelaku pasar atau hal serupa lainnya. Anda dapat berkonsentrasi pada matematika murni. Pembelajaran mesin adalah cara yang jauh lebih elegan dan menarik untuk menciptakan sistem perdagangan. Di pihaknya, semua keuntungan, kecuali satu - selain cerita di forum pedagang, keberhasilan metode ini dalam perdagangan nyata sulit dilacak.
Hampir setiap minggu, artikel baru diterbitkan tentang perdagangan menggunakan pembelajaran mesin. Materi seperti itu harus diambil dengan skeptisisme yang adil. Beberapa penulis mengklaim tingkat kemenangan fantastis 70%, 80%, atau bahkan 85%. Namun, beberapa orang mengatakan bahwa Anda dapat kehilangan uang bahkan jika prediksi itu menang. Akurasi 85% biasanya diterjemahkan menjadi indikator profitabilitas di atas 5 - jika semuanya begitu sederhana, maka pencipta sistem seperti itu sudah akan menjadi miliarder. Namun, untuk beberapa alasan, mereproduksi hasil yang sama hanya dengan mengulangi metode yang dijelaskan dalam artikel gagal.
Dibandingkan dengan sistem berbasis model, ada beberapa sistem pembelajaran mesin yang sangat sukses. Misalnya, mereka jarang digunakan oleh dana lindung nilai yang sukses. Mungkin di masa depan, ketika kekuatan komputasi menjadi lebih mudah diakses, sesuatu akan berubah, tetapi untuk saat ini, algoritma pembelajaran yang mendalam tetap lebih merupakan hobi yang menarik bagi para geek daripada alat penghasil uang nyata di bursa.
Materi terkait pasar keuangan dan saham lainnya dari ITI Capital :