Untuk memeriksa persamaan Einstein, Anda perlu menendang lubang hitam

Dua tim peneliti telah membuat kemajuan yang signifikan dalam membuktikan hipotesis stabilitas lubang hitam, tes matematika paling penting dari Teori Relativitas Umum Einstein.

Pada November 1915, pada sebuah kuliah di Akademi Ilmu Pengetahuan Prusia, Albert Einstein menggambarkan sebuah ide yang mengubah umat manusia di sekitar alam semesta. Alih-alih mengambil geometri ruang dan waktu tetap, Einstein menjelaskan bahwa kita hidup dalam realitas empat dimensi yang disebut ruang-waktu, yang bentuknya berfluktuasi dalam menanggapi materi dan energi.

Einstein menggambarkan ide penting ini secara terperinci dalam beberapa persamaan yang disebut " persamaan Einstein " (atau persamaan medan gravitasi) yang membentuk inti dari GTR-nya. Teori ini dikonfirmasi oleh semua tes eksperimental yang menjadi sasarannya pada abad berikutnya.

Dan meskipun teori Einstein tampaknya menggambarkan dunia yang diamati, matematika yang mendasari sebagian besar tetap misterius. Matematikawan mampu memberikan sedikit bukti tentang persamaan itu sendiri. Kita tahu bahwa itu berhasil, tetapi kita tidak bisa mengatakan dengan tepat mengapa. Bahkan Einstein harus kembali ke perkiraan, dan bukan ke solusi yang tepat, untuk melihat Semesta melalui lensa yang ia ciptakan.

Tetapi selama setahun terakhir, matematikawan telah membawa matematika GR ke fokus yang lebih jelas. Dua kelompok muncul dengan solusi yang berkaitan dengan masalah penting dalam GR, yang dikenal sebagai hipotesis stabilitas lubang hitam. Karya mereka membuktikan bahwa persamaan Einstein sesuai dengan intuisi fisik untuk perilaku ruang-waktu: jika Anda menerapkan gangguan tajam padanya, itu akan mengejutkan seperti jeli, dan kemudian akan tenang dalam keadaan mantap, dari mana semuanya dimulai.

“Jika keputusan itu tidak stabil, itu berarti bahwa itu tidak fisik. Ini akan menjadi hantu matematika yang ada dalam matematika, tetapi tidak masalah dari sudut pandang fisika, ”kata Sergiu Kleinerman , ahli matematika di Universitas Princeton, dan penulis, bersama dengan Jeremy Szeftel , dari salah satu dari dua hasil .

Untuk melengkapi buktinya, matematikawan perlu memecahkan kompleksitas dasar persamaan Einstein. Untuk menggambarkan evolusi bentuk ruang-waktu, Anda memerlukan sistem koordinat - sesuatu seperti garis lintang dan bujur - yang memberi tahu Anda di mana beberapa titik berada. Dan dalam ruang-waktu sangat sulit untuk menemukan sistem koordinat yang bekerja di mana-mana.

Kocok lubang hitam

Seperti yang Anda ketahui, GR menggambarkan ruang-waktu sebagai sesuatu seperti lembaran karet. Dengan tidak adanya materi, lembaran itu datar. Mulailah menjatuhkan bola di atasnya - bintang dan planet - dan lembarannya akan berubah bentuk. Bola berguling ke arah satu sama lain. Ketika benda bergerak, bentuk lembaran karet juga berubah sebagai respons.

Persamaan Einstein menggambarkan evolusi bentuk ruang-waktu. Anda memberi mereka informasi tentang kelengkungan dan energi di setiap titik, dan mereka memberikan bentuk ruang-waktu di masa depan. Dalam pengertian ini, persamaan Einstein mirip dengan persamaan apa pun yang mensimulasikan fenomena fisik: di sini bola berada pada titik nol, dan di sini - setelah lima detik.

"Ini adalah versi kuantitatif yang akurat secara matematis dari pernyataan bahwa ruang-waktu melengkung di hadapan materi," kata Peter Hinz, seorang peneliti di Clay Institute of Mathematics di University of California di Berkeley, yang bertanggung jawab atas hasil kedua dengan Andras Vasya.

Pada tahun 1916, hampir segera setelah rilis GTR, fisikawan Jerman Karl Schwarzschild menemukan solusi tepat untuk persamaan yang menggambarkan apa yang sekarang kita kenal dengan nama lubang hitam (istilah ini muncul hanya lima dekade kemudian ). Kemudian, fisikawan menemukan solusi tepat menggambarkan lubang hitam yang berputar dan BH dengan muatan listrik.

Dan ini semua adalah keputusan tepat yang menggambarkan BH. Jika Anda menambahkan setidaknya BH kedua, interaksi gaya menjadi sangat rumit untuk matematika modern sehingga hanya bisa digunakan dalam kasus yang sangat khusus.

Namun, kami masih dapat mengajukan pertanyaan penting tentang kelompok solusi terbatas ini. Satu pertanyaan seperti itu muncul pada tahun 1952 sebagai hasil karya ahli matematika Prancis Yvonne Choquet-Bruhat. Bahkan, kedengarannya seperti ini: apa yang terjadi jika Anda mengguncang lubang hitam?


Jika Anda mengguncang BH, itu akan menciptakan gelombang gravitasi. Untuk membuktikan stabilitas hipotesis sama dengan membuktikan bahwa gelombang-gelombang ini tersebar ke dalam kehampaan, seperti gelombang di permukaan kolam setelah batu jatuh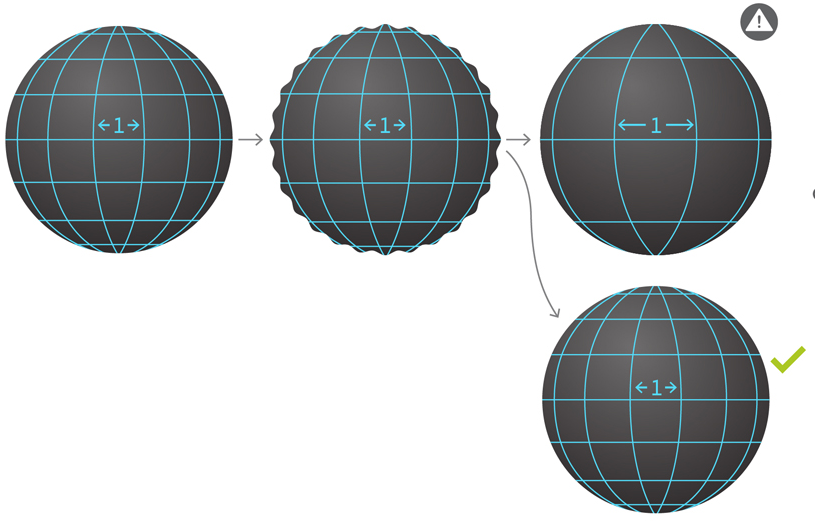


Ruang-waktu berubah seiring waktu, dan kisi yang digunakan untuk mengukur gelombang teredam berubah dengannya. Templat menentukan perubahan pada kisi, dan harus dipilih dengan benar. Misalkan kita memiliki ruang-waktu dengan grid 1 cm yang terkait dengan pola tertentu. Kami akan mengganggu ruang-waktu sehingga gelombang gravitasi muncul. Pola yang dipilih secara tidak tepat dapat menyebabkan jarak grid berubah, dan itu akan terlihat seperti gelombang tidak menipis. Pola yang tepat sangat penting untuk mengukur pengembalian ke keberlanjutan.

Masalah ini dikenal sebagai hipotesis stabilitas BH. Dia memperkirakan bahwa solusi untuk persamaan Einstein akan "stabil di bawah gangguan." Berbicara secara informal, jika Anda mengejutkan BH, maka ruang juga akan menjadi lebih mahal, dan kemudian di toga itu akan tenang dalam bentuk yang akan terlihat sangat mirip dengan apa yang kami mulai. "Secara kasar, keberlanjutan berarti bahwa jika kita mengambil solusi khusus dan membuat mereka sedikit marah, mengubah data, dinamika akhir akan sangat dekat dengan solusi asli," kata Kleinerman.

Yang disebut "stabilitas" adalah ujian penting dari teori fisik apa pun. Untuk memahami hal ini, akan bermanfaat untuk menyajikan contoh yang lebih akrab daripada BH.

Bayangkan sebuah kolam. Sekarang bayangkan Anda telah memberontak permukaannya dengan melemparkan batu ke sana. Kolam agak gelisah, dan kemudian akan tenang. Secara matematis, solusi dari persamaan yang digunakan untuk menggambarkan kolam (dalam hal ini, persamaan Navier-Stokes ) harus menggambarkan gambaran fisik dasar ini. Jika solusi awal tidak sesuai dengan keputusan di masa depan yang jauh, Anda mungkin bertanya-tanya tentang kebenaran persamaan Anda.

"Sebuah persamaan dapat memiliki sifat apa pun, dapat secara matematis benar, tetapi jika itu bertentangan dengan harapan fisik, itu tidak dapat benar," kata Vasya.


Peter Hinz, ahli matematika Universitas California

Untuk ahli matematika yang bekerja pada persamaan Einstein, bukti stabilitas bahkan lebih sulit ditemukan daripada solusi untuk persamaan itu sendiri. Pertimbangkan kasus ruang Minkowski datar - yang paling sederhana dari semua konfigurasi ruang-waktu. Solusi persamaan Einstein ini ditemukan pada tahun 1908, dalam konteks teori relativitas khusus Einstein sebelumnya. Tetapi hanya pada tahun 1993, matematikawan dapat membuktikan bahwa jika Anda mengguncang flat, ruang-waktu kosong, maka sekali lagi Anda mendapatkan ruang-waktu datar dan kosong. Hasil ini, diperoleh oleh Kleinermann dan Demetrios Christodoulou, adalah karya yang dihormati di bidang ini.

Salah satu kesulitan utama dengan bukti stabilitas terkait dengan pelacakan apa yang terjadi dalam ruang-waktu empat dimensi selama evolusi suatu solusi. Anda memerlukan sistem koordinat yang memungkinkan Anda mengukur jarak dan menentukan titik dalam ruang-waktu, seperti garis lintang dan bujur, yang digunakan untuk menentukan lokasi di Bumi. Tetapi tidak mudah untuk menemukan sistem koordinat yang bekerja di setiap titik dalam ruang waktu dan terus bekerja ketika bentuk ruang-waktu berubah.

"Kami tidak tahu cara untuk melakukan ini, cocok untuk semua kasus," kata Hinz dalam email. "Alam semesta tidak memberi kita sistem koordinat yang disukai."

Masalah pengukuran

Hal pertama yang harus dipahami tentang sistem koordinat adalah bahwa orang menciptakannya. Yang kedua - tidak setiap sistem koordinat memungkinkan Anda untuk menentukan semua titik dalam ruang.

Ambil lintang dan bujur: mereka dapat ditugaskan secara sewenang-wenang. Kartografer dapat memilih garis imajiner sebagai meridian utama. Dan meskipun lintang dan bujur membantu menentukan hampir semua tempat di Bumi, mereka tidak lagi masuk akal di kutub utara dan selatan. Jika Anda tidak tahu apa-apa tentang Bumi, dan hanya membaca garis lintang dan garis bujur di tangan Anda, Anda dapat salah menyimpulkan bahwa sesuatu yang secara topologi salah terjadi pada titik-titik ini.

Kemungkinan ini - untuk menarik kesimpulan yang salah tentang sifat-sifat ruang fisik karena tidak memadainya sistem koordinat yang menggambarkannya - adalah inti dari mengapa sangat sulit untuk membuktikan stabilitas ruang-waktu.

"Mungkin stabilitas ada, tetapi kami menggunakan koordinat yang tidak stabil, dan dengan demikian mengabaikan kebenaran stabilitas," kata Michalis Dafermos, seorang ahli matematika di University of Cambridge, seorang spesialis terkemuka dalam studi persamaan Einstein.

Dalam konteks teori stabilitas lubang hitam, sistem koordinat apa pun yang digunakan harus berkembang dengan cara yang sama seperti bentuk ruang-waktu - seperti sarung tangan yang nyaman beradaptasi dengan perubahan bentuk tangan. Korespondensi antara sistem koordinat dan ruang-waktu harus baik pada awalnya dan tetap baik sepanjang jalan. Jika tidak demikian, maka dua hal dapat terjadi yang mengganggu upaya untuk membuktikan keberadaan stabilitas.


Sergiu Kleinerman, Ahli Matematika Universitas Princeton

Pertama, sistem koordinat Anda dapat berubah bentuk, yang akan pecah pada titik-titik tertentu, seperti halnya lintang dan bujur yang berhenti bekerja di kutub. Poin semacam itu disebut "koordinat singularitas" (untuk membedakannya dari singularitas fisik, misalnya, lubang hitam). Ini adalah poin yang tidak terbatas dalam sistem koordinat yang tidak memungkinkan untuk sepenuhnya menggambarkan pengembangan solusi sampai akhir.

Kedua, sistem koordinat yang dipilih dengan buruk dapat menyembunyikan fenomena fisik yang harus diukur. Untuk membuktikan bahwa solusi persamaan Einstein datang ke keadaan tenang setelah perturbasi, matematikawan perlu memonitor riak ruang-waktu yang disebabkan oleh perturbasi. Untuk memahami mengapa ini perlu, ada baiknya kembali lagi ke analogi dengan kolam. Sebuah batu yang dilemparkan ke kolam menghasilkan gelombang. Stabilitas jangka panjang kolam berasal dari fakta bahwa gelombang melemah seiring waktu - mereka menjadi lebih kecil dan lebih kecil, sampai tidak ada jejak kehadiran mereka.

Situasinya mirip dengan ruang-waktu. Gangguan ini akan menyebabkan kaskade gelombang gravitasi, dan untuk membuktikan stabilitas perlu dibuktikan bahwa gelombang ini dilemahkan. Dan untuk ini, sistem koordinat, atau "grid", diperlukan untuk mengukur ukuran gelombang. Grid yang benar memungkinkan matematikawan untuk melihat bagaimana ombak rata dan akhirnya menghilang selamanya.

"Redaman perlu diukur relatif terhadap sesuatu, dan ini adalah di mana masalah grid masuk," kata Kleinerman. "Jika kita mengambil grid yang salah, maka bahkan jika ada stabilitas, ini tidak dapat dibuktikan, karena grid tidak akan menunjukkan padaku pelemahan." Dan jika Anda tidak menghitung laju pelemahan gelombang, tidak mungkin untuk membuktikan stabilitas. "

Masalahnya adalah bahwa meskipun sistem koordinat sangat penting, tidak jelas sistem mana yang harus dipilih. "Ada terlalu banyak kebebasan dalam memilih kondisi untuk grid ini," kata Hinz. "Dan sebagian besar opsi ternyata salah."

Dalam perjalanan ke tujuan

Bukti lengkap dari stabilitas lubang hitam membutuhkan bukti bahwa semua solusi persamaan Einstein untuk BH yang diketahui (dengan putaran lubang hitam dalam batas-batas tertentu) stabil setelah gangguan. Di antara solusi yang terkenal adalah solusi Schwarzschild yang menggambarkan ruang-waktu dari BH yang tidak berputar, dan keluarga Kerr dari solusi yang menggambarkan konfigurasi ruang-waktu di mana tidak ada yang lain selain satu BH yang berputar (dan sifat-sifat BH ini - momentum massa dan sudut - berbeda dalam keluarga solusi) .

Kedua hasil baru sebagian maju ke arah bukti hipotesis lengkap.

Hinz dan Washi, dalam sebuah makalah yang diterbitkan di arxiv.org pada 2016, membuktikan bahwa lubang hitam yang berputar perlahan stabil. Tetapi pekerjaan mereka tidak mencakup BH yang berputar dengan kecepatan lebih besar dari batas tertentu.

Juga, bukti mereka memiliki beberapa asumsi tentang sifat ruang-waktu. Hipotesis asli terjadi di ruang Minkowski, yang tidak hanya datar dan kosong, tetapi juga memiliki ukuran tertentu. Bukti dari Hintz dan Vasya terjadi di ruang de Sitter, di mana ruang-waktu dengan percepatan tumbuh keluar, seperti di Alam Semesta yang sebenarnya. Mengubah pemandangan menyederhanakan masalah dari sudut pandang teknis, dan ini dapat dipahami dengan analogi: jika Anda melempar batu ke kolam yang mengembang, ekspansi akan meregangkan ombak dan mereka akan melemah lebih cepat daripada jika kolam tidak mengembang.

"Kami melihat alam semesta dengan ekspansi yang dipercepat," kata Hinz. "Itu membuat tugas sedikit lebih mudah, karena proses ini mencairkan gelombang gravitasi."

Kleinermann dan Scheftel memiliki fitur yang sedikit berbeda. Buktinya, bagian pertama dari yang diterbitkan November lalu, terjadi di ruang-waktu Schwarzschild - yang lebih dekat dengan kondisi asli, masalah yang lebih kompleks. Mereka membuktikan stabilitas BH yang tidak berputar, tetapi tidak memperhatikan keputusan yang diputar. Selain itu, mereka membuktikan stabilitas BH hanya untuk kelas gangguan yang sempit - gelombang-gelombang gravitasi yang dihasilkan simetris dengan cara tertentu.

Kedua hasil menyajikan teknik baru untuk memilih sistem koordinat yang sesuai. Hinz dan Vasi mulai dengan solusi perkiraan persamaan berdasarkan pada sistem koordinat perkiraan, dan secara bertahap meningkatkan keakuratan jawaban, sampai mereka datang ke solusi yang tepat dan koordinat yang berperilaku baik. Kleinerman dan Scheftel menggunakan pendekatan yang lebih geometris.

Sekarang kedua tim berusaha membangun bukti hipotesis lengkap berdasarkan metode mereka. Beberapa ahli pengamat percaya bahwa hari ini tidak jauh.

"Saya benar-benar percaya bahwa sekarang semuanya berada pada tahap kesulitan teknis," kata Dafermos. "Ternyata untuk menyelesaikan masalah ini, ide-ide baru tidak lagi diperlukan." Dia menekankan bahwa bukti akhir dapat ditawarkan oleh salah satu ahli matematika yang sedang mengerjakan masalah saat ini.

Selama seratus tahun, persamaan Einstein berfungsi sebagai instruksi eksperimental yang dapat diandalkan untuk Semesta. Sekarang ahli matematika mungkin semakin dekat untuk menunjukkan mengapa mereka bekerja dengan baik.