Terjemahan dari Bagaimana Mesin Masuk Akal dengan Big Data: Pengantar Algoritma Clustering .Lihatlah gambar di bawah ini. Ini adalah kumpulan serangga (siput bukan serangga, tetapi kami tidak akan menemukan kesalahan) dari berbagai bentuk dan ukuran. Sekarang bagilah mereka menjadi beberapa kelompok sesuai dengan tingkat kesamaannya. Tanpa tangkapan. Mulailah dengan mengelompokkan laba-laba.
Jadi? Meskipun tidak ada solusi "benar" di sini, Anda harus membagi makhluk-makhluk ini menjadi empat
kelompok . Dalam satu kelompok terdapat laba-laba, di kelompok kedua - sepasang siput, di kelompok ketiga - kupu-kupu, dan di kelompok keempat - trio lebah dan tawon.
Bagus, kan? Anda mungkin bisa melakukan hal yang sama jika ada dua kali lebih banyak serangga dalam gambar. Dan jika Anda punya banyak waktu - atau keinginan untuk entomologi - maka Anda mungkin akan mengelompokkan ratusan serangga.
Namun, untuk sebuah mesin, pengelompokan sepuluh objek ke dalam kelompok yang berarti bukanlah tugas yang mudah. Berkat cabang matematika yang rumit seperti
kombinatorik , kita tahu bahwa 10 serangga dikelompokkan dalam 115.975 cara. Dan jika ada 20 serangga, maka jumlah opsi pengelompokan
akan melebihi 50 triliun .
Dengan seratus serangga, jumlah solusi yang mungkin akan lebih besar dari
jumlah partikel elementer di Alam Semesta yang diketahui . Berapa banyak lagi Menurut perkiraan saya, sekitar
lima ratus juta miliar miliar kali lebih . Ternyata lebih dari
empat juta miliar solusi
google (
apa itu google? ). Dan ini hanya untuk ratusan objek.
Hampir semua kombinasi ini tidak ada artinya. Meskipun ada sejumlah solusi yang tak terbayangkan, Anda sendiri dengan cepat menemukan salah satu dari beberapa cara pengelompokan yang bermanfaat.
Kami manusia menerima begitu saja kemampuan kami yang luar biasa untuk membuat katalog dan memahami sejumlah besar data. Tidak masalah apakah itu teks, atau gambar di layar, atau urutan objek - orang, secara umum, secara efektif memahami data yang berasal dari dunia sekitarnya.
Mengingat bahwa aspek kunci dari pengembangan AI dan pembelajaran mesin adalah bahwa mesin dapat dengan cepat memahami volume besar data input, bagaimana saya dapat meningkatkan efisiensi kerja? Pada artikel ini, kami akan mempertimbangkan tiga algoritma pengelompokan dengan mesin yang dapat dengan cepat memahami sejumlah besar data. Daftar ini jauh dari lengkap - ada algoritma lain - tetapi sudah sangat mungkin untuk memulainya.
Untuk setiap algoritma, saya akan menjelaskan kapan itu dapat digunakan, cara kerjanya, dan saya juga akan memberikan contoh dengan analisis langkah demi langkah. Saya percaya bahwa untuk memahami algoritma yang sebenarnya, Anda perlu mengulangi kerjanya sendiri. Jika Anda
benar -
benar tertarik , Anda akan menyadari bahwa yang terbaik adalah menjalankan algoritma di atas kertas. Bertindak, tidak ada yang akan menyalahkan Anda!
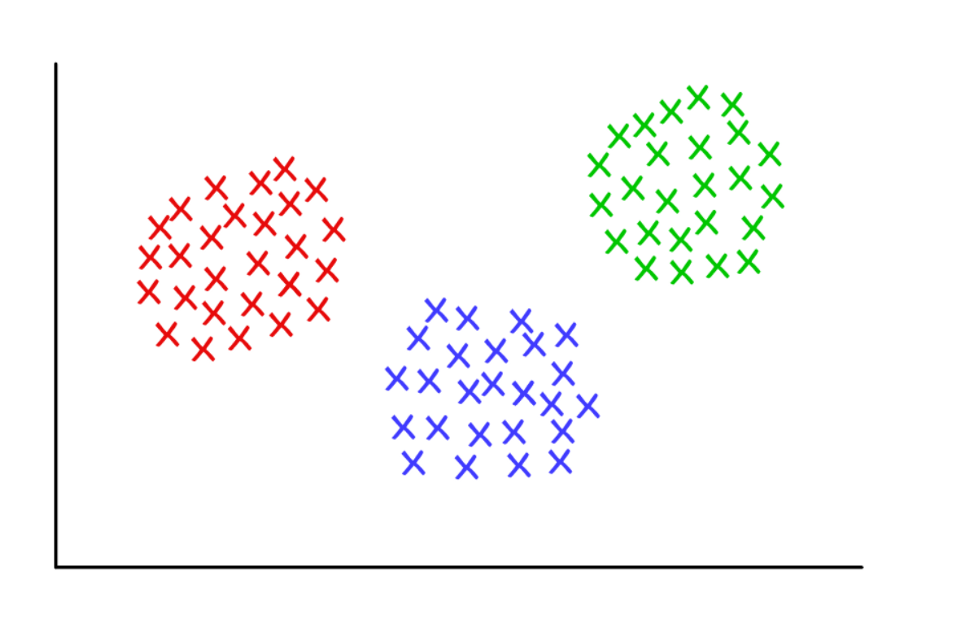Tiga cluster yang mencurigakan rapi dengan k = 3K-means clustering
Digunakan oleh:
Ketika Anda memahami berapa banyak kelompok dapat diperoleh untuk menemukan
yang telah ditentukan (apriori).
Cara kerjanya:
Algoritma secara acak menetapkan setiap pengamatan ke salah satu kategori
k , dan kemudian menghitung
rata -
rata untuk setiap kategori. Kemudian ia menugaskan kembali setiap pengamatan ke kategori dengan rata-rata terdekat, dan kembali menghitung rata-rata. Proses ini diulang sampai penugasan kembali diperlukan.
Contoh kerja:
Ambil grup yang terdiri dari 12 pemain dan jumlah gol yang dicetak oleh mereka masing-masing di musim ini (misalnya, dalam kisaran 3 hingga 30). Kami membagi para pemain, katakanlah, menjadi tiga kelompok.
Langkah 1 : Anda perlu membagi pemain secara acak menjadi tiga kelompok dan menghitung rata-rata untuk masing-masing pemain.
Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16
Langkah 2 : menetapkan kembali setiap pemain ke grup dengan rata-rata terdekat. Misalnya, pemain A (5 gol) masuk ke grup 2 (rata-rata = 9). Kemudian kami menghitung rata-rata grup.
Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21
Ulangi langkah 2 lagi dan lagi sampai para pemain berhenti berganti kelompok. Dalam contoh buatan ini, ini akan terjadi pada iterasi berikutnya.
Hentikan itu! Anda telah membentuk tiga kelompok dari set data!
Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23
Cluster harus sesuai dengan posisi pemain di lapangan - bek, bek tengah dan ke depan. K-means berfungsi dalam contoh ini karena ada alasan untuk percaya bahwa data akan dibagi ke dalam tiga kategori ini.
Dengan demikian, berdasarkan variasi statistik dalam kinerja, mesin dapat membenarkan lokasi pemain di lapangan untuk olahraga tim apa pun. Ini berguna untuk analitik olahraga, juga untuk tugas-tugas lain di mana membagi dataset ke dalam kelompok yang telah ditentukan membantu untuk menarik kesimpulan yang tepat.
Ada beberapa variasi dari algoritma yang dijelaskan. Pembentukan awal cluster dapat dilakukan dengan berbagai cara. Kami memeriksa klasifikasi acak pemain ke dalam kelompok, diikuti oleh perhitungan rata-rata. Akibatnya, rata-rata kelompok awal dekat satu sama lain, yang meningkatkan pengulangan.
Pendekatan alternatif adalah membentuk kelompok yang hanya terdiri dari satu pemain, dan kemudian mengelompokkan pemain ke dalam kelompok terdekat. Cluster yang dihasilkan lebih tergantung pada tahap awal pembentukan, dan pengulangan dalam dataset dengan variabilitas tinggi menurun. Tetapi dengan pendekatan ini, mungkin diperlukan lebih sedikit iterasi untuk menyelesaikan algoritme, karena lebih sedikit waktu akan dihabiskan untuk memisahkan grup.
Kelemahan yang jelas dari pengelompokan k-means adalah bahwa Anda perlu menebak
sebelumnya berapa banyak cluster yang Anda miliki. Ada metode untuk menilai kesesuaian satu set cluster tertentu. Sebagai contoh, Sum-of-Squares Dalam-Cluster adalah ukuran variabilitas dalam setiap cluster. Semakin baik cluster, semakin rendah jumlah total intracluster kuadrat.
Pengelompokan hierarkis
Digunakan oleh:
Saat Anda perlu mengungkap hubungan antara nilai-nilai (pengamatan).
Cara kerjanya:
Matriks jarak dihitung di mana nilai sel (
i, j ) adalah metrik jarak antara nilai-nilai
i dan
j . Kemudian sepasang nilai terdekat diambil dan rata-rata dihitung. Matriks jarak baru dibuat, nilai-nilai berpasangan digabungkan menjadi satu objek. Kemudian sepasang nilai terdekat diambil dari matriks baru ini dan nilai rata-rata baru dihitung. Siklus berulang sampai semua nilai dikelompokkan.
Contoh kerja:
Ambil dataset yang sangat sederhana dengan beberapa spesies paus dan lumba-lumba. Saya seorang ahli biologi, dan saya dapat meyakinkan Anda bahwa lebih banyak properti digunakan untuk membangun
pohon filogenetik . Tetapi untuk contoh kita, kita membatasi diri pada panjang tubuh karakteristik enam spesies mamalia laut. Akan ada dua tahap perhitungan.
Langkah 1 : matriks jarak antara semua tampilan dihitung. Kami akan menggunakan metrik Euclidean yang menggambarkan seberapa jauh data kami satu sama lain, seperti pemukiman di peta. Anda bisa mendapatkan perbedaan panjang tubuh masing-masing pasangan dengan membaca nilai di persimpangan kolom dan baris yang sesuai.
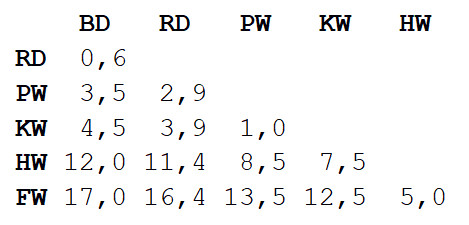Langkah 2 : Ambil sepasang dua spesies yang paling dekat satu sama lain. Dalam hal ini, itu adalah lumba-lumba hidung botol dan lumba-lumba abu-abu, di mana panjang tubuh rata-rata adalah 3,3 m.
Kami ulangi langkah 1, sekali lagi menghitung matriks jarak, tetapi kali ini kami menggabungkan dolphin bottlenose dan gray dolphin menjadi satu objek dengan panjang tubuh 3,3 m.
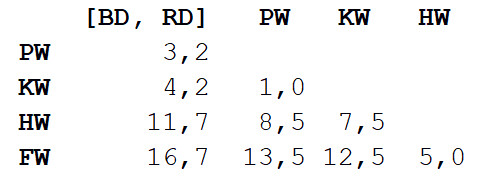
Sekarang kita ulangi langkah 2, tetapi dengan matriks jarak baru. Kali ini paus penggiling dan pembunuh akan menjadi yang terdekat, jadi mari kita taruh dalam pasangan dan hitung rata-rata - 7 m.
Selanjutnya, ulangi langkah 1: sekali lagi, hitung matriks jarak, tetapi dengan paus penggiling dan pembunuh dalam bentuk objek tunggal dengan panjang tubuh 7 m.
Ulangi langkah 2 dengan matriks ini. Jarak terkecil (3,7 m) akan berada di antara dua objek gabungan, jadi kami akan menggabungkannya menjadi objek yang lebih besar dan menghitung nilai rata-rata - 5,2 m.
Kemudian ulangi langkah 1 dan hitung matriks baru dengan menggabungkan lumba-lumba hidung botol / lumba-lumba abu-abu dengan paus giling / pembunuh.
Ulangi langkah 2. Jarak terkecil (5 m) akan berada di antara humpback dan finwale, jadi kami menggabungkannya dan menghitung rata-rata - 17,5 m.
Sekali lagi langkah 1: hitung matriksnya.
Terakhir, ulangi langkah 2 - hanya ada satu jarak yang tersisa (12,3 m), jadi kami akan menyatukan semua orang menjadi satu objek dan berhenti. Inilah yang terjadi:
[[[BD, RD],[PW, KW]],[HW, FW]]
Objek memiliki struktur hierarkis (ingat
JSON ), sehingga dapat ditampilkan sebagai grafik pohon, atau dendrogram. Hasilnya mirip dengan silsilah keluarga. Semakin dekat dua nilai pada pohon, semakin banyak kesamaan atau semakin erat hubungannya.
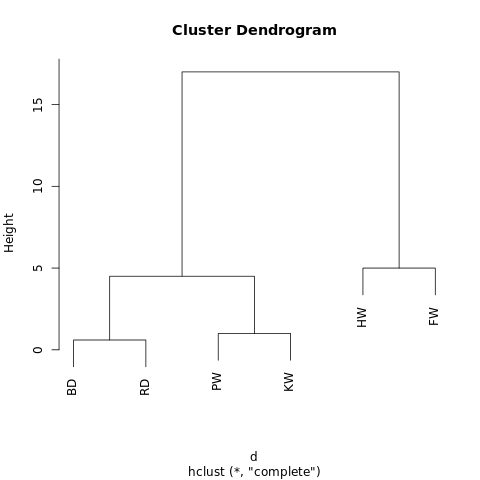Program sederhana yang dibuat menggunakan R-Fiddle.orgStruktur dendrogram memungkinkan Anda untuk memahami struktur dataset itu sendiri. Dalam contoh kami, kami mendapat dua cabang utama - satu dengan humpback dan finwal, yang lain dengan lumba-lumba hidung botol / lumba-lumba abu-abu dan paus giling / pembunuh.
Dalam biologi evolusi, kumpulan data yang jauh lebih besar dengan banyak spesies dan banyak karakter digunakan untuk mengidentifikasi hubungan taksonomi. Di luar biologi, pengelompokan hierarkis diterapkan di bidang Penambangan Data dan pembelajaran mesin.
Pendekatan ini tidak memerlukan prediksi jumlah cluster yang diperlukan. Anda dapat membagi dendrogram yang dihasilkan menjadi kelompok-kelompok, “memotong” pohon pada ketinggian yang diinginkan. Anda dapat memilih ketinggian dengan berbagai cara, tergantung pada resolusi pengelompokan data yang diinginkan.
Misalnya, jika dendrogram di atas terputus pada ketinggian 10, maka kita akan memotong dua cabang utama, sehingga membagi dendrogram menjadi dua kolom. Jika dipotong pada ketinggian 2, maka bagilah dendrogram menjadi tiga kelompok.
Algoritma pengelompokan hierarkis lainnya mungkin berbeda dalam tiga aspek dari yang dijelaskan dalam artikel ini.
Yang paling penting adalah pendekatannya. Di sini kami menggunakan metode
aglomerasi : kami mulai dengan nilai-nilai individual dan mengelompokkannya secara siklis hingga kami mendapatkan satu kelompok besar. Pendekatan alternatif (dan lebih kompleks secara komputasional) menyiratkan urutan terbalik: pertama satu cluster besar dibuat, dan kemudian secara berurutan dibagi menjadi kelompok yang lebih kecil sampai nilai-nilai terpisah tetap.
Ada juga beberapa metode untuk menghitung matriks jarak. Metrik Euclidean cukup untuk sebagian besar tugas, tetapi
metrik lainnya lebih cocok dalam beberapa situasi.
Akhirnya, kriteria keterkaitan dapat bervariasi. Hubungan antara cluster tergantung pada kedekatan mereka satu sama lain, tetapi definisi "kedekatan" bisa berbeda. Dalam contoh kami, kami mengukur jarak antara nilai rata-rata (atau "centroid") dari masing-masing kelompok dan menggabungkan kelompok terdekat berpasangan. Tetapi Anda dapat menggunakan definisi lain.
Misalkan setiap cluster terdiri dari beberapa nilai diskrit. Jarak antara dua cluster dapat didefinisikan sebagai jarak minimum (atau maksimum) antara salah satu nilainya, seperti yang ditunjukkan di bawah ini. Untuk konteks yang berbeda, akan lebih mudah untuk menggunakan definisi kriteria join yang berbeda.
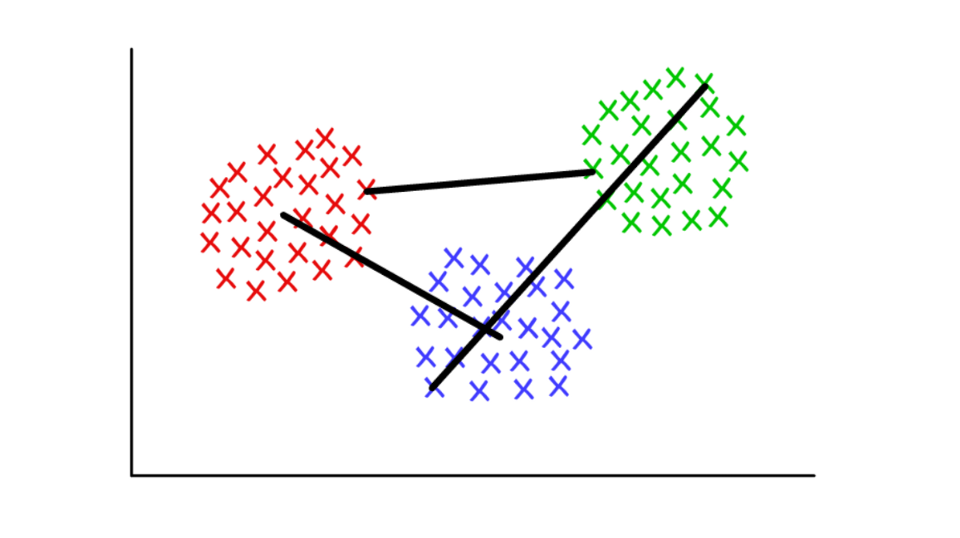Merah / biru: kolam centroid; merah / hijau: menggabungkan berdasarkan minima; hijau / biru: penggabungan berdasarkan tertinggi.Definisi komunitas dalam grafik (Grafik Deteksi Komunitas)
Digunakan oleh:
Ketika data Anda dapat disajikan dalam bentuk jaringan, atau "grafik".
Cara kerjanya:
Komunitas dalam grafik dapat secara kasar didefinisikan sebagai subset dari simpul yang lebih terhubung satu sama lain daripada ke seluruh jaringan. Ada berbagai algoritma definisi komunitas berdasarkan definisi yang lebih spesifik, seperti Edge Betweenness, Modularity-Maximsation, Walktrap, Clique Percolation, Leading Eigenvector ...
Contoh kerja:
Teori grafik adalah cabang matematika yang sangat menarik yang memungkinkan kita untuk memodelkan sistem yang kompleks dalam bentuk set abstrak "titik" (simpul, simpul) yang dihubungkan oleh "garis" (tepi).
Mungkin aplikasi pertama dari grafik yang muncul di pikiran adalah studi tentang jejaring sosial. Dalam hal ini, puncak mewakili orang-orang yang terhubung dengan tulang rusuk ke teman / pelanggan. Tetapi Anda dapat membayangkan sistem apa pun dalam bentuk jaringan jika Anda dapat membenarkan metode koneksi komponen yang bermakna. Aplikasi inovatif pengelompokan menggunakan teori grafik termasuk mengekstraksi properti dari data visual dan menganalisis jaringan regulasi genetik.
Sebagai contoh sederhana, mari kita lihat grafik di bawah ini. Ini menunjukkan delapan situs yang paling sering saya kunjungi. Tautan di antara mereka didasarkan pada tautan dalam artikel Wikipedia. Data semacam itu dapat dikumpulkan secara manual, tetapi untuk proyek besar jauh lebih cepat untuk menulis skrip Python. Misalnya, ini:
https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .
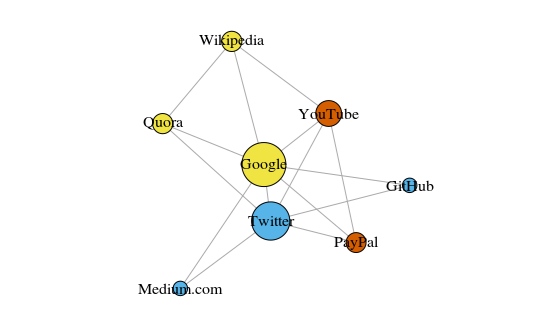Grafik dibuat menggunakan paket igraph untuk R 3.3.3Warna puncak tergantung pada partisipasi dalam masyarakat, dan ukurannya tergantung pada sentralitas. Harap dicatat bahwa yang paling utama adalah Google dan Twitter.
Juga, cluster yang dihasilkan sangat akurat mencerminkan tugas nyata (ini selalu merupakan indikator kinerja yang penting). Vertikal yang mewakili situs tautan / pencarian disorot dengan warna kuning; situs yang disorot biru untuk publikasi online (artikel, tweet, atau kode); yang disorot dengan warna merah adalah PayPal dan YouTube, yang didirikan oleh mantan karyawan PayPal. Pengurangan yang bagus untuk komputer!
Selain memvisualisasikan sistem besar, kekuatan sebenarnya dari jaringan terletak pada analisis matematika. Mari kita mulai dengan mengubah gambar jaringan menjadi format matematika. Berikut
ini adalah matriks
kedekatan dari jaringan.
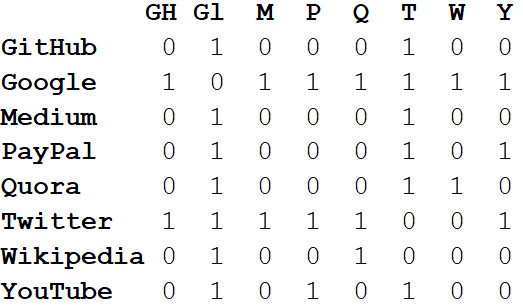
Nilai-nilai di persimpangan kolom dan baris menunjukkan apakah ada tepi antara pasangan simpul ini. Misalnya, antara Medium dan Twitter, maka, di persimpangan baris dan kolom ini berdiri 1. Dan antara Medium dan PayPal tidak ada tepi, jadi di sel yang sesuai ada 0.
Jika kami mewakili semua properti jaringan dalam bentuk matriks adjacency, ini akan memungkinkan kami untuk menarik semua jenis kesimpulan yang berguna. Misalnya, jumlah nilai dalam kolom atau baris apa pun mencirikan
tingkat setiap titik - yaitu, jumlah objek yang terhubung ke titik ini. Biasanya ditunjukkan dengan huruf
k .
Jika kita menjumlahkan derajat semua simpul dan membaginya menjadi dua, kita mendapatkan L - jumlah tepi dalam jaringan. Dan jumlah baris dan kolom sama dengan N - jumlah simpul dalam jaringan.
Mengetahui hanya k, L, N dan nilai-nilai dalam semua sel dari matriks adjacency A, kita dapat menghitung modularitas dari setiap pengelompokan.
Misalkan kita telah mengelompokkan jaringan ke sejumlah komunitas. Kemudian Anda dapat menggunakan nilai modularitas untuk memprediksi "kualitas" pengelompokan. Modularitas yang lebih tinggi menunjukkan bahwa kami membagi jaringan menjadi komunitas "tepat", dan modularitas yang lebih rendah menunjukkan bahwa cluster dibentuk lebih secara kebetulan daripada secara wajar. Untuk membuatnya lebih jelas:
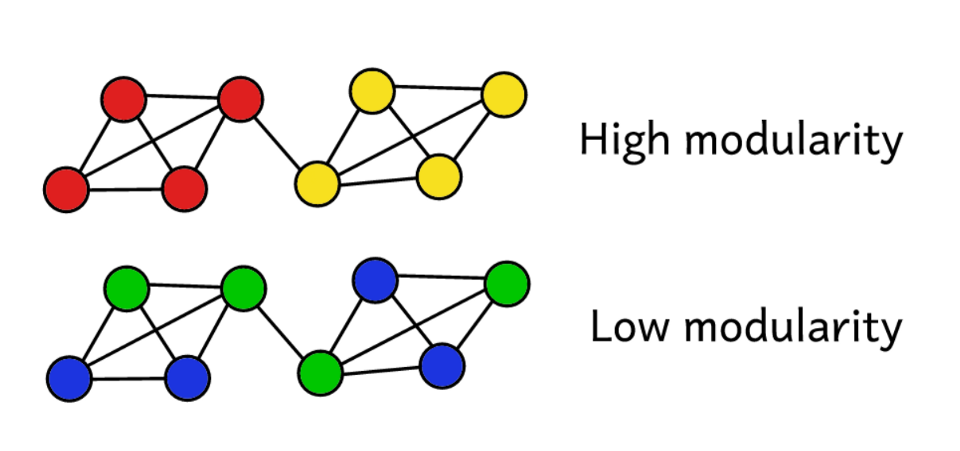
Modularitas berfungsi sebagai tolok ukur “kualitas” kelompok.
Modularitas dapat dihitung menggunakan rumus berikut:
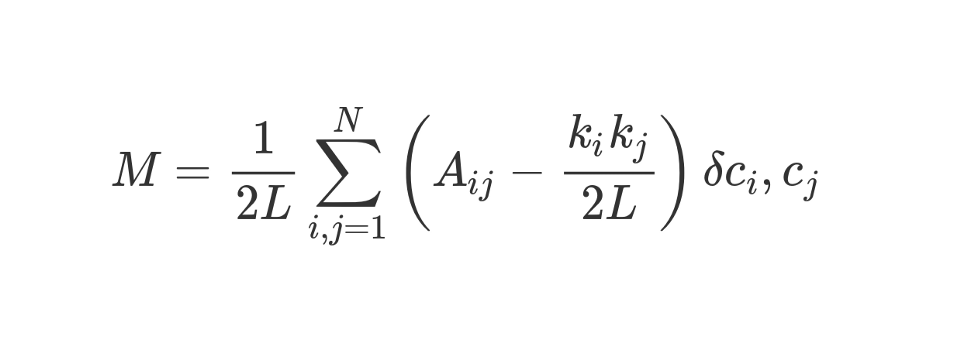
Mari kita lihat formula yang tampak luar biasa ini.
M , seperti yang Anda tahu, ini adalah modularitas.
Koefisien
1 / 2L berarti bahwa kita membagi sisa "tubuh" rumus dengan 2L, yaitu, dengan jumlah ganda sisi dalam jaringan. Dengan Python, orang bisa menulis:
sum = 0 for i in range(1,N): for j in range(1,N): ans =
Apa itu
#stuff with i and j ? Bit dalam tanda kurung memberitahu kita untuk mengurangi (k_i k_j) / 2L dari A_ij, di mana A_ij adalah nilai dalam matriks di persimpangan baris i dan kolom j.
Nilai k_i dan k_j adalah derajat masing-masing simpul. Mereka dapat ditemukan dengan menjumlahkan nilai dalam baris i dan kolom j, masing-masing. Jika kita mengalikannya dan membaginya dengan 2L, maka kita mendapatkan jumlah tepi yang diharapkan antara simpul i dan j jika jaringan dicampur secara acak.
Isi kurung mencerminkan perbedaan antara struktur aktual jaringan dan yang diharapkan jika jaringan dibangun kembali secara acak. Jika Anda bermain-main dengan nilai-nilai, maka modularitas tertinggi akan berada di A_ij = 1 dan rendah (k_i k_j) / 2L. Yaitu, modularitas meningkat jika ada tepi “tak terduga” antara simpul i dan j.
Akhirnya, kita mengalikan isi tanda kurung dengan apa yang ditunjukkan dalam rumus sebagai δc_i, c_j. Ini adalah fungsi Kronecker-delta. Berikut ini implementasinya dalam Python:
def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A")
Ya, sangat sederhana. Fungsi ini mengambil dua argumen, dan jika keduanya identik, ia mengembalikan 1, dan jika tidak, maka 0.
Dengan kata lain, jika simpul i dan j jatuh ke satu cluster, maka δc_i, c_j = 1. Dan jika mereka berada di cluster yang berbeda, fungsi akan mengembalikan 0.
Karena kita mengalikan isi tanda kurung dengan simbol Kronecker, hasil dari jumlah yang diinvestasikan
Σ akan menjadi yang tertinggi ketika simpul di dalam satu kluster dihubungkan oleh sejumlah besar tepi "tak terduga". Dengan demikian, modularitas adalah indikator seberapa baik grafik dikelompokkan ke dalam komunitas individu.
Division by 2L membatasi modularitas atas menjadi satu. Jika modularitas mendekati 0 atau negatif, ini berarti bahwa pengelompokan jaringan saat ini tidak masuk akal. Dengan meningkatkan modularitas, kita dapat menemukan cara yang lebih baik untuk mengelompokkan jaringan.
Harap perhatikan bahwa untuk mengevaluasi "kualitas" pengelompokan grafik, kita harus menentukan terlebih dahulu bagaimana pengelompokannya. Sayangnya, kecuali sampelnya sangat kecil, karena kompleksitas komputasinya, secara fisik tidak mungkin untuk dengan bodohnya melewati semua metode pengelompokan grafik dengan membandingkan modularitasnya.
Combinatorics menunjukkan bahwa untuk jaringan dengan 8 simpul, ada 4.140 metode pengelompokan. Untuk jaringan dengan 16 simpul, sudah ada lebih dari 10 miliar cara, untuk jaringan dengan 32 simpul - 128 septillion, dan untuk jaringan dengan 80 simpul jumlah metode pengelompokan akan melebihi
jumlah atom di alam semesta yang dapat diamati .
Oleh karena itu, alih-alih pencacahan, kami akan menggunakan metode heuristik, yang akan membantu menghitung cluster dengan relatif mudah dengan modularitas maksimum. Ini adalah suatu algoritma yang disebut
Fast-Greedy Modularity-Maximization , semacam analog dengan algoritma pengelompokan hierarkis aglomeratif yang dijelaskan di atas. Alih-alih menggabungkan berdasarkan kedekatan, Mod-Max menyatukan komunitas tergantung pada perubahan modularitas. Cara kerjanya:
Pertama, setiap simpul ditugaskan ke komunitasnya sendiri dan modularitas seluruh jaringan dihitung - M.
Langkah 1 : untuk setiap pasangan komunitas yang terhubung oleh setidaknya satu sisi, algoritma menghitung perubahan yang dihasilkan dalam modularitas ΔM dalam hal menggabungkan pasangan komunitas ini.
Langkah 2 : lalu pasangan diambil, saat dikombinasikan, ΔM akan maksimal, dan dikombinasikan. Untuk pengelompokan ini, modularitas baru dihitung dan disimpan.
Langkah 1 dan 2
diulang : setiap kali sepasang komunitas bergabung, yang memberikan ΔM terbesar, skema pengelompokan baru dan M.
Iterasi
berhenti ketika semua simpul dikelompokkan menjadi satu kelompok besar. Sekarang algoritma memeriksa catatan yang disimpan dan menemukan skema pengelompokan dengan modularitas tertinggi. Dialah yang kembali sebagai struktur komunitas.
Secara komputasi itu sulit, setidaknya untuk manusia. Teori grafik adalah sumber yang kaya akan masalah komputasi yang sulit dan masalah NP-hard. Dengan menggunakan grafik, kita dapat menarik banyak kesimpulan yang berguna tentang sistem dan dataset yang kompleks. Tanyakan Larry Page, yang algoritme PageRanknya - yang membantu Google mengubah dari permulaan menjadi dominan global dalam waktu kurang dari satu generasi - seluruhnya didasarkan pada teori grafik.
Studi tentang teori grafik saat ini fokus pada identifikasi komunitas. Ada banyak alternatif untuk algoritma Modularity-Maximization, yang, meskipun bermanfaat, bukan tanpa kekurangannya.
Pertama, dengan pendekatan aglomerasi, komunitas kecil dan terdefinisi dengan baik sering digabungkan menjadi komunitas yang lebih besar. Ini disebut batas resolusi - algoritma tidak mengalokasikan komunitas yang lebih kecil dari ukuran tertentu. Kelemahan lain adalah bahwa alih-alih satu puncak global yang diucapkan dan mudah dicapai, algoritma Mod-Max berupaya menghasilkan "dataran tinggi" yang luas dari banyak nilai modularitas yang dekat. Akibatnya, sulit untuk menentukan pemenang.
Algoritme lain menggunakan metode yang berbeda untuk mendefinisikan komunitas. Sebagai contoh, Edge-Betweenness adalah algoritma yang memecah (memecah) yang dimulai dengan mengelompokkan semua simpul menjadi satu kelompok besar. Kemudian ujung-ujung "paling penting" dihilangkan secara iteratif sampai semua simpul diisolasi. Hasilnya adalah struktur hierarkis di mana simpul lebih dekat satu sama lain, semakin mirip.
Algoritma, Clique Percolation, memperhitungkan kemungkinan persimpangan antara komunitas. Ada sekelompok algoritma berdasarkan
random walk pada grafik, dan ada metode
pengelompokan spektral yang berhubungan dengan dekomposisi spektral (eigendecomposition) dari matriks adjacency dan matriks lain yang diturunkan darinya. Semua ide ini digunakan untuk menyorot fitur, misalnya, dalam visi mesin.
Kami tidak akan menganalisis contoh kerja untuk setiap algoritma secara detail.
Cukuplah untuk mengatakan bahwa penelitian aktif saat ini sedang dilakukan dalam arah ini dan teknik analisis data yang kuat sedang dibuat, yang sangat sulit untuk dihitung 20 tahun yang lalu.Kesimpulan
, - , , . , , 20-40 .
, — , . , , .
, , , , . , - , , ? - !