Sebuah artikel tentang analisis permainan oleh jaringan perdagangan terkenal membangkitkan minat
besar pada
Cloud4Y . Berikut adalah beberapa bagian untuk mempercepat Anda:
Suatu hari, pada pagi musim semi yang cerah, membaca forum kota, saya menemukan tautan dengan permainan sederhana dari jaringan perdagangan terkenal. Permainan (aksi) yang didedikasikan untuk Piala Dunia adalah lapangan tiga demi tiga yang tidak rumit diisi dengan bola sepak. Dengan mengklik bola, kami membuka gambar dengan produk tertentu. Saat membuka tiga gambar yang identik, peserta dijamin mendapat tanda terima gratis produk ini di salah satu toko jaringan. Juga, di bawah salah satu bola ada gambar kartu merah, pembukaan yang berarti akhir pertandingan.
Penulis artikel itu mulai menyelidiki alasan kehilangannya dan, berdasarkan hasil perhitungan, menemukan yang berikut:
Sketsa cepat formula pada serbet, dan ternyata probabilitas menang adalah 1/4. Untuk 5 bidang, saya harus mengotak-atik, tetapi probabilitas yang dihitung juga 25%.
...
Menjalankan skrip, saya mendapat hasil yang tidak terduga - 25% dari kemenangan. Setelah bermain dengan jumlah elemen yang menang dan jumlah total field, saya menemukan bahwa probabilitas menang dalam permainan seperti itu tidak tergantung pada jumlah field dan sama dengan satu dibagi dengan jumlah elemen yang menang bertambah satu.
Kami tertarik pada kebenaran perhitungan seperti itu dan, menggantikan serbet dengan Excel, kami mulai bekerja mencari kebenaran matematika. Pembaca yang menyukai teori probabilitas diundang ke kucing, untuk memverifikasi kebenaran perhitungan kami.
Pertama-tama, kami mencari tahu aturan mainnya. Dalam hal ini, tanpa menyadarinya, pengguna Habr
Stecenko membantu dalam
komentarnya . Ia juga menulis:
Jika Anda melihat skrip penulis, itu ditulis dengan asumsi bahwa HARUS ada tiga kartu dari satu produk di lapangan, satu kartu berisi lima barang lain, dan satu kartu merah, sedangkan deskripsi permainannya sama sekali tidak mengikuti ini - aturannya tidak mengatakan bahwa kombinasi yang menang harus ada di lapangan.
Namun, peraturan mengatakan bahwa total 26 produk terlibat. Ternyata penerbitan 9 kartu dihasilkan: 8 kartu adalah kombinasi dari 26 produk dengan pengulangan, dan satu kartu berwarna merah.
Dalam kondisi seperti itu, perhitungan probabilitas matematika untuk menang agak lebih rumit daripada yang disarankan penulis asli. Gim ini terdiri dari beberapa lapisan:- Peluang membuka kartu N tanpa membuka kartu merah adalah probabilitas durasi permainan yang berbeda, terlepas dari apakah akan ada hadiah.
- Probabilitas mengumpulkan kombinasi 3 kartu dengan barang yang sama. Probabilitas ini bervariasi dengan durasi permainan yang berbeda. Penting untuk dipahami bahwa satu set 8 kartu dengan barang dan selalu satu kartu merah tidak harus mengandung setidaknya satu pasang kartu yang identik, belum lagi tiga kartu sekaligus.
Mari kita mulai dengan yang sederhana - memahami bagaimana jumlah peserta akan berkurang dengan peningkatan jumlah kartu yang mereka buka karena aturan kartu merah.
Peluang dengan panjang gim yang berbeda
Kami menghitung seberapa besar kemungkinan untuk uji coba N (kartu terbuka) merah akan dibuka.UPD: Awalnya, kami menghitung probabilitas pembukaan merah menggunakan distribusi binomial. Ini tidak menjamin kami benar-benar 1 kartu merah, dengan distribusi seperti itu kemungkinan besar ada satu kartu merah, tetapi mungkin ada 0 atau seluruhnya 9 dengan probabilitas yang sangat, sangat kecil. Sekali lagi, terima kasih kepada Stecenko karena menunjukkan kesalahan dalam komentar dan menyarankan solusi yang tepat .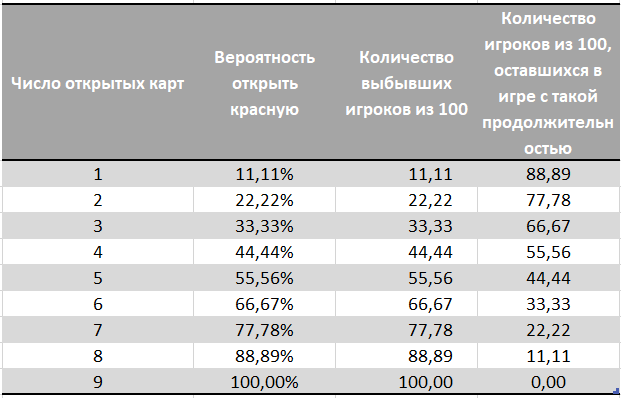
Kolom terakhir menunjukkan berapa banyak pemain dari seratus yang tersisa dalam permainan dengan durasi ini. Sisa pemain tersingkir karena kartu merah, tanpa mengetahui apakah ada kombinasi kemenangan dalam set kartu yang dikeluarkan.
Sekarang kami akan menghitung probabilitas pengumpulan kombinasi tiga kartu dengan barang yang sama. Ini adalah syarat untuk menerima hadiah.
Peluang Hadiah
Kami menguraikan permainan secara logis. Kami membuka kartu pertama, lalu pilih pasangan untuk kartu ini, pilih tiga untuk pasangan. Dengan pendekatan ini, kita dapat menghitung probabilitas mendapatkan 3 kartu yang identik dalam tiga upaya atau lebih, berdasarkan fakta bahwa ada 26 produk dalam permainan.
Untuk tugas dengan jumlah tes atau tes yang tetap, jika hasil dari setiap tes hanya dapat berhasil atau gagal, tes independen, dan probabilitas keberhasilan tetap konstan selama percobaan, kami akan menggunakan rumus Bernoulli - dalam Excel, fungsi BINOM.DIS.
Menggunakan fungsi BINOM.RASP, Anda dapat menghitung, misalnya, probabilitas bahwa dua dari tiga bayi baru lahir berikutnya adalah anak laki-laki. Berapa probabilitas menemukan tiga hal yang sama dalam tiga upaya?
= BINOM.RASP (3; 3; 1/26; 0) dengan mask
= BINOM.DISP (jumlah keberhasilan; jumlah percobaan; probabilitas keberhasilan; integral)
Atau di sini adalah rumus untuk menghitung probabilitas mendapatkan 3
barang identik dan tertentu dalam 8 upaya.
= BINOM.RASP (3; 8; 1/26; 0), bukan?
Tidak juga. Ketika kami mencapai durasi permainan dalam 4 percobaan, tidak memungkinkan pembukaan merah dan terus bermain, kami mendapatkan situasi dengan kemungkinan dua pasang untuk memilih tiga kemenangan.
Secara konvensional, dua barang dari 26 adalah A dan B. Kartu terbuka kami adalah A-B-A-B. Probabilitasnya tidak lagi 1/26, tetapi 1/26
+ (1/26) * "Probabilitas dua pasangan selama durasi permainan tertentu .
"Probabilitas dua pasangan selama durasi permainan = BINOM.DISP (2; 5; 1/26; 0) ^ 2
Saat mencapai game yang lebih lama dengan upaya ke-7, kami mendapatkan kombinasi seperti A-B-A-B-B-B. Ini berarti bahwa probabilitasnya sekarang sama
= 1/26 * (1 + BINOM.RASP (2; 7; 1/26; 0) ^ 2 + BINOM.RASP (2; 7; 1/26; 0) ^ 3) dan kami mencari kartu ketiga untuk 1, 2 atau tiga pasang.
UPD: Juga, pada awalnya kami tidak memperhitungkan bahwa upaya pertama dalam perhitungan kemenangan kami, dibersihkan dari kemungkinan memilih yang merah, adalah penemuan salah satu dari 26 produk, yang berarti 100% sukses. Jumlah pengulangan suatu produk dalam matriks adalah jumlah kecocokan dengan satu produk, yang berarti bahwa dua pengulangan untuk satu produk cukup untuk menang, dan tidak cocok dengan 3 dengan hasil prediksi yang spesifik. Dengan demikian, pilihan pertama dari kartu apa saja dan dua upaya untuk mengambil dua lebih dari bentuk yang sama total dari tiga percobaan.Mengetahui probabilitas, kami sedang membangun sebuah matriks:
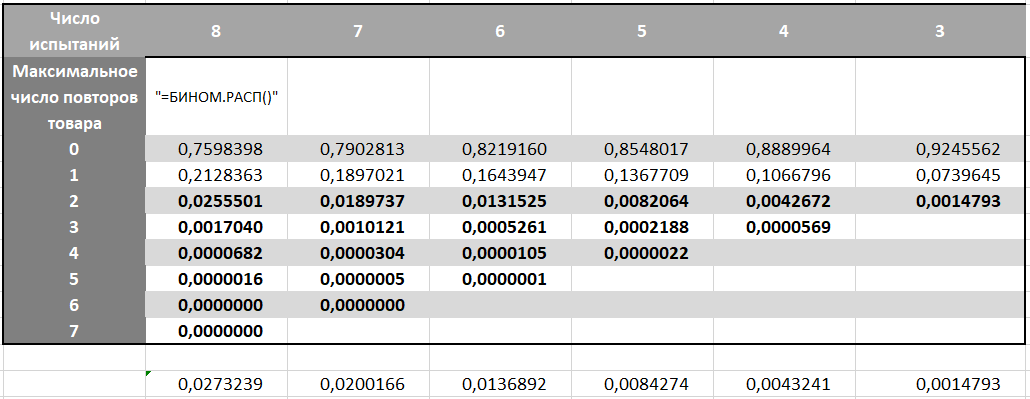
Di dalamnya kita menemukan probabilitas setiap jumlah maksimum pengulangan suatu produk untuk setiap varian durasi permainan. Ingat bahwa kemungkinan menang berubah pada percobaan ke-4 dan ke-7, yang berarti kita memperhitungkannya dalam rumus BINOM.RASP
Kami membutuhkan opsi dengan jumlah pengulangan maksimum untuk setiap produk 3 atau lebih. Karena permainan akan berhenti segera setelah kami mengumpulkan ketiganya, kami menambahkan probabilitas dengan kolom di area dalam huruf tebal.
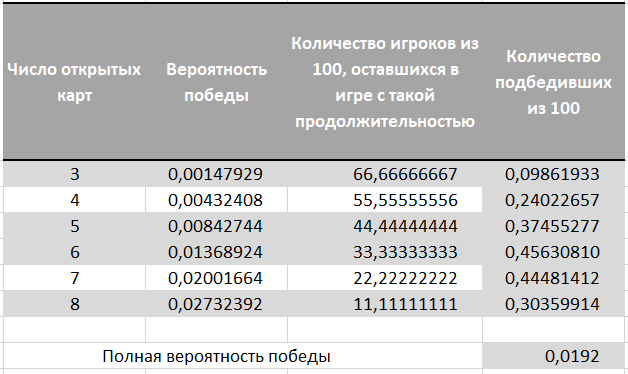
Selanjutnya, kami melipatgandakan peluang setiap durasi game dengan peluang memenangkan hadiah dengan durasi seperti itu. Kesimpulannya, kami mendapatkan probabilitas 0,0192 atau 192 pemenang per 10.000 pemain.
Ya, memang itu adalah probabilitas yang sangat rendah. Tidak semuanya 25%. Mari kita lihat kembali aturan mainnya:
8. Dana hadiah:
8.1. Hadiah yang tersedia: nama dan jumlah
...
Total 166.000
Kami membagi 116.000 dengan probabilitas menang dan mendapatkan sekitar 6 juta peserta untuk memainkan semua hadiah. Ingatlah bahwa pada 1 Januari 2018, menurut Rosstat, ada 146.938.921 penduduk tetap di Rusia. Rupanya, ini adalah ide dari penyelenggara permainan - untuk memberikan kesempatan untuk memenangkan hampir setiap warga negara Rusia.UPD: Probabilitas akhir telah berubah setelah perubahan. Sekarang kita dapat menguji perhitungan kita dalam praktek dengan bantuan skrip, tetapi karunia pikiran Tuhan dari para ahli matematika dan ahli teori dari generasi sebelumnya adalah luar biasa, yang menghitung sejumlah kemungkinan, menemukan solusi yang tepat di atas kertas dan menggunakan eksperimen mental.Analisis kode menunjukkan kepada penulis publikasi asli bahwa bahkan sebelum dimulainya permainan, skrip “mengetahui” hasilnya, tetapi tidak ada yang tahu hasil yang ditentukan sebelumnya yang akan diberikan skrip kepada pengguna tertentu. Mengetahui sisi matematis dari masalah ini, Anda akan dapat membuat kesimpulan sendiri tentang kejujuran penyelenggara.