Logika fuzzy untuk mengontrol
Teks ini didasarkan pada bahan-bahan dari buku V. Gostev. "Regulator fuzzy dalam sistem pemodelan otomatis." Seperti semua publikasi serius tentang topik ini, buku ini dipenuhi dengan perhitungan matematis dan sulit bagi pembaca yang tidak siap. Sementara itu, prinsip-prinsip membuat dan menggunakan logika fuzzy sendiri cukup sederhana dan jelas. Teks ini adalah upaya untuk menerjemahkan contoh dari buku dari bahasa matematika ke teknik.
Urutan yang mungkin untuk merancang pengontrol yang didasarkan pada logika fuzzy ditunjukkan dengan secara berurutan menyulitkan aturan logis dan memilih parameter menggunakan metode optimisasi.
Pernyataan masalah
Pertimbangkan sintesis pengontrol PID digital dan pengontrol fuzzy untuk sistem kendali rudal berdasarkan sudut serangan. Dengan menggunakan pemodelan matematika, kami menentukan proses dalam sistem dan memberikan penilaian komparatif kualitas sistem menggunakan pengontrol yang disintesis.
Mengambil sudut serang sebagai koordinat keluar rudal:  dan untuk input mengoordinasikan sudut kemudi
dan untuk input mengoordinasikan sudut kemudi  tentukan fungsi transfer roket dalam bentuk:
tentukan fungsi transfer roket dalam bentuk:
 dimana:
dimana:
 - koefisien konversi roket,
- koefisien konversi roket,
 - koefisien redaman,
- koefisien redaman,
 - konstanta waktu.
- konstanta waktu.
Selanjutnya, "fungsi transfer" digunakan tidak dalam definisi klasik yang ketat, sebagai rasio transformasi Laplace.
Dalam studi tentang sistem kontrol, anggaplah bahwa ketergantungan parameter roket pada waktu penerbangan ditentukan sebagai berikut:

Untuk menyederhanakan perhitungan, kami menjelaskan mekanisme kemudi dengan fungsi transfer dari tautan penyatuan  Dalam hal ini, input sistem
Dalam hal ini, input sistem  - diberikan angle of attack, output sistem
- diberikan angle of attack, output sistem  Apakah sudut serangan dikerjakan oleh roket, m (t) adalah sinyal kontrol pada output controller, dan objek kontrol dijelaskan oleh fungsi transfer umum:
Apakah sudut serangan dikerjakan oleh roket, m (t) adalah sinyal kontrol pada output controller, dan objek kontrol dijelaskan oleh fungsi transfer umum:

(Roda kemudi dan roket analog termasuk dalam objek kontrol).
Hukum variasi dari tindakan input diberikan oleh polinomial:

Penting untuk mengembangkan pengontrol yang memastikan pengembangan efek input menggunakan pengontrol PID dan pengontrol yang didasarkan pada logika fuzzy.
Untuk memilih koefisien regulator.
Bandingkan transien dengan pengontrol PID dan pengontrol berdasarkan logika fuzzy.
Model objek dinamis
Buat model dinamis dalam lingkungan pemodelan struktural.
Rangkaian model itu sendiri ditunjukkan pada Gambar 1.
Tindakan yang ditentukan diatur dalam bentuk blok konstan, variabel dari skrip ditetapkan sebagai parameter. Parameter fungsi transisi diatur dalam bentuk variabel.
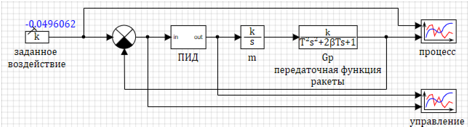 Gambar 1. Diagram model dinamis roket.
Gambar 1. Diagram model dinamis roket.Pengaturan regulator
Blok PID adalah submodel (Gbr. 2), yang menggunakan blok standar "Discrete PID controller". Tingkat pengambilan sampel dipilih sama dengan 0,001 detik.
 Gambar 2. Kontroler PID dengan sirkuit tuning.
Gambar 2. Kontroler PID dengan sirkuit tuning.Parameter pengontrol diatur dalam bentuk nama sinyal global dari proyek
Kp, Ki, Kd. Ini memungkinkan Anda untuk mengubah parameter selama simulasi, dan menyesuaikan regulator.
Blok
"Optimasi" digunakan untuk menyesuaikan regulator, kriteria optimasi adalah standar deviasi minimum.
Unit optimisasi melakukan optimisasi selama proses transisi. Hasil optimasi adalah vektor tiga koefisien, yang dikirim ke blok "Tulis ke daftar sinyal", di mana nilai yang dihitung ditransfer ke sinyal dan, karenanya, nilai-nilai koefisien PID berubah. Untuk mengkonfigurasi controller, kami menetapkan parameter optimasi berikut:
Nilai awal dari semua koefisien
1.Rentang untuk pilihan diatur dari
-50 hingga
+50Akurasi seleksi
0,001Deviasi standar maksimum setelah optimasi
0,01Dalam kasus ini, unit optimisasi menghitung nilai-nilai optimal koefisien berikut:
Kp = -1.7498597; Ki = 17.891995; Kd = 11.606602 .
Dengan koefisien ini, standar deviasi dalam transien yang diberikan adalah
0,008738090
Gambar 3. Transient.
| 
Gambar 4. Manajemen. |
Pengontrol logika fuzzy
Keuntungan utama dari pengontrol yang didasarkan pada logika fuzzy adalah kesederhanaan dan kejelasan pembentukan aturan untuk mengendalikan objek.
Misalnya, dalam buku "Regulator Fuzzy dalam Sistem Pemodelan Otomatis", aturan regulasi fuzzy untuk mengendalikan roket dengan sudut serangan dijelaskan dalam bentuk ekspresi matematika:

dimana

- kesalahan sistem, kesalahan perubahan kecepatan (turunan pertama), kesalahan akselerasi (turunan kedua);
m - mengontrol tindakan pada objek;

- estimasi linguistik kesalahan, laju perubahan kesalahan (turunan pertama) dari kesalahan dan turunan kesalahan kedua, dianggap sebagai himpunan fuzzy yang didefinisikan pada himpunan universal

;

- estimasi linguistik dari tindakan kontrol pada objek, dipilih dari set-set variabel
mPembaca mungkin bertanya: bagaimana, ibumu, aku minta maaf, mengerti?
Terkadang keraguan merayap dalam diri saya bahwa para ahli matematika sendiri mengerti apa yang mereka tulis. Di balik belokan matematis yang muskil, rahasia besar aturan regulasi fuzzy disembunyikan. Ini dia:
kurangi banyak
norma - jangan sentuh
kecil - peningkatanJika Anda menerjemahkan dari bahasa matematika burung ke dalam bahasa Rusia, maka ekspresinya

secara harfiah berarti sebagai berikut:
Jika
lebih dari normal dan
deviasi meningkat dan
laju pertumbuhan meningkat , maka kita
berkurang .
Jika
norma tidak berubah dan
kecepatan konstan , maka kita
tidak berubah .
Jika
kurang dari normal dan
jatuh dan
tingkat jatuh meningkat , maka
meningkat .
Jika Anda memahami apa yang sebenarnya tersembunyi di balik kabut matematika, maka Anda dapat mendekati pembuatan regulator secara lebih sadar dan mendapatkan hasil yang lebih menarik.
Sedikit teori
Untuk mengatasi masalah penyesuaian sudut serangan, kita harus mendapatkan tiga istilah dari nilai deviasi terus menerus - kurang, norma, lebih. Hal yang sama harus dilakukan untuk turunan pertama dari penyimpangan dan turunan kedua dari penyimpangan. Ini adalah tahap pertama inferensi fuzzy - pentahapan.
Untuk mendapatkan persyaratan, kita perlu mengatur nilai numerik dari parameter untuk setiap istilah. Sebagai contoh: "Little" = -1; "Norm" = 0; “Banyak” = 1. Untuk pentahapan, kami akan menggunakan fungsi segitiga. Fungsi tumbuh saat Anda mendekati nilai yang ditetapkan, dan berkurang saat Anda menjauh. Dua opsi untuk fungsi segitiga ditunjukkan pada Gambar 5:

 Gambar 5. Fungsi keanggotaan segitiga.
Gambar 5. Fungsi keanggotaan segitiga.Mengetahui penyimpangan (x1), kita dapat menemukan nilai-nilai fungsi keanggotaan untuk istilah lebih (garis merah), norma (garis hijau), kurang (garis biru). Nilai akan berkisar dari 0 hingga 1.
Harap dicatat bahwa pada bagan kiri fungsi ekstrem tidak cukup "segitiga". Jika kita mempertimbangkannya dari sudut pandang matematika abstrak, maka fungsi pada grafik yang tepat lebih "indah". Tetapi, jika Anda mengingat "rahasia utama aturan inferensi fuzzy", maka bagan kiri lebih benar. Sebenarnya:
Pertimbangkan aturan
"Tambah - kecil" , jika kita memiliki nilai -1, maka
"kecil" = 1 (garis merah) berlaku untuk kedua grafik. Dan jika kita memiliki nilai -2? Secara logis, kita juga harus
menambahkan . Pada grafik kiri di -2 itu adalah:
"little = 1" , tetapi pada grafik kanan kita memiliki
"sedikit" = 0, yang jelas tidak benar. Hal yang sama berlaku untuk aturan
"mengurangi banyak .
"Bertahap dengan fungsi segitiga "jujur" dapat mengarah pada fakta bahwa ketika nilainya melampaui kisaran definisi fungsi, kita mendapatkan 0 untuk semua istilah, yang, pada gilirannya, dapat menyebabkan tidak adanya dampak pada objek.
Masalah terbalik adalah dephasification. Untuk menghitung dampak, Anda perlu melakukan transformasi terbalik - kami memiliki nilai fungsi keanggotaan untuk mengurangi, tidak mengubah, meningkatkan rentang (
0 ... 1 ) (fungsi segitiga) dan rentang efek yang dapat kita miliki, dan kita harus mendapatkan salah satu dari tiga istilah angka adalah dampak khusus.
Anda bisa mendapatkan dampaknya dengan berbagai cara, misalnya, di tengah-tengah massa gambar. Gambar 6 menunjukkan keadaan pengontrol, di mana nilai-nilai dari istilah berkurang
0,3 tidak berubah
0,6 dan meningkat
0,8 dengan kisaran dampak regulasi
-30,30 dampak yang dihasilkan =
4,1.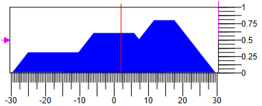 Gambar 6. Defazifikasi tindakan kontrol
Gambar 6. Defazifikasi tindakan kontrolPilihan lain untuk defazifikasi adalah di pusat massa poin. Gambar 7 menunjukkan opsi di mana, untuk nilai yang sama dari istilah dan rentang kontrol, kami mendapatkan jawaban lain
8.82 :
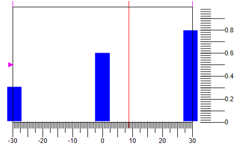 Gambar 7. Defazifikasi oleh pusat massa titik.
Gambar 7. Defazifikasi oleh pusat massa titik.Harus dipahami bahwa selain metode inferensi, bentuk fungsi keanggotaan juga mempengaruhi hasilnya. Misalnya, Anda dapat memilih fungsi segitiga seperti itu yang alasnya sama, hanya simpulnya yang berbeda. (lihat gbr. 8).
 Gambar 8. Fungsi keanggotaan segitiga dengan satu basis.
Gambar 8. Fungsi keanggotaan segitiga dengan satu basis.Dalam hal ini, untuk mengurangi hasil faseisasi dengan nilai yang sama dari istilah 0.3, jangan berubah 0,6 dan meningkat -0,8 dengan kisaran dampak regulasi -30, 30 dampak yang dihasilkan =
5,27 .
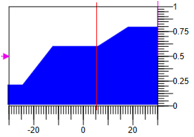 Gambar 9. Defazifikasi berdasarkan perhitungan area.
Gambar 9. Defazifikasi berdasarkan perhitungan area.Berbekal pengetahuan rahasia logika fuzzy, kami akan membuat model pengontrol. Kita membiarkan model roket sama seperti untuk pengontrol PID (lihat Gambar 1), tetapi dalam submodel pengontrol kita merakit rangkaian yang ditunjukkan pada Gambar 10.
 Gambar 10. Rangkaian pengontrol berdasarkan logika fuzzy.
Gambar 10. Rangkaian pengontrol berdasarkan logika fuzzy.Di pintu masuk ke regulator, ketidaksesuaian antara sudut serangan yang diberikan dan nyata (diukur) diterapkan. Setelah input, ada blok "Extrapolator", yang menyediakan konversi sinyal kontinu menjadi sinyal diskrit dengan periode pengambilan sampel tertentu (0,001 detik sama dengan pengontrol PID diskrit).
Setelah ini, penyimpangan turunan pertama dan kedua dihitung. Untuk melakukan ini, kami menghitung perbedaan antara nilai saat ini dan nilai dengan penundaan untuk periode kuantisasi, membaginya dengan waktu tunda (koefisien dalam blok perbandingan). Jadi, kita mendapatkan tiga input: kesalahan sistem, laju perubahan (turunan pertama) dari kesalahan, akselerasi (turunan kedua) dari kesalahan.
Nilai variabel input dikonversi oleh blok fase ke fungsi segitiga. Untuk setiap variabel, kami mendapatkan tiga variabel linguistik (total sembilan).
Demultiplexer membiakkan vektor menjadi variabel linguistik untuk membentuk aturan. Dalam diagram, nama-nama variabel ditandatangani dalam urutan pesanan mereka di vektor.
Deviasi dalam kasus kami adalah perbedaan antara set dan terukur, jika nilai negatif berarti sudut serangan lebih besar dari set, kita harus menguranginya. Dan karenanya, sebaliknya, jika deviasinya positif, maka sudut yang diukur lebih kecil dari sudut yang ditentukan, kita harus meningkatkannya.
(Lebih banyak - kurangi, kurangi - tambah, norma - jangan sentuh) .
Outputnya juga memiliki tiga variabel linguistik "mengurangi", "jangan berubah", "meningkat". Multiplexer mengumpulkan nilai-nilai ke dalam vektor dan mengirimkannya ke blok output fuzzy. Sekarang kita memiliki semua variabel, kita dapat menulis aturan inferensi fuzzy dalam bentuk diagram.
- Jika lebih dari normal dan deviasi meningkat dan laju pertumbuhan meningkat => menurun.
- Jika norma tidak berubah dan konstan => kita tidak berubah.
- Jika kurang dari normal dan jatuh dan laju jatuh meningkat => meningkat.
Semua variabel linguistik dalam aturan terhubung melalui blok logis “dan” dan terhubung ke output. Seperti dapat dilihat dari Gambar 10, rangkaian inferensi fuzzy logis secara praktis tidak berbeda dari sirkuit logis biasa, hanya blok logika fuzzy yang digunakan.
Mirip dengan menyetel pengontrol PID, kami menggunakan blok optimisasi.
Pertanyaannya tetap dengan parameter blok.
Sintesis pengontrol berbasis logika fuzzy
Tidak ada yang diberikan dalam hidup tanpa hasil, dan oleh karena itu, kesederhanaan aturan regulasi dikompensasi dengan jumlah parameter yang menggambarkan fungsi keanggotaan. Bahkan, jika Anda perlu memilih tiga koefisien untuk kontroler PID, maka dalam kasus logika fuzzy, hanya satu fungsi segitiga yang membutuhkan 3 angka untuk simpul. Jika untuk setiap variabel input kita membutuhkan 3 fungsi keanggotaan + 3 untuk output, ternyata kita perlu menetapkan 3 x 3 x 3 + 3 x 3 = 36 parameter!
Tapi tidak semuanya begitu sedih. Untuk perkiraan pertama dan pengaturan awal, semuanya dapat disederhanakan.
Setelah membuat beberapa asumsi untuk penyesuaian awal controller:
- Kami mengatur simetri fungsi sehubungan dengan nol, lalu alih-alih dua angka untuk maksimum dan minimum, Anda dapat menentukan satu - Max , dan, karenanya, akan didefinisikan sebagai rentang [ -Max ... Max ].
- Kami menetapkan distribusi fungsi yang seragam, maka kami dapat menghitung posisi semua simpul segitiga berdasarkan rentang yang diberikan.
- Untuk tiga fungsi, koordinat simpul didefinisikan sebagai –Max, 0, Max.
- Kami menetapkan bahwa dasar segitiga semua fungsi keanggotaan adalah sama.
Jadi, alih-alih 36 parameter independen, kita hanya perlu menentukan 4, deviasi maksimum dari 0 untuk tiga variabel input dan satu output, yaitu:
uMax - amplitudo dari tindakan kontrol
(-uMax ... uMax) ;
deltaMax - penyimpangan maksimum
(-deltaMax ... deltaMax) ;
divMax - turunan maksimum dari penyimpangan
(-divMax ... divMax) ;
div2Max - turunan kedua maksimum dari penyimpangan
(-div2Max ... div2Max)Dalam fungsi faseisasi dan inferensi fuzzy, kami menggunakan sinyal ini untuk menghitung parameter dengan mempertimbangkan asumsi yang diterima.
Pengaturan pengontrol diusulkan dalam buku oleh V.V. Gostev "Regulator fuzzy dalam sistem pemodelan otomatis", untuk kasus faseisasi oleh tiga fungsi keanggotaan, parameter berikut diusulkan:
uMax = 30 - amplitudo dari tindakan kontrol;
deltaMax = 0,01 - penyimpangan maksimum;
divMax = 0,07 - turunan maksimum dari penyimpangan;
div2Max = 1 adalah turunan maksimum kedua dari deviasi.
Perbandingan Sementara
Pada grafik transien, kebetulan dari efek yang diberikan dan hasil yang diperoleh hampir lengkap:

Gambar 11.a Transient. Kontroler PID
| 
Gambar 11.b Transient. Logika fuzzy
|
Perbedaan yang jelas dapat dilihat pada grafik dari deviasi dan tindakan kontrol yang diperoleh:

Gambar 12.a. Manajemen Kontroler PID
| 
Gambar 12.b. Manajemen Logika fuzzy |
Dari perbandingan angka-angka, terlihat bahwa kontroler fuzzy memberikan lebih sedikit kesalahan, dan transien yang lebih baik.
Mari kita bandingkan transien dalam sistem jika kita menetapkan tindakan kontrol bertahap. Hasil pada Gambar 13:

Gambar 13.a. Efek langkah. Kontroler PID.
| 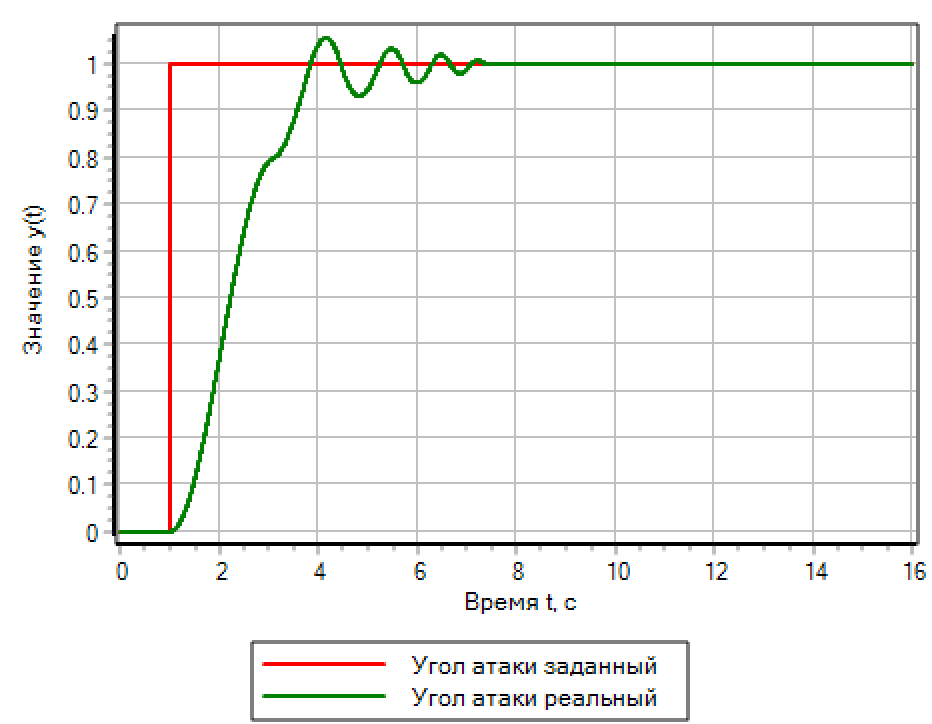
Gambar 13.b. Efek langkah. Logika fuzzy. |
Untuk tindakan bertahap, pengontrol berbasis logika fuzzy memberikan kualitas transien terbaik. Kontroler PID, yang secara otomatis diatur ke proses yang mulus, menyebabkan osilasi dengan overshoot yang dua kali langkah yang ditetapkan.
Penyesuaian kontroler berdasarkan fuzzy logic dengan metode optimisasi
Mari kita coba memilih parameter pengontrol fuzzy dengan metode optimisasi, sama seperti kita memilihnya untuk pengontrol PID. Sebagai kriteria, kami menetapkan standar deviasi kurang dari 0,001.
Perlu dicatat bahwa metode ini tidak sepenuhnya benar, karena bagi para profesional jelas sudut mana dan kecepatan mana yang maksimum dan minimum untuk setiap karya konser, yang memungkinkan Anda untuk menetapkan batasan pada parameter yang dioptimalkan secara lebih sadar, kami menetapkan parameter default dan melihat apa yang terjadi.
Metode optimasi dengan pengaturan default menghitung nilai berikut dari rentang parameter optimasi:
uMax = 19.377 - amplitudo dari tindakan kontrol;
deltaMax = 1.095 - penyimpangan maksimum;
divMax = 0,01 - turunan maksimum dari penyimpangan;
div2Max = 2.497 adalah turunan maksimum kedua dari deviasi.
Dalam kasus optimalisasi simpangan, parameter yang diperoleh memberikan akurasi yang ditentukan, namun ini menyebabkan osilasi frekuensi tinggi dari aksi kontrol.
Fungsi transisi dan tindakan kontrol disajikan pada Gambar 14.a
 Gambar 14.a. Logika fuzzy. Pengaturan penyimpangan. Gambar 14.a. Logika fuzzy. Pengaturan penyimpangan.
| 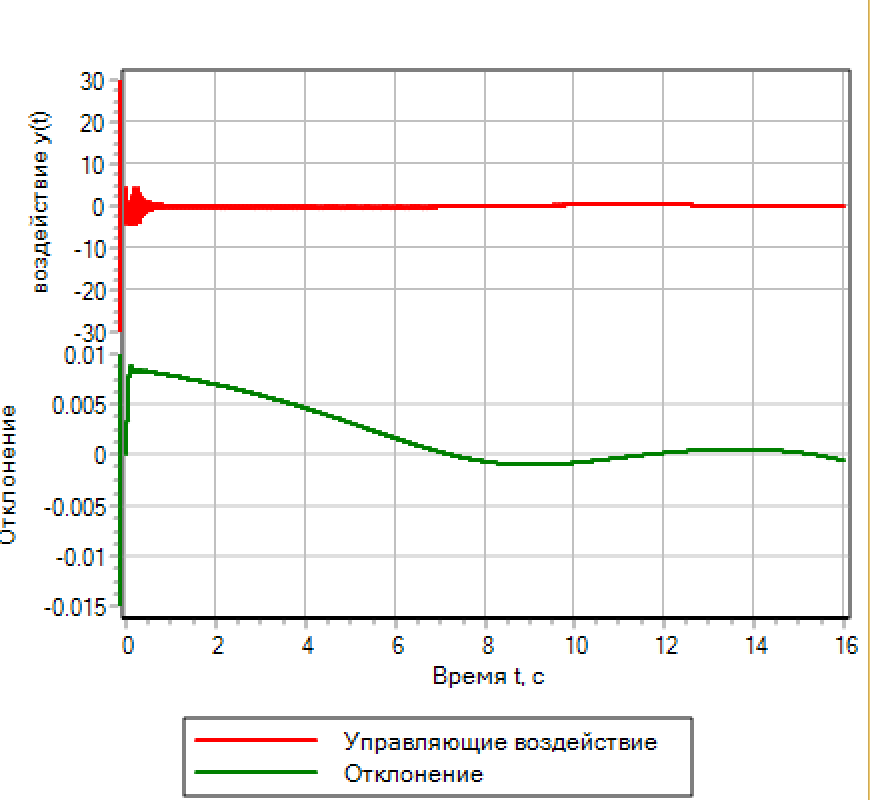 Gambar 14.b. Logika fuzzy. Pengaturan dengan penyimpangan dan jumlah respons. Gambar 14.b. Logika fuzzy. Pengaturan dengan penyimpangan dan jumlah respons. |
Untuk meningkatkan proses transien, seseorang dapat menambah kriteria optimisasi jumlah penggantian regulator dari negatif ke nilai positif dari efek pengaturan (skema pada Gambar 15).
 Gambar 15. Skema untuk optimasi berdasarkan 2 kriteria.
Gambar 15. Skema untuk optimasi berdasarkan 2 kriteria.Perhitungan dengan metode optimisasi menurut dua kriteria memberikan nilai parameter berikut:
uMax = 19.714 - amplitudo dari tindakan kontrol;
deltaMax = 1.0496 - penyimpangan maksimum;
divMax = 0,01 - turunan maksimum dari penyimpangan;
div2Max = 1.7931 adalah turunan maksimum kedua dari deviasi.
Dapat dilihat bahwa ketika jumlah perjalanan ditambahkan ke kriteria optimisasi, adalah mungkin untuk mengurangi frekuensi switching regulator (lihat Gambar 14.b). Dengan demikian, kita dapat mengatakan bahwa metode pengoptimalan berfungsi bahkan ketika kita tidak tahu apa-apa tentang fisika objek dan cukup memilih parameter numerik tanpa memikirkan arti fisiknya.
Membuat pengontrol Anda sendiri berdasarkan logika fuzzy
Di atas, kami menciptakan controller sesuai dengan skema yang sudah disiapkan dan cukup sederhana, semua istilah variabel linguistik dihubungkan oleh operator logika I. Karena kami memiliki jumlah istilah yang sama pada input dan output, ini adalah solusi paling sederhana dan paling jelas.
Mari kita coba membuat pengontrol yang outputnya tidak memiliki 3 istilah, tetapi, misalnya, 5:
kurangi dengan cepat, kurangi, jangan ubah, tambah, tambah cepat . Dan di pintu masuk sama.
Mari kita ubah logika regulator, sebagai permulaan, sederhanakan algoritma kontrol sebanyak mungkin.Kami menuliskan aturan:1) Jika lebih besar dan tumbuh t => turun dengan cepat.2) Jika lebih => berkurang.3) Jika norma => tidak berubah.4) Jika kurang => tambah.5) Jika kurang dan memiliki menshaetsya => peningkatan pesat.Dalam hal ini, kami memiliki 5 istilah (5 fungsi segitiga) untuk variabel output. Kami menerima bahwa keduanya didistribusikan secara merata antara -uMax dan + uMax.Kami berasumsi bahwa fungsi segitiga disusun sedemikian rupa sehingga ketika fungsi keanggotaan istilah mengambil nilai maksimum, fungsi tetangga mengambil nilai nol (lihat Gambar 5).Sebagai parameter untuk output, hanya deviasi dan laju perubahan deviasi yang akan digunakan.Untuk mempercepat perhitungan, kami menggunakan pentahapan output dari metode dengan pusat gravitasi titik (lihat Gambar 7).Rangkaian pengontrol dalam hal ini akan terlihat seperti yang ditunjukkan pada Gambar 15.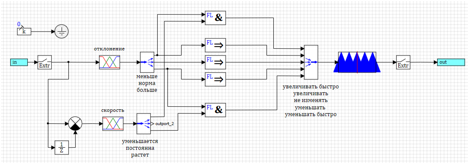 Gambar 15. Pengontrol yang disederhanakan berdasarkan logika fuzzy.Alih-alih rentang turunan kedua dari pengoptimal, nilai untuk istilah "kenaikan" akan diambil. Upaya untuk menyesuaikan regulator seperti itu dengan metode optimasi menunjukkan bahwa regulator disetel, tetapi kualitas regulasi kontrol sistem menyisakan banyak yang diinginkan.Hasil terbaik ditunjukkan pada Gambar 16.
Gambar 15. Pengontrol yang disederhanakan berdasarkan logika fuzzy.Alih-alih rentang turunan kedua dari pengoptimal, nilai untuk istilah "kenaikan" akan diambil. Upaya untuk menyesuaikan regulator seperti itu dengan metode optimasi menunjukkan bahwa regulator disetel, tetapi kualitas regulasi kontrol sistem menyisakan banyak yang diinginkan.Hasil terbaik ditunjukkan pada Gambar 16.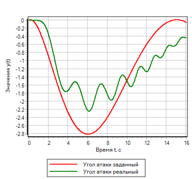 Gambar 16. Transien untuk pengontrol yang disederhanakan.Dapat dilihat bahwa regulasi sedang terjadi, tetapi tidak sama sekali seperti yang kita inginkan. Faktanya adalah bahwa kita menjalankan efek ketika penyimpangan telah terjadi. Mari kita coba nyalakan regulasi pada saat kita memiliki penyimpangan dalam norma, tetapi kecepatan menunjukkan bahwa itu akan bertambah atau berkurang.1) Jika kurang dan menurun => meningkat dengan cepat.2) Jika norma dan kenaikan => berkurang.3) Jika norma => tidak berubah.4) Jika norma dan menurun => meningkat.5) Jika lebih besar dan tumbuh => berkurang dengan cepat.
Gambar 16. Transien untuk pengontrol yang disederhanakan.Dapat dilihat bahwa regulasi sedang terjadi, tetapi tidak sama sekali seperti yang kita inginkan. Faktanya adalah bahwa kita menjalankan efek ketika penyimpangan telah terjadi. Mari kita coba nyalakan regulasi pada saat kita memiliki penyimpangan dalam norma, tetapi kecepatan menunjukkan bahwa itu akan bertambah atau berkurang.1) Jika kurang dan menurun => meningkat dengan cepat.2) Jika norma dan kenaikan => berkurang.3) Jika norma => tidak berubah.4) Jika norma dan menurun => meningkat.5) Jika lebih besar dan tumbuh => berkurang dengan cepat.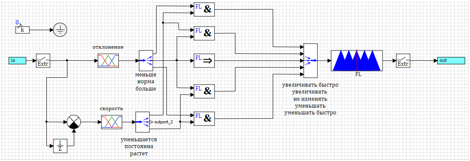 Gambar 17. Kontrol dengan tingkat perubahan penyimpangan.Hasil operasi pengontrol yang diatur oleh metode optimisasi disajikan pada Gambar 18a dan 18b.
Gambar 17. Kontrol dengan tingkat perubahan penyimpangan.Hasil operasi pengontrol yang diatur oleh metode optimisasi disajikan pada Gambar 18a dan 18b.
Gambar 18.a. Proses transisi.
| 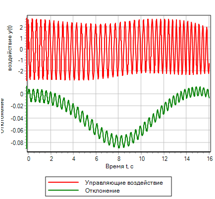
Gambar 18.b. Manajemen |
Kontrol atas tingkat perubahan penyimpangan secara signifikan meningkatkan transien. Namun, jika Anda hati-hati melihat seperangkat aturan logis, kami melihat bahwa penyimpangan tidak terlibat dalam manajemen. Jika efek langkah diberikan, pengontrol kontrol tidak akan menghasilkan tindakan kontrol. Gambar 19 menunjukkan contoh proses transien dengan aksi kontrol bertahap, dapat dilihat bahwa controller tidak memberikan aksi kontrol, walaupun deviasinya 1.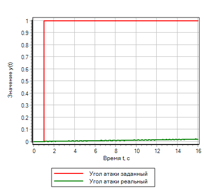
Gambar 19.a. Proses transisi. Langkah
| 
Gambar 19.b. Manajemen Langkah |
Untuk mengatasi penyimpangan cepat, kami menambahkan aksi kontrol untuk penyimpangan. Kami akan meningkat jika lebih sedikit dan mengurangi jika lebih banyak. Karena sudah ada aturan dalam aturan yang ditetapkan di mana kita mengurangi dan meningkatkan, kita menggunakan operator logis atau:1) Jika kurang dan menurun => meningkat dengan cepat.2) Jika ( norma dan meningkat ) atau lebih => berkurang.3) Jika norma => tidak berubah.4) Jika ( norma dan menurun ) atau kurang => meningkat.5) Jikalebih besar dan berkembang => berkurang dengan cepat.Rangkaian pengontrol sesuai dengan aturan ini disajikan pada Gambar 20.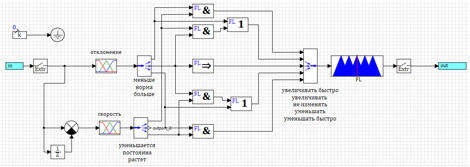 Gambar 20. Pengontrol dengan kontrol oleh deviasi dan laju perubahan.Sebagai hasil dari modifikasi, kualitas proses transisi dengan tindakan yang mulus praktis tidak berubah, namun, dengan tindakan bertahap, regulator mulai mengerjakan langkah dan membawa sudut serangan roket ke yang ditentukan (lihat Gambar 21).
Gambar 20. Pengontrol dengan kontrol oleh deviasi dan laju perubahan.Sebagai hasil dari modifikasi, kualitas proses transisi dengan tindakan yang mulus praktis tidak berubah, namun, dengan tindakan bertahap, regulator mulai mengerjakan langkah dan membawa sudut serangan roket ke yang ditentukan (lihat Gambar 21).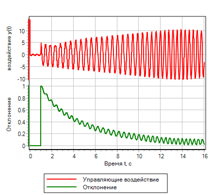
Gambar 21.a. Proses transisi. Langkah
| 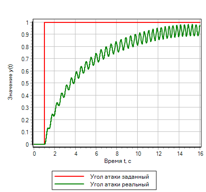
Gambar 21.b. Manajemen Langkah |
Sebagai kesimpulan, mari kita sekali lagi "meningkatkan" regulator kami.Mari kita coba gunakan turunan kedua dari deviasi, untuk memulai dampak, sebelum deviasi dan kecepatannya berubah. Bahkan, dengan penerapan kekuatan, kita memiliki akselerasi yang sudah bisa kita tanggapi.Mari kita coba tambahkan turunan kedua ke dalam hukum regulasi alih-alih turunan pertama kecepatan. Kami akan memiliki efek pengaturan tambahan dalam kasus ketika turunan kedua kami menunjukkan bahwa akan ada penyimpangan. Aturan umum akan terlihat hampir sama, hanya dalam tanda kurung kami memiliki tiga istilah, penyimpangan dan kecepatan normal, dan turunan kedua menyimpang:1) Jika kurang dan menurun => meningkat dengan cepat.2) Jika (normal dan konstan dan berakselerasi ) atau lebih => berkurang .3) Jika norma => tidak berubah.4) Jika ( normal dan konstan dan melambat ) atau kurang => meningkat.5) Jika lebih besar dan tumbuh => berkurang dengan cepat .Rangkaian regulator ini ditunjukkan pada Gambar 22. Untuk menghemat ruang pada sirkuit, ekspresi logis “dan” yang tertulis dalam aturan dalam tanda kurung dihitung dalam submodel bertanda “ & ”.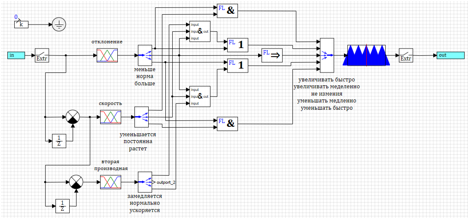 Gambar 22. Kontroler logika fuzzy dengan kontrol turunan kedua.Setelah memilih parameter dengan metode optimasi untuk penyimpangan dan jumlah inklusi, parameter berikut diperoleh:uMax = 27.4983 - amplitudo dari tindakan kontrol;deltaMax = 0,0433 - penyimpangan maksimum;divMax = 0,0966 - turunan maksimum dari penyimpangan;div2Max = 1.0828 - turunan kedua maksimum dari penyimpangan.Proses sementara ditunjukkan pada Gambar 23. Dapat dilihat bahwa regulator yang dihasilkan memiliki kinerja terbaik dari semua yang dipertimbangkan di atas, tetapi untuk efek yang diberikan. Penyimpangan dan tindakan kontrol adalah minimum dari semua yang dipertimbangkan dalam teks ini.
Gambar 22. Kontroler logika fuzzy dengan kontrol turunan kedua.Setelah memilih parameter dengan metode optimasi untuk penyimpangan dan jumlah inklusi, parameter berikut diperoleh:uMax = 27.4983 - amplitudo dari tindakan kontrol;deltaMax = 0,0433 - penyimpangan maksimum;divMax = 0,0966 - turunan maksimum dari penyimpangan;div2Max = 1.0828 - turunan kedua maksimum dari penyimpangan.Proses sementara ditunjukkan pada Gambar 23. Dapat dilihat bahwa regulator yang dihasilkan memiliki kinerja terbaik dari semua yang dipertimbangkan di atas, tetapi untuk efek yang diberikan. Penyimpangan dan tindakan kontrol adalah minimum dari semua yang dipertimbangkan dalam teks ini.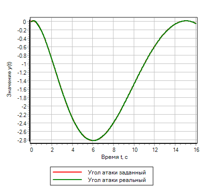
Gambar 23.a. Proses transisi.
| 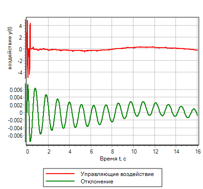
Gambar 23.b. Manajemen |
Kesimpulan
Kontroler berbasis logika fuzzy dapat memberikan kualitas transien yang lebih tinggi untuk kontrol roket daripada kontroler PID.Menyesuaikan pengontrol berdasarkan logika fuzzy dapat dilakukan menggunakan alat optimisasi.Kontroler yang didasarkan pada logika fuzzy memberikan fleksibilitas yang lebih besar dalam penyetelan dan kualitas transien yang lebih baik. Tetapi membutuhkan pengaturan lebih banyak parameter.Unduh arsip model yang digunakan dalam persiapan teks ini, untuk studi independen di sini ...