Geekly articles weekly

Penentuan karakteristik balistik-temporal dari gerakan pusat massa penerjun payung dari pesawat terbang

Pendahuluan


Untuk menentukan karakteristik balistik-temporal dari gerakan pusat massa penerjun payung, kita harus memilih model matematika sederhana yang cukup mudah diakses untuk penelitian analitik dan pada saat yang sama mempertahankan fitur paling khas dari objek asli.

Untuk membangun model matematika sederhana dari pergerakan penerjun payung, dilakukan analisis, penentuan, sistematisasi parameter konstan dan waktu.

Metode reguler dan cukup dibenarkan untuk membangun model matematika nonlinear saat ini tidak ada, namun, untuk memecahkan masalah tertentu, dengan komposisi yang tepat dari sistem awal persamaan diferensial nonlinear, metode numerik untuk menyelesaikannya dapat memberikan hasil yang cukup memadai.

Tujuan dari publikasi ini adalah untuk menyusun dan menyelesaikan secara numerik sistem persamaan diferensial yang menggambarkan semua tahapan pergerakan pendaratan penerjun payung dari pesawat terbang, dengan mempertimbangkan efek perubahan ketinggian dan suhu kepadatan massa udara.

Karakteristik balistik-temporal dari gerakan penerjun payung


Parameter variabel konstan dan terbatas meliputi:

H - ketinggian pelepasan penerjun payung;
V0 - kecepatan pesawat;
k - berat, tinggi penerjun payung;
g adalah percepatan gravitasi;
ρ adalah kepadatan udara;
T adalah suhu udara.

Parameter sementara (variabel) meliputi:

tn - waktu pendaratan,
w adalah kecepatan angin;
V adalah kecepatan penerjun payung;
u adalah kecepatan arus naik (turun);
d - drift (jarak dari proyeksi ke dasar titik ejeksi ke titik touchdown);
C adalah koefisien hambatan objek pendaratan;
Bagian tengah dari objek pendaratan.

Tahap lompat


Tahap pertama adalah jatuh bebas setelah pemisahan dari pesawat:



Tahap kedua adalah penurunan parasut stabil:



Properti utama paraset penstabil adalah stabilisasi parasut di posisi yang paling nyaman bagi parasut utama.

Tahap ketiga - mengisi kubah parasut utama:



Tahap keempat adalah penurunan parasut terbuka:



Kompilasi sistem persamaan diferensial untuk semua tahap lompatan parasut


Kami memilih sistem koordinat tetap OXY yang berpusat di titik ejeksi O. Sumbu OX bertepatan dengan arah komponen horizontal kecepatan pesawat. Sumbu OY diarahkan vertikal ke atas dalam arah yang berlawanan dengan kecepatan vertikal penerjun payung.

Kami akan menganggap bahwa pergerakan penerjun payung itu datar, dan terjadi di pesawat OXY. Model lompatan ini dapat dianggap sebagai model lompatan dalam cuaca tenang tanpa memperhitungkan pengaruh angin.

Kami percaya bahwa, selain berat, penerjun payung dipengaruhi oleh kekuatan hambatan udara sebanding dengan kuadrat kecepatan penerjun payung:

,
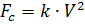
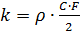
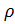
dimana: , - kerapatan udara, koefisien seret C, bagian tengah tubuh.

Dengan meningkatnya ketinggian, suhu udara berubah:



Temperatur minimum sudah tercapai pada ketinggian 10 km. dan -55 ° C Kepadatan udara juga tergantung pada tekanan. Oleh karena itu, ketika menghitung balistik lompatan parasut, akan lebih mudah untuk menggunakan rumus berikut untuk menentukan kepadatan udara [1]:

,
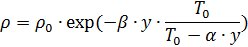
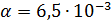
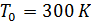
dimana K / m; - suhu di permukaan laut; y adalah ketinggian dalam m; - kepadatan udara pada y = 0; .

Daftar
# -*- coding: utf8 -*- from numpy import* import matplotlib.pyplot as plt beta=1.25*10**-4 alfa=6.5*10**-3 T0=300 y=arange(0,10000,1) x=[exp(-beta*w*T0/(T0-alfa*w)) for w in y] plt.title("  \n    ") plt.plot(x,y) plt.ylabel('  .') plt.xlabel(' ') plt.grid(True) plt.show()




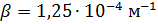
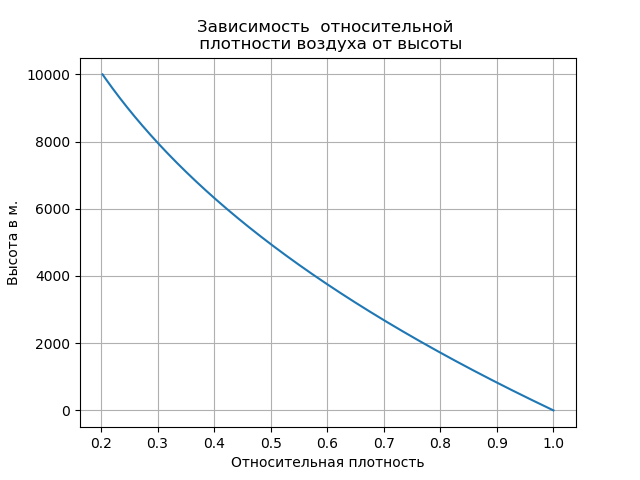
Dalam praktik perhitungan, kuadrat pertumbuhan diambil sebagai bagian tengah tubuh; nilai C ditemukan dari tabel [2]:



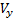
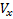
Θ menunjukkan sudut kemiringan lintasan. Di bawah asumsi yang dibuat untuk komponen , vektor kecepatan V yang kita miliki:



Membagi dengan m sisi kiri dan kanan persamaan dari sistem yang dihasilkan dan menunjukkan melalui r, kita mendapatkan:

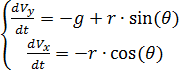
(1)

Kami menuliskan persamaan gerak skydiver dalam bentuk sistem persamaan diferensial untuk fungsi V, θ, y (t), x (t).

Mengingat bahwa:

,
,
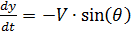
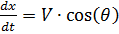
dan membedakan rasio waktu: , dengan mempertimbangkan sistem persamaan (1) yang kita dapatkan:

,
.

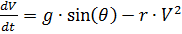
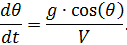
Jadi, di bawah kondisi awal:

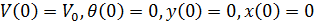
kami memiliki sistem persamaan diferensial berikut:



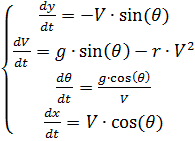
Solusi numerik dari sistem persamaan diferensial (2) menggunakan Python


Untuk menyelesaikan (2), kami menulis ulang dalam bentuk berikut, memperkenalkan gaya seret penstabil yang dikendalikan oleh waktu dan kepadatan udara



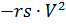
dan utama



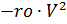
parasut, masing-masing, dikalikan dengan fungsi kontrol waktu ks (t) dan ko (t):



,

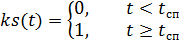
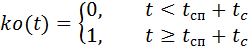
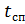
dimana: –– waktu jatuh bebas penerjun payung; - waktu operasi parasisasi stabilisasi sampai pembukaan yang utama.

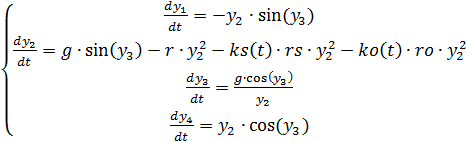
(3)

Daftar lengkap program disesuaikan untuk perubahan kepadatan udara
 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#   /2 rou0=1.29#  /3 Cp=0.3#    Cpar=0.75#     mp=120#    100+20=120 . s=0.8#   2 ss=1.5#   2 Cpars=0.35#     S=70#   2 tsp=40#    c. tssp=3 #      c. tpr=210#     . h=4000.0#    . V0=100.0#    / beta=1.25*10**-4 alfa=6.5*10**-3 T0=300 def ks(t): if t<= tsp: z=0 else: z=1 return z def ko(t): if t<= tsp+tssp: z=0 else: z=1 return z def f(y,t): y1,y2,y3,y4=y rou=rou0*exp(-beta*y1*T0/(T0-alfa*y1)) rp=0.5*Cp*rou*s/mp rpars=0.5*Cpars*rou*ss/mp rpar=0.5*Cpar*rou*S/mp return [-y2*sin(y3),g*sin(y3)-rp*(y2**2)-ko(t)*rpar*(y2**2)-ks(t)*rpars*(y2**2),g*cos(y3)/y2,y2*cos(y3)] t=arange(0,tpr,1) y0=[h,100,0,0] [y1,y2,y3,y4]=odeint(f, y0,t, full_output=False).T plt.figure() plt.title('     : %s .. \n   : %s /. \n   : %s /'%(h,V0,round(y2[tpr-tsp-tssp],0))) plt.plot(y1,y2*sin(y3),label='  .: %s c. \n     : %s . \n     : %s . '%(tsp,tssp,tpr-tsp-tssp)) plt.xlabel('  .') plt.ylabel('   /') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("-         \n   ") plt.plot(y1,y4) plt.xlabel('  .') plt.ylabel('     .') plt.grid(True) plt.figure() plt.title("     ") plt.plot(t,y2*sin(y3)) plt.xlabel('  .') plt.ylabel('   /.') plt.grid(True) plt.show()


Kami mendapatkan:







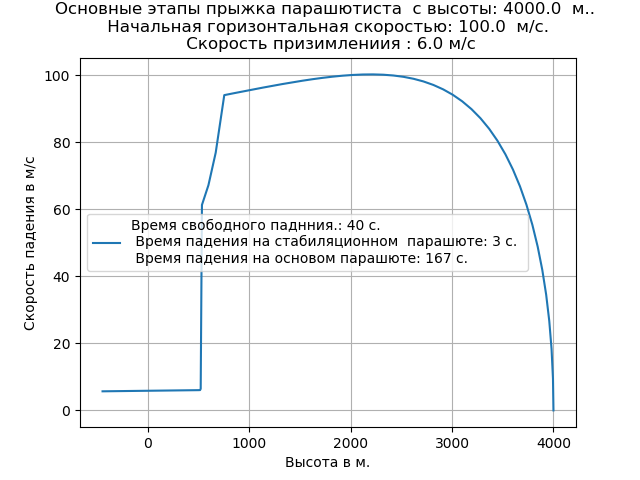
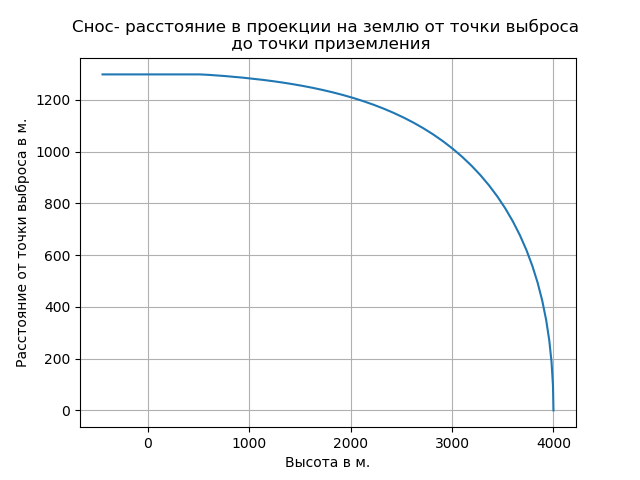
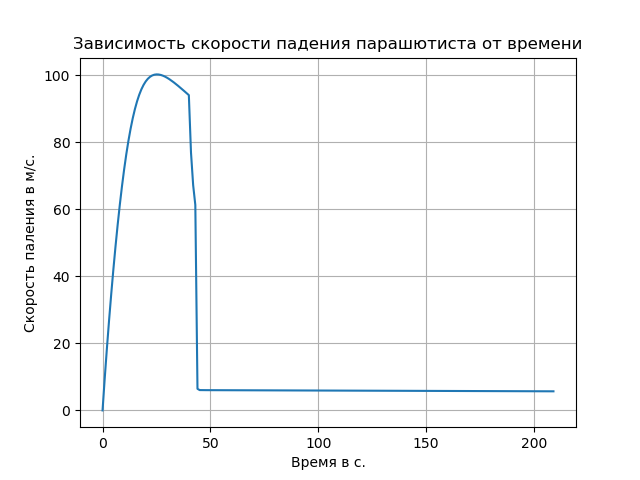
Memperhatikan udara yang dijernihkan menyebabkan peningkatan tingkat jatuh bebas dan mengubah sifat lintasan di bagian ini.

Masalah ini dapat diselesaikan dengan bantuan sistem dua persamaan diferensial, yang diberikan di bawah ini (tidak termasuk parasut dan perubahan kepadatan udara):



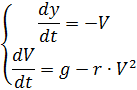
Perubahan kekuatan resistansi dan kerapatan udara ditunjukkan dalam daftar di bawah spoiler, dengan mempertimbangkan hal di atas dan tanpa penjelasan
# - * - coding: utf8 - * -
dari impor numpy *
dari scipy.integrate odeint impor
impor matplotlib.pyplot sebagai plt
m = 100
r0 = 1.3
c1 = 0,3
c2 = 0,6
c3 = 0,5
c4 = 0,75
S = 70
s = 0,8
ss = 1.5
g = 9,8
tsp = 6
tsbp = 10
tp = 90.0
h = 1000.0
beta = 1.25 * 10 ** - 4
alfa = 6.5 * 10 ** - 3
T0 = ​​300
def ks (t):
jika t <tsp:
z = 0
lain:
z = 1
kembali z
def ko (t):
jika t <tsp + tsbp:
z = 0
lain:
z = 1
kembali z
# dy1 / dt = y2
# dy2 / dt = g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S
return [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = arange (0.0, tp)
y0 = [h, 0,0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.title ("Skydiving dari 1000 dan 800 meter")
plt.plot (y1, y2, label = 'Ketinggian 1000 m')
h = 800.0
tsp = 6
tsbp = 2
tp = 80.0
def ks (t):
jika t <tsp:
z = 0
lain:
z = 1
kembali z
def ko (t):
jika t <tsp + tsbp:
z = 0
lain:
z = 1
kembali z
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S
return [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = arange (0.0, tp)
y0 = [h, 0,0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.plot (y1, y2, label = 'Tinggi 800 m')
plt.xlabel ('Tinggi dalam m.')
plt.ylabel ('Kecepatan pembakaran dalam m / s.')
plt.legend (loc = 'terbaik')
plt.grid (Benar)
plt.show ()

Kami mendapatkan:



Kesimpulan


Karakteristik balistik-temporal dari gerakan pusat massa penerjun payung dari pesawat udara ditentukan.

Referensi


  1. Tekanan atmosfer.
  2. Gerasimenko I.A. Pelatihan melalui udara: buku teks. M .: Penerbitan Militer, 1986. Bagian 1, P. 32.

Source: https://habr.com/ru/post/id413807/

More articles:


All Articles