Hai, Habr. Hari ini saya ingin mengembangkan topik
optimasi variasional dan memberi tahu bagaimana menerapkannya pada tugas memotong saluran yang tidak informatif dalam jaringan saraf (pemangkasan). Dengan menggunakannya, orang dapat secara relatif mudah meningkatkan "laju api" dari jaringan saraf tanpa menyekop arsitekturnya.
Gagasan mengurangi elemen yang berlebihan dalam algoritma pembelajaran mesin sama sekali tidak baru. Faktanya, ini lebih tua dari konsep pembelajaran mendalam: hanya saja sebelumnya cabang-cabang pohon yang menentukan ditebang, dan sekarang berbobot dalam jaringan saraf.
Gagasan dasarnya sederhana: kami menemukan dalam jaringan bagian dari bobot yang tidak berguna dan nolkan. Tanpa pencarian lengkap, sulit untuk mengatakan bobot mana yang benar-benar berpartisipasi dalam prediksi, dan yang hanya berpura-pura, tetapi ini tidak diperlukan. Berbagai metode regularisasi, Kerusakan Otak Optimal, dan algoritma lainnya bekerja dengan baik. Mengapa menghilangkan beban sama sekali? Ternyata hal ini meningkatkan kemampuan generalisasi jaringan: sebagai aturan, bobot yang tidak signifikan cukup dengan memasukkan noise ke dalam prediksi, atau secara khusus dipertajam untuk tanda-tanda dataset pelatihan (mis., Artefak pelatihan ulang). Dalam hal ini, pengurangan koneksi dapat dibandingkan dengan metode pemutusan neuron acak (putus) selama pelatihan jaringan. Selain itu, jika jaringan memiliki banyak nol, maka akan memakan lebih sedikit ruang dalam arsip dan dapat membaca lebih cepat pada beberapa arsitektur.
Kedengarannya bagus, tetapi jauh lebih menarik untuk membuang bukan bobot terpisah, tetapi neuron dari lapisan atau saluran yang terhubung sepenuhnya dari seluruh bundel. Dalam hal ini, efek kompresi jaringan dan akselerasi prediksi diamati jauh lebih jelas. Tapi ini lebih rumit daripada menghancurkan bobot individu: jika Anda mencoba melakukan Kerusakan Otak Optimal, mengambil seluruh bundel alih-alih satu koneksi, hasilnya kemungkinan tidak terlalu mengesankan. Untuk dapat menghilangkan neuron tanpa rasa sakit, perlu untuk membuatnya sehingga tidak memiliki koneksi yang berguna. Untuk melakukan ini, Anda perlu entah bagaimana mendorong neuron "kuat" untuk menjadi lebih kuat, dan yang "lemah" menjadi lebih lemah. Tugas ini sudah tidak asing lagi bagi kami: pada kenyataannya, kami memaksa jaringan untuk menjadi sparsity dengan beberapa pembatasan pengelompokan bobot.
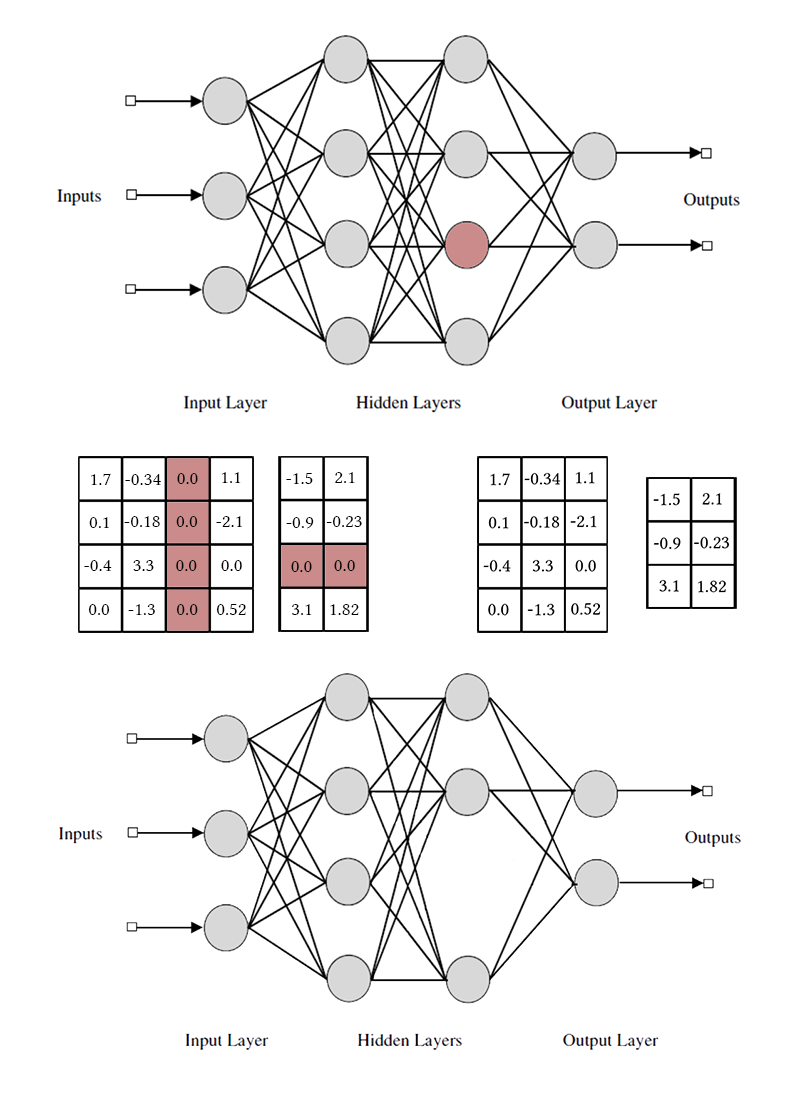
Perhatikan bahwa untuk menghapus satu saluran neuron atau konvolusional, Anda perlu memodifikasi dua matriks bobot. Saya tidak akan membedakan antara saluran convolutional dan neuron: pekerjaan dengan mereka adalah sama, hanya bobot yang dihilangkan secara spesifik dan metode transposisi yang berbeda.
Cara mudah: regularisasi grup L1
Untuk memulai, saya akan memberi tahu Anda tentang cara paling sederhana dan efektif untuk menghilangkan neuron ekstra dari jaringan - kelompok regularisasi LASSO. Paling sering digunakan untuk menjaga bobot yang tidak berguna dalam jaringan mendekati nol; itu sepele menggeneralisasi ke kasus saluran per kasus. Tidak seperti regularisasi reguler, kami tidak mengatur secara langsung berat atau aktivasi lapisan, idenya sedikit lebih rumit. [Pemangkasan Saluran untuk Mempercepat Jaringan Saraf Sangat Dalam; Yihui He et al; 2017]
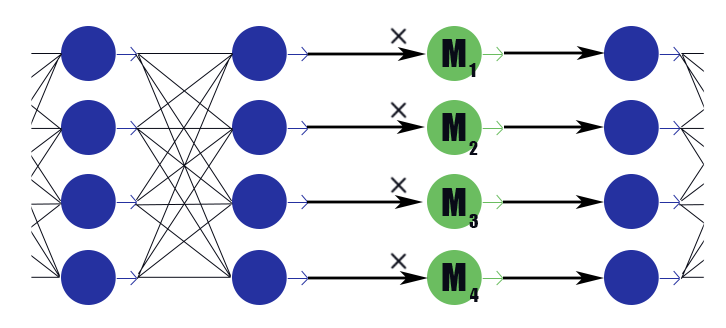
Pertimbangkan layer mask khusus dengan vektor bobot
M=( beta1, beta2, dots, betan) . Kesimpulannya hanyalah pekerjaan sesekali
M untuk kesimpulan dari lapisan sebelumnya, ia tidak memiliki fungsi aktivasi. Kami menempatkan di lapisan masking setelah setiap lapisan, saluran di mana kami ingin membuang, dan menimbang bobot dalam lapisan ini dengan regularisasi L1. Demikian berat topengnya
betai dikalikan dengan keluaran lapisan yang secara implisit memberlakukan batasan pada semua bobot yang menjadi dasar kesimpulan ini. Jika di antara bobot ini, ucapkan setengah berguna, lalu
betai akan tetap lebih dekat dengan persatuan, dan kesimpulan ini akan dapat mengirimkan informasi dengan baik. Tetapi jika hanya satu atau tidak sama sekali,
betai itu akan turun ke nol, yang akan mengatur ulang output dari neuron dan, pada kenyataannya, akan mengatur ulang semua bobot yang menjadi dasar kesimpulan ini (dalam hal fungsi aktivasi sama dengan nol di nol). Harap dicatat bahwa dengan cara ini jaringan menerima penguatan yang kurang negatif jika beratnya besar secara hukum, atau respons yang kuat secara hukum. Kegunaan neuron secara keseluruhan penting.
Ternyata rumus ini:
Dimana
lambda - pembobotan konstan loss'a network dan loss'a sparseness. Sepertinya rumus regularisasi L1 biasa, hanya istilah kedua berisi vektor lapisan penutup, dan bukan berat jaringan.
Setelah pelatihan jaringan, kita membahas neuron dan nilai maskingnya. Jika
betai lebih dari ambang tertentu, maka bobot neuron dikalikan dengan
betai jika kurang, maka unsur-unsur yang berhubungan dengan neuron dikeluarkan dari matriks bobot masuk dan keluar (seperti pada gambar sedikit lebih tinggi). Setelah ini, topeng bisa dijatuhkan dan jaringan selesai.
Dalam penerapan grup LASSO ada beberapa kehalusan:
- Regularisasi normal. Bersama dengan regularisasi bobot mask, regularisasi L1 / L2 harus diterapkan ke semua bobot jaringan lainnya. Tanpa ini, penurunan berat masking dalam kasus fungsi aktivasi tidak jenuh (ReLu, ELu) akan dengan mudah dikompensasi oleh peningkatan bobot, dan efek nulling tidak akan berfungsi. Ya, dan untuk sigmoid biasa, ini memungkinkan Anda memulai proses dengan lebih baik dengan umpan balik positif: Mi output tidak informatif menjadi lebih kecil, itulah sebabnya optimizer harus berpikir lebih kuat tentang setiap bobot spesifik, yang membuat output lebih tidak informatif, itulah sebabnya Mi berkurang lebih banyak dan sebagainya.
- Para penulis artikel juga menyarankan untuk memaksakan pembatasan bola pada berat lapisan |Wi|2=1 . Ini mungkin seharusnya berkontribusi pada "aliran" keseimbangan dari neuron yang lemah ke yang kuat, tetapi saya tidak melihat banyak perbedaan.
- Pelatihan push-pull. Para penulis artikel menyarankan secara bergantian melatih bobot normal dari jaringan saraf dan bobot masking. Ini lebih lama daripada mengajarkan segalanya pada satu waktu, tetapi seolah hasilnya sedikit lebih baik?
- Jangan lupa tentang fine tuning panjang jaringan (fine-tuning) setelah memperbaiki mask, ini sangat penting.
- Monitor dengan hati-hati bagaimana topeng Anda berdiri: sebelum atau setelah fungsi aktivasi. Anda mungkin memiliki masalah dengan aktivasi yang tidak sama dengan nol saat argumennya nol (misalnya, sebuah sigmoid).
- Pemangkasan tidak bersahabat dengan batchnorm karena alasan yang sama bahwa putus tidak bersahabat dengan itu: dari sudut pandang normalisasi, ketika ada 32 nilai dalam paket 32 di mana 12 adalah nol, dan ketika 20 nilai dalam paket adalah situasi yang sangat berbeda. Setelah merobek keseimbangan nol, distribusi yang dipelajari oleh lapisan batchnorm tidak lagi valid. Anda harus menyisipkan lapisan pemangkasan setelah semua lapisan batchnorm, atau entah bagaimana memodifikasi yang terakhir.
- Ada juga kesulitan dengan menerapkan pengurangan saluran untuk arsitektur percabangan dan jaringan residual (ResNet). Setelah memangkas neuron ekstra selama penggabungan cabang, dimensi mungkin tidak bersamaan. Ini mudah diselesaikan dengan pengenalan lapisan penyangga, di mana kita tidak menolak neuron. Selain itu, jika cabang jaringan membawa jumlah informasi yang berbeda, masuk akal untuk mengatur yang berbeda lambda sehingga ternyata Pemangkasan tidak hanya memotong semua neuron dalam cabang yang paling tidak informatif. Namun, jika semua neuron dipotong, apakah cabang itu tidak begitu penting?
- Dalam pernyataan asli masalah, ada batasan ketat pada jumlah saluran non-nol, tetapi menurut saya itu cukup untuk mengubah hanya parameter bobot dari kerugian awal dan kehilangan L1 dari bobot penutup, dan kemudian biarkan pengoptimal memutuskan berapa banyak saluran untuk pergi.
- Masker pengambilan. Ini bukan di artikel asli, tetapi menurut saya, ini adalah mekanisme praktis yang baik untuk meningkatkan konvergensi. Ketika nilai topeng mencapai nilai rendah tertentu yang telah ditentukan, kami meresetnya dan melarang mengubah bagian topeng ini. Dengan demikian, bobot yang lemah benar-benar berhenti berkontribusi pada prediksi yang sudah ada selama pelatihan model, dan tidak memasukkan nilai-nilai liar ke dalam jumlah yang sesuai. Secara teoritis, ini dapat mencegah saluran yang berpotensi berguna untuk kembali ke layanan, tetapi saya tidak berpikir bahwa ini sedang terjadi dalam praktik.
Cara yang sulit: regularisasi L0
Tapi kami tidak mencari cara yang mudah, bukan?
Penolakan saluran menggunakan regularisasi L1 tidak sepenuhnya adil. Ini memungkinkan saluran untuk bergerak pada skala "respons kuat" - "respons lemah" - "respons nol". Hanya ketika berat penutup cukup dekat ke nol, kami membuang saluran menggunakan masker penutup. Gerakan seperti itu sangat mendistorsi gambar dan membuat perubahan ke saluran lain selama pelatihan: sebelum mereka dapat belajar apa yang harus dilakukan ketika neuron sebelumnya benar-benar dimatikan, mereka harus belajar apa yang harus dilakukan ketika secara sistematis memberikan respons yang lemah.
Biarkan saya mengingatkan Anda bahwa, idealnya, kami ingin memilih saluran yang paling tidak informatif dari jaringan, terus belajar jaringan tanpa itu, menghapus saluran paling informatif berikutnya, menyesuaikan jaringan lagi, dan sebagainya. Sayangnya, dalam formulasi seperti itu, tugasnya secara komputasi tidak tertahankan bahkan untuk jaringan yang relatif sederhana. Selain itu, pendekatan ini tidak meninggalkan saluran kesempatan kedua - sekali neuron jarak jauh tidak dapat kembali beroperasi lagi. Mari kita ubah tugas sedikit: kita kadang-kadang akan menghapus neuron, dan kadang-kadang meninggalkannya. Selain itu, jika neuron secara keseluruhan bermanfaat, lebih sering dibiarkan, tetapi jika tidak berguna - sebaliknya. Untuk ini, kita akan menggunakan layer masking yang sama seperti dalam kasus regularisasi L1 (bukan tanpa alasan bahwa mereka diperkenalkan!). Hanya bobotnya yang tidak akan bergerak di sepanjang sumbu nyata dengan penarik di nol, tetapi akan terkonsentrasi di sekitar 0 dan 1. Bukannya itu menjadi lebih sederhana, tetapi setidaknya memilah masalah penghapusan neuron secara kategoris.
Naluri pelatih jaringan menunjukkan bahwa tidak perlu menyelesaikan masalah dengan pencarian yang lengkap, tetapi Anda perlu menambahkan jumlah neuron aktif di lapisan pada saat ini berjalan ke fungsi kerugian. Namun, istilah kerugian seperti itu akan konstan bertahap, dan gradient descent tidak dapat bekerja dengannya. Penting untuk mengajarkan algoritma pembelajaran untuk mengecualikan beberapa neuron, meskipun tidak ada gradien.
Kami memiliki cara untuk menghilangkan sementara neuron: kita dapat menerapkan dropout ke layer mask. Biarkan selama pelatihan
betai=1 dengan probabilitas
pi dan
betai=0 dengan probabilitas
1− pi . Sekarang dalam fungsi kerugian, Anda dapat menghitung jumlahnya
pi yang merupakan bilangan real. Di sini kita dihadapkan dengan hambatan lain: distribusinya terpisah, tidak jelas bagaimana backpropagation bekerja dengannya. Secara umum, ada algoritma optimisasi khusus yang dapat membantu kami di sini (lihat REINFORCE), tetapi kami akan mengambil pendekatan yang berbeda.
Dan kemudian tibalah saat di mana
optimasi variasi berperan : kita dapat memperkirakan distribusi diskrit nol dan yang ada di lapisan penutup dengan yang kontinu dan mengoptimalkan parameter yang terakhir menggunakan algoritma backpropagation biasa. Ini adalah ide di balik pekerjaan [Belajar Jarang Jaringan Melalui Lul Regularisasi; Christos Louizos et al; 2017].
Peran distribusi kontinu akan dimainkan oleh distribusi beton keras [Distribusi Beton: Relaksasi Berkelanjutan dari Variabel Acak Acak; Chris Maddison; 2017], berikut ini adalah hal yang rumit dari logaritma yang mendekati distribusi Bernoulli:
alpha - mengimbangi distribusi relatif ke pusat, dan
beta - suhu. Di
beta rightarrow0 distribusi semakin banyak mulai mendekati distribusi Bernoulli yang sebenarnya, tetapi kehilangan diferensiabilitasnya. Di
0< beta<1 kerapatan distribusi cekung (inilah kasus yang kami minati), untuk
beta>1 - cembung. Kami melewati distribusi ini melalui sigmoid yang kaku sehingga dapat dengan terampil memberi dengan probabilitas nol yang terbatas
z=0 dan
z=1 , dan pada interval (0, 1) itu memiliki kepadatan terdiferensiasi terus menerus. Setelah menyelesaikan pemangkasan, kami melihat ke arah mana distribusi telah bergeser dan mengganti variabel acak
z ke nilai topeng tertentu
beta dan kami membawa ke kondisi model yang sudah deterministik.
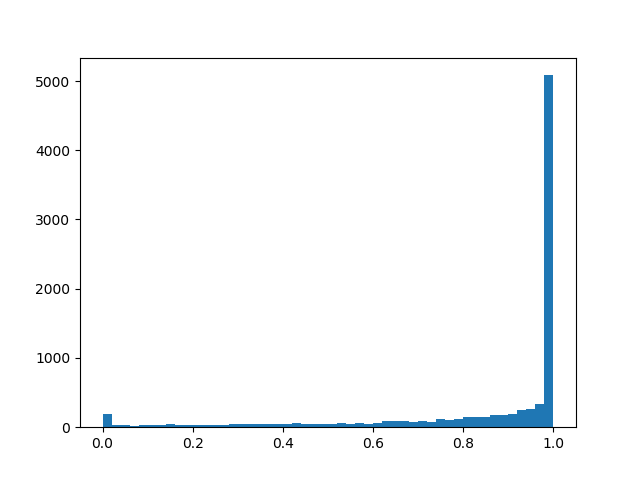
Untuk merasakan distribusi yang sedikit lebih baik, saya akan memberikan beberapa contoh kepadatannya untuk parameter yang berbeda:
Kepadatan distribusi a l p h a = 0 , 0 , b e t a = 0 , 8 :
 a l p h a = 1.0 , b e t a = 0.8
a l p h a = 1.0 , b e t a = 0.8 :
 alpha=2.0, beta=0.8
alpha=2.0, beta=0.8 :
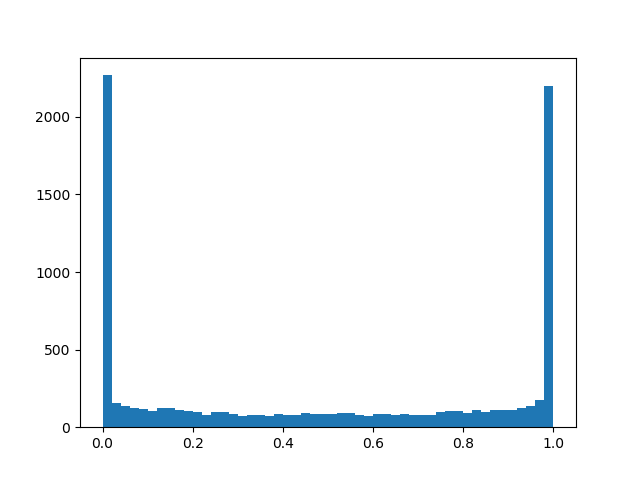
 alpha=0,0, beta=0,5
alpha=0,0, beta=0,5 :
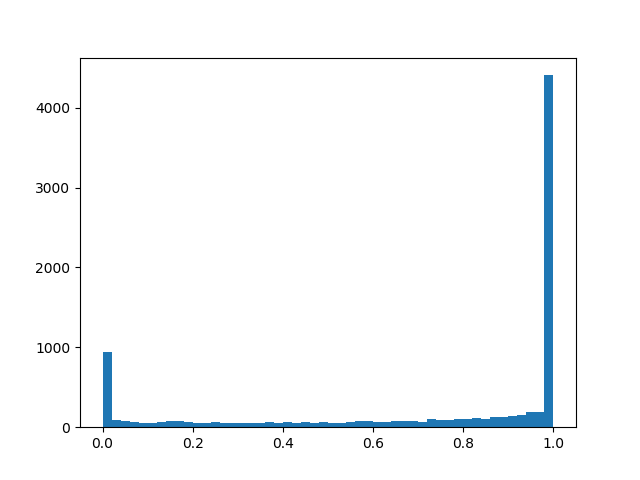
 alpha=1.0, beta=0,5
alpha=1.0, beta=0,5 :
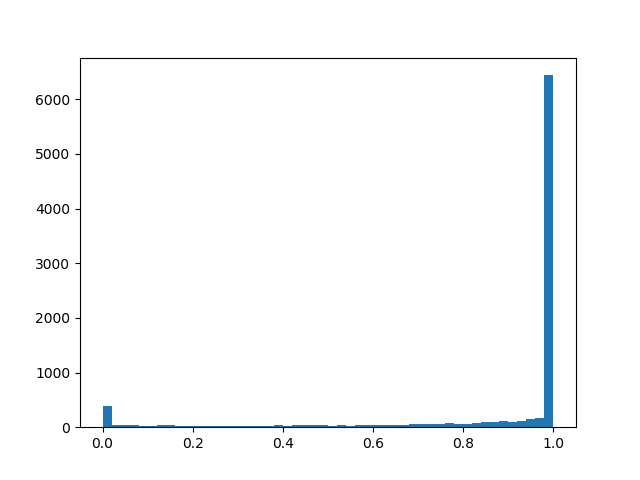
 alpha=2.0, beta=0,5
alpha=2.0, beta=0,5 :
 alpha=2.0, beta=0,1
alpha=2.0, beta=0,1 :
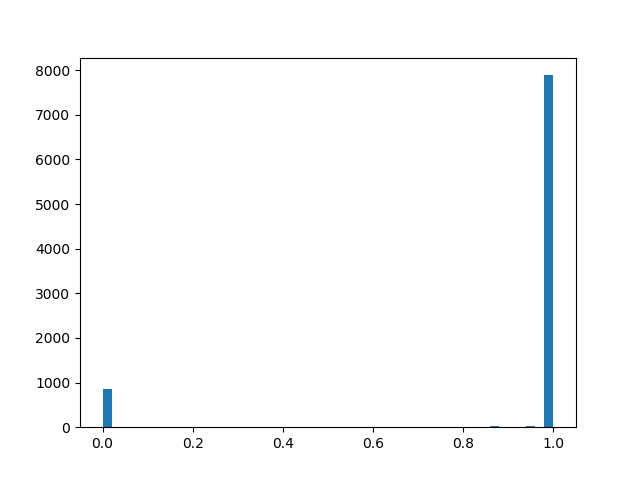 alpha=2.0, beta=2.0
alpha=2.0, beta=2.0 :
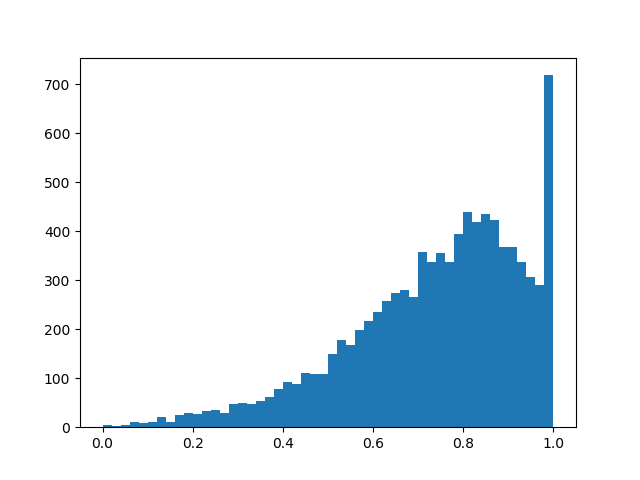
Intinya, kita memiliki layer dropout “pintar” yang mempelajari kesimpulan apa yang harus dibuang lebih sering. Tapi sebenarnya apa yang kita optimalkan? Dalam kerugian, Anda harus meletakkan integral dari kepadatan distribusi di wilayah bukan nol (probabilitas bahwa topeng akan berubah menjadi tidak nol selama pelatihan, cukup cantumkan):
Fitur-fitur berikut ditambahkan ke pelatihan push-pull, regularisasi reguler, dan detail implementasi lainnya yang disebutkan dalam bab tentang regularisasi L1:
- Sekali lagi: lapisan dropout "pintar" kami dengan beberapa probabilitas nyata mengatur ulang output, dengan beberapa - membiarkannya apa adanya, dan ditambah lagi, ada kemungkinan kecil tergantung pada beta, xi, gamma bahwa output akan dikalikan dengan angka acak dari 0 hingga 1. Bagian terakhir lebih parasit daripada berguna untuk tujuan akhir kita, tetapi tanpa itu dengan cara apa pun - diperlukan untuk passback backpropagation'a.
- Umumnya dan alpha dan beta - parameter pelatihan, tetapi dalam percobaan saya, saya merasa bahwa jika Anda hanya bertanya sedikit beta (0,05) dan dalam proses pembelajaran itu masih berkurang secara linear, algoritmanya konvergen lebih baik daripada jika Anda benar-benar mempelajarinya. alpha lebih baik untuk mengatur besar log alpha sekitar2.5 sehingga awalnya neuron lebih sering dipertahankan daripada dibuang, tetapi tidak cukup besar untuk menjenuhkan sigmoid pada loss'e.
- Jika diganti dalam formula log alpha hanya pada alpha seolah-olah jaringan itu konvergen lebih baik dan kecil kemungkinannya mengalami NaN selama pelatihan. Dengan manuver ini, seseorang tidak boleh lupa untuk mengubah istilah dalam fungsi kerugian dan inisialisasi.
- Juga, jika Anda menipu dan mengganti sigmoid biasa di loss'e dengan yang kaku dengan pembatasan log alpha dalam[−4,4] , regularisasi akan lebih baik bertemu dan bertindak lebih kuat.
- Untuk alpha dan beta Anda juga dapat menerapkan regularisasi untuk lebih meningkatkan sparseness.
- Setelah pelatihan, Anda harus membuat hasil binarize dan melatih jaringan secara terus-menerus dengan mask penentu sampai akurasi val mencapai konstan. Artikel ini memberikan formula yang lebih akurat dimana output dari neuron dapat dibuat deterministik selama validasi atau untuk melepaskan jaringan ke rilis, tetapi tampaknya pada akhir pelatihan alpha berubah menjadi cukup terpolarisasi untuk heuristik sederhana untuk bekerja: alpha<0 - topeng 0, alpha geq0 - mask 1 (tapi ini tidak akurat). Setelah pindah ke topeng deterministik, Anda akan melihat lompatan dalam kualitas. Jangan lupa bahwa kami datang ke sini dengan bobot nol, dan di bawah ambang batas berat tertentu, Anda masih perlu mengganti bobot pelindung dengan nol.
- Nilai tambah tambahan dari pendekatan L0 - layer masking mulai bekerja seperti dropout, yang membawa efek pengaturan yang kuat ke jaringan. Tapi ini pedang bermata dua: jika kamu memulai latihan dengan terlalu sedikit alpha Ada risiko merusak struktur jaringan pra-terlatih.
Eksperimennya
Untuk percobaan, ambil dataset CIFAR-10 dan jaringan yang relatif sederhana dari empat lapisan konvolusional, diikuti oleh dua yang sepenuhnya terhubung: Conv2D, Mask, Conv2D, Mask, Pool2D, Conv2D, Mask, Conv2D, Mask, Pool2D, Flatten, Dropout (p = 0,5) , Dense, Mask, Dense (log). Dipercayai bahwa algoritma pemangkasan bekerja lebih baik pada jaringan yang lebih tebal, tetapi di sini saya menemukan masalah teknis murni kurangnya daya komputasi. Sebagai pengoptimal, Adam digunakan dengan tingkat pembelajaran = 0,0015 dan ukuran batch = 32. Selain itu, L1 biasa (0,00005) dan regulasi L2 (0,00025) digunakan. Augmentasi gambar tidak diterapkan. Jaringan dilatih 200 zaman sebelum konvergensi, setelah itu dipertahankan, dan algoritma pengurangan neuron diterapkan untuk itu.
Selain menerapkan algoritma yang dijelaskan di atas untuk pemangkasan, kami menetapkan titik referensi sepele untuk memastikan bahwa algoritma melakukan sesuatu sama sekali. Mari kita coba untuk membuang yang pertama dari setiap layer
k neuron dan menghabisi jaringan yang dihasilkan.
Grafik menunjukkan hasil membandingkan algoritma pengurangan saluran L1 dan L0 setelah serangkaian percobaan dengan konstanta daya regularisasi berbeda. Sumbu x
mewakili persentase pengurangan jumlah
bobot setelah menerapkan algoritma. Pada sumbu Y, keakuratan jaringan potong dalam sampel validasi. Bilah biru di tengah adalah perkiraan kualitas jaringan yang belum terputus neuron. Garis hijau mewakili algoritma pembelajaran topeng L1 sederhana. Garis merah adalah pemangkasan L0. Garis ungu - penghapusan pertama
k saluran. Segitiga hitam - melatih jaringan yang awalnya memiliki bobot lebih sedikit.
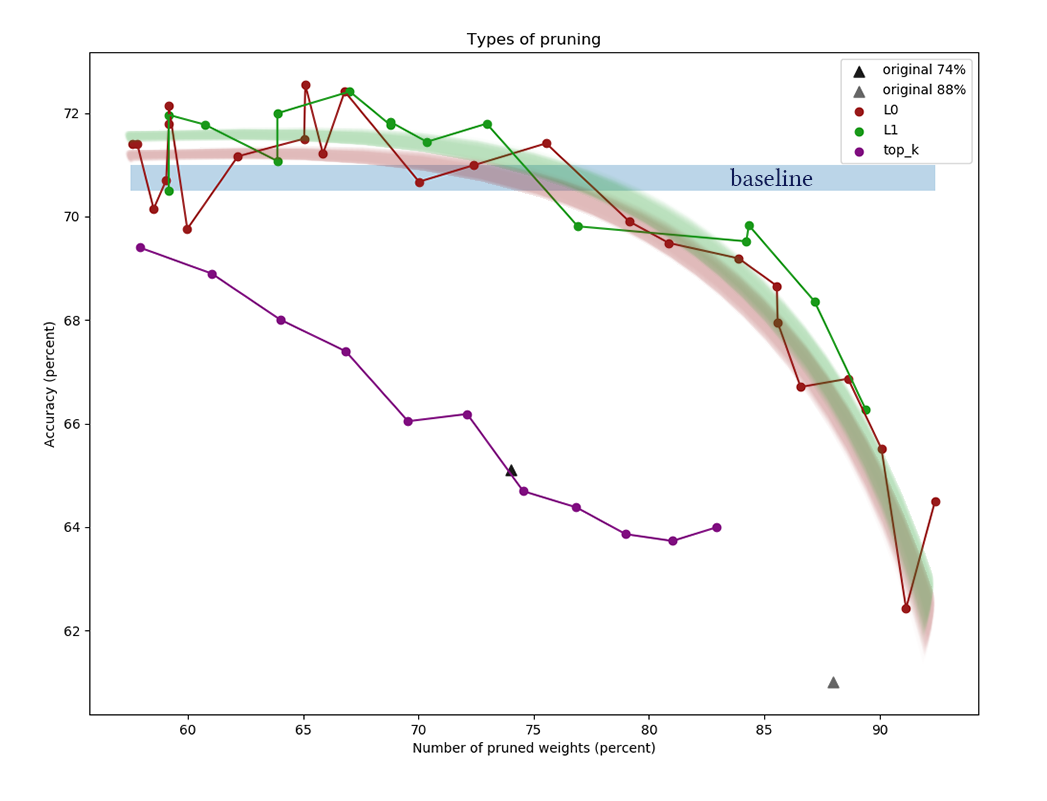
Contoh lain untuk CIFAR-100 dan jaringan yang sedikit lebih panjang dan lebih luas dari arsitektur yang kira-kira sama dan dengan parameter pelatihan yang serupa:
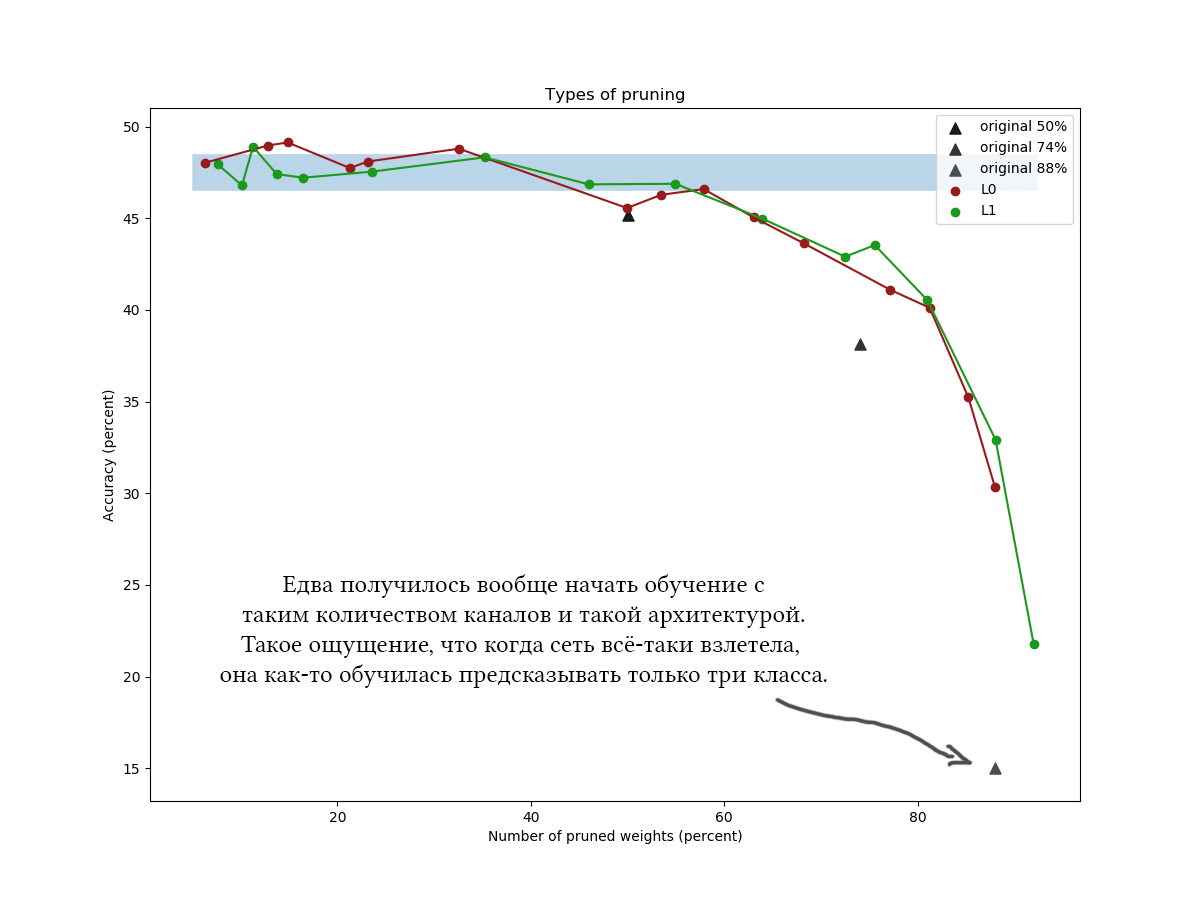
Seperti pada grafik, jelas terlihat bahwa algoritma L1 yang sederhana mengatasi tidak lebih buruk daripada optimasi variasi yang licik, dan tampaknya bahkan meningkatkan kualitas jaringan sedikit lebih banyak pada nilai kompresi yang rendah. Hasilnya juga dikonfirmasi oleh percobaan satu kali dengan dataset lain dan arsitektur jaringan. Ini adalah hasil yang benar-benar diharapkan, yang saya andalkan ketika saya memulai eksperimen pada pengurangan jaringan. Jujur. Huh.
Yah, sejujurnya, saya sedikit terkejut, dan mencoba bermain dengan algoritma dan jaringan: arsitektur yang berbeda, hyperparameter jaringan, formula tepat distribusi beton keras, nilai awal
alpha dan
beta , jumlah zaman tuning menengah. L0-regularisasi terlihat keren secara teori, tetapi dalam praktiknya lebih sulit untuk mengambil hyperparameter, dan itu membutuhkan waktu lebih lama, jadi saya tidak akan merekomendasikan menggunakannya tanpa eksperimen dan pemrosesan file tambahan. Tolong jangan mempertimbangkan waktu yang dihabiskan untuk membaca artikel: Pemangkasan L0 terlihat sangat dapat dipercaya, dan saya akan mengatakan bahwa saya lebih suka menerapkan algoritma di tempat yang salah, bahwa saya tidak menerima keuntungan yang dijanjikan. Plus, pengoptimalan variasi adalah dasar untuk algoritma reduksi yang lebih maju [misalnya, Mengompresi Jaringan Saraf menggunakan Variasi
Informasi Kemacetan, 2018].Secara umum, kesimpulan berikut dapat ditarik:- Banyak saluran di jaringan yang terlatih jelas berlebihan. Bahkan jika Anda menetapkan konstanta regularisasi topeng kecil, mudah untuk mencapai pengurangan bobot 30-50%. Tetapi jika Anda awalnya melatih grid terlalu tipis, sulit untuk mencapai hasil yang baik. Ini berbicara tentang efek menguntungkan dari lapisan lebar pada fungsi target jaringan dan mendukung teori tiket lotre [Hipotesa Tiket Lotere: Pelatihan Jaringan Saraf Tiram, J. Frankle dan M. Carbin, 2018] (semakin banyak neuron, semakin besar kemungkinan bahwa, meskipun jika salah satunya diinisialisasi sehingga membentuk aturan yang baik).
- , . . , ?
- , . 60-90% . k <7%, .
- , (<60%) : , !
- L1 L0 (APoZ), , .. , k .
- , . , , , , . , , . pruning' , . - , .
Ingat bagaimana saya menulis di awal posting bahwa setelah menyelesaikan algoritma prunning, Anda dapat "memotong bagian jaringan sepenuhnya"? Jadi, memotong potongan ekstra jaringan sama sekali tidak mudah. Tensorflow dan perpustakaan lain membangun grafik komputasi, dan itu tidak dapat diubah dengan mudah ketika sudah beroperasi. Anda harus menyimpan jaringan dengan masker yang dihitung, merobek daftar bobot yang diperlukan darinya, mengubah bobot sesuai kebutuhan, menghapus grup yang diberi titik nol, memindahkan kembali, dan membuat jaringan baru berdasarkan set keluaran tensor. Jaringan yang dihasilkan harus memiliki tata letak yang sama seperti aslinya, tetapi akan memiliki lebih sedikit neuron. Harapkan sakit kepala dengan mempertahankan skema jaringan yang sama dalam fungsi menciptakan jaringan awal dan akhir, terutama jika mereka tidak linier, tetapi bercabang.Mungkin untuk penyamaran yang nyaman Anda harus membuat layer Anda sendiri. Ini mudah, tetapi berhati-hatilah dengan koleksi apa yang Anda tambahkan ke opsi masking. Sangat mudah untuk membuat kesalahan dan secara tidak sengaja melatih parameter pengurangan saluran bersama dengan semua skala lainnya.Perlu dicatat bahwa bagian penting dari bobot jaringan dengan arsitektur yang tidak terlalu dalam biasanya terkonsentrasi pada transisi dari bagian konvolusional ke yang terhubung sepenuhnya. Hal ini disebabkan oleh fakta bahwa lapisan konvolusional terakhir dibuat rata, akibatnya, seolah-olah, (jumlah saluran) * (lebar) * (tinggi) neuron terbentuk di dalamnya, dan matriks bobot berikutnya sangat lebar. Bobot ini tidak mungkin dipotong; Selain itu, ini tidak boleh dilakukan, kalau tidak lapisan terakhir jaringan akan "buta" untuk fitur yang ditemukan di beberapa tempat. Dalam kasus seperti itu, cobalah untuk membuat jumlah akhir saluran lebih kecil dan menggunakan maxpool'ing atau bahkan menggunakan arsitektur yang sepenuhnya konvolusional atau terhubung sepenuhnya.Terima kasih atas perhatian Anda, jika seseorang tertarik mengulangi percobaan pada CIFAR-10 dan CIFAR-100,kode dapat diambil di github . Semoga hari kerja Anda menyenangkan!