Pendahuluan

Catatan singkat ini akan berbicara tentang bagaimana model hamburan cahaya atmosfer disusun dalam 4k int terakhir kami Muncul oleh Jetlag , versi partai yang mengambil tempat ke - 12 terhormat di kompo 4k kompo di pesta demo Revisi 2018 pada bulan April tahun ini.

Anda dapat mengunduh biner secara gratis tanpa SMS di sini .

Namun, jika Anda tidak memiliki Windows, atau jika Anda tidak memiliki kartu video modern yang kuat, maka ada orang yang menghibur:

Musik untuk karya ini ditulis oleh tajam menggunakan 4klang . Semua kode dan visual tetap ada di belakangku.

Di sini kita hanya akan berbicara tentang model hamburan cahaya. Hal-hal lain, seperti alat, model kota, model pencahayaan dan material, tidak terpengaruh. Saya dapat mengirim orang-orang pemberani untuk membaca sumbernya , atau menonton rekaman tentang bagaimana saya telah tenggelam selama berjam - jam - sebagian besar pengembangan telah di video.

Sebuah kisah yang membosankan untuk dilewatkan

Pekerjaan pada pekerjaan ini dimulai dengan kesadaran bahwa pekerjaan penuh waktu utama tidak menyisakan waktu untuk bekerja pada pekerjaan 4k penuh - sudah hampir pertengahan Maret di halaman, beberapa minggu tersisa sampai Revizen.
Tetap hanya untuk datang dengan sesuatu yang cukup sederhana untuk cepat, untuk beberapa malam, pengisi kompo. Untuk melakukan pawai ulang yang bodoh tidak berarti menghormati pemirsa, jadi saya ingat bahwa beberapa tahun yang lalu saya harus membuat shader dengan hamburan, dan itu cukup sederhana, padat dan pada saat yang sama diizinkan cantik, walaupun agak lambat.

Dalam suatu diskusi singkat, saya bersikeras pada saya sendiri, dan kami memutuskan untuk fokus pada yang berikut: untuk membuat lanskap yang dipenuhi cahaya yang tersebar, dengan matahari terbenam, awan dan sinar senja (TIL sebagai ungkapan "sinar dewa" diterjemahkan). Agar tidak mengangkat jumlah langkah di atmosfer ke nilai yang benar-benar non-interaktif, Anda harus memutar dengan kuat (seperti metode halaman Monte Carlo), yang akan menghasilkan suara yang terlihat. Tapi itu tidak masalah jika Anda menggerakkan kamera dan mengubah adegan secara perlahan dan memulai trek ambient, Anda dapat dengan mudah mencampur frame yang berdekatan dan untuk sementara memperhalus kebisingan ini.

Keen menulis musik dengan cukup cepat - hampir siap dua minggu sebelum Revisi. Namun, saya benar-benar lumpuh oleh flu - dengan ambulans dan penyakit menular - jadi saya praktis tidak mulai bekerja pada shader sampai saat ketika dalam kondisi hidup yang entah bagaimana saya naik pesawat ke Frankfurt. Prototipe model hamburan ini sudah ditulis di udara.

Kami menyiapkan versi Partai intra dari pasir dan air liur di pesta itu sendiri selama beberapa jam tersisa sebelum batas waktu (dan, mungkin, beberapa setelah; D), sementara saya secara bersamaan pindah dari flu, kurang tidur, penerbangan berjam-jam, dan dia terus-menerus terganggu dengan berpartisipasi dalam kompilasi livecoding showdown Shader .

Versi yang ditampilkan di layar lebar berisi banyak artefak dan hanya geometri dasar kota yang didasarkan pada diagram Voronoi dengan ketinggian acak.

Secara umum, tempat ke-12 cukup murah hati.

Versi terakhir, yang ditunjukkan di atas, dibuat kemudian dan dalam mode yang lebih santai, 1-2 siang seminggu selama sebulan. Secara total, butuh sekitar 40-50 jam kerja untuk bekerja.

Model hamburan

(Catatan: Saya tidak melakukan pemrograman grafis secara profesional. Ini adalah hobi kecil saya untuk kebaikan, jika seratus atau dua sangat tidak fokus di bawah bir jam anggur per tahun. Oleh karena itu, tidak ada kemungkinan nol bahwa beberapa hal dijelaskan di bawah ini dan / atau salah nama. Paman, pukul!)

Model hamburan dipinjam dari artikel "Pencurian Cahaya Outdoor Kinerja Tinggi Menggunakan Epipolar Sampling" oleh Egor Yusov , yang diterbitkan dalam buku GPU Pro 5 , dengan sampel epipolar yang dikeluarkan sepenuhnya.

Model fisik

Foton matahari membombardir atmosfer bumi dan berinteraksi dengan partikel udara. Foton dapat tersebar oleh sebuah partikel, yang memerlukan perubahan arah foton, atau dapat diserap, yang berarti bahwa foton hilang, dan energinya telah diubah menjadi bentuk lain.
Kedua proses adalah probabilistik dan tergantung khususnya pada kepadatan partikel dan energi foton (yang sesuai dengan warnanya).

Di jari, foton "merah" memiliki peluang lebih rendah untuk berinteraksi dengan udara, sehingga foton mengatasi ketebalan atmosfer yang relatif utuh.
Namun yang berwarna biru memiliki kemungkinan hamburan yang lebih tinggi, itulah sebabnya mereka dapat mengubah arah berulang kali dan menempuh jarak yang cukup jauh di atmosfer sebelum mereka mencapai (atau tidak) pengamat.

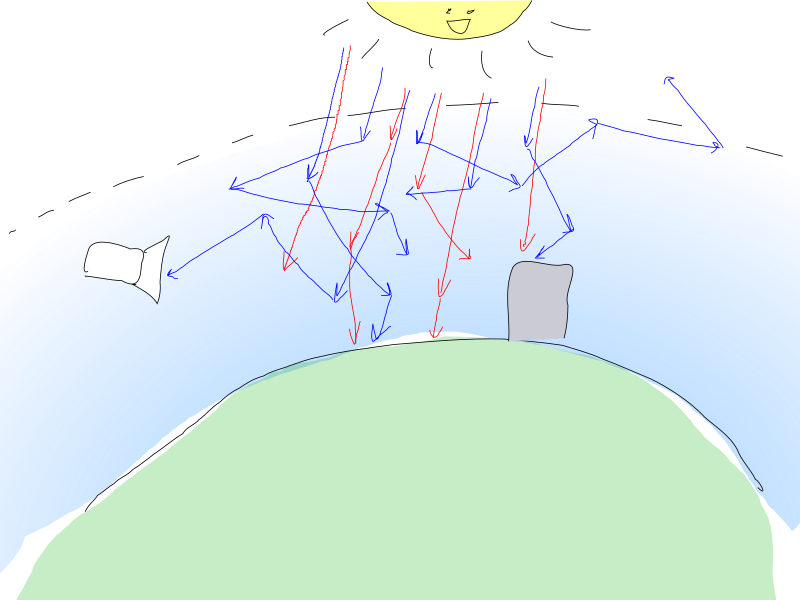
Parameter interaksi cahaya dengan udara yang menarik bagi kami adalah sebagai berikut:

• $$$\ beta ^ s (x)$- Fraksi cahaya yang tersebar per satuan panjang pada suatu titik $$$x$
• $$$\ beta ^ a (x)$- Fraksi cahaya yang diserap per satuan panjang pada suatu titik $$$x$
• $$$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$- total fraksi cahaya yang hilang per satuan panjang pada suatu titik $$$x$
• $$$p (\ alpha)$Apakah distribusi sudut cahaya tersebar, di mana $$$\ alpha$ini adalah sudut antara insiden dan sinar yang tersebar

Diasumsikan bahwa udara terdiri dari dua jenis partikel, hamburan yang terjadi secara independen: molekul (model Rayleigh) dan aerosol (partikel bola yang relatif besar, hamburan Mie dalam literatur bahasa Inggris). Model hanya berbeda dalam nilai yang berbeda untuk parameter di atas.

Untuk kedua model, diyakini bahwa kepadatan partikel yang sesuai berkurang secara eksponensial dengan ketinggian: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$dimana $$$\ rho_0$- Kepadatan di permukaan laut. Peluang $$$\ beta$proporsional $$$\ rho$, dan artinya di bawah ini diberikan untuk permukaan laut.

Model Rayleigh

• $$$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$[Nishita et al. 93, Preetham et al. 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$[Riley et al. 04, Bruneton dan Neyret 08]
• $$$H_R = 7994m$[Nishita et al. 93]

Aerosol

• $$$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alpha)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$[Nisita et al. 93, Riley et al. 04] dimana $$$g = 0,76$[Bruneton dan Neyret 08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$[Bruneton dan Neyret 08]
• $$$\ beta_M ^ e = 1.1 \ beta_M ^ s$
• $$$H_M = 1200m$[Nishita et al. 93]

Perkiraan hamburan tunggal

Perkiraan hamburan didasarkan pada emisi sinar dari setiap piksel kamera dan perhitungan berapa banyak cahaya dari atmosfer yang seharusnya didapat dari arah ini. Setiap sinar sesuai dengan ketiga komponen cahaya RGB, seolah-olah tiga foton dengan energi yang sesuai terbang di sepanjang sinar ini.

Cahaya yang mencapai ruangan dibentuk oleh proses-proses berikut di udara:

• Hamburan (TIL yang ara belajar bagaimana menerjemahkan hamburan). Cahaya yang dipancarkan oleh matahari ditambahkan, yang secara probabilistik tersebar oleh sudut yang sesuai dengan arah ke kamera.
• Penyerapan . Cahaya yang sudah terbang di sepanjang balok diserap oleh udara.
• Hamburan . Cahaya yang sudah terbang di sepanjang balok hilang karena hamburan ke arah lain.

Untuk alasan kinerja, kami percaya bahwa cahaya hanya bisa masuk ke arah kamera dari hamburan sekali, dan semua cahaya lain (yang tersebar lebih dari sekali) dapat diabaikan. Ini tidak disarankan untuk senja, tetapi apa yang harus dilakukan.

Pendekatan ini digambarkan dalam gambar indah berikut (saya mencoba!):

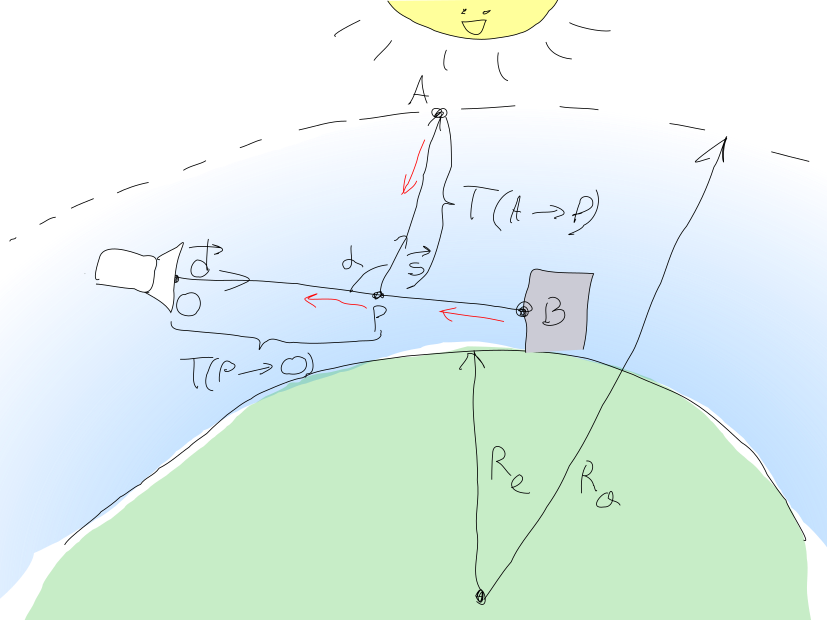
Dengan demikian, jumlah cahaya yang harus dideteksi oleh piksel kamera di $$$O$dapat dihitung sebagai jumlah $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$dimana $$$\ mathbf {L_ {in}}$- Cahaya menyebar dari matahari, dan $$$\ mathbf {L_ {BO}}$- jumlah cahaya dari titik $$$B$objek mencapai adegan geometri $$$O$.

Geometri cahaya

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$dimana $$$\ mathbf {L_O}$Apakah cahaya dipancarkan dari suatu titik $$$B$menuju kamera.

$$$\ mathbf {T} (B \ rightarrow O)$disebut ketebalan optik media antara titik-titik $$$B$dan $$$O$, dan dihitung sebagai berikut:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$$

Sedangkan anggotanya $$$\ beta$terdiri dari konstanta permukaan laut dan kepadatan variabel, ungkapan ini dapat dikonversi menjadi:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$$

Harap dicatat bahwa saya tidak secara khusus mengungkapkan $$$\ rho$, karena kami akan mengubahnya nanti saat menambahkan awan. Saya juga menarik perhatian pada fakta itu $$$\ beta$- Vektor RGB (setidaknya $$$\ mathbf {\ beta_R}$memiliki arti berbeda untuk komponen RGB, dan $$$\ beta_M$- vektor hanya untuk konsistensi). Anggota dengan $$$\ rho$di bawah integral adalah skalar.

Sinar matahari

Sinar matahari $$$\ mathbf {L_ {in}}$dihitung dengan integrasi atas semua titik $$$P$sepanjang segmen $$$Ob$dan akumulasi dari semua sinar matahari yang masuk yang menyebar ke arah kamera dan mati karena ketebalan $$$\ mathbf {T} (P \ rightarrow O)$.

Jumlah sinar matahari mencapai satu titik $$$P$dihitung dengan rumus yang sama $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$dimana $$$\ mathbf {L_ {sun}}$- kecerahan matahari, dan $$$A$Merupakan titik di mana sinar dari titik tersebut $$$P$menuju matahari $$$\ vec {s}$meninggalkan atmosfer. Bagian dari cahaya ini yang akan tersebar ke arah kamera adalah $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$.

Total yang kami dapatkan:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P) \ rightarrow O)} ds$$

Anda mungkin memperhatikan bahwa:

• $$$\ alpha$adalah konstan untuk setiap pixel-ray kamera (kami percaya bahwa matahari jauh sekali dan sinar darinya paralel)
• Peluang $$$\ beta$terdiri dari konstanta permukaan laut dan fungsi kepadatan $$$\ rho (s)$
• Fungsi $$$p (\ alpha)$memiliki faktor umum untuk kedua proses hamburan

Ini memungkinkan Anda untuk mengubah ekspresi menjadi:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1 -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

dimana

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (\) \ rightarrow O)} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (\) \ rightarrow O)} ds$$

$$$I_m$dan $$$I_R$berbeda hanya dalam fungsi kepadatan, eksponensial mereka sama.

Tidak ada yang bisa menghitung integral ini secara analitis, jadi mereka harus dihitung secara numerik menggunakan pemetaan ulang (seperti yang dikatakan dalam publikasi asli, Anda tidak bisa melakukannya!).

Integrasi numerik

Untuk alasan ukuran dan kemalasan, kami akan menganggapnya sebodoh mungkin: $$$\ int_A ^ B f (x) dx \ approx \ frac {\ kiri | B - A \ kanan |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {\ vec { B - A}} {N})$

Ray marching akan dilakukan dalam arah yang berlawanan dengan aliran cahaya: dari titik kamera $$$O$sebelum persimpangan balok dengan geometri $$$B$. Segmen garis $$$O \ rightarrow B$dibagi dengan $$$N$langkah-langkah.

Sebelum memulai pawai, inisialisasi variabel:

• vec2 (dua komponen terpisah, untuk hamburan Rayleigh dan aerosol) total ketebalan optik yang terakumulasi $$$\ mathbf {T_ \ rho} (P) \ rightarrow O)$
• vec3 (RGB) $$$\ mathbf {I_M}$, $$$\ mathbf {I_R}$

Selanjutnya untuk intinya $$$P_i$setiap langkah di antara $$$O$dan $$$B$:

1. Ayo ray $$$\ vec {s}$ke arah matahari dan mendapatkan titik $$$A_i$keluarnya sinar ini dari atmosfer.
2. Hitung ketebalannya $$$\ mathbf {T} (A \ rightarrow P_i)$dengan terlebih dahulu menghitung $$$\ int_A ^ {P_i} \ rho_M (s) ds$dan $$$\ int_A ^ {P_i} \ rho_R (s) ds$menggunakan marching ulang yang sama (dengan jumlah langkah M ), dan kemudian mengalikan istilah yang dihasilkan dengan konstanta yang sesuai $$$\ beta_M ^ e$dan $$$\ mathbf {\ beta_R ^ e}$.
3. Hitung ketebalannya $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. Akumulasi $$$\ mathbf {I_R}$dan $$$\ mathbf {I_M}$menggunakan nilai-nilai ini

Warna akhir setelah reimarching dihitung dengan jumlah persyaratan:

1. Term $$$\ mathbf {L_ {BO}}$dapatkan trivial: variabel yang mengandung $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$mengandung nilai $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$sejak itu $$$P_i$telah mencapai $$$B$.
2. Dengan multiplikasi $$$\ mathbf {I_R}$dan $$$\ mathbf {I_M}$ke konstanta yang sesuai dan dengan menambahkan hasilnya dihitung $$$\ mathbf {L_ {in}}$

Shader

Hamburan sederhana tanpa siapa pun

Menyisir sedikit dan berkomentar sumber hamburan diambil (hampir) langsung dari intra itu sendiri:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

Diam di shader

Awan

Tidak buruk, tetapi gambar seperti itu juga bisa diperoleh dengan lebih mudah dengan tumpukan gradien yang licik.

Dengan cara menipu, mendapatkan awan dan sinar dewa jauh lebih sulit. Mari kita tambahkan.

Idenya adalah untuk memperkirakan awan dengan aerosol dan hanya memodifikasi densitas fungsi densitiesRM() . Ini mungkin tidak benar secara fisik seperti yang kita inginkan (saya tidak tahu bagaimana hamburan cahaya di awan dalam grafik komputer sebenarnya mendekati).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

Bertentangan dengan harapan, kita tidak mendapatkan awan yang indah, kemenangan dan penggemar yang manis, tetapi artefak. Mencoba meningkatkan jumlah langkah artefak di dahi tidak sepenuhnya menghapus, tetapi secara signifikan merusak kinerja.

Solusi kruk yang mendorong intra:

• Artefak paling tidak menyenangkan di cakrawala bersembunyi di balik gunung
• Awan ditambahkan hanya di dekat kamera.
• Monte-Karlovschina ditambahkan, setiap sinar marching digeser dengan offset acak: for (float i = pixel_random.w; i < steps; ++i) . Ini menambah kebisingan yang Anda miliki untuk sementara waktu mulus dengan mencampur frame berturut-turut.

• Jumlah langkah untuk zona yang membutuhkan lebih banyak detail meningkat (misalnya, lapisan dengan awan). Untuk inilah pemisahan fungsi yang tidak masuk akal menjadi scatterImpl() dan scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

Penjajaran dengan geometri adegan

Sebagai hasil pemetaan ulang tradisional dari fungsi jarak dan bayangan, jarak L ke titik B dan warna piksel Lo telah diperoleh. Nilai-nilai ini hanya disubstitusikan ke fungsi scatter() . Jika balok tidak bersandar pada geometri dan meninggalkan tempat kejadian, maka warna Lo nol, dan L dihitung menggunakan escape() - diyakini bahwa balok telah meninggalkan atmosfer.

Suka semuanya.

... Sebenarnya, tentu saja, tidak semua. Sangat menyakitkan untuk menggosok semua bagian sehingga secara keseluruhan terlihat dapat dipercaya. Hanya sekelompok keributan dengan parameter memutar, geometri pemandangan, fungsi noise, lintasan dan sudut kamera. Saya khawatir saya tidak memiliki saran yang baik di sini, kecuali untuk iterating selama berjam-jam dan membenturkan kepala ke dinding.

Minifikasi

Setelah memproses shader minifier , kode sebar shader terakhir berukuran sekitar 1500 byte. Crinkler memampatkannya hingga ~ 700 byte, yang merupakan sekitar 30% dari semua kode shader.

Berkembang biak

Saya tidak tahu cara grafis komputer.