IGNG - Algoritma Incremental Neural Gas Bertambah

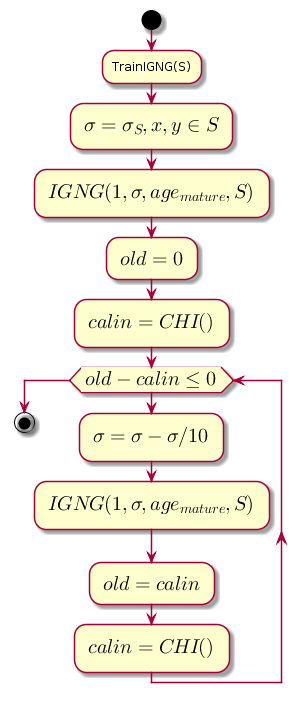
@startuml start :TrainIGNG(S); :<latex>\sigma = \sigma_S,x,y \in S</latex>; :<latex>IGNG(1, \sigma, age_{mature}, S)</latex>; :<latex>old = 0</latex>; :<latex>calin = CHI()</latex>; while (<latex>old - calin \leq 0</latex>) :<latex>\sigma=\sigma - \sigma / 10</latex>; :<latex>IGNG(1, \sigma, age_{mature}, S)</latex>; :<latex>old = calin</latex>; :<latex>calin = CHI()</latex>; endwhile stop @enduml 

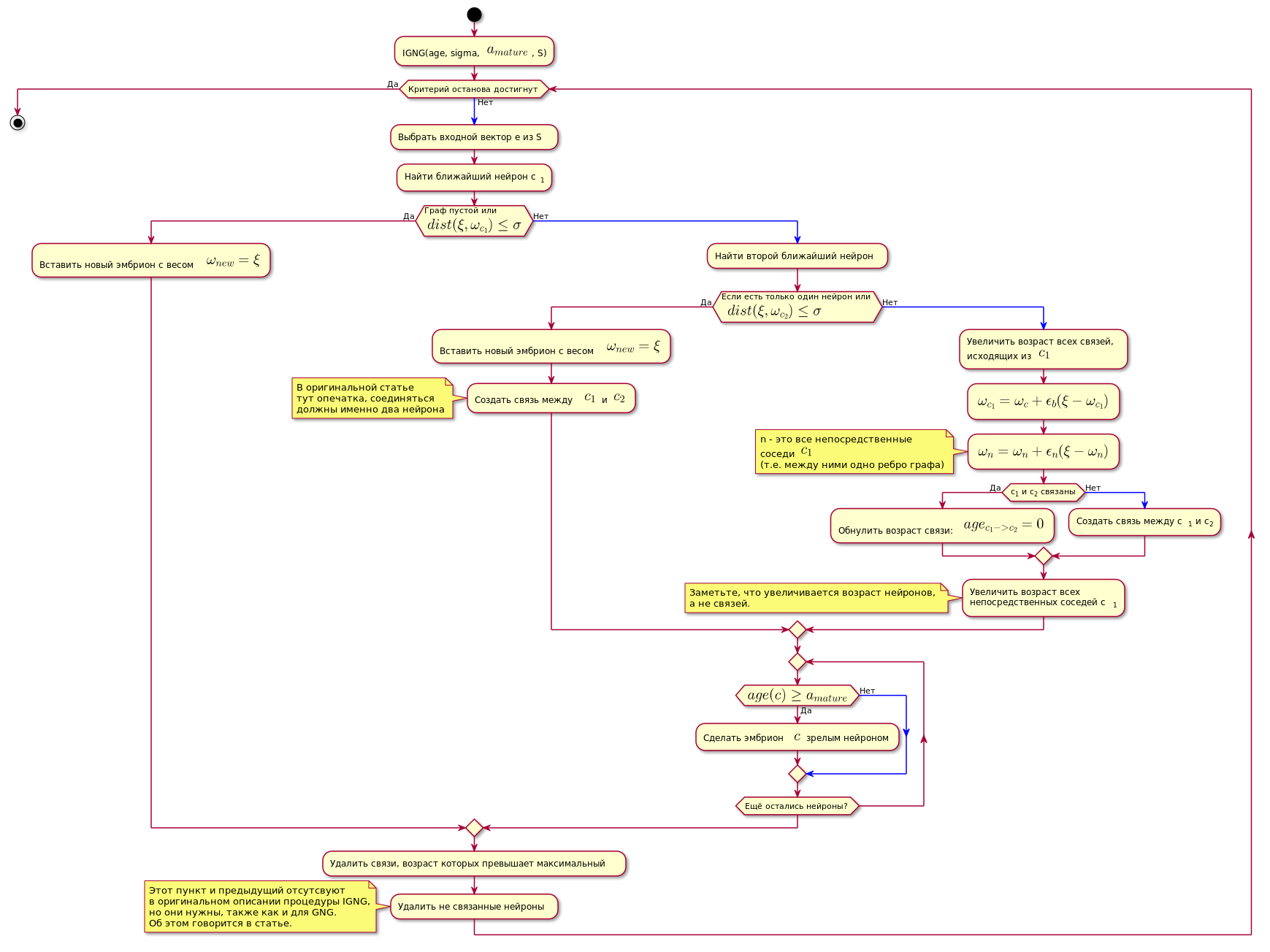
 @startuml skinparam nodesep 10 skinparam ranksep 20 start :IGNG(age, sigma, <latex>a_{mature}</latex>, S); while (  ) is () -[#blue]-> :   e  S; :   c<sub>1</sub>; if (  \n<latex>dist(\xi, \omega_{c_1}) \leq \sigma</latex>) then () :     <latex>\omega_{new} = \xi</latex>; else () -[#blue]-> :   ; if (     \n <latex>dist(\xi, \omega_{c_2}) \leq \sigma</latex>) then () :     <latex>\omega_{new} = \xi</latex>; :   <latex>c_1</latex>  <latex>c_2</latex>; note     ,      end note else () -[#blue]-> :   ,\n  <latex>c_1</latex>; :<latex>\omega_{c_1} = \omega_c + \epsilon_b(\xi - \omega_{c_1})</latex>; :<latex>\omega_n = \omega_n + \epsilon_n(\xi - \omega_n)</latex>; note n -     <latex>c_1</latex> (..     ) end note if (c<sub>1</sub>  c<sub>2</sub> ) then () :  : <latex>age_{c_1 -> c_2} = 0</latex>; else () -[#blue]-> :   c<sub>1</sub>  c<sub>2</sub>; endif :  \n  c<sub>1</sub>; note ,    ,   . end note endif repeat if (<latex>age(c) \geq a_{mature}</latex>) then () :  $<!-- math>c</math -->$  ; else () -[#blue]-> endif repeat while (  ?) endif : ,    ; :   ; note          IGNG,   ,     GNG.     . endnote endwhile () stop @enduml 

 class NeuralGas(): __metaclass__ = ABCMeta def __init__(self, data, surface_graph=None, output_images_dir='images'): self._graph = nx.Graph() self._data = data self._surface_graph = surface_graph # Deviation parameters. self._dev_params = None self._output_images_dir = output_images_dir # Nodes count. self._count = 0 if os.path.isdir(output_images_dir): shutil.rmtree('{}'.format(output_images_dir)) print("Ouput images will be saved in: {0}".format(output_images_dir)) os.makedirs(output_images_dir) self._start_time = time.time() @abstractmethod def train(self, max_iterations=100, save_step=0): raise NotImplementedError() def number_of_clusters(self): return nx.number_connected_components(self._graph) def detect_anomalies(self, data, threshold=5, train=False, save_step=100): anomalies_counter, anomaly_records_counter, normal_records_counter = 0, 0, 0 anomaly_level = 0 start_time = self._start_time = time.time() for i, d in enumerate(data): risk_level = self.test_node(d, train) if risk_level != 0: anomaly_records_counter += 1 anomaly_level += risk_level if anomaly_level > threshold: anomalies_counter += 1 #print('Anomaly was detected [count = {}]!'.format(anomalies_counter)) anomaly_level = 0 else: normal_records_counter += 1 if i % save_step == 0: tm = time.time() - start_time print('Abnormal records = {}, Normal records = {}, Detection time = {} s, Time per record = {} s'. format(anomaly_records_counter, normal_records_counter, round(tm, 2), tm / i if i else 0)) tm = time.time() - start_time print('{} [abnormal records = {}, normal records = {}, detection time = {} s, time per record = {} s]'. format('Anomalies were detected (count = {})'.format(anomalies_counter) if anomalies_counter else 'Anomalies weren\'t detected', anomaly_records_counter, normal_records_counter, round(tm, 2), tm / len(data))) return anomalies_counter > 0 def test_node(self, node, train=False): n, dist = self._determine_closest_vertice(node) dev = self._calculate_deviation_params() dev = dev.get(frozenset(nx.node_connected_component(self._graph, n)), dist + 1) dist_sub_dev = dist - dev if dist_sub_dev > 0: return dist_sub_dev if train: self._dev_params = None self._train_on_data_item(node) return 0 @abstractmethod def _train_on_data_item(self, data_item): raise NotImplementedError() @abstractmethod def _save_img(self, fignum, training_step): """.""" raise NotImplementedError() def _calculate_deviation_params(self, distance_function_params={}): if self._dev_params is not None: return self._dev_params clusters = {} dcvd = self._determine_closest_vertice dlen = len(self._data) #dmean = np.mean(self._data, axis=1) #deviation = 0 for node in self._data: n = dcvd(node, **distance_function_params) cluster = clusters.setdefault(frozenset(nx.node_connected_component(self._graph, n[0])), [0, 0]) cluster[0] += n[1] cluster[1] += 1 clusters = {k: sqrt(v[0]/v[1]) for k, v in clusters.items()} self._dev_params = clusters return clusters def _determine_closest_vertice(self, curnode): """.""" pos = nx.get_node_attributes(self._graph, 'pos') kv = zip(*pos.items()) distances = np.linalg.norm(kv[1] - curnode, ord=2, axis=1) i0 = np.argsort(distances)[0] return kv[0][i0], distances[i0] def _determine_2closest_vertices(self, curnode): """Where this curnode is actually the x,y index of the data we want to analyze.""" pos = nx.get_node_attributes(self._graph, 'pos') l_pos = len(pos) if l_pos == 0: return None, None elif l_pos == 1: return pos[0], None kv = zip(*pos.items()) # Calculate Euclidean distance (2-norm of difference vectors) and get first two indexes of the sorted array. # Or a Euclidean-closest nodes index. distances = np.linalg.norm(kv[1] - curnode, ord=2, axis=1) i0, i1 = np.argsort(distances)[0:2] winner1 = tuple((kv[0][i0], distances[i0])) winner2 = tuple((kv[0][i1], distances[i1])) return winner1, winner2 class IGNG(NeuralGas): """Incremental Growing Neural Gas multidimensional implementation""" def __init__(self, data, surface_graph=None, eps_b=0.05, eps_n=0.0005, max_age=5, a_mature=1, output_images_dir='images'): """.""" NeuralGas.__init__(self, data, surface_graph, output_images_dir) self._eps_b = eps_b self._eps_n = eps_n self._max_age = max_age self._a_mature = a_mature self._num_of_input_signals = 0 self._fignum = 0 self._max_train_iters = 0 # Initial value is a standard deviation of the data. self._d = np.std(data) def train(self, max_iterations=100, save_step=0): """IGNG training method""" self._dev_params = None self._max_train_iters = max_iterations fignum = self._fignum self._save_img(fignum, 0) CHS = self.__calinski_harabaz_score igng = self.__igng data = self._data if save_step < 1: save_step = max_iterations old = 0 calin = CHS() i_count = 0 start_time = self._start_time = time.time() while old - calin <= 0: print('Iteration {0:d}...'.format(i_count)) i_count += 1 steps = 1 while steps <= max_iterations: for i, x in enumerate(data): igng(x) if i % save_step == 0: tm = time.time() - start_time print('Training time = {} s, Time per record = {} s, Training step = {}, Clusters count = {}, Neurons = {}, CHI = {}'. format(round(tm, 2), tm / (i if i and i_count == 0 else len(data)), i_count, self.number_of_clusters(), len(self._graph), old - calin) ) self._save_img(fignum, i_count) fignum += 1 steps += 1 self._d -= 0.1 * self._d old = calin calin = CHS() print('Training complete, clusters count = {}, training time = {} s'.format(self.number_of_clusters(), round(time.time() - start_time, 2))) self._fignum = fignum def _train_on_data_item(self, data_item): steps = 0 igng = self.__igng # while steps < self._max_train_iters: while steps < 5: igng(data_item) steps += 1 def __long_train_on_data_item(self, data_item): """.""" np.append(self._data, data_item) self._dev_params = None CHS = self.__calinski_harabaz_score igng = self.__igng data = self._data max_iterations = self._max_train_iters old = 0 calin = CHS() i_count = 0 # Strictly less. while old - calin < 0: print('Training with new normal node, step {0:d}...'.format(i_count)) i_count += 1 steps = 0 if i_count > 100: print('BUG', old, calin) break while steps < max_iterations: igng(data_item) steps += 1 self._d -= 0.1 * self._d old = calin calin = CHS() def _calculate_deviation_params(self, skip_embryo=True): return super(IGNG, self)._calculate_deviation_params(distance_function_params={'skip_embryo': skip_embryo}) def __calinski_harabaz_score(self, skip_embryo=True): graph = self._graph nodes = graph.nodes extra_disp, intra_disp = 0., 0. # CHI = [B / (c - 1)]/[W / (n - c)] # Total numb er of neurons. #ns = nx.get_node_attributes(self._graph, 'n_type') c = len([v for v in nodes.values() if v['n_type'] == 1]) if skip_embryo else len(nodes) # Total number of data. n = len(self._data) # Mean of the all data. mean = np.mean(self._data, axis=1) pos = nx.get_node_attributes(self._graph, 'pos') for node, k in pos.items(): if skip_embryo and nodes[node]['n_type'] == 0: # Skip embryo neurons. continue mean_k = np.mean(k) extra_disp += len(k) * np.sum((mean_k - mean) ** 2) intra_disp += np.sum((k - mean_k) ** 2) return (1. if intra_disp == 0. else extra_disp * (n - c) / (intra_disp * (c - 1.))) def _determine_closest_vertice(self, curnode, skip_embryo=True): """Where this curnode is actually the x,y index of the data we want to analyze.""" pos = nx.get_node_attributes(self._graph, 'pos') nodes = self._graph.nodes distance = sys.maxint for node, position in pos.items(): if skip_embryo and nodes[node]['n_type'] == 0: # Skip embryo neurons. continue dist = euclidean(curnode, position) if dist < distance: distance = dist return node, distance def __get_specific_nodes(self, n_type): return [n for n, p in nx.get_node_attributes(self._graph, 'n_type').items() if p == n_type] def __igng(self, cur_node): """Main IGNG training subroutine""" # find nearest unit and second nearest unit winner1, winner2 = self._determine_2closest_vertices(cur_node) graph = self._graph nodes = graph.nodes d = self._d # Second list element is a distance. if winner1 is None or winner1[1] >= d: # 0 - is an embryo type. graph.add_node(self._count, pos=copy(cur_node), n_type=0, age=0) winner_node1 = self._count self._count += 1 return else: winner_node1 = winner1[0] # Second list element is a distance. if winner2 is None or winner2[1] >= d: # 0 - is an embryo type. graph.add_node(self._count, pos=copy(cur_node), n_type=0, age=0) winner_node2 = self._count self._count += 1 graph.add_edge(winner_node1, winner_node2, age=0) return else: winner_node2 = winner2[0] # Increment the age of all edges, emanating from the winner. for e in graph.edges(winner_node1, data=True): e[2]['age'] += 1 w_node = nodes[winner_node1] # Move the winner node towards current node. w_node['pos'] += self._eps_b * (cur_node - w_node['pos']) neighbors = nx.all_neighbors(graph, winner_node1) a_mature = self._a_mature for n in neighbors: c_node = nodes[n] # Move all direct neighbors of the winner. c_node['pos'] += self._eps_n * (cur_node - c_node['pos']) # Increment the age of all direct neighbors of the winner. c_node['age'] += 1 if c_node['n_type'] == 0 and c_node['age'] >= a_mature: # Now, it's a mature neuron. c_node['n_type'] = 1 # Create connection with age == 0 between two winners. graph.add_edge(winner_node1, winner_node2, age=0) max_age = self._max_age # If there are ages more than maximum allowed age, remove them. age_of_edges = nx.get_edge_attributes(graph, 'age') for edge, age in iteritems(age_of_edges): if age >= max_age: graph.remove_edge(edge[0], edge[1]) # If it causes isolated vertix, remove that vertex as well. #graph.remove_nodes_from(nx.isolates(graph)) for node, v in nodes.items(): if v['n_type'] == 0: # Skip embryo neurons. continue if not graph.neighbors(node): graph.remove_node(node) def _save_img(self, fignum, training_step): """.""" title='Incremental Growing Neural Gas for the network anomalies detection' if self._surface_graph is not None: text = OrderedDict([ ('Image', fignum), ('Training step', training_step), ('Time', '{} s'.format(round(time.time() - self._start_time, 2))), ('Clusters count', self.number_of_clusters()), ('Neurons', len(self._graph)), (' Mature', len(self.__get_specific_nodes(1))), (' Embryo', len(self.__get_specific_nodes(0))), ('Connections', len(self._graph.edges)), ('Data records', len(self._data)) ]) draw_graph3d(self._surface_graph, fignum, title=title) graph = self._graph if len(graph) > 0: draw_graph3d(graph, fignum, clear=False, node_color=(1, 0, 0), title=title, text=text) mlab.savefig("{0}/{1}.png".format(self._output_images_dir, str(fignum))) #mlab.close(fignum)