🥀 👓 💽 Model Regresi Polinomial 🕺🏻 💪🏾 🍸

Secara sederhana, model regresi dalam statistik matematika dibangun berdasarkan data yang diketahui, yang merupakan pasangan angka. Jumlah pasangan demikian sudah ditentukan sebelumnya. Jika Anda membayangkan bahwa angka pertama dalam pasangan adalah nilai koordinat $x$ dan yang kedua $y$ , maka himpunan pasangan angka tersebut dapat direpresentasikan pada bidang dalam sistem koordinat Cartesian sebagai himpunan poin. Pasangan angka ini tidak diambil secara acak. Dalam praktiknya, sebagai aturan, angka kedua tergantung pada yang pertama. Membangun regresi berarti mengambil garis tersebut (lebih tepatnya, fungsi) yang sedekat mungkin (mendekati) banyak poin di atas.

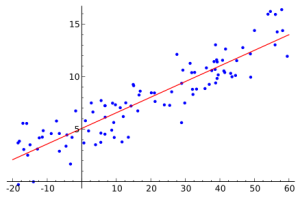
Untuk apa semua ini? Pertama-tama, ini diperlukan untuk persiapan apa yang disebut perkiraan. Seringkali perlu mencari tahu

y

$y$ hanya mengetahui

x

$x$ jika berbeda dari X tersebut, atas dasar mana regresi dibangun. Saya akan memberikan contoh sederhana. Ada statistik tentang ketergantungan pertumbuhan seseorang pada usianya berdasarkan pada 100 orang berbeda yang dipelajari. Dengan demikian, kami memiliki 100 pasang angka {umur; pertumbuhan}. Pada saat yang sama, "pertumbuhan" adalah kuantitas yang tergantung, dan "usia" adalah independen. Dengan membangun model regresi dengan benar, kita dapat "memprediksi" pertumbuhan dengan kepastian apa pun berdasarkan nilai usia.

Dalam praktiknya, tergantung pada situasinya, linier, parabola, kekuasaan, dan jenis fungsi lainnya digunakan dalam pembuatan model regresi. Dalam perjalanan statistik matematika, model regresi linier paling sering dipertimbangkan. Kadang-kadang mereka menyentuh kasus yang lebih rumit - model parabola. Membuat generalisasi, mudah ditebak bahwa model linier dan parabola adalah kasus-kasus tertentu dari model yang lebih kompleks - polinomial. Membangun model regresi berarti menemukan parameter fungsi yang akan muncul di dalamnya. Untuk regresi linier - dua parameter: koefisien dan istilah bebas.

Regresi polinomial dapat digunakan dalam statistik matematika untuk memodelkan komponen tren deret waktu. Rangkaian waktu sebenarnya adalah serangkaian angka yang bergantung pada waktu. Misalnya, suhu harian rata-rata selama setahun terakhir, atau pendapatan bulanan perusahaan. Urutan polinomial yang disimulasikan dievaluasi dengan metode khusus, misalnya, dengan kriteria seri. Tujuan membangun model regresi polinomial di bidang deret waktu masih sama - perkiraan.

Untuk mulai dengan, kami mempertimbangkan masalah regresi polinom secara umum. Semua penalaran didasarkan pada generalisasi penalaran dalam masalah regresi linier dan parabola. Setelah pertimbangan ini, saya akan beralih ke kasus khusus - pertimbangan model ini untuk deret waktu.

Biarkan dua seri pengamatan diberikan $x_i$ (variabel independen) dan $y_i$ (variabel dependen) $i = \ overline {1, n}$ . Persamaan polinomial memiliki bentuk

y = j u m l a h l i m i t_{j = 0}^{k} b_{j} x^{j}, (1)

$y = \ jumlah \ limit_ {j = 0} ^ k b_jx ^ j, \ \ \ \ \ (1)$

dimana

b_{j}

$b_j$ - parameter dari polinomial ini,

j = o v e r l i n e 0, k

$j = \ overline {0, k}$ . Di antara mereka

b_{0}

$b_0$ - anggota gratis. Mari kita cari parameter kuadrat terkecil (OLS)

b_{j}

$b_j$ diberikan regresi.

Dengan analogi dengan regresi linier, OLS juga didasarkan pada meminimalkan ekspresi berikut:

S = j u m l a h l i m i t_{i = 1}^{n} k i r i (h a t y_{i} - y_{i} k a n a n)^{2} t o m i n (2)

$S = \ jumlah \ limit_ {i = 1} ^ n \ kiri (\ hat y_i-y_i \ kanan) ^ 2 \ to \ min \ \ \ \ \ (2)$

Di sini $\ hat y_i$ - Nilai teoritis yang merupakan nilai polinomial (1) pada titik $x_i$ . Mengganti (1) dalam (2), kita dapatkan

S = j u m l a h l i m i t_{i = 1}^{n} k i r i (s u m_{j = 0}^{k} b_{j} x_{i}^{j} - y_{i} k a n a n)^{2} h i n g g a m n t

$S = \ jumlah \ limit_ {i = 1} ^ n \ kiri (\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ kanan) ^ 2 \ hingga \ mnt$

Berdasarkan kondisi yang diperlukan untuk fungsi ekstrem $(k + 1)$ variabel $S = S (b_0, b_1, \ dots, b_k)$ kami menyamakan turunan parsialnya menjadi nol, mis.

S_{b_{p}}^{'} = 2 j u m l a h l i m i t_{i = 1}^{n} x_{i}^{p} k i r i (j u m l a h l i m i t_{j = 0}^{k} b_{j} x_{i}^{j} - y_{i} k a n a n) = 0, p = o v e r l i n e 0, k .

$S '_ {b_p} = 2 \ jumlah \ limit_ {i = 1} ^ nx_i ^ p \ kiri (\ jumlah \ limit_ {j = 0} ^ kb_jx_i ^ j-y_i \ kanan) = 0, \ \ \ p = \ overline {0, k}.$

Membagi sisi kiri dan kanan masing-masing persamaan dengan 2, kami mengungkapkan jumlah kedua:

j u m l a h l i m i t_{i = 1}^{n} x_{i}^{p} k i r i (b_{0} + b_{1} x_{i} + b_{2} x_{i}^{2} + t i t i k + b_{k} x_{i}^{k} k a n a n) - j u m l a h l i m i t_{i = 1}^{n} x_{i}^{p} y_{i} = 0, p = o v e r l i n e 0, k .

$\ jumlah \ limit_ {i = 1} ^ nx_i ^ p \ kiri (b_0 + b_1x_i + b_2x_i ^ 2 + \ titik + b_kx_i ^ k \ kanan) - \ jumlah \ limit_ {i = 1} ^ nx_i ^ py_i = 0 , \ \ \ p = \ overline {0, k}.$

Membuka kurung, kami transfer di masing-masing

p

$p$ Ekspresi th, istilah terakhir dengan

y_{i}

$y_i$ ke kanan dan membagi kedua belah pihak dengan

n

$n$ . Hasilnya, kami dapat

(k + 1)

$(k + 1)$ ekspresi membentuk sistem persamaan normal linier untuk

b_{p}

$b_p$ . Ini memiliki bentuk berikut:

\ left \ {\ begin {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ overline {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {array} \ benar. \ \ \ \ \ (3)

$\ left \ {\ begin {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ overline {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {array} \ benar. \ \ \ \ \ (3)$

Anda dapat menulis ulang sistem (3) dalam bentuk matriks: $AB = C$ dimana

A = \ kiri (\ begin {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ overline {x ^ 2 } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} & \ overline {x ^ 3} & \ overline {x ^ 4} & & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ \ overline {x ^ k} & \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {array} \ kanan), \ \ B = \ kiri (\ begin {array} {c} b_0 \\ b_1 \\ b_2 \\ vdots \\ b_k \ end {array} \ kanan), \ \ C = \ kiri (\ begin {array} {c} \ overline y \\ overline {xy} \\ \ overline {x ^ 2thn} \\ vdots \ overline {x ^ ky} \ end {array} \ kanan).

$A = \ kiri (\ begin {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ overline {x ^ 2 } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} & \ overline {x ^ 3} & \ overline {x ^ 4} & & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ \ overline {x ^ k} & \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {array} \ kanan), \ \ B = \ kiri (\ begin {array} {c} b_0 \\ b_1 \\ b_2 \\ vdots \\ b_k \ end {array} \ kanan), \ \ C = \ kiri (\ begin {array} {c} \ overline y \\ overline {xy} \\ \ overline {x ^ 2thn} \\ vdots \ overline {x ^ ky} \ end {array} \ kanan).$

Sekarang kita beralih ke penerapan fakta-fakta di atas dalam kasus deret waktu. Biarkan deret waktu diberikan $x_t$ dimana $t = \ overline {1, n}$ . Diperlukan untuk membangun tren urutan polinomial $k$ , yang mendekati deret waktu yang diberikan seakurat mungkin. Sebagai variabel independen $x$ kami akan mengambil $t$ berdasarkan definisi deret waktu. Xs ini adalah serangkaian bilangan asli yang menunjukkan periode waktu. Sebagai a $y$ nilai seri waktu diambil $x_t$ . Dapat dilihat bahwa nilai-nilai elemen $a_ {ij}$ matriks sistem $A$ independen dari $x_t$ . Karena dalam kasus umum, jelas,

a_{i j} = o v e r l i n e x^{i + j - 2} = f r a c 1 n j u m l a h l i m i t_{r = 1}^{n} x_{r}^{i + j - 2},

$a_ {ij} = \ overline {x ^ {i + j-2}} = \ frac1n \ jumlah \ limit_ {r = 1} ^ nx_r ^ {i + j-2},$

kemudian dalam hal deret waktu

a_{i j} = f r a c 1 n j u m l a h l i m i t_{r = 1}^{n} r^{i + j - 2},

$a_ {ij} = \ frac1n \ jumlah \ limit_ {r = 1} ^ nr ^ {i + j-2},$

dimana

i, j = o v e r l i n e 1, (k + 1) .

$i, j = \ overline {1, (k + 1)}.$

Item $c_j$ vektor matriks istilah gratis $C$ umumnya diperoleh sebagai

c_{j} = o v e r l i n e x^{j - 1} y = f r a c 1 n j u m l a h l i m i t_{r = 1}^{n} x_{r}^{j - 1} y_{r} .

$c_j = \ overline {x ^ {j-1} y} = \ frac1n \ jumlah \ limit_ {r = 1} ^ nx_r ^ {j-1} y_r.$

Dan dalam hal deret waktu

c_{j} = f r a c 1 n j u m l a h l i m i t_{r = 1}^{n} r^{j - 1} x_{r},

$c_j = \ frac1n \ jumlah \ limit_ {r = 1} ^ nr ^ {j-1} x_r,$

dimana

j = o v e r l i n e 1, (k + 1) .

$j = \ overline {1, (k + 1)}.$

Dengan demikian, setelah menyelesaikan sistem (3), kita dapat menemukan parameter yang diinginkan dari tren polinomial $b_0, \ dots, b_k.$

Untuk mengisi matriks sistem dan menyelesaikannya, salah satu metode numerik dapat digunakan saat memodelkan tren pada komputer. Dalam hal ini, hasil perhitungan akan cukup akurat.

Akibatnya, komponen tren akan berbentuk:

T_{t} = j u m l a h l i m i t_{i = 0}^{k} b_{i} t^{i}, t = 0, 1, 2, d o t s .

$T_t = \ jumlah \ limit_ {i = 0} ^ kb_it ^ i, \ \ \ t = 0,1,2, \ dots.$

Perlu dicatat juga bahwa komponen tren yang disimulasikan

T_{t}

$T_t$ , ditentukan tidak hanya untuk periode saat ini

[1; n]

$[1; n]$ , tetapi juga untuk periode mendatang

t > n

$t> n$ .

Saya segera mencatat bahwa model regresi polinomial hanya komponen tren dari deret waktu. Model deret waktu lengkap juga menyiratkan komponen lain, yang berada di luar cakupan artikel ini.

Dalam praktiknya, saya pribadi belum melihat deret waktu dengan urutan tren polinomial lebih dari 2. Ini menjelaskan prevalensi model regresi linier dan prabolik sebagai kasus polinomial tertentu.

Model Regresi Polinomial

More articles: