Jika Anda menjelaskan dalam beberapa kalimat tentang prinsip pertukaran sorting apa yang berfungsi, maka:

1. Elemen array dibandingkan berpasangan
2. Jika elemen di sebelah kiri ^* lebih besar dari elemen di sebelah kanan, maka elemen tersebut ditukar
3. Ulangi langkah 1-2 hingga array diurutkan

^{* - elemen di sebelah kiri berarti elemen dari pasangan yang dibandingkan, yang lebih dekat ke tepi kiri array. Dengan demikian, elemen di sebelah kanan lebih dekat ke tepi kanan.}

Saya segera minta maaf karena mengulangi materi terkenal, tidak mungkin bahwa setidaknya satu dari algoritma dalam artikel akan menjadi wahyu untuk Anda. Tentang pengurutan ini di Habré sudah ditulis berkali-kali (termasuk saya - 1 , 2 , 3 ) dan bertanya mengapa lagi untuk kembali ke topik ini? Tetapi karena saya memutuskan untuk menulis serangkaian artikel yang koheren tentang semua penyortiran di dunia , saya harus melalui metode pertukaran bahkan dalam versi kilat. Ketika mempertimbangkan kelas-kelas berikut, sudah akan ada banyak algoritma baru (dan sedikit orang yang tahu) yang pantas mendapatkan artikel menarik yang terpisah.

Secara tradisional, "penukar" termasuk penyortiran di mana elemen berubah (semu) secara acak (bogosort, bozosort, permsort, dll.). Namun, saya tidak memasukkan mereka ke dalam kelas ini, karena mereka tidak memiliki perbandingan. Akan ada artikel terpisah tentang penyortiran ini, di mana kami banyak berfilsafat tentang teori probabilitas, kombinatorik, dan kematian termal Semesta.

Sortir Konyol :: Urut antek

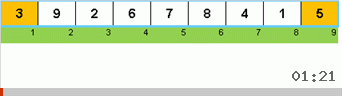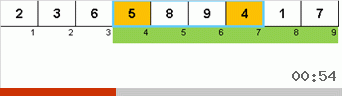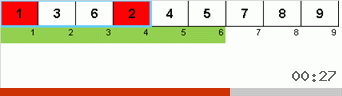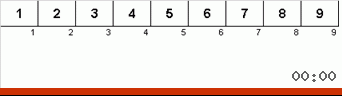
1. Bandingkan (dan jika perlu ubah) elemen-elemen di ujung subarray.
2. Kami mengambil dua pertiga dari subarray dari awal dan menerapkan algoritma umum untuk 2/3 ini secara rekursif.
3. Kami mengambil dua pertiga dari subarray dari ujungnya dan menerapkan algoritma umum untuk 2/3 ini secara rekursif.
4. Dan lagi, kita mengambil dua pertiga dari subarray dari awal dan menerapkan algoritma umum untuk 2/3 ini secara rekursif.

Awalnya, sebuah subarray adalah seluruh array. Dan kemudian rekursi membagi subarray induk menjadi 2/3, membuat perbandingan / pertukaran di ujung segmen yang terfragmentasi, dan akhirnya mengatur semuanya.

def stooge_rec(data, i = 0, j = None): if j is None: j = len(data) - 1 if data[j] < data[i]: data[i], data[j] = data[j], data[i] if j - i > 1: t = (j - i + 1) // 3 stooge_rec(data, i, j - t) stooge_rec(data, i + t, j) stooge_rec(data, i, j - t) return data def stooge(data): return stooge_rec(data, 0, len(data) - 1) 

Kelihatannya skizofrenik, tetapi 100% benar.

Sortir Lambat :: Sortir lambat

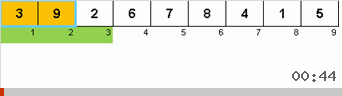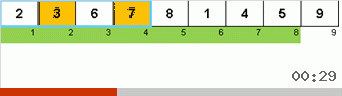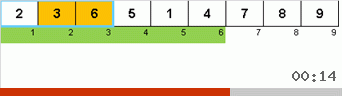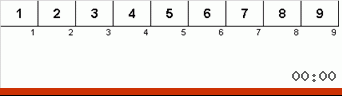
Dan di sini kita amati mistisisme rekursif:

1. Jika subarray terdiri dari satu elemen, maka kami menyelesaikan rekursi.
2. Jika sebuah subarray terdiri dari dua atau lebih elemen, maka bagi menjadi dua.
3. Kami menerapkan algoritma secara rekursif ke bagian kiri.
4. Kami menerapkan algoritma secara rekursif ke bagian kanan.
5. Elemen di ujung subarray dibandingkan (dan diubah jika perlu).
6. Kami menerapkan algoritma secara rekursif ke subarray tanpa elemen terakhir.

Awalnya, sebuah subarray adalah seluruh array. Dan rekursi akan terus membelah dua, membandingkan dan mengubah sampai semuanya beres.

 def slow_rec(data, i, j): if i >= j: return data m = (i + j) // 2 slow_rec(data, i, m) slow_rec(data, m + 1, j) if data[m] > data[j]: data[m], data[j] = data[j], data[m] slow_rec(data, i, j - 1) def slow(data): return slow_rec(data, 0, len(data) - 1) 

Ini terlihat seperti omong kosong, tetapi array tersebut dipesan.

Mengapa StoogeSort dan SlowSort berfungsi dengan benar?

Seorang pembaca yang ingin tahu akan mengajukan pertanyaan yang masuk akal: mengapa kedua algoritma ini bekerja? Mereka tampaknya sederhana, tetapi tidak terlalu jelas bahwa Anda dapat mengurutkan sesuatu seperti itu.

Pertama mari kita lihat pada Slow sort. Poin terakhir dari algoritma ini mengisyaratkan bahwa upaya pengurutan lamban yang rekursif hanya ditujukan untuk menempatkan elemen terbesar dalam subarray di posisi paling kanan. Ini terutama terlihat jika Anda menerapkan algoritma ke array yang dipesan kembali:



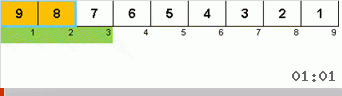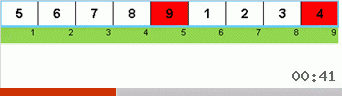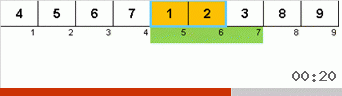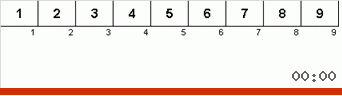
Terlihat jelas bahwa pada semua tingkat rekursi, maxima dengan cepat bermigrasi ke kanan. Kemudian maxima ini, di mana mereka diperlukan, dimatikan dari permainan: algoritma memanggil dirinya sendiri - tetapi tanpa elemen terakhir.

Dalam semacam Stooge, sihir yang sama terjadi:



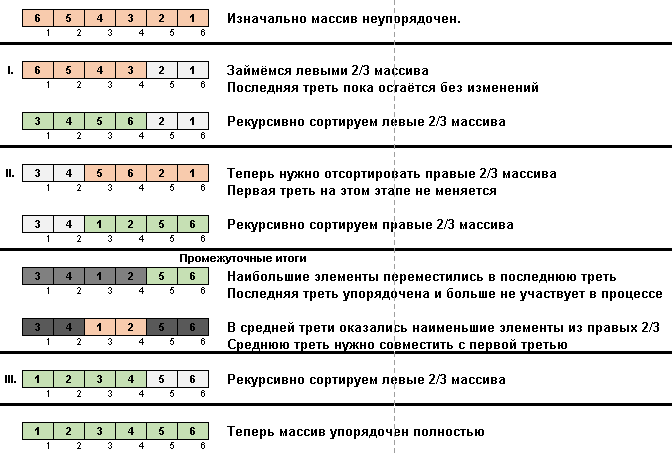
Bahkan, penekanan juga diberikan pada elemen maksimal. Hanya Slow sort yang menggerakkan mereka ke ujung satu per satu, dan Stooge sort mendorong sepertiga elemen dari subarray (yang terbesar dari mereka) mendorong ke sepertiga paling kanan dari ruang sel.

Kami beralih ke algoritma, di mana semuanya sudah cukup jelas.

Sortir Bodoh :: Sortir bodoh

Penyortiran sangat hati-hati. Ia pergi dari awal array ke akhir dan membandingkan elemen tetangga. Jika dua elemen tetangga harus dipertukarkan, maka, untuk berjaga-jaga, menyortir kembali ke awal array dan mulai dari awal lagi.

 def stupid(data): i, size = 1, len(data) while i < size: if data[i - 1] > data[i]: data[i - 1], data[i] = data[i], data[i - 1] i = 1 else: i += 1 return data 

Gnome sort :: Gnome sort

Hampir hal yang sama, tetapi menyortir selama pertukaran tidak kembali ke awal array, tetapi hanya mengambil satu langkah mundur. Ternyata, ini sudah cukup untuk menyelesaikan semuanya.

 def gnome(data): i, size = 1, len(data) while i < size: if data[i - 1] <= data[i]: i += 1 else: data[i - 1], data[i] = data[i], data[i - 1] if i > 1: i -= 1 return data 

Sortir Kurcaci yang Dioptimalkan

Tetapi Anda dapat menghemat tidak hanya pada retret, tetapi juga saat bergerak maju. Dengan beberapa pertukaran berturut-turut, Anda harus mengambil langkah mundur sebanyak mungkin. Dan kemudian Anda harus kembali (membandingkan sepanjang jalan elemen yang sudah dipesan relatif satu sama lain). Jika Anda ingat posisi dari mana pertukaran dimulai, maka Anda dapat langsung melompat ke posisi ini ketika pertukaran selesai.

 def gnome(data): i, j, size = 1, 2, len(data) while i < size: if data[i - 1] <= data[i]: i, j = j, j + 1 else: data[i - 1], data[i] = data[i], data[i - 1] i -= 1 if i == 0: i, j = j, j + 1 return data 

Bubble Sort :: Bubble sort

Tidak seperti penyortiran bodoh dan gnomeish, ketika bertukar elemen dalam gelembung, tidak ada pengembalian terjadi - itu terus bergerak maju. Mencapai akhir, elemen terbesar dari array dipindahkan ke bagian paling akhir.

Kemudian proses penyortiran mengulangi seluruh proses lagi, sebagai hasilnya elemen kedua dalam senioritas berada di tempat terakhir tetapi satu. Pada iterasi berikutnya, elemen terbesar ketiga adalah elemen ketiga dari akhir, dll.

 def bubble(data): changed = True while changed: changed = False for i in range(len(data) - 1): if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] changed = True return data 

Sortir Bubble yang Dioptimalkan

Anda bisa mendapat sedikit manfaat di gang-gang di awal array. Dalam prosesnya, elemen pertama dipesan sementara untuk relatif satu sama lain (bagian yang diurutkan ini terus-menerus berubah ukuran - berkurang, meningkat). Ini mudah diperbaiki dan dengan iterasi baru Anda cukup melompati sekelompok elemen tersebut.
_{(Saya akan menambahkan implementasi yang diuji dengan Python di sini sebentar lagi. Saya tidak punya waktu untuk mempersiapkannya.)}

Shaker Sort :: Shaker Sort
(Sortir koktail :: Semacam koktail)

Semacam gelembung. Pada operan pertama, seperti biasa - dorong maksimal ke ujung. Lalu kami dengan tajam berbalik dan mendorong minimum ke awal. Area marginal yang disortir dari array bertambah besar setelah setiap iterasi.

 def shaker(data): up = range(len(data) - 1) while True: for indices in (up, reversed(up)): swapped = False for i in indices: if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] swapped = True if not swapped: return data 

Sorting ganjil :: Ganjil genap

Lagi iterasi atas perbandingan berpasangan dari elemen tetangga ketika bergerak dari kiri ke kanan. Hanya pertama, bandingkan pasangan di mana elemen pertama aneh dalam penghitungan, dan yang kedua adalah genap (yaitu, yang pertama dan kedua, ketiga dan keempat, kelima dan keenam, dll). Dan sebaliknya - bahkan + ganjil (kedua dan ketiga, keempat dan kelima, keenam dan ketujuh, dll.). Dalam hal ini, banyak elemen besar array pada satu iterasi pada saat yang sama mengambil satu langkah maju (dalam gelembung, yang terbesar untuk iterasi mencapai akhir, tetapi sisanya yang agak besar hampir tetap di tempatnya).

By the way, ini awalnya semacam paralel dengan kompleksitas O (n). Penting untuk mengimplementasikan AlgoLab di bagian "Penyortiran Paralel".

 def odd_even(data): n = len(data) isSorted = 0 while isSorted == 0: isSorted = 1 temp = 0 for i in range(1, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 for i in range(0, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 return data 

Comb Sort :: Comb sort

Modifikasi gelembung paling sukses. Algoritma kecepatan bersaing dengan pengurutan cepat.

Di semua variasi sebelumnya, kami membandingkan tetangga. Dan di sini, pertama, pasangan elemen dianggap berada pada jarak maksimum satu sama lain. Pada setiap iterasi baru, jarak ini menyempit secara seragam.

 def comb(data): gap = len(data) swaps = True while gap > 1 or swaps: gap = max(1, int(gap / 1.25)) # minimum gap is 1 swaps = False for i in range(len(data) - gap): j = i + gap if data[i] > data[j]: data[i], data[j] = data[j], data[i] swaps = True return data 

Sortir cepat :: Sortir cepat

Nah, algoritma pertukaran paling canggih.

1. Bagilah array menjadi dua. Elemen tengah adalah referensi.
2. Kami bergerak dari tepi kiri array ke kanan, sampai kami menemukan elemen yang lebih besar dari yang referensi.
3. Kami bergerak dari tepi kanan array ke kiri hingga kami menemukan elemen yang lebih kecil dari yang referensi.
4. Kami menukar dua elemen yang ditemukan di poin 2 dan 3.
5. Kami terus melakukan item 2-3-4 hingga pertemuan terjadi sebagai akibat dari gerakan timbal balik.
6. Pada titik pertemuan, array dibagi menjadi dua bagian. Untuk setiap bagian, kami menerapkan algoritma pengurutan cepat secara rekursif.

Mengapa ini berhasil? Di sebelah kiri titik pertemuan adalah elemen yang lebih kecil atau sama dengan yang referensi. Di sebelah kanan titik pertemuan adalah elemen yang lebih besar atau sama dengan referensi. Artinya, setiap elemen dari sisi kiri kurang dari atau sama dengan elemen apa pun dari sisi kanan. Oleh karena itu, pada titik pertemuan, array dapat dengan aman dibagi menjadi dua subarrays dan mengurutkan masing-masing subarray dengan cara yang serupa secara rekursif.

 def quick(data): less = [] pivotList = [] more = [] if len(data) <= 1: return data else: pivot = data[0] for i in data: if i < pivot: less.append(i) elif i > pivot: more.append(i) else: pivotList.append(i) less = quick(less) more = quick(more) return less + pivotList + more 

K-sort :: K-sort

Pada Habré, terjemahan dari salah satu artikel diterbitkan, yang melaporkan tentang modifikasi QuickSort, yang mengungguli pengurutan piramida oleh 7 juta elemen. Ngomong-ngomong, ini sendiri merupakan pencapaian yang meragukan, karena penyortiran piramida klasik tidak memecahkan rekor kinerja. Secara khusus, kompleksitas asimptotiknya dalam keadaan apa pun tidak mencapai O (n) (fitur dari algoritma ini).

Tetapi masalahnya berbeda. Menurut pseudo-code penulis (dan jelas salah), umumnya tidak mungkin untuk memahami apa, sebenarnya, ide utama dari algoritma. Secara pribadi, saya mendapat kesan bahwa penulis adalah beberapa penjahat yang bertindak sesuai dengan metode ini:

1. Kami mendeklarasikan penemuan algoritma penyortiran super.
2. Kami memperkuat pernyataan dengan pseudo-code yang tidak berfungsi dan tidak bisa dipahami (seperti, pintar dan sangat jelas, tetapi orang bodoh masih tidak bisa mengerti).
3. Kami menyajikan grafik dan tabel yang seharusnya menunjukkan kecepatan praktis dari algoritma pada data besar. Karena kurangnya kode yang benar-benar berfungsi, masih tidak ada yang dapat memverifikasi atau menyangkal perhitungan statistik ini.
4. Kami menerbitkan omong kosong di Arxiv.org dengan kedok artikel ilmiah.
5. KEUNTUNGAN !!!

Mungkin saya sedang berbicara dengan sia-sia kepada orang-orang dan pada kenyataannya algoritma ini bekerja? Adakah yang bisa menjelaskan cara kerja k-sort?

UPD Tuduhan menyapu saya tentang penulis penipuan ternyata tidak dapat dipertahankan :) Pengguna jetsys menemukan pseudo-code dari algoritma, menulis versi yang berfungsi dalam PHP dan mengirimkannya kepada saya dalam pesan pribadi:

Pengumuman

Itu semua teori, saatnya beralih ke latihan. Artikel selanjutnya adalah pengujian pertukaran sortir pada set data yang berbeda. Kami akan mencari tahu:

• Penyortiran apa yang terburuk - konyol, membosankan, atau membosankan?
• Apakah optimisasi dan modifikasi pada bubble sorting sangat membantu?
• Dalam kondisi apa algoritma lambat dengan cepat dalam kecepatan QuickSort?

Dan ketika kita menemukan jawaban untuk pertanyaan-pertanyaan paling penting ini, kita dapat mulai mempelajari kelas berikutnya - jenis sisipan.

Referensi

Aplikasi-Excel , AlgoLab , yang dengannya Anda dapat selangkah demi selangkah melihat visualisasi dari jenis-jenis ini (dan bukan hanya ini).

Wiki - Silly / Stooge , Lambat , Kerdil / Gnome , Gelembung / Gelembung , Pengocok / Pengocok , Ganjil / Genap , Sisir / Sisir , Cepat / Cepat

Artikel Seri

• Aplikasi Excel AlgoLab.xlsm
• Pertukaran macam
  • Perbandingan Penukaran Exchange
• Urutan Penyisipan
• Sortir berdasarkan pilihan
• Gabungkan Urusan
• Urutkan berdasarkan distribusi
• Sortasi Hibrid