Richard Hamming: Bab 17. Filter Digital - IV

"Tujuan kursus ini adalah untuk mempersiapkan Anda untuk masa depan teknis Anda."

Hai, Habr. Ingat artikel yang luar biasa "Anda dan Pekerjaan Anda" (+219, 2442 bookmark, 393k dibaca)?

Jadi Hamming (ya, ya, memeriksa sendiri dan memperbaiki kode Hamming ) memiliki seluruh buku yang ditulis berdasarkan ceramahnya. Kami menerjemahkannya, karena lelaki itu berbicara bisnis.

Buku ini bukan hanya tentang IT, itu adalah buku tentang gaya berpikir orang yang sangat keren. “Ini bukan hanya muatan pemikiran positif; itu menggambarkan kondisi yang meningkatkan peluang melakukan pekerjaan dengan baik. ”

Kami telah menerjemahkan 24 (dari 30) bab. Dan kami sedang mengerjakan edisi kertas.

Bab 17. Filter Digital - IV

(Terima kasih atas terjemahannya, Andrei Pakhomov, yang menanggapi panggilan saya di "bab sebelumnya".) Siapa yang ingin membantu dengan terjemahan, tata letak, dan penerbitan buku - tulis dalam email pribadi atau magisterludi2016@yandex.ru

Dan sekarang kita beralih ke filter rekursif, yang memiliki bentuk berikut:



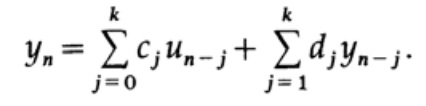
Rumus ini menunjukkan bahwa kami hanya memiliki nilai di satu sisi dari nilai n saat ini. Kami menggunakan nilai-nilai sebelumnya dari sinyal dan nilainya pada waktu saat ini, serta nilai-nilai sebelumnya yang diperoleh pada output filter.
Pendekatan klasik ini adalah hasil dari kenyataan bahwa kita sering memproses sinyal secara real time dan kita tidak memiliki akses ke nilai sinyal di masa depan.

Mengingat dasar-dasarnya, kita akan melihat bahwa jika kita memiliki "nilai masa depan", mungkin peramalan dua arah akan jauh lebih akurat. Kemudian, untuk menghitung yn, kita akan menemukan sebuah sistem yang secara instan akan menyelesaikan persamaan linear - tidak apa-apa di era komputasi murah. Kita akan mengesampingkan pengamatan ini, hari ini kita sering merekam sinyal pada kaset atau media lain, dan kemudian memproses data di laboratorium - dan oleh karena itu kita memiliki nilai masa depan untuk beberapa titik waktu. Misalnya, menggunakan filter digital rekursif dalam pemrosesan gambar akan menjadi bodoh karena tidak menggunakan beberapa informasi yang tersedia dan relevan.

Aspek berikutnya yang perlu Anda perhatikan ketika menggunakan nilai output sebelumnya sebagai input berikutnya adalah adanya umpan balik - dan ini secara otomatis meningkatkan masalah stabilitas. Ini adalah kondisi yang kita harus terus memantau selama desain filter rekursif. Ini membatasi apa yang bisa kita lakukan. Dalam hal ini, stabilitas berarti bahwa efek dari kondisi awal tidak akan mulai berlaku pada hasil akhir.

Ketika bekerja dengan sistem linier, kami melihat bahwa tidak peduli frekuensi apa pun yang kami terapkan pada input filter ketika stasioner, hanya frekuensi ini yang muncul pada output filter, meskipun fase sinyal output dapat digeser relatif terhadap fase sinyal asli. Namun, dalam keadaan transisi, frekuensi lain mungkin muncul yang muncul dari solusi persamaan diferensial yang homogen. Filter rekursif tidak lebih dari solusi persamaan diferensial dengan koefisien konstan untuk un istilah yang membentuk fungsi pemaksaan.

Oleh karena itu, untuk keadaan stasioner (mengabaikan transien), kami menganggap itu



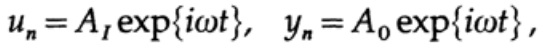
(di mana A dapat berupa bilangan kompleks untuk memperhitungkan pergeseran fasa), dan ini mengarah ke solusi rasio A0 / A1 untuk menemukan fungsi transfer:



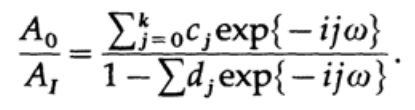
Ekspresi ini adalah fungsi rasional dari variabel kompleks exp {iωt} = z, berbeda dengan filter non-rekursif yang sebelumnya dianggap, di mana karakteristik transfer adalah polinomial dalam z. Bagian teoritis dari representasi fungsi dalam bentuk ekspansi dalam deret Fourier dikembangkan; tetapi sejauh ini tidak ada teori tentang representasi fungsi sebagai hubungan dua seri Fourier (saya pikir tidak ada alasan mengapa teori semacam itu tidak ada). Oleh karena itu, saat ini, metode desain tidak sistematis (yang dilakukan Kaiser untuk desain filter non-rekursif), tetapi lebih merupakan serangkaian trik.

Dengan demikian, kami memiliki filter Butterworth, dua jenis filter Chebyshev (tergantung pada keberadaan riak yang sama pada pita pass dan suppression) dan filter elips (yang dinamakan demikian karena penggunaan fungsi elips), yang memiliki riak yang sama di kedua pita.



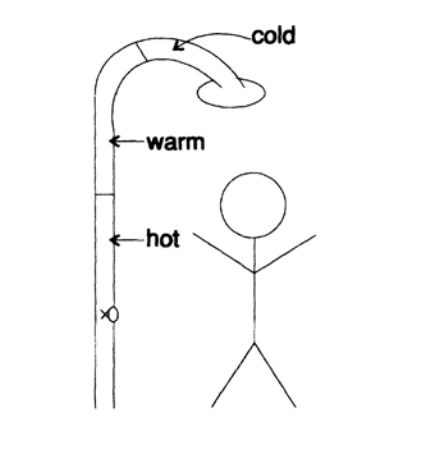Gambar 17.1

Saya hanya akan menyentuh pada topik umpan balik. Untuk memperjelas masalah umpan balik, saya akan bercerita tentang saya kepada Anda. Sekali waktu, saya mengambil bagian dalam serangkaian enam acara televisi setengah jam di komputer dan komputasi. Syuting berlangsung terutama di San Francisco. Saya sering tinggal di sana dan memiliki kebiasaan tinggal di kamar yang sama di hotel yang sama - senang mengetahui kamar secara terperinci ketika sudah larut malam dan Anda lelah atau ketika Anda harus bangun di tengah malam - karena itu keinginan untuk tinggal di kamar yang sama ruangan.

Sangat bagus bahwa tukang ledeng menghubungkan pancuran ke pipa besar (Gambar 17.I). Akibatnya, di pagi hari ketika saya mulai mandi airnya terlalu dingin, saya memutar pegangan keran dengan air hangat lebih banyak, masih terlalu dingin, dan lebih banyak, masih terlalu dingin, dan bahkan lebih, dan akhirnya, ketika air mendapatkan suhu yang tepat Saya tinggal. Tentu saja, air semakin panas dan semakin panas ketika air yang sebelumnya masuk ke pipa keluar, dan saya harus melompat keluar dari kamar mandi dan mencoba lagi untuk menemukan posisi yang cocok untuk pegangan keran air panas. Keterlambatan penyediaan air panas menyebabkan saya tidak nyaman. Terlepas dari pengalaman yang kaya, saya menemukan diri saya dalam situasi klasik ketidakstabilan. Anda dapat melihat situasi ini dari salah satu dari dua sisi: respons saya terlalu kuat (tindakan saya sangat kasar) atau deteksi sinyal terlambat (saya terlalu terburu-buru menyesuaikan keran). Efek jangka panjang yang sama! Saya belum pernah berurusan dengan penundaan yang lama sebelumnya, jadi setiap hari pagi saya dimulai dengan ketidaknyamanan! Dalam contoh ilustratif ini, Anda dapat melihat inti dari ketidakstabilan.

Di sini saya tidak akan mempelajari desain filter rekursif, saya hanya mencatat bahwa selama perjuangan dengan rumus korektif untuk solusi numerik persamaan diferensial biasa, saya secara independen mengembangkan satu teori.

Korektor dalam metode prediktor-korektor memiliki formulir



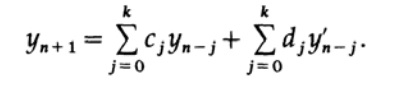
Kita melihat bahwa sekarang koefisien uj dari filter rekursif adalah turunan yn 'dari output filter, yang diambil dari persamaan diferensial. Filter non-rekursif konvensional tidak memiliki loop umpan balik - nilai yn yang dihitung tidak muncul kemudian di sisi kanan ekspresi. Dalam persamaan diferensial, mereka muncul baik dalam loop umpan balik maupun dalam turunannya, sehingga membentuk loop umpan balik lain, biasanya non-linear. Oleh karena itu, stabilitas di bidang penyelesaian persamaan diferensial adalah topik yang lebih rumit daripada di bidang filter rekursif.

Filter rekursif seperti itu sering disebut "filter dengan respons impuls tak terbatas" (filter IIR), karena gangguan tunggal akan bergema melalui loop umpan balik, yang akan membusuk secara eksponensial, dan hanya jika filter stabil. Saya tidak akan menjadi diri saya sendiri jika saya tidak bertanya-tanya apakah semua filter rekursif harus memiliki properti ini. Segera saya menemukan contoh sebaliknya. Sebenarnya, ini bukan jenis filter yang biasanya Anda desain, tetapi contoh ini menunjukkan bahwa pernyataan ini dangkal. Jika Anda bertanya pada diri sendiri apakah semua yang Anda katakan itu benar, maka Anda akan terkejut betapa banyak hal yang ternyata salah, bahkan di area yang dirancang dengan baik!

Dalam Bab 26, saya akan membahas masalah bekerja dengan para ahli. Anda sekarang akan melihat contoh dari apa yang terjadi terlalu sering. Para ahli diberitahu sesuatu di kelas ketika mereka masih siswa, dan mereka tidak mengajukan pertanyaan, mereka hanya menganggapnya sebagai fakta. Dan mereka terus-menerus mereproduksi fakta yang diterima ini bahkan tanpa berusaha memeriksa apakah itu benar atau tidak, terutama dalam kaitannya dengan masalah yang mereka coba selesaikan pada saat ini.

Izinkan saya menceritakan kisah lain kepada Anda sekarang. Seorang wanita dari departemen matematika di Lab Laboratorium Bella sedang menari tarian persegi dengan salah satu fisikawan di pesta akhir pekan, dan pada Senin pagi, di lorong, dia mengatakan kepada saya masalah yang dia alami. Dia mengukur jumlah pulsa dalam percobaan radioaktif di masing-masing, seingat saya, 256 tingkat energi. Ini disebut spektrum proses. Masalahnya adalah mendapatkan turunan dari data.

Jadi, Anda tahu bahwa (a) jumlah pulsa pada tingkat energi tertentu akan membentuk kurva dengan diskontinuitas, dan (b) membedakannya untuk mendapatkan koefisien sudut lokal bukanlah tugas yang mudah. Semakin saya memikirkan catatan acaknya, semakin saya merasa bahwa dia membutuhkan penolong yang baik - yaitu, saya! Saya menemukannya di direktori telepon Bell Laboratories dan menjelaskan kepadanya minat saya dan bagaimana saya mendapatkannya. Dia segera ingin datang ke kantor saya, tetapi saya keras kepala, dan bersikeras untuk bertemu di laboratoriumnya. Dia mencoba menawarkan kantornya, tetapi saya masih bersikeras di laboratoriumnya. Mengapa Untuk mengevaluasi kemampuannya dan memutuskan apakah masalahnya sepadan dengan waktu dan upaya saya, karena itu akan sulit untuk dipecahkan. Dia lulus ujian dengan gemilang oleh laboratorium - menjadi jelas bahwa dia adalah seorang eksperimen yang sangat kompeten.

Dia hampir pada batas apa yang bisa dia lakukan - data dikumpulkan selama seminggu, dan sumber radiasi disembunyikan oleh banyak layar. Sepertinya Anda tidak dapat melakukan hal lain untuk mengumpulkan data yang lebih akurat. Selain itu, saya segera menjadi yakin, meskipun saya tahu sedikit detail, bahwa eksperimennya penting untuk fisika dan juga untuk Bell Laboratories. Jadi, saya mengambil tugas ini. Moral: sampai batas tertentu, Anda dapat memilih dan mengerjakan tugas-tugas yang menurut Anda penting.

Jelas, ini adalah masalah perataan, dan Kaiser, pada kenyataannya, baru saja melatih saya, jadi apa yang bisa lebih baik daripada membawa eksperimen ke Kaiser dan meminta Kaiser merancang filter pembeda yang cocok? Masalahnya segera dimulai. Kaiser selalu menganggap sinyal sebagai fungsi waktu, dan area di bawah kurva sebagai energi, dan dalam hal ini energi adalah variabel independen! Pada titik ini, masalah dengan Kaiser diulang sampai saya langsung mengatakan kepadanya: "Yah, energinya adalah waktu, dan pengukurannya, impuls, tegangan ini." Baru setelah itu Kaiser mampu menyelesaikan masalah.

Kutukan para ahli terletak pada pemahaman mereka yang terbatas tentang apa yang bisa mereka lakukan. Saya mengatakan kepada Anda bahwa Kaiser adalah orang yang sangat cakap, tetapi pengalamannya, seperti yang sering terjadi dengan para ahli, membatasi visinya. Bisakah Anda, pada gilirannya, melakukan lebih baik? Saya harap cerita ini membantu Anda menghindari jebakan ini.

Seperti yang saya perhatikan sebelumnya, biasanya spektrum sinyal berguna berada di bagian bawah pita Nyquist, dan spektrum kebisingan didistribusikan ke seluruh pita Nyquist, jadi kami harus menemukan frekuensi cutoff antara sinyal bermanfaat dari fisikawan dan kebisingan putih datar. Bagaimana cara menemukannya? Pada awalnya, saya mencoba model teoritis percobaan dari kepala fisikawan yang ada di kepalanya - banyak garis spektral sempit dalam bentuk fungsi Gaussian di atas fungsi Gaussian yang luas (saya ragu bahwa ini adalah distribusi Cauchy, tetapi tidak membantah, karena perbedaannya akan sangat kecil, mengingat sifat data yang kami miliki). Jadi, kami mensimulasikan distribusi ini, dan dia menyiapkan sejumlah data sintetik yang sesuai dengan model ini. Analisis spektral cepat sinyal melalui transformasi Fourier cepat menunjukkan bahwa sinyal terletak di 1/20 lebih rendah dari band Nyquist. Selanjutnya, kami memproses data eksperimentalnya dengan cara yang sama dan mendapatkan lokasi frekuensi cutoff yang sama! Benar-benar keberuntungan! (Mungkin keberuntungan harus dikaitkan dengan keterampilan eksperimen). Sekali waktu, teori dan praktik datang bersama! Ternyata kami dapat menyaring 95% dari kebisingan. Akhirnya, Kaiser menulis sebuah program untuknya yang mensintesis sebuah filter untuk frekuensi cutoff yang diberikan, yang ditetapkan oleh eksperimen.

Program (1) menghitung filter pembeda yang sesuai, (2) menulis program untuk menghitung output yang dihaluskan, dan kemudian (3) memproses data dengan filter ini tanpa intervensi dari fisikawan.

Kemudian, saya menangkap seorang fisikawan dengan menyesuaikan frekuensi cutoff untuk bagian-bagian berbeda dari data tingkat energi yang diperoleh dalam satu rangkaian pengukuran dan dipaksa untuk mengingatkannya bahwa ada "derajat kebebasan" tertentu dan apa yang dia lakukan bukanlah pemrosesan data yang jujur. Menjadi jauh lebih bermasalah ketika segalanya berjalan baik, untuk membujuknya untuk mendapatkan yang terbaik dari datanya (yang sangat mahal untuk diperoleh) - ia harus bekerja dengan akar kuadrat dari impulsnya, karena mereka memiliki varian yang sama. Akhirnya, dia mengerti ini dan melakukannya. Dia dan Kaiser menulis karya klasik di bidang ini yang membuka pintu untuk hal-hal baru yang bisa dilakukan.

Kontribusi saya Terutama, pertama mengidentifikasi masalah, kemudian menyatukan orang yang tepat, kemudian menonton Kaiser untuk berhadapan dengannya dengan fakta bahwa penyaringan diperlukan tidak hanya untuk sinyal sebagai fungsi waktu, dan akhirnya mengingatkan mereka tentang apa yang mereka ketahui dari statistik (atau seharusnya memiliki untuk tahu, tetapi mungkin mereka tidak tahu).

Atas dasar milik saya, bagi saya tampaknya kebutuhan akan peran seperti itu meningkat ketika orang-orang menjadi semakin banyak ahli dalam bidang pengetahuan yang semakin sempit. Seseorang perlu menjaga wawasan yang luas dan memastikan bahwa segala sesuatunya dilakukan dengan jujur. Saya pikir saya datang ke peran ini setelah pendidikan yang sangat panjang di bawah kepemimpinan John Tukey di samping fondasi yang baik dalam bentuk alat universal Ilmu yang disebut Matematika. Saya akan berbicara tentang sifat Matematika di Bab 23 .

Sebagian besar pemrosesan sinyal berasal dari sinyal dari waktu ke waktu. Pada saat yang sama, sebagian besar filter digital dirancang untuk studi kecil yang sangat terspesialisasi yang tidak selalu dikaitkan dengan sinyal dari waktu ke waktu. Di sini saya akan meminta Anda untuk berhati-hati di masa depan. Misalkan Anda menjalankan bisnis di bagian paling atas dan tertarik pada data yang menunjukkan biaya tenaga kerja sebelumnya untuk peralatan. Ini akan menjadi data yang berisik, tetapi Anda masih ingin memahami, dalam arti biasa, apa yang terjadi dalam organisasi - proses jangka panjang apa yang terjadi - proses yang sangat lambat sehingga orang akan memahaminya ketika mereka sudah terjadi, tetapi tetap mengerti menangkap yang secara fundamental penting jika Anda ingin menjadi manajer yang baik. Anda akan membutuhkan filter digital untuk memuluskan data dan melihat petunjuk tren, jika ada. Anda tidak ingin menemukan tren yang tidak ada, tetapi jika ada, maka Anda benar-benar ingin tahu apa itu sebelumnya untuk memprediksi seperti apa kemungkinannya dalam waktu dekat. Bahkan, Anda akan ingin melihat perubahan pada kemiringan tren, jika data memungkinkan Anda untuk melihatnya. Beberapa sinyal, seperti daya tembak sehubungan dengan perpindahan kapal, tidak terikat dengan waktu, tetapi mereka dapat memberi tahu Anda banyak tentang kondisi armada saat ini. Tentu saja, Anda dapat mempelajari hubungan ini sebagai fungsi waktu.

Di puncak karir Anda, Anda akan dapat menggunakan berbagai filter digital tingkat rendah untuk sinyal sebagai fungsi waktu, dan tidak hanya untuk mengelola berbagai hal dengan lebih baik. Oleh karena itu, saya berpendapat bahwa Anda mungkin mensintesis lebih banyak filter digital untuk hal-hal yang tidak standar daripada untuk memperkecil data radar dan aplikasi klasik serupa. Biasanya dalam aplikasi pengetahuan baru Anda bisa mendapatkan hasil maksimal.

Izinkan saya mengungkapkan beberapa kekhawatiran terkait penggunaan alat cerdas yang tidak benar, lebih detail saya akan berbicara tentang topik yang dekat dengan statistik pada Bab 27 . Analisis ekspansi Fourier mengasumsikan linearitas dari model yang mendasarinya. Anda dapat menggunakannya untuk kasus-kasus yang sedikit non-linear, tetapi lebih sering daripada tidak, analisis yang dilakukan oleh ekspansi Fourier gagal, karena fenomena yang diselidiki terlalu non-linear. Saya melihat bagaimana jutaan dolar terbuang ketika sangat jelas bagi orang luar bahwa non-linearitas akan mendistorsi seluruh analisis linear yang dilakukan dengan pendekatan oleh seri Fourier. Ketika mereka menunjukkan ini, jawaban mereka adalah bahwa mereka tidak tahu pendekatan apa yang bisa diambil, sehingga mereka terus melakukan hal yang salah! Dan saya tidak melebih-lebihkan di sini.



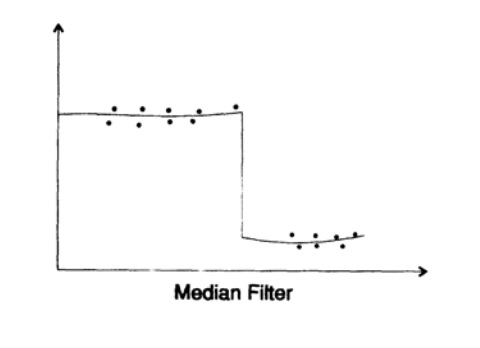Gambar 17.2

Bagaimana dengan filter non-linear? Kemungkinan di sini tidak terbatas dan tergantung, tentu saja, pada masalah yang Anda hadapi. Saya hanya akan berurusan dengan salah satunya, filter median.Anda mempertimbangkan output filter median untuk dataset tertentu. Mari kita lihat cara kerjanya dalam praktik. Pertama-tama, kami mencatat bahwa filter ini berupaya memuluskan kebisingan lokal, tetapi bagaimana filter akan berperilaku pada titik istirahat (Gbr. 17.2)?

Dengan jumlah anggota yang ganjil dalam filter median, Anda akan melihat bahwa output filter tetap pada level atas hingga lebih dari setengah titik pada input filter berada pada level yang lebih rendah, setelah itu output filter "melompat" ke bawah. Dia akan mengikuti istirahat dengan cukup baik dan tidak akan mencoba untuk menghaluskannya sepenuhnya! Dalam beberapa kasus, ini adalah jenis filter yang cocok untuk Anda - kebisingan lokal dihaluskan, sementara perubahan mendadak dalam kondisi sistem yang sedang dipelajari tidak akan hilang.

Saya ulangi bahwa analisis oleh seri Fourier adalah linier, sementara ada sejumlah besar filter non-linear, tetapi teorinya tidak dikembangkan dengan baik untuk apa pun selain filter median. Filter Kalman adalah contoh lain dari penggunaan filter non-linier sebagian, bagian non-linear adalah "penyesuaian" independen filter untuk sinyal.

Akhirnya, inilah pengamatan mendasar lain yang saya lakukan ketika mempelajari filter digital. Suatu hari, ketika mempelajari sebuah buku tentang Fourier integral, saya menemukan teorema yang mengklaim bahwa variasi fungsi dikalikan dengan variasi transformasinya harus lebih besar daripada konstanta tertentu. Saya bertanya pada diri sendiri: "Apa itu tapi prinsip terkenal ketidakpastian Mekanika Quantum"? Ya, setiap teori linier harus memiliki prinsip ketidakpastian yang menghubungkan variabel konjugat. Segera setelah Anda mengadopsi pendekatan linier, dan CM menyatakan aditivitas absolut dari status eigen, Anda harus menemukan prinsip ketidakpastian. Invarian linear waktu secara otomatis mengarah ke fungsi eigen e ^ iω (t). Mereka segera mengarah ke seri Fourier, dan mereka, pada gilirannya, memiliki prinsip ketidakpastian.Seolah-olah Anda mengenakan kacamata berwarna biru. Apa pun yang Anda lihat, itu akan memiliki warna kebiruan!

Oleh karena itu, Anda tidak benar-benar yakin apakah ada prinsip ketidakpastian CM yang terkenal atau tidak; mungkin ini hanya efek dari linearitas tersirat dari sistem.

Hanya sedikit orang yang ingin percaya bahwa apa yang kita lihat tergantung pada sisi mana kita mendekati masalah! Sangat sering kita melihat apa yang ingin kita lihat, dan itulah sebabnya Anda harus menggunakan pendekatan ilmiah di mana-mana, meragukan keyakinan Anda sendiri.
Untuk menunjukkan ini dengan jelas, saya akan mengulangi kisah Eddington tentang nelayan. Mereka memancing di jaring, dan ketika mereka memeriksa ukuran ikan yang ditangkap di jaring, mereka memutuskan bahwa ada ukuran minimum ikan di laut.

Kesimpulannya, jika Anda tidak meragukan aturan yang diadopsi, sekarang dan kemudian, maka kemungkinan besar Anda tidak akan menjadi pemimpin di bidang apa pun, di sisi lain, jika Anda meragukan segalanya, Anda akan lumpuh dan tidak akan melakukan apa pun. . Kapan ragu, kapan harus belajar dasar-dasarnya, kapan harus berpikir untuk dirimu sendiri, dan kapan harus melanjutkan dan mengambil apa adanya, ini masalah gaya berpikir, dan aku tidak bisa memberikan formula sederhana untuk menyelesaikan masalah ini. Anda harus belajar dari pengalaman Anda sendiri. Keuntungan besar biasanya datang setelah perubahan signifikan dalam asumsi mendasar yang menjadi dasar daerah tersebut. Keadaan pengetahuan kita menentukan keseimbangan antara berbagai aspek penelitian. Tampaknya ketika Anda masih muda, intuisi dan wawasan memiliki lebih banyak waktu untuk membayar, tetapi ketika Anda sudah tua,sedikit waktu yang tersisa untuk ini dan mungkin harus berkonsentrasi pada apa yang sudah ada di ujung jari Anda.

Dilanjutkan ...

Siapa yang ingin membantu dengan terjemahan, tata letak, dan penerbitan buku - tulis dalam email pribadi atau magisterludi2016@yandex.ru

Ngomong-ngomong, kami juga telah meluncurkan terjemahan buku keren lainnya - “Mesin Impian: Sejarah Revolusi Komputer” )