Pemetaan normal

Semua adegan yang kami gunakan terbuat dari poligon, yang pada gilirannya terdiri dari ratusan, ribuan segitiga yang benar-benar datar. Kami telah berhasil sedikit meningkatkan realisme adegan karena detail tambahan yang menyediakan aplikasi tekstur dua dimensi pada segitiga datar ini. Tekstur membantu menyembunyikan fakta bahwa semua objek dalam adegan hanyalah kumpulan banyak segitiga kecil. Teknik yang hebat, tetapi kemungkinannya tidak terbatas: ketika mendekati permukaan apa pun, semua menjadi jelas bahwa itu terdiri dari permukaan datar. Sebagian besar benda nyata tidak sepenuhnya rata dan menunjukkan banyak detail lega.


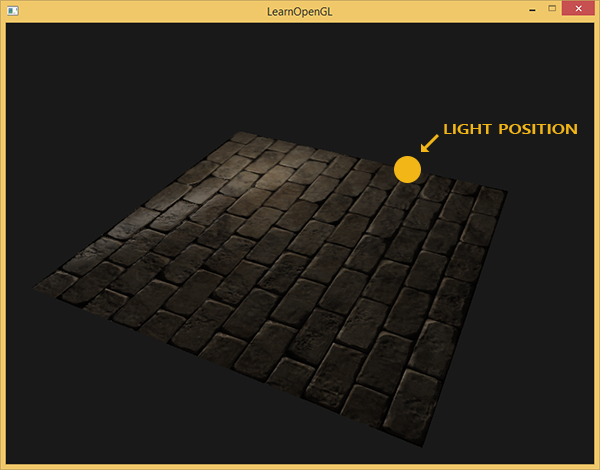
Misalnya, ambil batu bata. Permukaannya sangat kasar dan, jelas, tidak diwakili oleh pesawat: di atasnya ada ceruk dengan semen dan banyak detail kecil seperti lubang dan retakan. Jika kita menganalisis sebuah adegan dengan meniru batu bata di hadapan pencahayaan, maka ilusi relief permukaan sangat mudah dihancurkan. Berikut ini adalah contoh pemandangan yang mengandung bidang dengan tekstur batu dan satu titik sumber cahaya:


Seperti yang Anda lihat, pencahayaan sama sekali tidak memperhitungkan rincian relief yang diasumsikan untuk permukaan ini: semua retakan kecil dan rongga dengan semen juga tidak dapat dibedakan dari bagian permukaan lainnya. Orang dapat menggunakan peta gloss specular untuk membatasi penerangan detail tertentu yang ada di ceruk permukaan. Tapi ini lebih mirip hack kotor daripada solusi yang berfungsi. Yang kita butuhkan adalah cara untuk memberikan persamaan pencahayaan dengan data pada permukaan microrelief.
Dalam konteks persamaan pencahayaan yang kita kenal, pertimbangkan pertanyaan ini: dalam kondisi apa permukaan akan diterangi sebagai rata sempurna? Jawabannya terkait dengan normal ke permukaan. Dari sudut pandang algoritma pencahayaan, informasi tentang bentuk permukaan ditransmisikan hanya melalui vektor normal. Karena vektor normal adalah konstan di mana-mana pada permukaan yang ditunjukkan di atas, iluminasi juga keluar seragam, sesuai dengan bidang. Tetapi bagaimana jika kita beralih ke algoritma pencahayaan bukan satu-satunya konstanta normal untuk semua fragmen milik objek, tetapi unik unik untuk setiap fragmen? Dengan demikian, vektor normal akan sedikit berubah berdasarkan topografi permukaan, yang akan menciptakan ilusi kompleksitas permukaan yang lebih meyakinkan:


Melalui penggunaan normals yang berbeda secara terpisah, algoritma pencahayaan akan menganggap permukaan terdiri dari banyak bidang mikroskopis yang tegak lurus dengan vektor normalnya. Sebagai hasilnya, ini akan secara signifikan menambah tekstur pada objek. Teknik menerapkan normals unik untuk sebuah fragmen, dan tidak untuk seluruh permukaan - ini adalah Pemetaan Normal atau Pemetaan Bump . Seperti yang diterapkan pada adegan yang sudah akrab:


Anda dapat melihat peningkatan kompleksitas visual yang mengesankan karena biaya kinerja yang sangat sederhana. Karena kita semua perubahan dalam model pencahayaan hanya dalam penyediaan normal yang unik di setiap fragmen, maka tidak ada rumus perhitungan yang diubah. Hanya pada input, bukan interpolasi normal, normal untuk fragmen saat ini muncul ke permukaan. Semua persamaan pencahayaan yang sama melakukan sisa pekerjaan untuk menciptakan ilusi kelegaan.

Pemetaan normal

Jadi, ternyata, kita perlu menyediakan algoritma pencahayaan dengan normals yang unik untuk setiap fragmen. Kami akan menggunakan metode yang sudah akrab dalam tekstur refleksi difus dan specular dan menggunakan tekstur 2D biasa untuk menyimpan data normal di setiap titik di permukaan. Jangan kaget, tekstur juga bagus untuk menyimpan vektor normal. Maka kita hanya harus memilih dari tekstur, mengembalikan vektor normal dan melakukan perhitungan pencahayaan.

Sekilas, mungkin tidak begitu jelas bagaimana cara menyimpan data vektor dalam tekstur biasa, yang biasanya digunakan untuk menyimpan informasi warna. Tapi pikirkan sebentar: triad warna RGB pada dasarnya adalah vektor tiga dimensi. Dengan cara yang sama, Anda dapat menyimpan komponen-komponen dari vektor normal XYZ dalam komponen warna yang sesuai. Nilai-nilai komponen vektor normal terletak pada interval [-1, 1] dan karenanya memerlukan konversi tambahan ke interval [0, 1]:

vec3 rgb_normal = normal * 0.5 + 0.5; //   [-1,1]  [0,1] 

Pengurangan seperti itu dari vektor normal ke ruang komponen warna RGB akan memungkinkan kita untuk menyimpan vektor normal dalam tekstur, diperoleh atas dasar relief nyata dari objek yang dimodelkan dan unik untuk setiap fragmen. Contoh tekstur seperti itu - peta normal - untuk tembok yang sama:


Sangat menarik untuk mencatat warna biru dari peta normal ini (hampir semua peta normal memiliki warna yang sama). Ini terjadi karena semua normalnya berorientasi kira-kira di sepanjang sumbu oZ, yang diwakili oleh triple koordinat (0, 0, 1), yaitu dalam bentuk triad warna - biru murni. Perubahan kecil dalam rona adalah konsekuensi dari penyimpangan normals dari oZ semi-sumbu positif di beberapa daerah, yang sesuai dengan medan yang tidak rata. Jadi, Anda dapat melihat bahwa di tepi atas setiap bata, teksturnya mengambil rona hijau. Dan ini logis: pada permukaan atas bata, normals harus lebih berorientasi pada sumbu O (0, 1, 0), yang sesuai dengan hijau.

Untuk adegan pengujian, ambil bidang yang berorientasi ke arah semi-sumbu positif OZ dan gunakan peta difus berikut dan peta normal untuknya.

Harap dicatat bahwa peta normal pada tautan dan pada gambar di atas berbeda. Dalam artikel tersebut, penulis dengan santai menyebutkan alasan perbedaan, membatasi dirinya pada saran untuk mengkonversi peta normal sedemikian rupa sehingga komponen hijau menunjukkan "turun" daripada "naik" dalam sistem lokal ke bidang tekstur.
Jika Anda melihat lebih detail, maka dua faktor berinteraksi di sini:

• Perbedaannya adalah bagaimana texels dialamatkan dalam memori klien dan dalam memori tekstur OpenGL
• Kehadiran dua notasi untuk peta normal. Secara konvensional, dua kubu: DirectX-style dan OpenGL-style

Mengenai notasi peta normal, secara historis familiar adalah dua kubu: DirectX dan OpenGL.

Tampaknya, mereka tidak kompatibel. Dan dengan sedikit pemikiran, Anda dapat memahami bahwa DirectX menganggap ruang singgung menjadi tangan kiri dan OpenGL sebagai tangan kanan. Menggeser peta normal X aplikasi kita tanpa perubahan apa pun akan menghasilkan pencahayaan yang salah, dan tidak selalu segera jelas bahwa itu salah. Terutama, tonjolan dalam format OpenGL menjadi lekukan untuk DirectX dan sebaliknya.
Adapun pengalamatan: memuat data dari file tekstur ke dalam memori, kami menganggap bahwa texel pertama adalah texel kiri atas gambar. Untuk merepresentasikan data tekstur dalam memori aplikasi, ini umumnya benar. Tetapi OpenGL menggunakan sistem koordinat tekstur yang berbeda: untuk itu, texel pertama adalah kiri bawah. Untuk tekstur yang benar, gambar biasanya diputar sepanjang sumbu Y dalam kode satu atau lain file loader gambar. Untuk Stb_image yang digunakan dalam pelajaran, Anda perlu menambahkan kotak centang

 stbi_set_flip_vertically_on_load(1); 

Yang lucu adalah bahwa dua opsi ditampilkan dengan benar dalam hal pencahayaan: peta normal dalam notasi OpenGL dengan pantulan Y dihidupkan atau peta normal dalam notasi DirectX dengan pantulan Y dimatikan. Pencahayaan dalam kedua kasus bekerja dengan benar, perbedaannya hanya akan tetap dalam kebalikan dari tekstur sepanjang sumbu. Y.

Catatan trans.

Jadi, muat kedua tekstur, ikat ke blok tekstur dan render bidang yang disiapkan, dengan mempertimbangkan modifikasi berikut dari kode shader fragmen:

 uniform sampler2D normalMap; void main() { //         [0,1] normal = texture(normalMap, fs_in.TexCoords).rgb; //      [-1,1] normal = normalize(normal * 2.0 - 1.0); [...] //  ... } 

Di sini kami menerapkan transformasi terbalik dari ruang nilai RGB ke vektor normal penuh dan kemudian menggunakannya dalam model pencahayaan Blinn-Fong yang terkenal.

Sekarang, jika Anda perlahan-lahan mengubah posisi sumber cahaya dalam adegan, Anda dapat merasakan ilusi relief permukaan yang disediakan oleh peta normal:


Namun masih ada satu masalah yang secara drastis mempersempit kisaran kemungkinan penggunaan peta normal. Seperti yang telah dicatat, warna biru pada peta normal mengisyaratkan bahwa semua vektor pada tekstur rata-rata berorientasi sepanjang sumbu positif oZ. Dalam adegan kami, ini tidak menimbulkan masalah, karena normal ke permukaan pesawat juga selaras dengan oZ. Namun, apa yang terjadi jika kita mengubah posisi pesawat di tempat kejadian sehingga normal untuk itu sejajar dengan sumbu positif oY?


Pencahayaan ternyata sepenuhnya salah! Dan alasannya sederhana: sampel normals dari peta masih mengembalikan vektor yang berorientasi sepanjang setengah-sumbu positif OZ, meskipun dalam kasus ini mereka harus berorientasi ke arah setengah-sumbu positif pada permukaan normal. Pada saat yang sama, perhitungan pencahayaan seolah-olah normals ke permukaan terletak seolah-olah pesawat masih berorientasi pada oZ semi-sumbu positif, yang memberikan hasil yang salah. Gambar di bawah ini lebih jelas menunjukkan orientasi normal dibaca dari peta relatif ke permukaan:


Dapat dilihat bahwa normalnya umumnya disejajarkan sepanjang positif setengah sumbu oZ, meskipun mereka seharusnya telah disejajarkan sepanjang normal ke permukaan yang diarahkan sepanjang positif setengah sumbu oY.
Solusi yang mungkin adalah mengatur peta normal yang terpisah untuk setiap orientasi permukaan yang sedang dipertimbangkan. Untuk kubus, enam peta normal akan dibutuhkan, tetapi untuk model yang lebih kompleks, jumlah orientasi yang mungkin mungkin terlalu tinggi dan tidak cocok untuk implementasi.

Ada lagi, pendekatan matematis yang lebih rumit, yang menawarkan untuk menghitung pencahayaan dalam sistem koordinat yang berbeda: sedemikian rupa sehingga vektor normal di dalamnya selalu kira-kira bertepatan dengan oZ setengah-sumbu positif. Vektor lain yang diperlukan untuk perhitungan pencahayaan kemudian dikonversi ke sistem koordinat ini. Metode ini memungkinkan untuk menggunakan satu peta normal untuk setiap orientasi objek. Dan sistem koordinat khusus ini disebut ruang singgung atau ruang singgung .

Ruang singgung

Perlu dicatat bahwa vektor normal di peta normal diekspresikan secara langsung dalam ruang singgung, mis. dalam sistem koordinat sedemikian rupa sehingga normal selalu diarahkan kira-kira ke arah oZ semi-sumbu positif. Ruang singgung didefinisikan sebagai sistem koordinat lokal ke bidang segitiga, dan setiap vektor normal didefinisikan dalam sistem koordinat ini. Anda dapat membayangkan sistem ini sebagai sistem koordinat lokal untuk peta normal: semua vektor di dalamnya diarahkan langsung ke oZ semi-sumbu positif, terlepas dari orientasi akhir permukaan. Dengan menggunakan matriks transformasi yang disiapkan secara khusus, dimungkinkan untuk mengubah vektor normal dari sistem koordinat tangen lokal ini ke dunia atau melihat koordinat, mengarahkannya sesuai dengan posisi akhir dari permukaan bertekstur.
Perhatikan contoh sebelumnya dengan penggunaan pemetaan normal yang salah, di mana bidangnya berorientasi sepanjang sumbu positif oY. Karena peta normals didefinisikan dalam ruang tangen, salah satu opsi penyesuaian adalah untuk menghitung matriks transisi normals dari ruang tangen ke sedemikian rupa sehingga mereka akan berorientasi normal ke permukaan. Ini akan menyebabkan normals menjadi sejajar sepanjang sumbu positif oY. Sifat luar biasa dari ruang singgung adalah fakta bahwa dengan menghitung matriks seperti itu kita dapat mengubah orientasi normals ke permukaan apa pun dan orientasinya.

Matriks semacam itu disingkat TBN , yang merupakan singkatan untuk nama rangkap tiga vektor Tangent , Bitangent dan Normal . Kita perlu menemukan ketiga vektor ini untuk membentuk matriks dasar perubahan ini. Matriks seperti itu membuat transisi vektor dari ruang singgung ke yang lain dan untuk pembentukannya diperlukan tiga vektor yang saling tegak lurus, yang orientasinya sesuai dengan orientasi bidang peta normal. Ini adalah vektor arah ke atas, ke kanan dan ke depan, seperangkat yang kita kenal dari pelajaran di kamera virtual .
Dengan vektor atas, semuanya menjadi jelas segera - ini adalah vektor normal kita. Vektor kanan dan maju masing-masing disebut tangen dan bitangent . Gambar berikut memberikan gambaran tentang posisi relatif mereka di pesawat:


Perhitungan tangen dan bi-tangen tidak begitu jelas seperti perhitungan vektor normal. Pada gambar, Anda dapat melihat bahwa arah garis singgung dan peta garis singgung normal disejajarkan dengan sumbu yang menentukan koordinat tekstur permukaan. Fakta ini adalah dasar untuk menghitung dua vektor ini, yang akan membutuhkan keterampilan matematika. Lihat gambar:


Perubahan koordinat tekstur di sepanjang tepi segitiga $$$E_2$ ditunjuk sebagai $$$\ Delta U_2$ dan $$$\ Delta V_2$ dinyatakan dalam arah yang sama dengan vektor singgung $$$T$ dan bi-tangent $$$B$ . Berdasarkan fakta ini, Anda dapat mengekspresikan tepi segitiga $$$E_1$ dan $$$E_2$ dalam bentuk kombinasi linear vektor tangen dan bi-tangen:

$$

$$E_1 = \ Delta U_1T + \ Delta V_1B$$

$$

$$E_2 = \ Delta U_2T + \ Delta V_2B$$

Mengubah menjadi catatan bitwise yang kami dapatkan:

$$

$$(E_ {1x}, E_ {1y}, E_ {1z}) = \ Delta U_1 (T_x, T_y, T_z) + \ Delta V_1 (B_x, B_y, B_z)$$

$$

$$(E_ {2x}, E_ {2y}, E_ {2z}) = \ Delta U_2 (T_x, T_y, T_z) + \ Delta V_2 (B_x, B_y, B_z)$$

$$$E$ dihitung sebagai vektor perbedaan dua vektor, dan $$$\ Delta U$ dan $$$\ Delta V$ sebagai perbedaan dalam koordinat tekstur. Masih menemukan dua yang tidak diketahui dalam dua persamaan: garis singgung $$$T$ dan bias $$$B$ . Jika Anda mengingat pelajaran aljabar, Anda tahu bahwa kondisi seperti itu memungkinkan untuk menyelesaikan sistem $$$T$ dan untuk $$$B$ .
Bentuk persamaan terakhir yang diberikan memungkinkan kita untuk menulis ulang dalam bentuk perkalian matriks:

$$

$$\ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Cobalah untuk melakukan penggandaan matriks dalam pikiran Anda untuk memastikan catatan itu benar. Menulis sistem dalam bentuk matriks membuatnya lebih mudah untuk memahami pendekatan untuk menemukan $$$T$ dan $$$B$ . Lipat gandakan kedua sisi persamaan dengan kebalikan dari $$$\ Delta U \ Delta V$ :

$$

$$\ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} ^ {- 1} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z } \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Kami mendapat keputusan $$$T$ dan $$$B$ , yang, bagaimanapun, membutuhkan perhitungan matriks terbalik dari perubahan dalam koordinat tekstur. Kami tidak akan membahas perincian perhitungan matriks invers - ekspresi untuk matriks invers terlihat seperti produk dari jumlah invers ke penentu matriks asli dan matriks adjoint:

$$

$$\ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix} = \ frac {1} {\ Delta U_1 \ Delta V_2 - \ Delta U_2 \ Delta V_1} \ begin {bmatrix} \ Delta V_2 & - \ Delta V_1 \\ - \ Delta U_2 & \ Delta U_1 \ end {bmatrix} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ { 2t} & E_ {2z} \ end {bmatrix}$$

Ekspresi ini adalah rumus untuk menghitung vektor garis singgung $$$T$ dan bi-tangent $$$B$ berdasarkan pada koordinat muka segitiga dan koordinat tekstur yang sesuai.
Jangan khawatir jika esensi dari perhitungan matematis di atas luput dari Anda. Jika Anda memahami bahwa kami mendapatkan garis singgung dan garis singgung bias berdasarkan koordinat titik segitiga dan koordinat teksturnya (karena koordinat tekstur juga termasuk dalam ruang garis singgung) - ini sudah setengah pertempuran.

Perhitungan garis singgung dan bitangen

Dalam contoh pelajaran ini, kami mengambil pesawat sederhana yang memandang ke arah positif setengah sumbu oZ. Sekarang kami akan mencoba menerapkan pemetaan normal menggunakan ruang singgung agar dapat mengorientasikan pesawat dalam contoh sesuai keinginan tanpa merusak efek pemetaan normal. Dengan menggunakan perhitungan di atas, kami secara manual menemukan garis singgung dan dua garis singgung ke permukaan yang sedang dipertimbangkan.
Kami berasumsi bahwa bidang terdiri dari simpul berikut dengan koordinat tekstur (dua segitiga diberikan oleh vektor 1, 2, 3 dan 1, 3, 4):

 //   glm::vec3 pos1(-1.0, 1.0, 0.0); glm::vec3 pos2(-1.0, -1.0, 0.0); glm::vec3 pos3( 1.0, -1.0, 0.0); glm::vec3 pos4( 1.0, 1.0, 0.0); //   glm::vec2 uv1(0.0, 1.0); glm::vec2 uv2(0.0, 0.0); glm::vec2 uv3(1.0, 0.0); glm::vec2 uv4(1.0, 1.0); //   glm::vec3 nm(0.0, 0.0, 1.0); 

Pertama, kami menghitung vektor yang menggambarkan wajah segitiga, serta delta dari koordinat tekstur:

 glm::vec3 edge1 = pos2 - pos1; glm::vec3 edge2 = pos3 - pos1; glm::vec2 deltaUV1 = uv2 - uv1; glm::vec2 deltaUV2 = uv3 - uv1; 

Setelah memiliki data awal yang diperlukan, kita dapat mulai menghitung garis singgung dan bi-tangen langsung dengan rumus dari bagian sebelumnya:

 float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y); tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x); tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y); tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z); tangent1 = glm::normalize(tangent1); bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x); bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y); bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z); bitangent1 = glm::normalize(bitangent1); [...] //         

Pertama, kita mengambil komponen fraksional dari ekspresi akhir dalam variabel terpisah f . Kemudian, untuk setiap komponen vektor, kami melakukan bagian yang sesuai dari perkalian matriks dan dikalikan dengan f . Membandingkan kode ini dengan rumus perhitungan akhir, Anda dapat melihat bahwa ini adalah pengaturan literalnya. Jangan lupa untuk menormalkan pada akhirnya, sehingga vektor yang ditemukan adalah satuan.

Karena segitiga adalah angka rata, itu cukup untuk menghitung garis singgung dan bi-tangen sekali per segitiga - mereka akan sama untuk semua simpul. Perlu dicatat bahwa sebagian besar implementasi bekerja dengan model (seperti loader atau generator lanskap) menggunakan organisasi segitiga seperti itu, di mana mereka berbagi simpul dengan segitiga lainnya. Dalam kasus seperti itu, pengembang biasanya menggunakan parameter rata-rata di simpul umum, seperti vektor normal, garis singgung dan bi-tangen, untuk mendapatkan hasil yang lebih halus. Segitiga yang membentuk bidang kita juga berbagi beberapa simpul, tetapi karena keduanya terletak pada bidang yang sama, maka rata-rata tidak diperlukan. Meskipun demikian, penting untuk mengingat keberadaan pendekatan semacam itu dalam aplikasi dan tugas nyata.

Vektor tangen dan bi-tangen yang dihasilkan harus memiliki nilai masing-masing (1, 0, 0) dan (0, 1, 0). Itu bersama-sama dengan vektor normal (0, 0, 1) membentuk matriks orthogonal TBN. Jika Anda memvisualisasikan basis yang dihasilkan dengan pesawat, Anda mendapatkan gambar berikut:


Sekarang, setelah menghitung vektor, Anda dapat melanjutkan ke implementasi penuh pemetaan normal.

Pemetaan normal dalam ruang singgung

Pertama, Anda perlu membuat matriks TBN di shader. Untuk tujuan ini, kami akan mentransfer vektor tangen dan bi-tangen yang telah disiapkan sebelumnya ke vertex shader melalui atribut vertex:

 #version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; 

Dalam kode vertex shader itu sendiri, kami membentuk matriks secara langsung:

 void main() { [...] vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); mat3 TBN = mat3(T, B, N) } 

Dalam kode di atas, pertama-tama kita mengkonversi semua vektor basis ruang tangen ke dalam sistem koordinat di mana kita merasa nyaman bekerja - dalam hal ini, ini adalah sistem koordinat dunia dan kami mengalikan vektor dengan model matriks model . Selanjutnya, kita membuat matriks TBN sendiri dengan hanya meneruskan ketiga vektor yang sesuai ke konstruktor tipe mat3 . Harap dicatat bahwa agar urutannya benar sepenuhnya, perlu untuk mengalikan vektor bukan dengan matriks model, tetapi dengan matriks normal, karena kami hanya tertarik pada orientasi vektor, tetapi bukan perpindahan atau penskalaannya

Sebenarnya, tidak perlu mentransfer vektor bi-tangent ke shader.
Karena triple dari vektor TBN saling tegak lurus, bi-tangent dapat ditemukan di shader melalui perkalian vektor:

  vec3 B = cross(N, T) 

Jadi, matriks TBN diterima, bagaimana kita menggunakannya? Sebenarnya, ada dua pendekatan untuk penggunaannya dalam pemetaan normal:

1. Gunakan matriks TBN untuk mengubah semua vektor yang diperlukan dari garis singgung ke ruang dunia. Transfer hasilnya ke fragmen shader, di mana, juga menggunakan matriks, mentransformasikan vektor dari peta normal ke ruang dunia. Akibatnya, vektor normal akan berada di ruang di mana semua pencahayaan dihitung.
2. Ambil matriks invers menjadi TBN dan konversikan semua vektor yang diperlukan dari ruang dunia menjadi tangen. Yaitu gunakan matriks ini untuk mengubah vektor yang terlibat dalam perhitungan pencahayaan menjadi ruang singgung. Vektor normal dalam hal ini juga tetap berada di ruang yang sama dengan peserta lain dalam perhitungan pencahayaan.

Mari kita lihat opsi pertama. Vektor normal dari tekstur yang sesuai ditentukan dalam ruang singgung, sedangkan vektor lain yang digunakan dalam perhitungan pencahayaan didefinisikan dalam ruang dunia. Dengan meneruskan matriks TBN ke fragmen shader, kita dapat mengubah vektor normal yang diperoleh dengan mengambil sampel dari tekstur dari ruang singgung ke dunia, memastikan kesatuan sistem koordinat untuk semua elemen perhitungan pencahayaan. Dalam hal ini, semua perhitungan (terutama perkalian vektor skalar) akan benar.

Transfer matriks TBN dilakukan dengan cara paling sederhana:

 out VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } vs_out; void main() { [...] vs_out.TBN = mat3(T, B, N); } 

Dalam kode shader fragmen, masing-masing, kami menetapkan variabel input tipe mat3:

 in VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } fs_in; 

Memiliki matriks, Anda dapat menentukan kode untuk mendapatkan yang normal dengan ekspresi terjemahan dari tangent ke world space:

 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); normal = normalize(fs_in.TBN * normal); 

Karena normal yang dihasilkan sekarang diatur dalam ruang dunia, tidak perlu mengubah apa pun dalam kode shader. Perhitungan pencahayaan, dan menganggap vektor normal yang diberikan dalam koordinat dunia.

Mari kita juga melihat pendekatan kedua.Ini akan membutuhkan memperoleh matriks TBN terbalik, serta mentransfer semua vektor yang terlibat dalam perhitungan pencahayaan dari sistem koordinat dunia ke yang sesuai dengan vektor normal yang diperoleh dari tekstur - garis singgung. Dalam hal ini, pembentukan matriks TBN tetap tidak berubah, tetapi sebelum beralih ke fragmen shader kita harus mendapatkan matriks terbalik:

 vs_out.TBN = transpose(mat3(T, B, N)); 

Perhatikan bahwa fungsi transpose () digunakan sebagai ganti invers () . Substitusi semacam itu benar, karena untuk matriks ortogonal (di mana semua sumbu diwakili oleh vektor-vektor satuan yang saling tegak lurus), memperoleh matriks invers memberikan hasil yang identik dengan transposisi. Dan ini sangat berguna, karena, dalam kasus umum, menghitung matriks terbalik adalah tugas yang jauh lebih mahal secara komputasi dibandingkan dengan mentransposisi.

Dalam kode shader fragmen, kami tidak akan mengonversi vektor normal, sebaliknya, kami akan mengonversi vektor penting lainnya dari sistem koordinat dunia ke garis singgung, yaitu lightDir dan viewDir. Solusi ini juga membawa semua elemen perhitungan ke dalam sistem koordinat tunggal, kali ini garis singgung.

 void main() { vec3 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos); vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos); [...] } 

Pendekatan kedua tampaknya lebih memakan waktu dan membutuhkan lebih banyak perkalian matriks dalam fragmen shader (yang sangat mempengaruhi kinerja). Mengapa kita bahkan mulai membongkarnya?
Faktanya adalah bahwa menerjemahkan vektor dari koordinat dunia ke garis singgung memberikan keuntungan tambahan: pada kenyataannya, kita dapat memindahkan seluruh kode transformasi dari fragmen ke vertex shader! Pendekatan ini berfungsi karena lightPos dan viewPos tidak berubah dari fragmen ke fragmen, dan nilainya fs_in.FragPoskita juga bisa menerjemahkan ke ruang singgung dalam shader vertex, nilai interpolasi di pintu masuk ke shader fragmen akan cukup benar. Jadi, untuk pendekatan kedua, tidak perlu menerjemahkan semua vektor ini ke ruang singgung dalam kode shader fragmen, sedangkan yang pertama membutuhkannya - normal adalah unik untuk setiap fragmen.

Akibatnya, kami beralih dari mentransfer invers matriks ke TBN ke fragmen shader dan alih-alih memberikannya vektor posisi vertex, sumber cahaya dan pengamat di ruang singgung. Jadi kita akan menyingkirkan multiplikasi matriks yang mahal dalam fragmen shader, yang akan menjadi optimasi yang signifikan, karena vertex shader dieksekusi lebih jarang. Keuntungan inilah yang menempatkan pendekatan kedua dalam kategori penggunaan yang lebih disukai dalam banyak kasus.

 out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform vec3 lightPos; uniform vec3 viewPos; [...] void main() { [...] mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vec3(model * vec4(aPos, 0.0)); 

Di shader fragmen, kami beralih menggunakan variabel input baru dalam perhitungan pencahayaan di ruang singgung. Karena normalnya didefinisikan secara kondisional dalam ruang ini, semua perhitungan tetap benar.
Sekarang semua perhitungan pemetaan normal dilakukan dalam ruang singgung, kita dapat mengubah orientasi permukaan uji dalam aplikasi seperti yang kita inginkan dan pencahayaan akan tetap benar:

 glm::mat4 model(1.0f); model = glm::rotate(model, (float)glfwGetTime() * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0))); shader.setMat4("model", model); RenderQuad(); 

Memang, secara lahiriah semuanya tampak sebagaimana mestinya:


Sumber ada di sini .

Benda kompleks

Jadi, kami menemukan cara melakukan pemetaan normal di ruang singgung dan cara menghitung secara bebas vektor garis singgung dan bias untuk ini. Untungnya, perhitungan manual semacam itu tidak sering menjadi tugas: untuk sebagian besar, kode ini diimplementasikan oleh pengembang di suatu tempat di perut model loader. Dalam kasus kami, ini berlaku untuk loader Assimp yang digunakan .

Assimp menyediakan flag opsi yang sangat berguna saat memuat model: aiProcess_CalcTangentSpace . Ketika diteruskan ke fungsi ReadFile () , perpustakaan itu sendiri akan menghitung garis singgung dan garis singgung dua untuk masing-masing simpul yang dimuat - sebuah proses yang mirip dengan yang dibahas di sini.

 const aiScene *scene = importer.ReadFile( path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace ); 

Setelah itu, Anda dapat langsung mengakses garis singgung yang dihitung:

 vector.x = mesh->mTangents[i].x; vector.y = mesh->mTangents[i].y; vector.z = mesh->mTangents[i].z; vertex.Tangent = vector; 

Anda juga perlu memperbarui kode unduhan untuk memperhitungkan penerimaan peta normal untuk model bertekstur. Format Wavefront Object (.obj) mengekspor peta normal sedemikian rupa sehingga bendera Assimp aiTextureType_NORMAL tidak memastikan bahwa peta ini dimuat dengan benar, sementara semuanya bekerja dengan benar dengan bendera aiTextureType_HEIGHT . Oleh karena itu, secara pribadi, saya biasanya memuat peta normal dengan cara berikut:

 vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal"); 

Tentu saja, pendekatan ini mungkin tidak cocok untuk format deskripsi model lain dan tipe file. Saya juga mencatat bahwa pengaturan flag aiProcess_CalcTangentSpace tidak selalu berfungsi. Kita tahu bahwa perhitungan garis singgung didasarkan pada koordinat tekstur, namun, penulis model sering menerapkan berbagai trik untuk koordinat tekstur, yang memecah perhitungan garis singgung. Jadi, gambar cermin koordinat tekstur sering digunakan untuk model bertekstur simetris. Jika fakta mirroring tidak diperhitungkan, maka perhitungan garis singgung akan salah. Assimp tidak melakukan akuntansi ini. Model nanosuit yang akrab di sini tidak cocok untuk demonstrasi, karena juga menggunakan mirroring.

Tetapi dengan model bertekstur yang benar menggunakan peta normal dan specular, aplikasi tes memberikan hasil yang sangat baik:


Seperti yang Anda lihat, penggunaan pemetaan normal memberikan peningkatan nyata dalam detail dan murah dalam hal biaya kinerja.

Jangan lupa bahwa penggunaan pemetaan normal dapat membantu meningkatkan kinerja untuk adegan tertentu. Tanpa penggunaannya, mencapai detail model hanya dimungkinkan melalui peningkatan kepadatan mesh poligonal. Tetapi teknik ini memungkinkan Anda untuk mencapai tingkat detail yang sama secara visual untuk jerat poli-rendah. Di bawah ini Anda dapat melihat perbandingan dari dua pendekatan ini:


Tingkat detail pada model poli tinggi dan pada model poli rendah menggunakan pemetaan normal secara praktis tidak bisa dibedakan. Jadi teknik ini adalah cara yang bagus untuk mengganti model poli tinggi di tempat kejadian dengan yang disederhanakan dengan hampir tidak ada kerugian dalam kualitas visual.

Komentar terakhir

Ada detail teknis lain mengenai pemetaan normal, yang meningkatkan kualitas sedikit dengan sedikit atau tanpa biaya tambahan.

Dalam kasus di mana garis singgung dihitung untuk jerat besar dan kompleks dengan sejumlah besar simpul yang dimiliki beberapa segitiga, vektor garis singgung biasanya dirata-ratakan untuk mendapatkan hasil pemetaan normal yang halus dan bagus secara visual. Namun, ini menciptakan masalah: setelah rata-rata, triple dari vektor TBN dapat kehilangan saling tegak lurus, yang juga berarti hilangnya ortogonalitas untuk matriks TBN. Dalam kasus umum, hasil pemetaan normal yang diperoleh atas dasar matriks non-ortogonal hanya sedikit salah, tetapi kita masih bisa memperbaikinya.

Untuk melakukan ini, cukup menerapkan metode matematika sederhana:Proses Gram-Schmidt atau re-ortogonisasi dari tiga vektor TBN kami. Dalam kode shader vertex:

 vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); // - T  N T = normalize(T - dot(T, N) * N); //    B    T  N vec3 B = cross(N, T); mat3 TBN = mat3(T, B, N) 

Amandemen ini, walaupun kecil, meningkatkan kualitas pemetaan normal dengan imbalan overhead yang sedikit. Jika Anda tertarik dengan detail prosedur ini, Anda dapat menonton bagian terakhir dari video Pemetaan Matematika Normal, tautan yang diberikan di bawah ini.

Sumber Daya Tambahan

• Tutorial 26: Pemetaan Normal : Pelajaran tentang Pemetaan Normal dari ogldev .
• Cara Kerja Pemetaan Normal : Tutorial video yang menjelaskan dasar-dasar Pemetaan Normal dari TheBennyBox .
• Matematika Pemetaan Normal : Film yang berkaitan dengan yang sebelumnya yang menjelaskan matematika yang digunakan dalam metode Pemetaan Normal, juga dari TheBennyBox .
• Tutorial 13: Pemetaan Normal : pelajaran lain dari opengl-tutorial.org .

PS : Kami punya telegram conf untuk koordinasi transfer. Jika Anda memiliki keinginan serius untuk membantu penerjemahan, maka Anda dipersilakan!