Geekly articles weekly

Dinamika penerbangan vertikal pesawat lebih ringan dari udara

Pendahuluan


Menentukan kecepatan naik dan turunnya pesawat yang lebih ringan dari udara (LALV) hingga saat ini hampir merupakan tugas penting yang muncul dalam desain perangkat tersebut.

Sejumlah besar publikasi dikhususkan untuk LALF, misalnya, hanya pada sumber daya kami ada dua artikel yang sangat menarik [1,2] terkait dengan sejarah pengembangan pada contoh desain khusus kapal udara dan stratostat. Namun, ada sangat sedikit perhitungan dinamika penerbangan vertikal perangkat tersebut, yang memungkinkan setidaknya secara kasar menentukan kecepatan naik dan turunnya SALW.

Pernyataan terakhir membutuhkan penjelasan tertentu, karena pembaca yang berpengalaman ingat kursus fisika sekolah, di mana masalah pada ketinggian naik dan parameter lain dari balon diisi dengan gas lebih ringan dari udara atau oleh udara itu sendiri yang dipanaskan selama penerbangan diselesaikan.

Semua tugas ini didasarkan pada kesetaraan dua kekuatan: gaya berat dan gaya apung. Gas dianggap ideal dan parameternya dihitung menurut hukum Mendeleev Clapeyron. Namun, bahkan perhitungan sederhana dari kekuatan ketiga hambatan udara sudah mengarah ke sistem persamaan diferensial, yang tidak dapat diselesaikan secara analitis. Penting juga untuk memperhitungkan perubahan kepadatan udara atmosfer dengan ketinggian naik dan suhu.

Selain itu, jika Anda perlu mempertimbangkan tidak hanya kenaikan, tetapi juga pembekuan bola dan turun ke tanah, maka itu sama sekali bukan tugas anak-anak. Saya berharap bahwa pertimbangan solusi dari masalah yang sama dengan menggunakan Python tidak hanya akan berkontribusi pada perluasan pengetahuan dalam fisika, tetapi juga mempopulerkan bahasa pemrograman Python itu sendiri. Apa yang saya coba lakukan dalam publikasi saya tentang sumber ini.

Model matematika dari penerbangan LALV dengan cangkang berbentuk bola, volumenya tidak berubah dengan tinggi


Kami membatasi diri untuk mempertimbangkan gerakan pusat massanya di bawah aksi kekuatan berikut: gravitasi ( G ), gaya Archimedean ( Fa ), dan gaya tarik aerodinamis ( Fc ). Kami menulis hubungan untuk menentukan kekuatan melalui parameter gerakan dan lingkungan udara [3]:





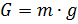
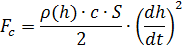
Dalam rumus di atas, notasi yang digunakan: h adalah ketinggian bola, dh / dt adalah kecepatan vertikal, m adalah massa, g adalah percepatan gravitasi, W adalah volume bola, c adalah koefisien bola, c adalah koefisien drag, S adalah area karakteristik resistensi (area midship).
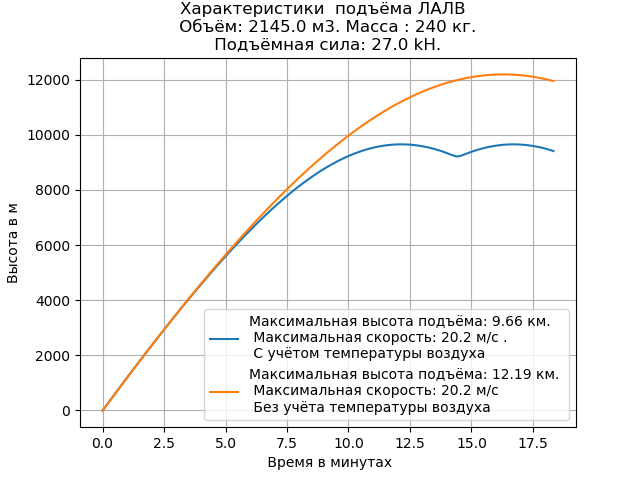
Ketergantungan kepadatan udara pada ketinggian akan dianggap eksponensial:



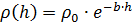
dimana ρ0- kerapatan udara pada ketinggian nol, b - koefisien. Gaya gravitasi diarahkan ke bawah, gaya Archimedean diarahkan ke atas, dan gaya tarik aerodinamik selalu diarahkan "melawan gerakan," oleh karena itu, penyertaan yang benar dari gaya ini dalam persamaan gerak memerlukan pengenalan faktor. −sing(dh/dt).

Namun, untuk tujuan kita, fakta ini tidak penting secara fundamental, dan kami membatasi diri untuk hanya mempertimbangkan tahap mengangkat bola, ketika gaya tarik aerodinamis diarahkan ke bawah dan, oleh karena itu, akan diperhitungkan dalam persamaan gerak dengan tanda minus. Sekarang persamaan gerak dapat ditulis sebagai:

, (1)

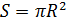
Selain itu, anggaplah bahwa balon adalah benda homogen dengan jari-jari R dengan kepadatan ρb. Kemudian ukuran area yang menentukan hambatan aerodinamisnya didefinisikan sebagai volume sebagai , dan massa, masing-masing, seperti .

Sekarang jelas bahwa setiap istilah persamaan (1) mengandung S. sebagai faktor. Oleh karena itu, setiap istilah persamaan gerak dapat dikurangi dengan faktor S. Persamaan itu sendiri akan mengambil bentuk:

, (2)

Kami memperkenalkan notasi berikut:

;
;

dan menulis ulang (2) dalam bentuk sistem persamaan nonlinier berikut:

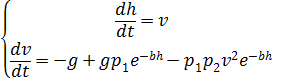
, (3)

Mempengaruhi kecepatan dan tinggi kenaikan suhu udara LALV


Untuk melakukan ini, pertama-tama kita memecahkan sistem (3) menggunakan hubungan berikut untuk ketergantungan kepadatan udara atmosfer pada ketinggian tanpa memperhitungkan suhu akun:



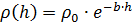
Mari kita ulangi solusi sistem (3), tetapi menggunakan hubungan untuk ketergantungan kepadatan udara pada ketinggian dan suhu:



di mana: b = 0,000125 adalah konstanta yang terkait dengan kepadatan udara 1 / m.;
a = 0,0065 adalah konstanta yang terkait dengan suhu udara dalam K / m.
T0=300K- suhu di permukaan laut.

Daftar program
# -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#   mo=240#   V=(4/3)*pi*R**3 rs=rg+mo/V#    ,  ,   p1=rv/rs#   p2=3*c/(8*R)#   T0=300 def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1*T0/(T0-a*y1))-p1*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,1100,0.01) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title("   \n : %s 3.  : %s . \n  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t/60,y1,label='  : %s . \n  : % s / .\n    '%(round(max(y1)/1000,2),round(max(y2),2))) def fun(y, t): y1, y2= y return [y2,-g+g*p1*exp(-b*y1)-p1*p2*exp(-b*y1)*y2**2] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.plot(t/60,y1,label='  : %s . \n  : % s / \n    '%(round(max(y1)/1000,2),round(max(y2),2))) plt.ylabel('  ') plt.xlabel('   ') plt.legend(loc='best') plt.grid(True) plt.show()


Kami mendapatkan:



Nilai yang dihitung dari ketinggian lift LALV, dengan memperhitungkan suhunya, lebih kecil daripada tanpa memperhitungkan. Kecepatan pengangkatan peralatan tetap tidak berubah.

Penentuan karakteristik semua fase penerbangan SALV dari awal hingga pendaratan


Untuk membangun program penerbangan, LALV mempertimbangkan kondisi untuk periode waktu berikut:

Bangkit - ;
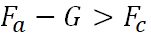
Menggantung - ;
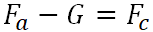
Pendaratan - .

Daftar program
 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. R=8#     . b=0.000125# ,      1/ a=6.5*10**-3# ,      / c=0.4#    mo=240#    V=(4/3)*pi*R**3 p2=3*c/(8*R)#   T0=300#     tz=4000#     rgu=1.2#         /3 tz=4000#   def fun(y, t): y1,y2= y if y2<=0: if t<tz: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] elif t>=tz: return [y2,-g+g*(rv/(rgu+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rgu+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] else: return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))-(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2] t =arange(0,tz+555,0.1) y0 = [0.0,0.0] [y1,y2]=odeint(fun, y0,t, full_output=False).T plt.title(", ,   \n      \n : %s 3.  : %s .  : %s k. "%(round(V,0),mo,round(0.001*g*rv*V,0))) plt.plot(t,y1,label='  : %s . \n  : % s / .\n   %s .'%(round(max(y1)/1000,2), round(max(y2),2),tz-2*555)) plt.ylabel('  ') plt.xlabel('   .') plt.legend(loc='best') plt.grid(True) plt.show()


Kami mendapatkan:



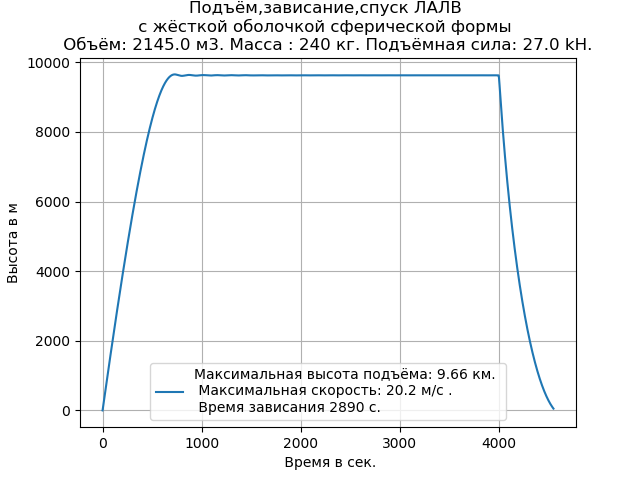
Sebagai berikut dari grafik dan daftar program, untuk melakukan eksperimen komputasi, cukup memasukkan data awal yang diperlukan.

Model matematika dari penerbangan LALV dengan cangkang, volumenya bervariasi dengan tinggi


LALV tersebut termasuk stratostats. Balon stratosfer tidak dapat sepenuhnya dipompa dengan helium, sehingga memberikan gaya angkat maksimum, yang akan mengubah bentuk cangkangnya menjadi bola. Bola seperti itu di ketinggian bisa meledak karena meningkatnya perbedaan tekanan internal dan eksternal.

Untuk alasan ini, untuk menghitung ketinggian lift maksimum yang dapat dicapai, dua nilai volumenya diperkenalkan: masing-masing minimum Vmin dan maksimum Vmax. Dengan mempertimbangkan variabel yang diperkenalkan dan ketergantungan kepadatan udara pada ketinggian, rasio untuk gaya apung Fa dan gaya gravitasi Ft mengambil bentuk:

, (4)

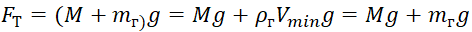
, (5)

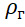
di mana: M adalah massa cangkang dan peralatan balon stratosfer; Adalah densitas helium.

Menyamakan hubungan (4) dan (5), dengan asumsi bahwa volume shell V adalah fungsi dari ketinggian LALV, kami memperoleh rasio:

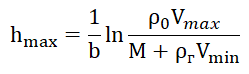
. (6)

Nilai numerik dari parameter yang termasuk dalam relasi (6) diberikan dalam daftar untuk membuat grafik, yang hanya diberikan untuk tujuan yang ditunjukkan.

Membuat daftar grafik dengan data
 # -*- coding: utf8 -*- from numpy import* from scipy.integrate import odeint import matplotlib.pyplot as plt g=9.81#       /2. rv=1.29#     /3. rg=0.17#    /3. Vmin=400#    /3. b=0.000128# ,      1/. c=0.8#   mo=40#   rs=rg+mo/Vmin#    ,     p1=rv/rs#   h=[(10**-3)*log((rv*w)/(mo+rg*Vmin))*b**-1 for w in arange(1*10**3,1.8*10**5,1000)] v=[(10**-3)*w for w in arange(1*10**3,1.8*10**5,1000)] plt.title("     \n    ") plt.plot(v,h) plt.xlabel('    . 3') plt.ylabel('     .') plt.grid(True) plt.show()


Kami mendapatkan:



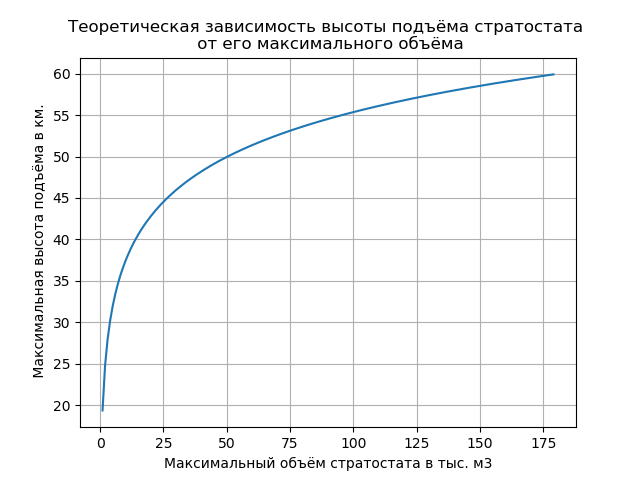
Dengan mengubah parameter LALV yang tercantum dalam daftar program, Anda bisa mendapatkan grafik yang diberikan dan memilih volume shell maksimum yang diperlukan selama desain. Penyempurnaan hasil dilakukan dengan menggunakan pengalaman luas dalam pembuatan perangkat tersebut.

Kesimpulan:

  1. Model matematika dari dua jenis pesawat yang lebih ringan daripada udara diperoleh, yang memungkinkan eksperimen komputasi untuk mengevaluasi parameter perangkat tersebut dalam kondisi ideal lingkungan udara.
  2. Skema multi-tahap yang diusulkan untuk solusi numerik dari sistem persamaan diferensial memungkinkan seseorang untuk mendapatkan lintasan vertikal pesawat yang lebih ringan daripada udara pada tahap kenaikan melayang dan turun.

Referensi


  1. Beberapa kata tentang kapal udara
  2. Dalam perjalanan ke luar angkasa. Stratostats
  3. Ryzhikov Yu.I. Fortran modern. - St. Petersburg: Cetak mahkota, 2004 .-- 288 hal.

Source: https://habr.com/ru/post/id415623/

More articles:


All Articles