AI, tentu saja praktis. Tinjauan jaringan saraf untuk klasifikasi gambar

Artikel ini menyediakan tinjauan teoritis yang dapat diakses dari jaringan saraf convolutional (CNN) dan menjelaskan aplikasi mereka untuk masalah klasifikasi gambar.

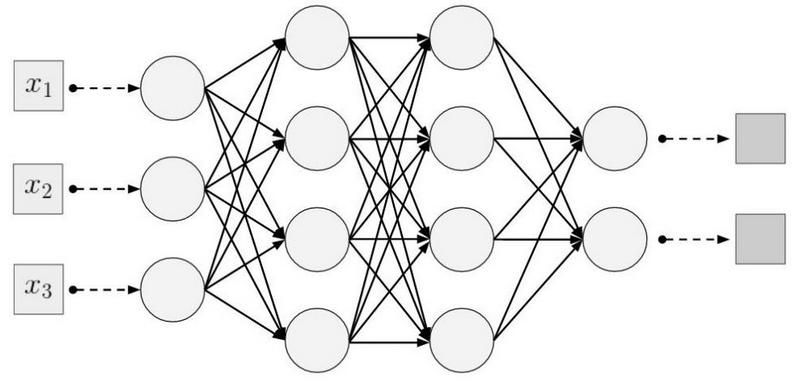
Pendekatan Umum: Tidak Mendalam Pembelajaran

Istilah "pemrosesan gambar" mengacu pada kelas tugas yang luas dimana data input adalah gambar, dan outputnya dapat berupa gambar atau set fitur karakteristik terkait. Ada banyak pilihan: klasifikasi, segmentasi, anotasi, deteksi objek, dll. Dalam artikel ini, kami memeriksa klasifikasi gambar, tidak hanya karena itu adalah tugas yang paling sederhana, tetapi juga karena itu mendasari banyak tugas lainnya.

Pendekatan umum untuk klasifikasi gambar terdiri dari dua langkah berikut:

1. Generasi fitur gambar yang signifikan.
2. Klasifikasi gambar berdasarkan atributnya.

Urutan operasi yang umum menggunakan model sederhana seperti MultiLayer Perceptron (MLP), Support Vector Machine (SVM), k metode tetangga terdekat dan regresi logistik di atas fitur yang dibuat secara manual. Atribut dihasilkan menggunakan berbagai transformasi (mis., Deteksi skala abu-abu dan ambang batas) dan deskriptor, mis., Histogram Berorientasi Gradien ( HOG ) atau transformasi Feature Transform ( SIFT ) skala-invarian, dan dll.

Keterbatasan utama dari metode yang diterima secara umum adalah partisipasi seorang ahli dalam memilih satu set dan urutan langkah-langkah untuk menghasilkan fitur.

Seiring waktu, diketahui bahwa sebagian besar teknik untuk menghasilkan fitur dapat digeneralisasi menggunakan kernel (filter) - matriks kecil (biasanya berukuran 5 × 5), yang merupakan konvolusi dari gambar asli. Konvolusi dapat dianggap sebagai proses dua tahap berurutan:

1. Lewati inti tetap yang sama ke seluruh gambar sumber.
2. Pada setiap langkah, hitung produk skalar dari kernel dan gambar asli di lokasi kernel saat ini.

Hasil konvolusi gambar dan kernel disebut peta fitur.
Penjelasan yang lebih matematis diberikan dalam bab yang relevan dari buku yang baru diterbitkan, Deep Learning, oleh I. Goodfellow, I. Benjio, dan A. Courville.


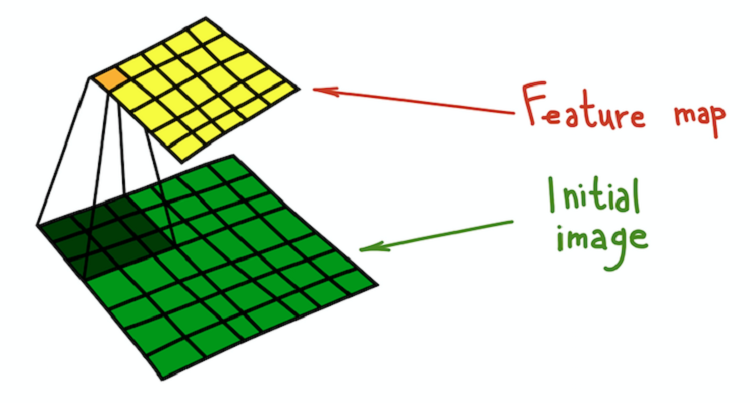Proses konvolusi inti (hijau tua) dengan gambar asli (hijau), akibatnya fitur peta diperoleh (kuning).

Contoh sederhana dari transformasi yang dapat dilakukan dengan filter adalah mengaburkan gambar. Ambil filter yang terdiri dari semua unit. Ini menghitung rata-rata lingkungan yang ditentukan oleh filter. Dalam hal ini, lingkungan adalah bagian persegi, tetapi bisa berupa salib atau apa pun. Rata-rata menyebabkan hilangnya informasi tentang posisi tepat objek, sehingga mengaburkan seluruh gambar. Penjelasan intuitif yang serupa dapat diberikan untuk setiap filter yang dibuat secara manual.


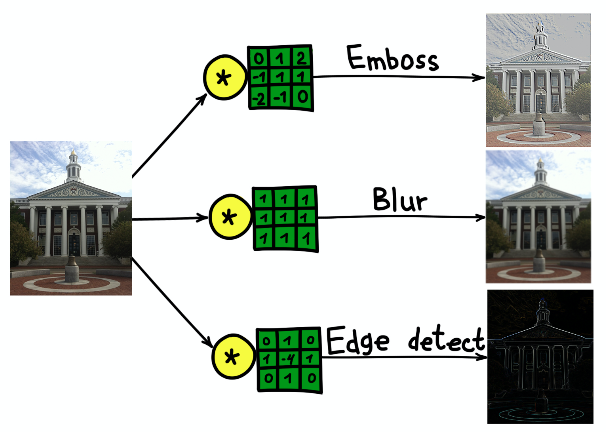Hasil konvolusi gambar gedung Universitas Harvard dengan tiga core berbeda.

Jaringan Saraf Konvolusional

Pendekatan konvolusional untuk klasifikasi gambar memiliki sejumlah kelemahan signifikan:

• Proses multi-langkah alih-alih urutan ujung ke ujung.
• Filter adalah alat generalisasi yang bagus, tetapi mereka adalah matriks yang diperbaiki. Bagaimana cara memilih bobot dalam filter?

Untungnya, filter yang dapat dipelajari telah ditemukan, yang merupakan prinsip dasar yang mendasari CNN. Prinsipnya sederhana: Kami akan melatih filter yang diterapkan pada deskripsi gambar untuk memenuhi tugas mereka.

CNN tidak memiliki satu penemu, tetapi salah satu kasus pertama dari aplikasi mereka adalah LeNet-5 * dalam karya “ Pembelajaran Berbasis Gradien yang Diterapkan pada Pengakuan Dokumen” oleh I. LeCun dan yang lainnya penulis.

CNN membunuh dua burung dengan satu batu: tidak ada kebutuhan untuk definisi awal filter, dan proses pembelajaran menjadi ujung ke ujung. Arsitektur CNN tipikal terdiri dari bagian-bagian berikut:

• Lapisan konvolusional
• Berlapis-lapis lapisan
• Lapisan padat (terhubung penuh)

Mari kita bahas masing-masing bagian secara lebih rinci.

Lapisan konvolusional

Lapisan convolutional adalah elemen struktural utama dari CNN. Lapisan konvolusional memiliki seperangkat karakteristik:
Konektivitas lokal (jarang) . Dalam lapisan padat, setiap neuron terhubung ke masing-masing neuron dari lapisan sebelumnya (karena itu mereka disebut padat). Pada lapisan konvolusional, setiap neuron terhubung hanya dengan sebagian kecil dari neuron pada lapisan sebelumnya.


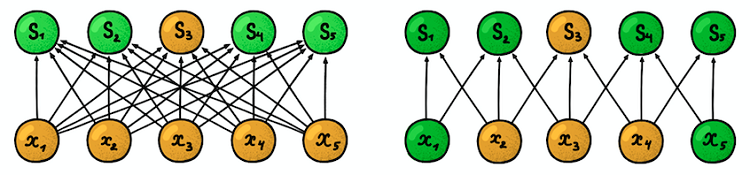Contoh jaringan saraf satu dimensi. (kiri) Koneksi neuron dalam jaringan padat yang khas, (kanan) Karakterisasi konektivitas lokal yang melekat pada lapisan convolutional. Gambar diambil dari I. Goodfellow dan lainnya oleh Deep Learning

Ukuran area di mana neuron terhubung disebut ukuran filter (panjang filter dalam kasus data satu dimensi, misalnya deret waktu, atau lebar / tinggi dalam kasus data dua dimensi, misalnya gambar). Pada gambar di sebelah kanan, ukuran filter adalah 3. Bobot yang digunakan untuk membuat sambungan disebut filter (vektor dalam hal data satu dimensi dan matriks untuk data dua dimensi). Langkahnya adalah jarak filter bergerak di atas data (pada gambar di sebelah kanan, langkahnya adalah 1). Gagasan konektivitas lokal tidak lebih dari sebuah kernel yang bergerak satu langkah. Setiap neuron tingkat konvolusional mewakili dan mengimplementasikan satu posisi spesifik dari nukleus yang meluncur di sepanjang gambar asli.


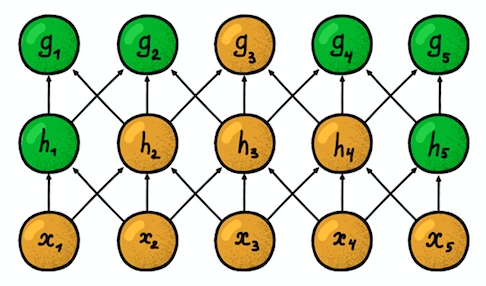Dua lapisan konvolusional satu dimensi yang berdekatan

Properti penting lainnya adalah apa yang disebut zona kerentanan . Ini mencerminkan jumlah posisi dari sinyal asli yang dapat “dilihat” oleh neuron saat ini. Misalnya, zona kerentanan lapisan jaringan pertama, yang ditunjukkan pada gambar, sama dengan ukuran filter 3, karena setiap neuron terhubung hanya dengan tiga neuron dari sinyal asli. Namun, pada lapisan kedua, zona kerentanan sudah 5, karena neuron lapisan kedua mengumpulkan tiga neuron dari lapisan pertama, yang masing-masing memiliki zona kerentanan 3. Dengan meningkatnya kedalaman, zona kerentanan tumbuh secara linear.

Parameter bersama . Ingatlah bahwa dalam pemrosesan gambar klasik, inti yang sama meluncur di seluruh gambar. Gagasan yang sama berlaku di sini. Kami hanya memperbaiki ukuran filter bobot untuk satu lapisan dan kami akan menerapkan bobot ini untuk semua neuron di lapisan. Ini sama dengan menggeser inti yang sama di seluruh gambar. Tetapi mungkin timbul pertanyaan: bagaimana kita bisa belajar sesuatu dengan sejumlah kecil parameter?


Panah gelap mewakili bobot yang sama. (kiri) MLP Reguler, di mana setiap faktor pembobotan adalah parameter yang terpisah, (kanan) Contoh pemisahan parameter, di mana beberapa faktor pembobotan menunjukkan parameter pelatihan yang sama

Struktur ruang Jawaban atas pertanyaan ini sederhana: kami akan melatih beberapa filter dalam satu lapisan! Mereka ditempatkan sejajar satu sama lain, sehingga membentuk dimensi baru.

Kami berhenti sebentar dan menjelaskan ide yang disajikan oleh contoh gambar RGB dua dimensi dari 227 × 227. Perhatikan bahwa di sini kita berurusan dengan gambar input tiga saluran, yang, pada dasarnya, berarti bahwa kita memiliki tiga gambar input atau data input tiga dimensi.


Struktur spasial dari gambar input

Kami akan mempertimbangkan dimensi saluran sebagai kedalaman gambar (perhatikan bahwa ini tidak sama dengan kedalaman jaringan saraf, yang sama dengan jumlah lapisan jaringan). Pertanyaannya adalah bagaimana menentukan kernel untuk kasus ini.


Contoh inti dua dimensi, yang pada dasarnya adalah matriks tiga dimensi dengan pengukuran kedalaman tambahan. Filter ini memberikan konvolusi dengan gambar; yaitu, meluncur di atas gambar di luar angkasa, menghitung produk skalar

Jawabannya sederhana, meskipun masih belum jelas: kita akan membuat kernel juga tiga dimensi. Dua dimensi pertama akan tetap sama (lebar dan tinggi inti), dan dimensi ketiga selalu sama dengan kedalaman data input.


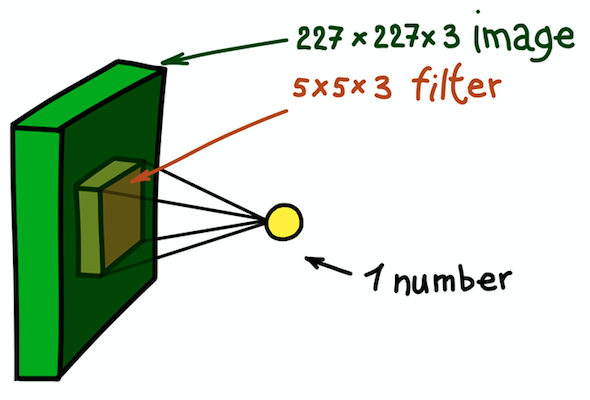Contoh langkah konvolusi spasial. Hasil produk skalar dari filter dan sebagian kecil dari gambar 5 × 5 × 3 (mis., 5 × 5 × 5 + 1 = 76, dimensi produk skalar + shift) adalah satu angka

Dalam hal ini, seluruh bagian 5 × 5 × 3 dari gambar asli diubah menjadi satu angka, dan gambar tiga dimensi itu sendiri akan diubah menjadi peta fitur ( peta aktivasi ). Peta fitur adalah seperangkat neuron, yang masing-masing menghitung fungsinya sendiri, dengan mempertimbangkan dua prinsip dasar yang dibahas di atas: konektivitas lokal (setiap neuron dikaitkan dengan hanya sebagian kecil dari data input) dan pemisahan parameter (semua neuron menggunakan filter yang sama). Idealnya, peta fitur ini akan sama dengan yang sudah ditemukan pada contoh jaringan yang diterima secara umum - ini menyimpan hasil konvolusi dari gambar input dan filter.


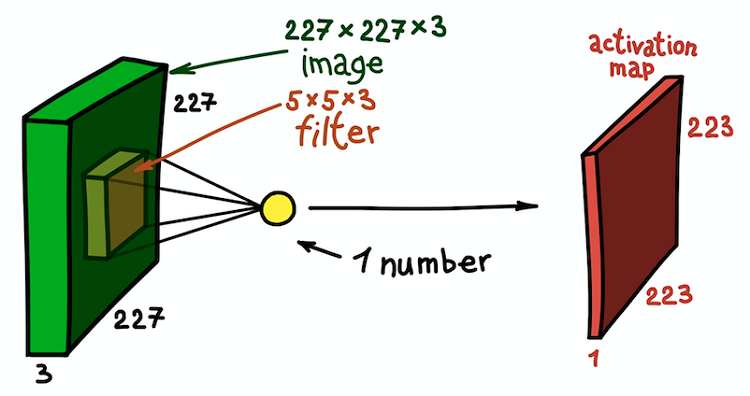Peta fitur sebagai hasil konvolusi inti dengan semua posisi spasial

Perhatikan bahwa kedalaman peta fitur adalah 1, karena kami hanya menggunakan satu filter. Tetapi tidak ada yang mencegah kita menggunakan lebih banyak filter; misalnya, 6. Semuanya akan berinteraksi dengan input data yang sama dan akan bekerja secara independen satu sama lain. Mari kita melangkah lebih jauh dan menggabungkan kartu fitur ini. Dimensi spasialnya sama karena dimensi filternya sama. Dengan demikian, peta fitur yang dikumpulkan bersama dapat dianggap sebagai matriks tiga dimensi baru, dimensi kedalaman yang diwakili oleh peta fitur dari core yang berbeda. Dalam hal ini, saluran RGB dari gambar input tidak lain adalah tiga peta fitur asli.


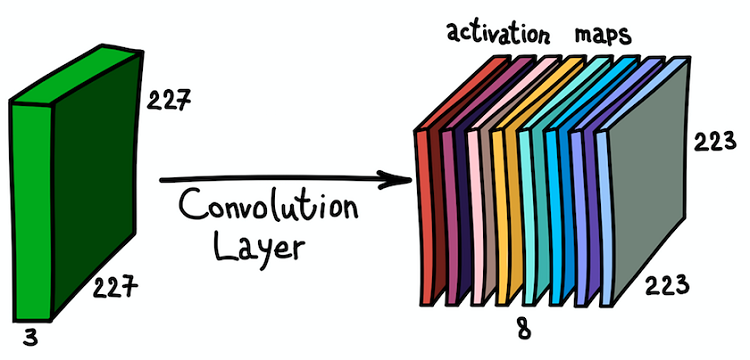Aplikasi paralel dari beberapa filter ke gambar input dan set kartu aktivasi yang dihasilkan

Pemahaman tentang peta fitur dan kombinasinya sangat penting, karena, setelah menyadari hal ini, kami dapat memperluas arsitektur jaringan dan memasang lapisan konvolusional satu di atas yang lain, sehingga meningkatkan zona kerentanan dan memperkaya pengklasifikasi kami.


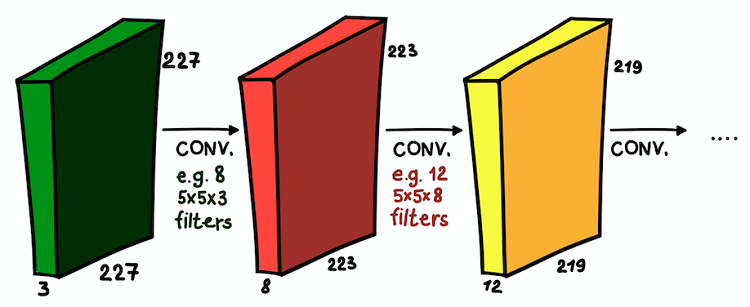Lapisan konvolusional dipasang di atas satu sama lain. Di setiap lapisan, ukuran filter dan jumlahnya dapat bervariasi

Sekarang kita mengerti apa itu jaringan konvolusional. Tujuan utama dari lapisan-lapisan ini adalah sama dengan pendekatan yang diterima secara umum - untuk mendeteksi tanda-tanda signifikan dari gambar. Dan, jika pada lapisan pertama tanda-tanda ini bisa sangat sederhana (adanya garis vertikal / horizontal), kedalaman jaringan meningkatkan tingkat abstraksi mereka (keberadaan anjing / kucing / orang).

Berlapis-lapis lapisan

Lapisan konvolusional adalah blok bangunan utama CNN. Tetapi ada bagian penting dan sering digunakan lainnya - ini adalah lapisan subsampel. Dalam pemrosesan gambar konvensional, tidak ada analog langsung, tetapi subsampel dapat dianggap sebagai jenis kernel lain. Apa ini


Contoh subsampling. (kiri) Bagaimana subsampel mengubah ukuran susunan data spasial (tetapi bukan saluran!), (kanan) Skema dasar cara kerja subsampel

Subsampel menyaring sebagian lingkungan dari setiap piksel dari data input dengan fungsi agregasi tertentu, misalnya, maksimum, rata-rata, dll. Subsampel pada dasarnya sama dengan konvolusi, tetapi fungsi penggabungan piksel tidak terbatas pada produk skalar. Perbedaan penting lainnya adalah bahwa subsampling hanya berfungsi dalam dimensi spasial. Fitur karakteristik dari lapisan sub-sampel adalah bahwa pitch biasanya sama dengan ukuran filter (nilai tipinya adalah 2).

Subsampel memiliki tiga tujuan utama:

• Mengurangi dimensi spasial, atau sub-sampling. Ini dilakukan untuk mengurangi jumlah parameter.
• Pertumbuhan zona kerentanan. Karena neuron subsampel di lapisan berikutnya, lebih banyak langkah dari sinyal input diakumulasikan
• Invariansi translasi ke heterogenitas kecil pada posisi pola dalam sinyal input. Dengan menghitung statistik agregasi dari lingkungan kecil dari sinyal input, subsampel dapat mengabaikan perpindahan spasial kecil di dalamnya.

Lapisan tebal

Lapisan konvolusional dan lapisan subsampel melayani tujuan yang sama - menghasilkan atribut gambar. Langkah terakhir adalah untuk mengklasifikasikan gambar input berdasarkan fitur yang terdeteksi. Di CNN, lapisan padat di atas jaringan melakukan ini. Bagian dari jaringan ini disebut klasifikasi . Itu dapat berisi beberapa lapisan di atas satu sama lain dengan konektivitas lengkap, tetapi biasanya berakhir dengan lapisan kelas softmax diaktifkan oleh fungsi aktivasi logistik multi-variabel, di mana jumlah blok sama dengan jumlah kelas. Pada output dari lapisan ini adalah distribusi probabilitas oleh kelas untuk objek input. Sekarang gambar dapat diklasifikasikan dengan memilih kelas yang paling mungkin.