"Tapi kita membuat roket!"

Dalam artikel sebelumnya, saya memeriksa apakah mungkin untuk secara otomatis menyesuaikan kontroler fuzzy menggunakan "metode standar" optimasi. Ternyata dimungkinkan dan hasil tuning otomatis cukup memuaskan. Setidaknya untuk roket yang modelnya digunakan.

Untuk objek kontrol non-stasioner di mana parameter objek bervariasi pada rentang lebar, pengontrol fuzzy mungkin tidak memberikan kualitas kontrol yang memadai di semua rentang operasi. Dalam hal ini, perlu untuk menggunakan kontroler fuzzy dengan "tuning multi-channel".

Mari kita periksa apakah mungkin untuk mengkonfigurasi regulator seperti itu menggunakan metode optimasi standar.
Pertimbangkan sintesis pengontrol fuzzy dengan tuning multi-saluran untuk menstabilkan rudal balistik di sudut pitch. Seperti yang diminta dalam komentar, rudal akan menjadi FAU-2. Kami menggunakan contoh dari buku yang sama oleh V. Gostev. "Regulator fuzzy dalam sistem kontrol otomatis."

Semua istilah yang digunakan dalam teks ini diambil dari buku ini dan mungkin tidak sesuai dengan terminologi yang ketat dari teori kontrol otomatis.

Pernyataan masalah

Sebuah rudal balistik yang menggunakan sejumlah besar sistem kontrol lokal adalah objek kontrol yang pada dasarnya tidak stasioner. Fungsi transfer, yang menggambarkan roket sebagai objek kontrol, berbeda dari fungsi transfer pesawat bersayap karena memiliki hubungan yang tidak stabil, sehingga gerakan roket yang tidak terkontrol di sepanjang jalur yang diprogram akan menjadi tidak stabil.

Di bawah ini kami mempertimbangkan sistem stabilisasi rudal balistik dalam sudut pitch (saluran gerak memanjang). Sistem terdiri dari elemen-elemen yang diperlukan secara fungsional berikut:
elemen perbandingan (gyro bebas dengan sensor potensiometri yang ditandai dengan koefisien Kp);
power amplifier Ku, dan perangkat kemudi hidrolik.

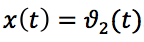
Mengambil sudut pitch sebagai koordinat keluar roket , untuk koordinat input - sudut kemudi , kami mendefinisikan fungsi transfer dalam bentuk:


(Roda kemudi dan roket analog termasuk dalam objek kontrol) Parameter fungsi transfer akan bergantung pada polinomial waktu. Secara matematis, mereka dapat ditentukan oleh polinomial:











Tugas mengasumsikan bahwa waktu mulai penerbangan adalah 6 detik. Nilai polinomial diterima dengan pergeseran 6 detik.
Model matematika dari tautan osilasi non-stasioner dijelaskan oleh persamaan diferensial:



Model matematika dari tautan paksa tidak stabil dijelaskan oleh persamaan diferensial:



Kesalahan ketidakcocokan pada input kontroler fuzzy adalah perbedaan antara set dan sudut pitch yang diperlukan.

Diagram struktural model ditunjukkan pada Gambar 1. Untuk memahami prinsip pembentukan model, jalur komunikasi menunjukkan variabel X1, X dan turunannya ( X1 '', X1 '', X ' ) sesuai dengan persamaan tautan. Kotak hijau menunjukkan bagian dari rangkaian model yang sesuai dengan tautan berosilasi, dan yang kuning adalah tautan pemaksa.

Parameter a (t), b (t), c (t), r (t) diatur dalam bentuk faktor amplifikasi, dalam blok tipe "amplifier". Parameter diatur dalam gain tautan integrasi.


Gambar 1. Diagram struktural model.

Jalur perangkat lunak, diberi sudut nada u (t) = 1 + 0,5sin (/t / 30).
Grafik perubahan dalam parameter roket selama penerbangan disajikan pada Gambar 2.
Nilai t = 6 diambil sebagai awal penerbangan, dalam fungsi polinomial, nilai (waktu + 6) digunakan untuk menghitung parameter, di mana waktu adalah waktu simulasi saat ini.


Gambar 2. Grafik perubahan parameter roket.

Pengontrol logika fuzzy

Sebagai pengontrol yang didasarkan pada logika fuzzy, kami menggunakan pengontrol yang ditunjukkan pada Gambar 3. Ketidakcocokan antara sudut pitch yang diberikan dan sudut pitch rudal nyata diterapkan pada input.

Blok delay per langkah kuantisasi memberikan diskritisasi konversi sinyal kontinu menjadi sinyal diskrit dengan langkah pengambilan sampel 0,01 detik.

Dengan menggunakan dua penundaan lagi, penyimpangan turunan pertama dan kedua dihitung dengan metode perbedaan pada langkah diskritisasi.

Unit pentahapan menghitung nilai-nilai istilah untuk penyimpangan, laju perubahan dan percepatan. (Untuk lebih lanjut tentang ini, lihat teks sebelumnya ). Di pintu keluar dari setiap blok pentahapan, kami memperoleh vektor istilah untuk variabel linguistik. (lihat tabel 1)

Variabel linguistik	Ketentuan
Penyimpangan	Lebih banyak Norma Lebih sedikit
Tingkat perubahan	Tumbuh Tidak berubah Jatuh
Perubahan lebih cepat	Meningkat Konstan Menurun

Blok demultiplexer mengurai vektor menjadi istilah terpisah, yang ditransmisikan ke blok pemrosesan logis sesuai dengan aturan inferensi fuzzy.
Hasil inferensi fuzzy juga memiliki tiga variabel linguistik: "mengurangi", "tidak berubah", "meningkat". Aturan inferensi berikut ditulis dalam bentuk diagram.

• Jika Lebih Banyak dan Bertumbuh dan tingkat pertumbuhan meningkat => berkurang .
• Jika norma , dan tidak berubah dan konstan => kita tidak berubah .
• Jika Less and Falls dan tingkat jatuh meningkat => meningkat .

Gambar 3. Skema regulator berdasarkan logika fuzzy.

Dalam denazifikasi, fungsi segitiga dengan basis umum digunakan sebagai fungsi keanggotaan (lihat Gambar. 4)

Gambar 4. Fungsi pentahapan segitiga dengan basis bersama.

Diasumsikan bahwa fungsinya simetris terhadap 0, dalam hal ini, untuk menggambarkan tiga fungsi segitiga, satu nilai Max sudah cukup. Untuk yang ditunjukkan pada gambar, Max = 30.

Fungsi keanggotaan yang sama digunakan untuk output.

Untuk definisi lengkap dari regulator, perlu menetapkan nilai maksimum untuk blok variabelisasi fase:

- deltaMax - penyimpangan maksimum;
- divMax - turunan maksimum dari penyimpangan;
- div2Max - turunan kedua maksimum dari penyimpangan;
- uMax - aksi kontrol maksimum.

Optimasi proses penuh

Tindakan kontrol maksimum diambil sama dengan uMax - 70.
Jadi, tetap bagi kita untuk memilih 3 parameter untuk fungsi pemindahan fase.
Dalam masalah ini, ketidakcocokan diumpankan oleh langkah pada saat nol waktu model, u (t) = 1 + 0,5.sin (πt / 30).

Lintasan terprogram, sudut pitch yang diberikan u (t) = 1 + 0,5sin (/t / 30), menyebabkan efek bertahap pada detik pertama proses transisi, karena ternyata selama percobaan dengan tugas sebelumnya, pengendali yang disetel ke proses kontrol yang lancar, dengan tindakan bertahap, dapat tidak memberikan kualitas yang diperlukan dari proses transisi.

Karena itu, untuk optimasi, kami membentuk 3 kriteria:

1. Waktu sementara - kita harus mencapai jalur program yang diberikan secepat mungkin.
2. Simpangan baku.
3. Jumlah pergantian - dalam percobaan dengan tugas sebelumnya, kami mendapatkan opsi ketika ada osilasi frekuensi tinggi dari aksi kontrol pada output dalam sistem kontrol.

Skema umum dari blok optimasi ditunjukkan pada Gambar 5.

Gambar 5. Skema blok optimisasi.

Parameter masukan blok pengoptimalan:

- penyimpangan dari sudut pitch yang diberikan.
- dampak regulasi.

Untuk menghitung waktu sementara, sebuah saklar digunakan di mana waktu model saat ini diterapkan ke salah satu input. Setelah blok ada penundaan untuk periode kuantisasi, nilai dari penundaan ditransmisikan ke input kedua.

Sebagai saklar, modul deviasi digunakan. Jika modul deviasi lebih besar dari nilai switching yang ditetapkan (0,02), maka waktu saat ini adalah output di blok, jika modul kurang dari nilai yang ditetapkan, waktu yang disimpan ketika deviasi lebih besar ditransmisikan ke output. Jika deviasi lebih jauh lagi melebihi batas, kita kembali mendapatkan waktu. Jadi, di pintu keluar kita selalu memiliki waktu terakhir ketika deviasi melebihi nilai yang ditetapkan.
Sebagai unit switching, tanda aksi kontrol diubah dari + ke -. Untuk menghitung jumlah pergantian, kami menggunakan blok "impuls sepanjang bagian depan" yang, ketika input diubah dari 0 ke 1, memberikan durasi pulsa pada langkah integrasi, impuls dihitung oleh integrator. Di pintu keluar dari blok - jumlah switching.

- Blok optimisasi memilih nilai parameter yang akan dioptimalkan sedemikian rupa untuk meminimalkan ketiga parameter:
- deltaMax - penyimpangan maksimum;
- divMax - turunan maksimum dari penyimpangan;
- div2Max - turunan kedua maksimum dari penyimpangan.

Hasilnya adalah optimalisasi proses transisi yang lengkap.

Setelah memulai proses pengoptimalan, kami memperoleh parameter optimal berikut untuk pengontrol fuzzy:

- deltaMax = 0.185– penyimpangan maksimum;
- divMax = 0.278 - turunan maksimum dari penyimpangan;
- div2Max = 1.291 - turunan maksimum kedua dari penyimpangan.

Hasil dari proses yang dioptimalkan ditunjukkan pada Gambar 6.

Gambar 6a. Proses transisi.

Gambar 6b. Opsi kontrol.

Dapat dilihat bahwa optimasi, secara keseluruhan, adalah sukses, tetapi penyimpangan dari sudut nada yang diberikan ada hampir di seluruh proses. Grafik deviasi yang diperbesar menunjukkan bahwa penyimpangan setelah optimasi dan penyelesaian proses transisi berada di kisaran 0,015 - 0,02. (lihat gambar 7)

Gambar 7. Penyimpangan dalam proses kontrol.

Optimalisasi berdasarkan bagian penerbangan.

Mari kita coba untuk meningkatkan proses dengan memilih parameter dari pengontrol fuzzy untuk berbagai bagian dari penerbangan roket.

Bagian pertama adalah waktu dari awal untuk keluar di jalur yang diberikan. Berdasarkan grafik deviasi, proses transisi yang terkait dengan efek stepwise awal berakhir di suatu tempat di 20 detik. (lihat gbr. 7). Di bagian ini, optimasi waktu proses transisi terjadi.

Atur waktu akhir perhitungan menjadi 20 detik. Dan kami akan melakukan optimasi, menghapus standar deviasi dari kriteria. Kami akan mengoptimalkan pada saat proses transisi dan jumlah switching. Diagram blok optimasi ditunjukkan pada Gambar 8.


Gambar 8. Skema optimisasi pada fase pertama penerbangan.

Optimalisasi otomatis untuk fase pertama penerbangan hingga 20 detik menghasilkan parameter berikut untuk regulasi fuzzy:

- deltaMax = 0,056– deviasi maksimum;
- divMax = 0,0968 - turunan maksimum dari penyimpangan;
- div2Max = 0,987 - turunan maksimum kedua dari penyimpangan.

Proses transisi setelah optimasi ditunjukkan pada Gambar 9.

Penyimpangan pada skala yang lebih besar ditunjukkan pada Gambar 10.

Gambar 9a. Proses transisi.

Gambar 9b. Opsi kontrol.

Gambar 10. Deviasi skala yang lebih besar dari kaki pertama penerbangan.

Grafik menunjukkan bahwa overshoot berkurang dan deviasi setelah akhir proses transisi menjadi kurang dari 0,005.

Untuk optimasi di bagian penerbangan berikutnya, kami akan melakukan simulasi dengan keadaan tersimpan yang diperoleh di bagian pertama.

Simulasi berlangsung dari 20 hingga 40 detik penerbangan rudal balistik, optimasi terjadi sepanjang proses.

Karena kami telah menyelesaikan proses transisi di awal bagian kedua, kami melakukan optimasi hanya dengan penyimpangan dan jumlah sakelar. Diagram blok optimasi ditunjukkan pada Gambar 11.


Gambar 11. Skema optimisasi untuk bagian penerbangan kedua.

Optimalisasi otomatis untuk penerbangan fase kedua dari 20 hingga 40 detik menghasilkan parameter berikut untuk pengaturan fuzzy:

- deltaMax = 0,056– deviasi maksimum;
- divMax = 0,0974 - turunan maksimum dari penyimpangan;
- div2Max = 0,980 - turunan kedua maksimum dari penyimpangan.

Dengan parameter yang diberikan, deviasi sudut pitch dari yang diberikan berkurang selama seluruh bagian waktu penerbangan kedua. Tetapi jika kita menggunakan parameter yang diperoleh dengan optimasi di bagian kedua penerbangan untuk mengendalikan hingga 66 detik, maka dapat dilihat bahwa keakuratannya mulai berkurang dan deviasi mulai meningkat setelah 40 detik (lihat Gambar 12).


Gambar 12. Proses kontrol rudal balistik dengan pengaturan yang dioptimalkan untuk penerbangan 20-40 detik.

Ulangi pengoptimalan untuk penerbangan ketiga. Simpan hasilnya selama 40 detik.

Kami menggunakannya untuk memulai dan mengoptimalkan dalam bagian dari 40 hingga 66 detik.

Optimalisasi otomatis untuk bagian penerbangan terakhir dari 40 hingga 66 detik menghasilkan parameter berikut untuk regulasi fuzzy:

- deltaMax = 0,0146– penyimpangan maksimum;
- divMax = 0,0157– turunan maksimum dari penyimpangan;
- div2Max = 0,555 - turunan maksimum kedua dari penyimpangan.

Grafik dari proses kontrol di bagian terakhir dari penerbangan rudal balistik setelah optimasi ditunjukkan pada Gambar 13.

Gambar 13. Proses kontrol rudal balistik di kaki terakhir penerbangan.

Gambar 13 menunjukkan bahwa dengan pengaturan baru, penyimpangan dalam interval waktu penerbangan 40-66 detik tidak meningkat, berbeda dengan pengaturan yang dioptimalkan untuk segmen penerbangan kedua (lihat Gambar 12).

Jadi, kami mendapat pengaturan kontroler fuzzy untuk tiga bagian penerbangan. Mari kita buat sakelar mode yang akan mengalihkan pengaturan pengontrol selama penerbangan. Rangkaian sakelar mode ditunjukkan pada Gambar 14.


Gambar 14. Sakelar mode pengendali rudal balistik fuzzy.

Mode pengalihan akan berlangsung dalam waktu, di bagian atas, rangkaian logika sederhana membandingkan waktu model saat ini dengan titik pengalihan. Akibatnya, vektor kontrol dari tiga nilai dibentuk dalam multiplexer. Dalam vektor ini, nilai 1 berada pada posisi interval waktu saat ini.

Parameter dari kontroler fuzzy yang dihitung sebelumnya dengan metode optimisasi dikemas ke dalam vektor dari tiga nilai.

Dengan bantuan blok sampel dari tiga nilai, satu dipilih yang sesuai dengan 1 dalam vektor kontrol. Dengan demikian, ketika waktu berubah, parameter yang ditransfer ke pengontrol fuzzy berubah sesuai dengan bagian penerbangan saat ini.

Untuk kejelasan, nilai-nilai yang dikirimkan melalui jalur komunikasi ditampilkan dalam diagram. Angka tersebut sesuai dengan bagian terakhir dari penerbangan rudal balistik. Waktu lebih dari 40 detik. Vektor kontrol (0, 0, 1) parameter terakhir dari set dipasok ke controller.

Hasil simulasi mengendalikan sudut pitch roket dengan mengganti parameter regulator ditunjukkan pada Gambar 15.

Gambar 15a. Proses transisi.

Gambar 15b. Opsi kontrol.

Kesimpulan:
Kontroler yang didasarkan pada logika fuzzy dapat dikonfigurasi dengan metode optimisasi agar berfungsi dalam mode switching parameter.

Deviasi ketika bekerja dengan parameter variabel dalam contoh yang diberikan menurun 3-5 kali dibandingkan dengan operasi pengontrol dengan parameter konstan.

Arsip dengan proyek-proyek untuk studi independen dapat diunduh di sini ...