Inti umum penyortiran penyisipan adalah sebagai berikut:
- Iterasi elemen-elemen di bagian array yang tidak disortir.
- Setiap elemen dimasukkan ke dalam bagian array yang disortir di tempat yang seharusnya.
Ini, pada prinsipnya, adalah semua yang perlu Anda ketahui tentang penyortiran berdasarkan sisipan. Artinya, jenis penyisipan selalu membagi array menjadi 2 bagian - diurutkan dan tidak disortir. Item apa pun diambil dari bagian yang tidak disortir. Karena bagian lain dari array diurutkan, Anda dapat dengan cepat menemukan tempat Anda dalam array ini untuk elemen yang diekstraksi ini. Elemen disisipkan di mana diperlukan, sebagai akibatnya bagian yang disortir dari array meningkat, dan bagian yang tidak disortir berkurang. Itu saja. Semua jenis sisipan bekerja berdasarkan prinsip ini.
Titik terlemah dalam pendekatan ini adalah memasukkan elemen ke bagian array yang diurutkan. Sebenarnya, ini tidak mudah dan trik apa yang tidak harus Anda lakukan untuk menyelesaikan langkah ini.
Penyortiran penyisipan sederhana

Kami pergi melalui array dari kiri ke kanan dan memproses setiap elemen secara bergantian. Di sebelah kiri elemen berikutnya, kami meningkatkan bagian array yang diurutkan, ke kanan, saat proses berlangsung, bagian yang tidak disortir perlahan menguap. Di bagian array yang diurutkan, titik penyisipan untuk elemen berikutnya dicari. Elemen itu sendiri dikirim ke buffer, sebagai akibatnya sel kosong muncul dalam array - ini memungkinkan Anda untuk menggeser elemen dan membebaskan titik penyisipan.
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
Dengan menggunakan sisipan sederhana sebagai contoh, keuntungan utama sebagian besar (tetapi tidak semua!) Menyortir menurut sisipan terlihat nyata, yaitu, pemrosesan yang sangat cepat dari array yang hampir dipesan:

Dalam skenario ini, bahkan penerapan penyortiran sisipan paling primitif kemungkinan akan menyalip algoritma super-optimal untuk beberapa penyortiran cepat, termasuk pada array besar.
Ini difasilitasi oleh ide utama dari kelas ini - transfer elemen dari bagian array yang tidak disortir ke yang diurutkan. Dengan kedekatan data yang besarnya hampir sama, titik penyisipan biasanya terletak dekat dengan tepi bagian yang diurutkan, yang memungkinkan Anda untuk memasukkan dengan overhead yang paling sedikit.
Tidak ada yang lebih baik untuk menangani array yang hampir dipesan daripada menyortir penyisipan. Ketika Anda menemukan informasi di suatu tempat bahwa kompleksitas waktu terbaik untuk menyortir berdasarkan sisipan adalah
O ( n ) , maka kemungkinan besar Anda merujuk pada situasi dengan array yang hampir dipesan.
Urutkan berdasarkan sisipan pencarian biner sederhana

Karena tempat untuk disisipkan dicari di bagian array yang diurutkan, ide untuk menggunakan pencarian biner menunjukkan dirinya. Hal lain adalah bahwa pencarian untuk situs penyisipan tidak penting untuk kompleksitas waktu dari algoritma (pemakan sumber daya utama adalah tahap memasukkan elemen ke posisi yang ditemukan itu sendiri), oleh karena itu optimasi ini tidak banyak.
Dan dalam kasus array yang hampir diurutkan, pencarian biner dapat bekerja lebih lambat, karena dimulai dari tengah bagian yang diurutkan, yang, kemungkinan besar, akan terlalu jauh dari titik penyisipan (dan akan mengambil langkah lebih sedikit untuk melakukan pencarian normal dari posisi elemen ke titik penyisipan jika data dalam array secara keseluruhan dipesan).
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
Untuk mempertahankan pencarian biner, saya perhatikan bahwa ia dapat mengucapkan kata terakhir dalam efektivitas penyortiran lainnya dengan memasukkan. Berkat dia, khususnya, algoritma seperti pengurutan pustakawan dan pengurutan solitaire pergi ke kompleksitas waktu rata-rata
O ( n log n ) . Tapi tentang mereka nanti.
Penyortiran pasangan dengan sisipan sederhana
Modifikasi sisipan sederhana, dikembangkan di laboratorium rahasia Oracle Corporation. Penyortiran ini adalah bagian dari JDK, dan merupakan bagian dari Quicksort Dual-Pivot. Ini digunakan untuk mengurutkan array kecil (hingga 47 elemen) dan mengurutkan area kecil dari array besar.

Bukan hanya satu tapi dua elemen yang berdekatan dikirim ke buffer sekaligus. Pertama, elemen pasangan yang lebih besar dimasukkan, dan segera setelah itu, metode penyisipan sederhana diterapkan pada elemen pasangan yang lebih kecil.
Apa yang diberikannya? Tabungan untuk menangani barang yang lebih kecil dari pasangan. Baginya, pencarian untuk titik penyisipan dan penyisipan itu sendiri dilakukan hanya pada bagian yang diurutkan dari array, yang tidak termasuk area yang diurutkan yang digunakan untuk memproses elemen yang lebih besar dari pasangan. Ini menjadi mungkin karena elemen yang lebih besar dan lebih kecil diproses segera satu demi satu dalam satu lintasan loop luar.
Ini tidak memengaruhi kompleksitas waktu rata-rata (masih tetap sama dengan
O ( n 2 )), namun demikian, pemasangan berpasangan bekerja sedikit lebih cepat daripada yang biasa.
Saya menggambarkan algoritma dalam Python, tetapi di sini saya memberikan sumber asli (dimodifikasi untuk dibaca) di Jawa:
for (int k = left; ++left <= right; k = ++left) {
Sortir Shell

Algoritma ini memiliki pendekatan yang sangat cerdas dalam menentukan bagian array yang dianggap diurutkan. Dalam sisipan sederhana, semuanya sederhana: dari elemen saat ini, semua yang di sebelah kiri sudah diurutkan, semua yang di sebelah kanan belum diurutkan. Tidak seperti sisipan sederhana, pengurutan Shell tidak mencoba untuk segera membentuk bagian yang diurutkan secara ketat dari array di sebelah kiri elemen. Ini menciptakan bagian array yang
hampir disortir di sebelah kiri elemen dan melakukannya dengan cukup cepat.
Penyortiran shell melemparkan elemen saat ini ke buffer dan membandingkannya dengan sisi kiri array. Jika menemukan elemen yang lebih besar di sebelah kiri, itu menggesernya ke kanan, memberikan ruang untuk penyisipan. Tetapi pada saat yang sama, itu tidak mengambil seluruh bagian kiri, tetapi hanya sekelompok elemen tertentu darinya, di mana elemen-elemen tersebut berjarak satu sama lain dengan jarak tertentu. Sistem seperti ini memungkinkan Anda untuk dengan cepat memasukkan elemen ke sekitar area array di mana mereka seharusnya berada.
Dengan setiap iterasi loop utama, jarak ini berangsur-angsur berkurang dan ketika menjadi sama dengan satu, maka Shell sortir pada saat ini berubah menjadi sortir klasik dengan sisipan sederhana, yang diberikan pada pemrosesan array yang hampir diurutkan. Penyortiran array yang hampir diurutkan menyisipkan konversi yang sepenuhnya terurut dengan cepat.
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
Penyortiran sisir dengan prinsip yang sama meningkatkan penyortiran gelembung, sehingga kompleksitas waktu dari algoritma dengan
O ( n 2 ) melonjak hingga
O ( n log n ) . Sayangnya, Shell tidak berhasil mengulangi prestasi ini - kompleksitas waktu terbaik mencapai
O ( n log 2 n ) .
Beberapa habrastati telah ditulis tentang penyortiran Shell, jadi kami tidak akan kelebihan informasi dan melanjutkan.
Penyortiran pohon
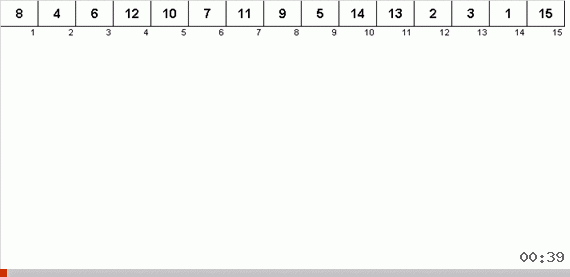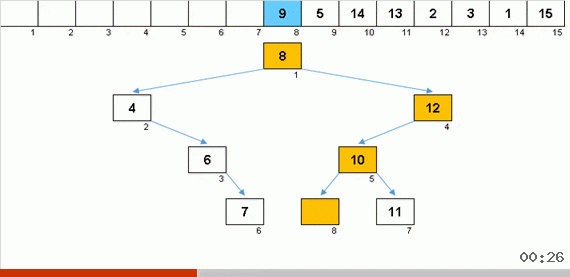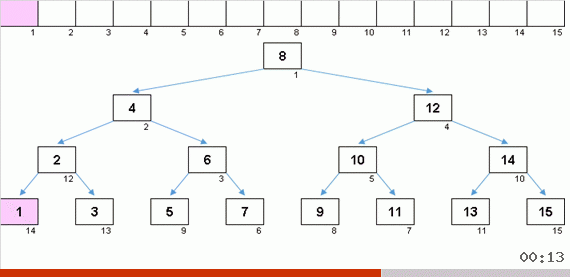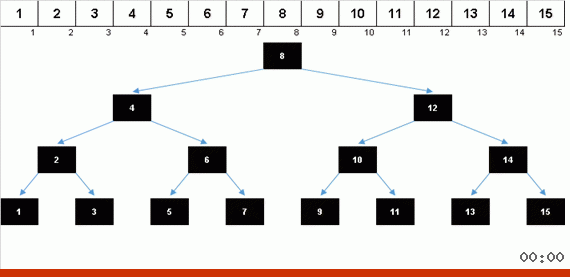
Menyortir dengan pohon karena memori tambahan dengan cepat menyelesaikan masalah menambahkan elemen lain ke bagian array yang diurutkan. Selain itu, pohon biner bertindak sebagai bagian yang diurutkan dari array. Sebuah pohon terbentuk secara harfiah saat terbang di atas elemen.
Elemen dibandingkan pertama dengan root, dan kemudian dengan lebih banyak node bersarang sesuai dengan prinsip: jika elemen lebih kecil dari node, maka kita turun cabang kiri, jika tidak kurang, maka yang benar. Sebuah pohon yang dibangun dengan aturan seperti itu kemudian dapat dengan mudah dielakkan untuk berpindah dari node dengan nilai lebih rendah ke node dengan nilai lebih besar (dan dengan demikian mendapatkan semua elemen dalam urutan yang meningkat).
Hambatan utama pengurutan menurut sisipan (biaya memasukkan elemen ke tempatnya di bagian array yang diurutkan) diselesaikan di sini, konstruksi berlangsung cukup cepat. Dalam kasus apa pun, untuk membebaskan titik penyisipan, tidak perlu secara perlahan memindahkan karavan elemen seperti pada algoritma sebelumnya. Tampaknya ini dia, yang terbaik dari menyortir sisipan. Tapi ada masalah.
Ketika Anda mendapatkan pohon Natal simetris yang indah (yang disebut pohon seimbang sempurna) seperti pada animasi tiga paragraf di atas, penyisipan terjadi dengan cepat, karena pohon dalam kasus ini memiliki tingkat bersarang serendah mungkin. Tetapi struktur seimbang (atau paling tidak dekat dengan itu) dari array acak jarang diperoleh. Dan pohon itu, kemungkinan besar, akan menjadi tidak sempurna dan tidak seimbang - dengan distorsi, cakrawala yang berserakan dan jumlah level yang berlebihan.
Array acak dengan nilai dari 1 hingga 10. Elemen dalam urutan ini menghasilkan pohon biner yang tidak seimbang: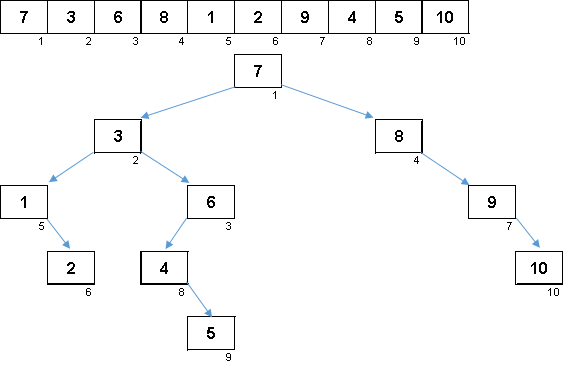
Sebatang pohon tidak cukup untuk dibangun, masih perlu dielakkan. Semakin banyak ketidakseimbangan - semakin kuat algoritma traversal pohon akan terpeleset. Di sini, seperti kata bintang-bintang, array acak dapat menghasilkan hambatan jelek (yang lebih mungkin) dan fraktal seperti pohon.
Nilai elemen-elemennya sama, tetapi urutannya berbeda. Pohon biner seimbang dihasilkan: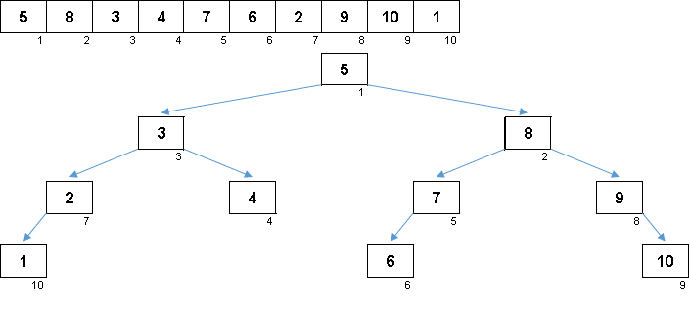
 Di sakura yang indah
Di sakura yang indah
Kelopak tidak cukup:
Pohon lusinan biner.Masalah pohon tidak seimbang diselesaikan dengan penyortiran inversi, yang menggunakan jenis khusus pohon pencarian biner - pohon hamparan. Ini adalah pohon transformator yang luar biasa, yang setelah setiap operasi dibangun kembali dalam keadaan seimbang. Tentang itu akan menjadi artikel tersendiri. Pada saat itu saya akan menyiapkan implementasi Python untuk Tree Sort dan Splay sort.
Baiklah, baiklah, kami sebentar menyortir menyortir yang paling populer. Sisipan sederhana, cangkang dan pohon biner yang kita semua tahu dari sekolah. Sekarang pertimbangkan perwakilan lain dari kelas ini, yang tidak begitu dikenal luas.
Wiki / Wiki -
Penyisipan , Shell / Shell , Pohon / PohonArtikel Seri:
Siapa yang menggunakan AlgoLab - Saya sarankan memperbarui file. Saya menambahkan sisipan pencarian biner sederhana dan sisipan berpasangan ke aplikasi ini. Dia juga sepenuhnya menulis ulang visualisasi untuk Shell (dalam versi sebelumnya tidak ada sesuatu untuk dipahami) dan menambahkan sorotan ke cabang induk ketika memasukkan elemen ke pohon biner.