Jaringan saraf telah merevolusi bidang pengenalan pola, tetapi karena interpretabilitas yang tidak jelas dari prinsip operasi, mereka tidak digunakan di bidang-bidang seperti kedokteran dan penilaian risiko. Ini membutuhkan representasi visual dari jaringan, yang akan membuatnya bukan kotak hitam, tetapi setidaknya "tembus".
Cristopher Olah, dalam Neural Networks, Manifolds, dan Topology, mendemonstrasikan prinsip-prinsip operasi jaringan saraf dan menghubungkannya dengan teori matematika tentang topologi dan keanekaragaman, yang berfungsi sebagai dasar untuk artikel ini. Untuk menunjukkan operasi jaringan saraf, digunakan jaringan saraf dalam dimensi rendah.
Memahami perilaku jaringan saraf yang dalam umumnya bukan tugas yang sepele. Lebih mudah untuk mengeksplorasi jaringan saraf dalam dimensi rendah - jaringan di mana hanya ada beberapa neuron di setiap lapisan. Untuk jaringan dimensi rendah, Anda dapat membuat visualisasi untuk memahami perilaku dan pelatihan jaringan tersebut. Perspektif ini akan memberikan pemahaman yang lebih dalam tentang perilaku jaringan saraf dan mengamati koneksi yang menggabungkan jaringan saraf dengan bidang matematika yang disebut topologi.
Sejumlah hal menarik mengikuti dari ini, termasuk batas bawah fundamental pada kompleksitas jaringan saraf yang mampu mengklasifikasikan set data tertentu.
Pertimbangkan prinsip jaringan menggunakan contoh
Mari kita mulai dengan kumpulan data sederhana - dua kurva di pesawat. Tugas jaringan akan belajar untuk mengklasifikasikan titik-titik milik kurva.
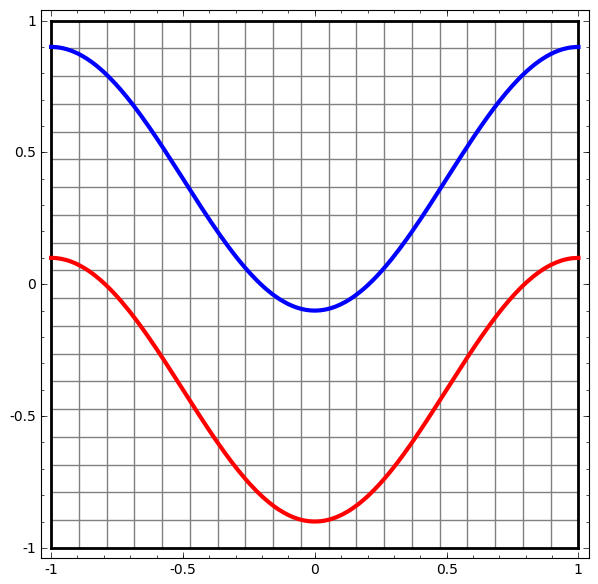
Cara yang jelas untuk memvisualisasikan perilaku jaringan saraf, untuk melihat bagaimana algoritma mengklasifikasikan semua objek yang mungkin (dalam contoh kami, poin) dari kumpulan data.
Mari kita mulai dengan kelas jaringan saraf yang paling sederhana, dengan satu lapisan input dan output. Jaringan semacam itu mencoba memisahkan dua kelas data dengan membaginya dengan satu baris.
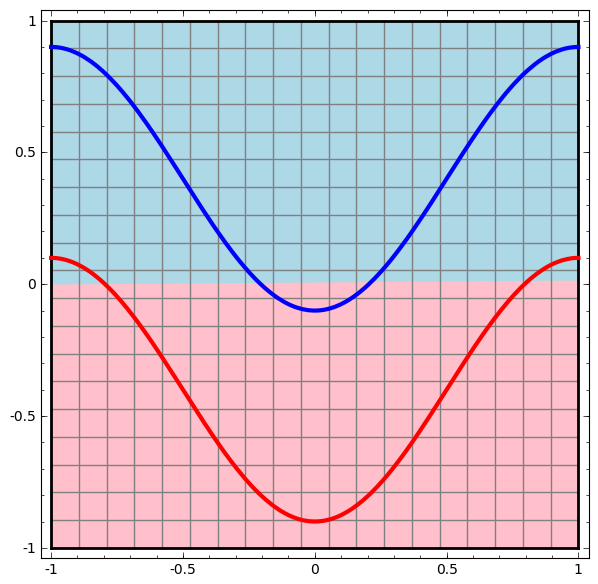
Jaringan seperti itu tidak digunakan dalam praktik. Jaringan saraf modern biasanya memiliki beberapa lapisan antara input dan output mereka, yang disebut lapisan "tersembunyi".
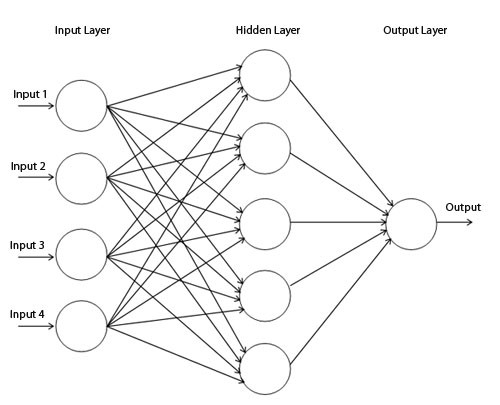
Diagram jaringan sederhana
Kami memvisualisasikan perilaku jaringan ini, mengamati apa yang dilakukannya dengan titik yang berbeda di bidangnya. Jaringan lapisan tersembunyi memisahkan data dari kurva yang lebih kompleks daripada garis.
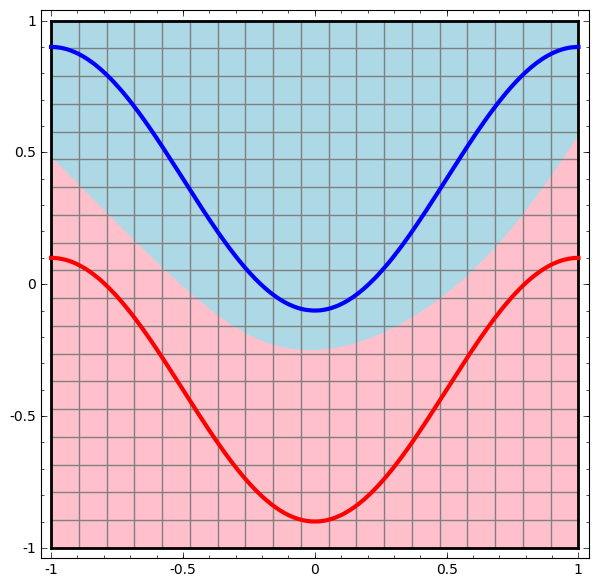
Dengan setiap lapisan, jaringan mengubah data, menciptakan tampilan baru. Kita dapat melihat data di setiap tampilan ini dan bagaimana jaringan dengan lapisan tersembunyi mengklasifikasikannya. Ketika algoritma mencapai presentasi akhir, jaringan saraf akan menarik garis melalui data (atau dalam dimensi yang lebih tinggi - hyperplane).
Dalam visualisasi sebelumnya, data dalam tampilan mentah dipertimbangkan. Anda dapat membayangkan ini dengan melihat pada layer input. Sekarang, pertimbangkan setelah dikonversi ke lapisan pertama. Anda dapat membayangkan ini dengan melihat lapisan yang tersembunyi.
Setiap pengukuran berhubungan dengan aktivasi neuron pada lapisan.
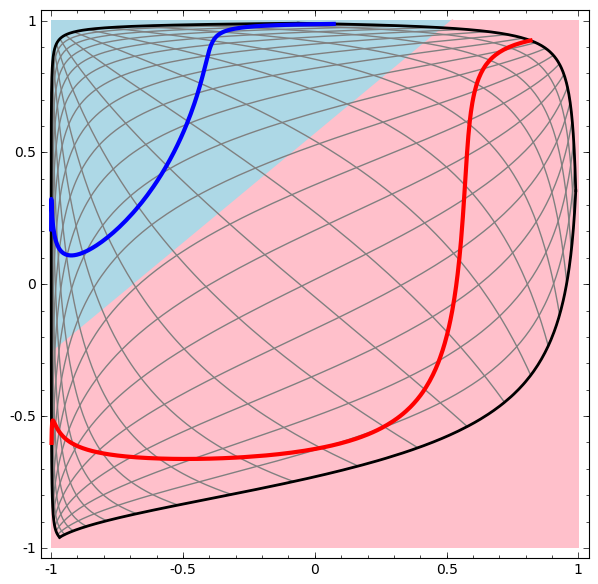
Lapisan tersembunyi dilatih pada tampilan sehingga data dapat dipisahkan secara linear.
Render lapisan berkelanjutanDalam pendekatan yang dijelaskan pada bagian sebelumnya, kita belajar untuk memahami jaringan dengan melihat presentasi yang sesuai dengan setiap lapisan. Ini memberi kita daftar pandangan tersendiri.
Bagian yang tidak sepele adalah memahami bagaimana kita berpindah dari satu ke yang lain. Untungnya, level jaringan saraf memiliki properti yang memungkinkan hal ini.
Ada banyak jenis lapisan yang digunakan dalam jaringan saraf.
Pertimbangkan layer tanh untuk contoh spesifik. Tanh-tanh-layer (Wx + b) terdiri dari:
- Transformasi linear dari matriks "berat" W
- Penerjemahan menggunakan vektor b
- Aplikasi tempat tanh.
Kami dapat mewakili ini sebagai transformasi berkelanjutan sebagai berikut:
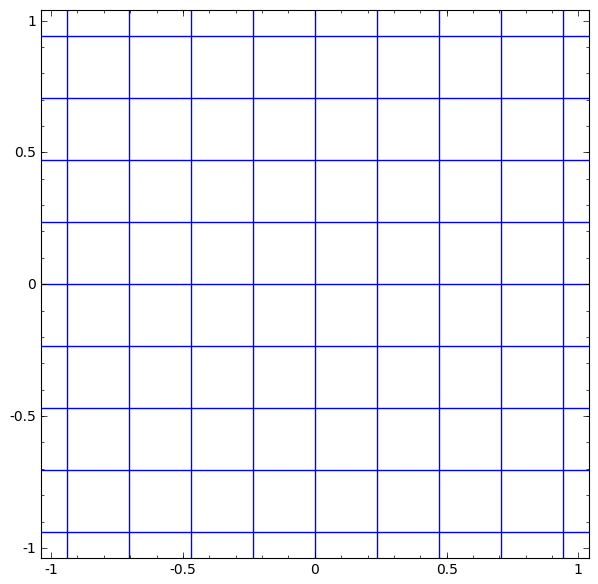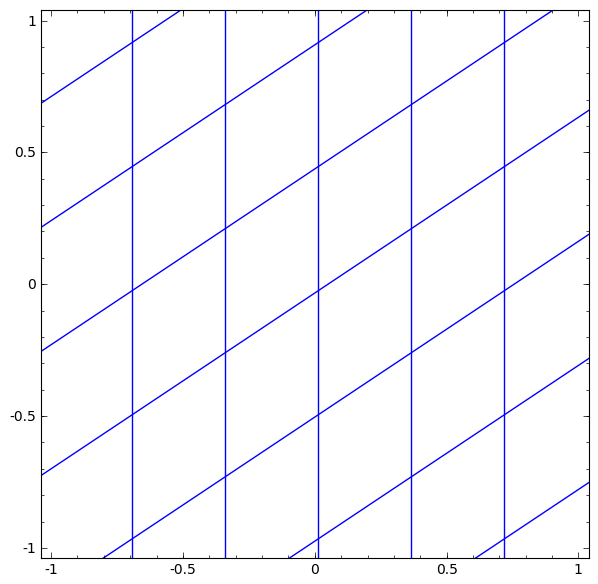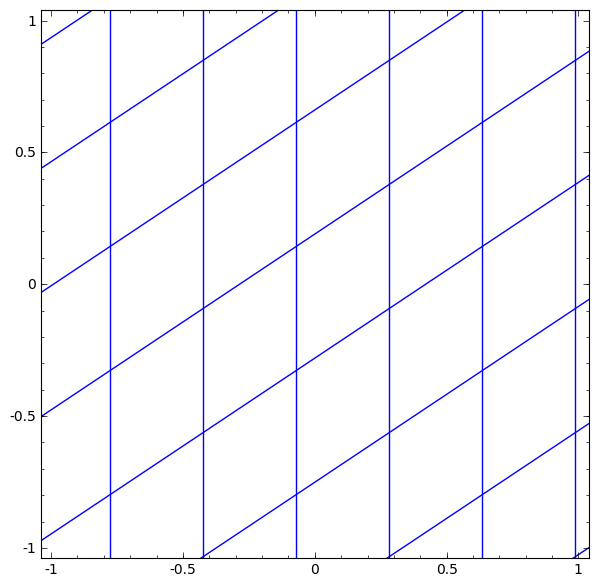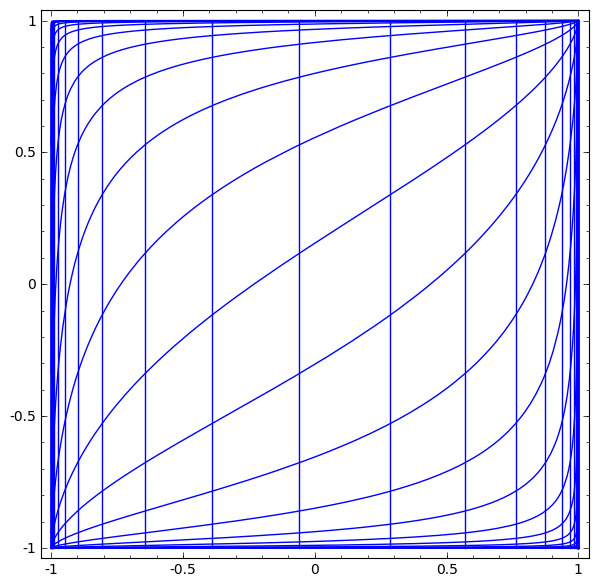
Prinsip operasi ini sangat mirip dengan lapisan standar lainnya yang terdiri dari transformasi affine, diikuti oleh penerapan fungsi aktivasi monotonik secara langsung.
Metode ini dapat digunakan untuk memahami jaringan yang lebih kompleks. Jadi, jaringan berikut mengklasifikasikan dua spiral yang sedikit kusut menggunakan empat lapisan tersembunyi. Seiring waktu, dapat dilihat bahwa jaringan saraf bergerak dari pandangan mentah ke tingkat yang lebih tinggi yang dipelajari jaringan untuk mengklasifikasikan data. Sementara spiral awalnya kusut, menjelang akhir mereka terpisah secara linear.
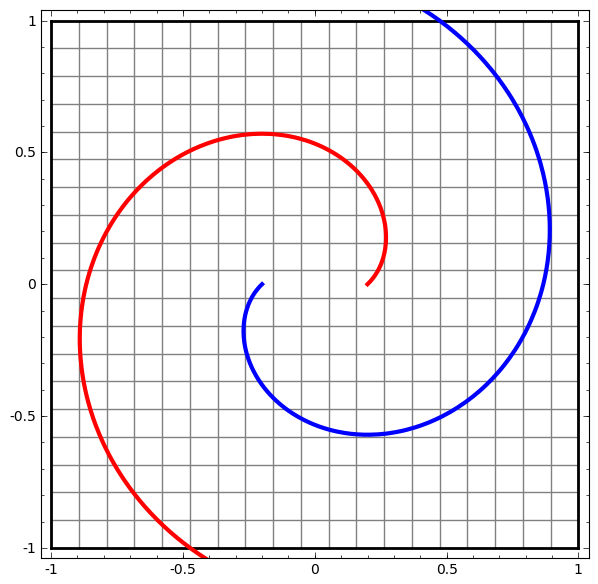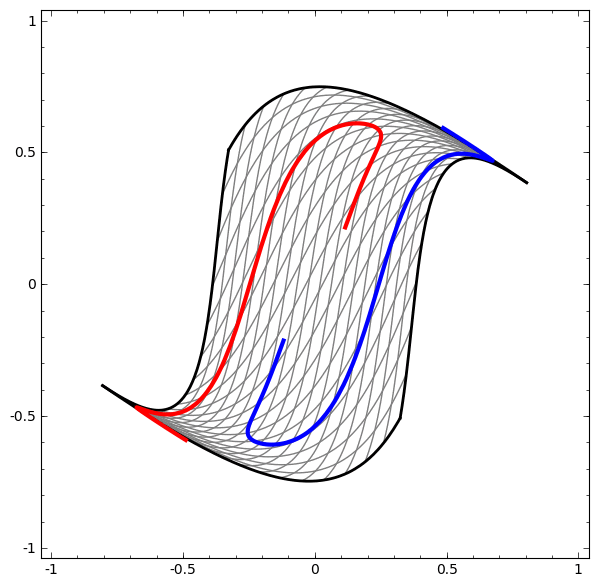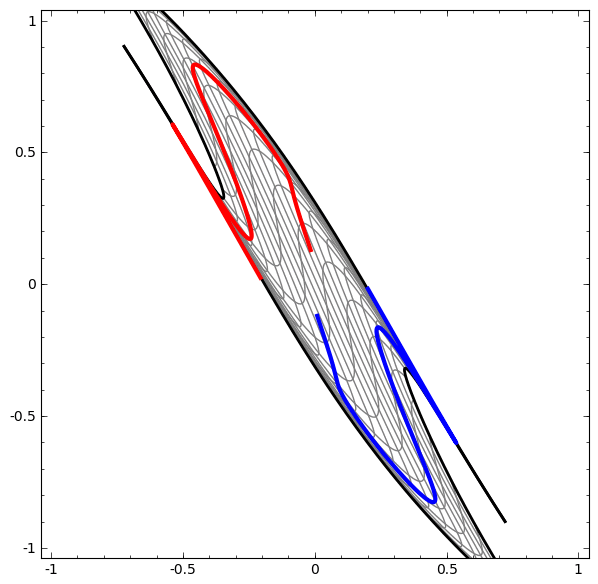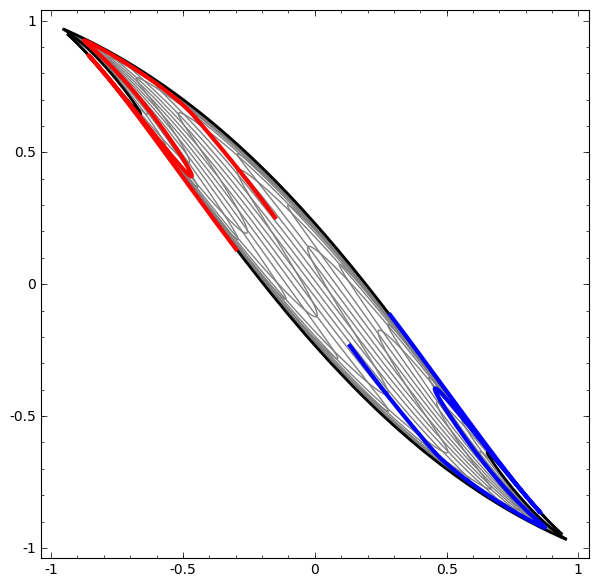
Di sisi lain, jaringan berikutnya, yang juga menggunakan beberapa level, tetapi tidak dapat mengklasifikasikan dua spiral, yang lebih kusut.
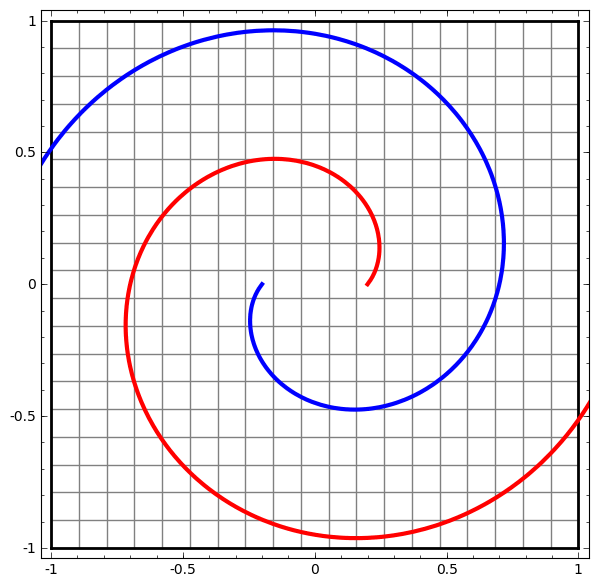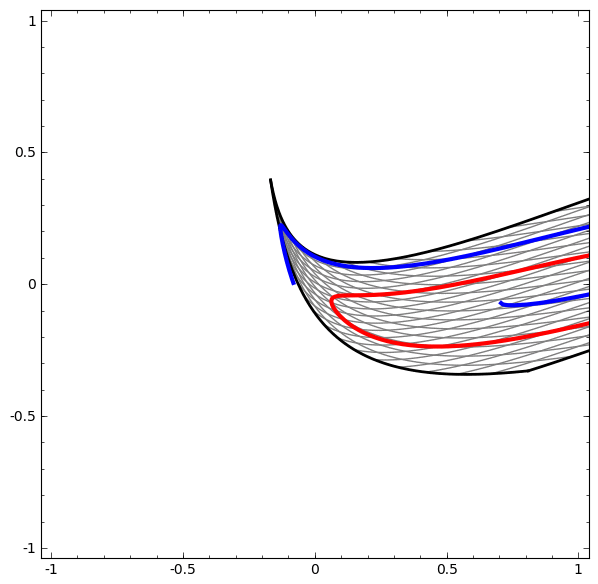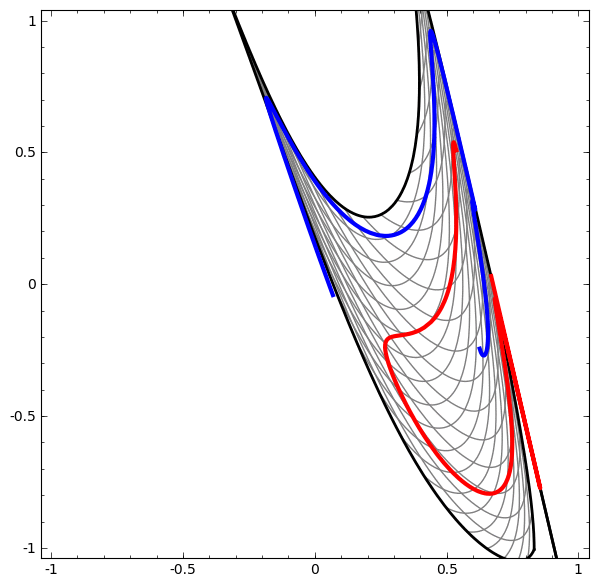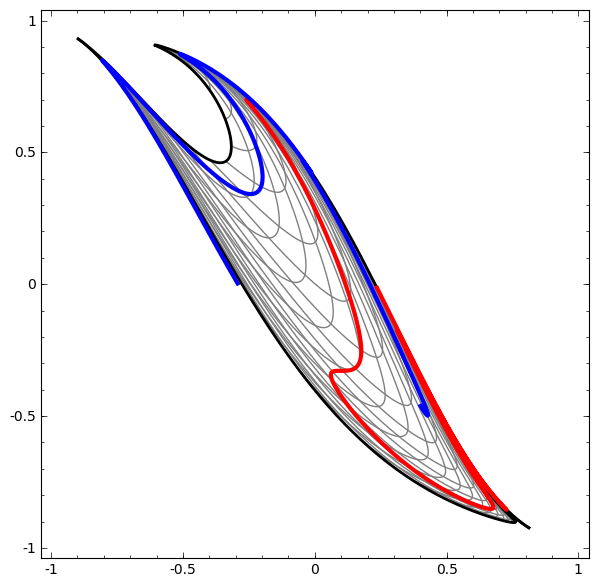
Perlu dicatat bahwa tugas-tugas ini memiliki kompleksitas terbatas, karena jaringan saraf dimensi rendah digunakan. Jika jaringan yang lebih luas digunakan, pemecahan masalah disederhanakan.
Layers Tang
Setiap lapisan meregangkan dan menekan ruang, tetapi tidak pernah memotong, tidak pecah, dan tidak melipatnya. Secara intuitif, kita melihat bahwa sifat topologis dipertahankan pada setiap lapisan.
Transformasi semacam itu yang tidak mempengaruhi topologi disebut homomorfisma (Wiki - Ini adalah pemetaan sistem aljabar A yang mempertahankan operasi dasar dan hubungan dasar). Secara formal, mereka adalah bijections yang merupakan fungsi kontinu di kedua arah. Dalam pemetaan bijective, setiap elemen dari satu set berkorespondensi dengan tepat satu elemen dari set lainnya, dan pemetaan invers yang memiliki properti yang sama didefinisikan.
TeoremaLapisan dengan input N dan output N adalah homomorfisme jika matriks bobot W tidak mengalami degenerasi. (Anda harus berhati-hati tentang domain dan jangkauan.)
Bukti:1. Asumsikan bahwa W memiliki determinan bukan-nol. Maka itu adalah fungsi linier bijective dengan invers linier. Fungsi linear kontinu. Jadi, perkalian dengan W adalah homeomorfisme.
2. Pemetaan - homomorfisme
3. tanh (baik sigmoid dan softplus, tetapi bukan ReLU) adalah fungsi kontinu dengan invers kontinu. Mereka adalah bijections jika kita berhati-hati tentang area dan jangkauan yang kita pertimbangkan. Penggunaannya secara langsung adalah homomorfisme.
Jadi, jika W memiliki determinan bukan-nol, seratnya adalah homeomorfik.
Topologi dan klasifikasi
Pertimbangkan kumpulan data dua dimensi dengan dua kelas A, B⊂R2:
A = {x | d (x, 0) <1/3}
B = {x | 2/3 <d (x, 0) <1}

Merah, B biru
Persyaratan: Jaringan saraf tidak dapat mengklasifikasikan dataset ini tanpa 3 atau lebih lapisan tersembunyi, berapa pun lebarnya.
Seperti disebutkan sebelumnya, klasifikasi dengan fungsi sigmoid atau lapisan softmax setara dengan mencoba menemukan hyperplane (atau dalam hal ini garis) yang memisahkan A dan B dalam representasi akhir. Dengan hanya dua lapisan tersembunyi, jaringan secara topologi tidak dapat berbagi data dengan cara ini, dan akan mengalami kegagalan dalam kumpulan data ini.
Dalam visualisasi berikutnya, kami mengamati tampilan laten saat jaringan berlatih bersama dengan garis klasifikasi.
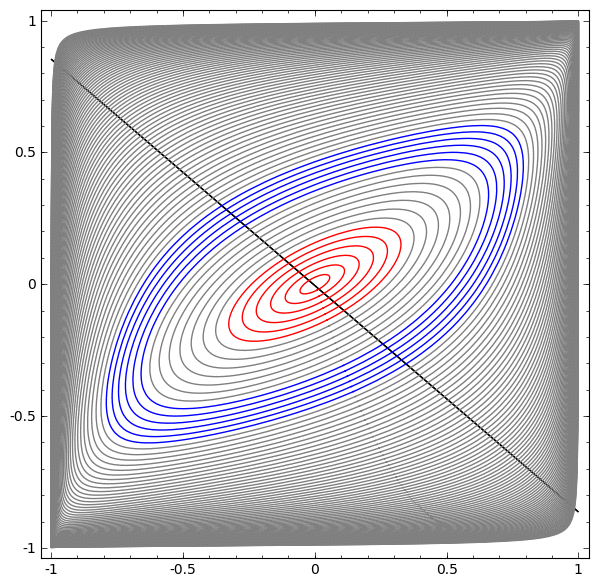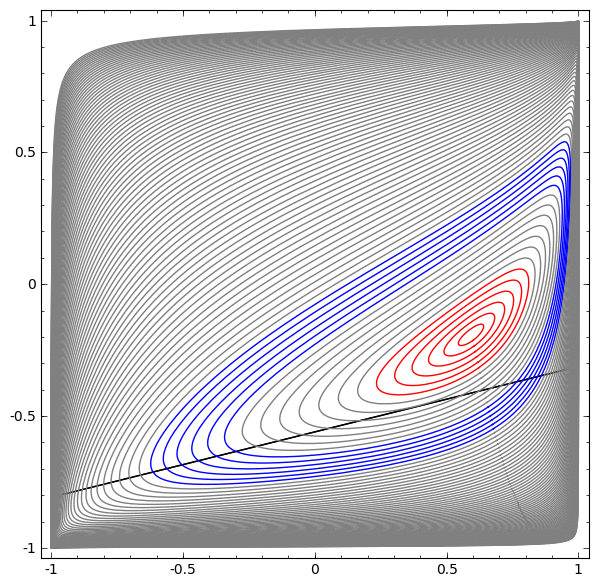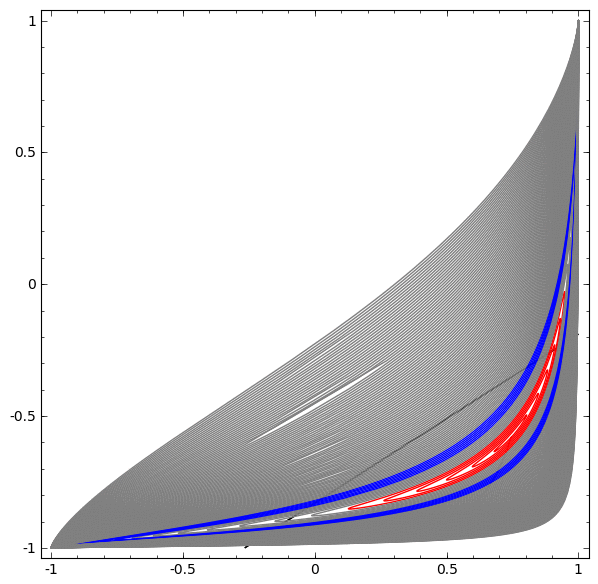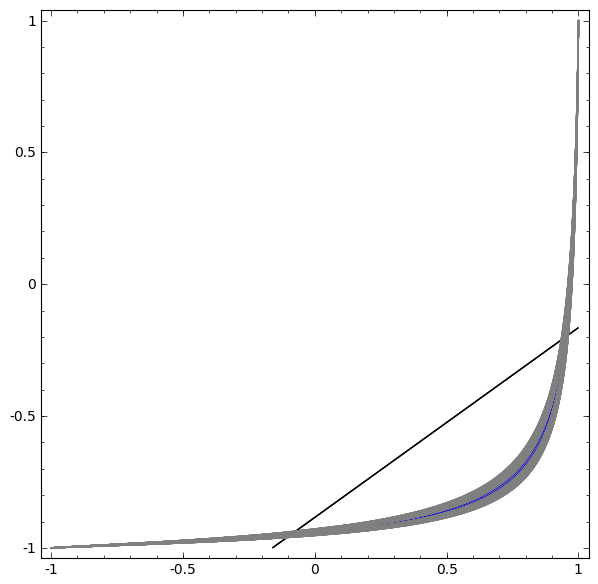
Untuk jaringan pelatihan ini tidak cukup untuk mencapai hasil seratus persen.
Algoritma jatuh ke minimum lokal non-produktif, tetapi mampu mencapai ~ 80% akurasi klasifikasi.
Dalam contoh ini, hanya ada satu lapisan tersembunyi, tetapi tidak berhasil.
Pernyataan Entah setiap lapisan adalah homomorfisme, atau matriks bobot dari lapisan memiliki determinan 0.
Bukti:Jika ini adalah homomorfisme, maka A masih dikelilingi oleh B, dan garis tidak dapat memisahkan mereka. Tapi anggap itu memiliki penentu 0: maka kumpulan data runtuh pada beberapa sumbu. Karena kita berhadapan dengan sesuatu yang homeomorfik dengan dataset asli, A dikelilingi oleh B, dan runtuh pada sumbu apa pun berarti bahwa kita akan memiliki beberapa titik dari campuran A dan B, dan ini membuatnya tidak mungkin untuk dibedakan.
Jika kita menambahkan elemen tersembunyi ketiga, masalahnya akan menjadi sepele. Jaringan saraf mengenali representasi berikut:
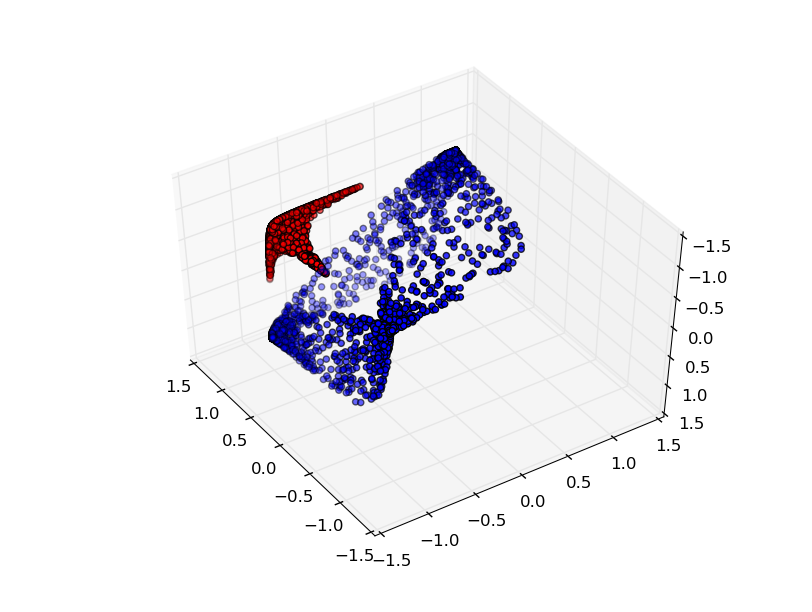
Tampilan memungkinkan untuk memisahkan dataset dengan hyperplane.
Untuk lebih memahami apa yang sedang terjadi, mari kita lihat pada kumpulan data yang lebih sederhana, yaitu satu dimensi:

A = [- 1 / 3,1 / 3]
B = [- 1, −2 / 3] ∪ [2 / 3,1]
Tanpa menggunakan lapisan dua atau lebih elemen tersembunyi, kami tidak dapat mengklasifikasikan dataset ini. Tetapi, jika kita menggunakan jaringan dengan dua elemen, kita akan belajar bagaimana merepresentasikan data sebagai kurva yang baik yang memungkinkan kita untuk memisahkan kelas menggunakan garis:
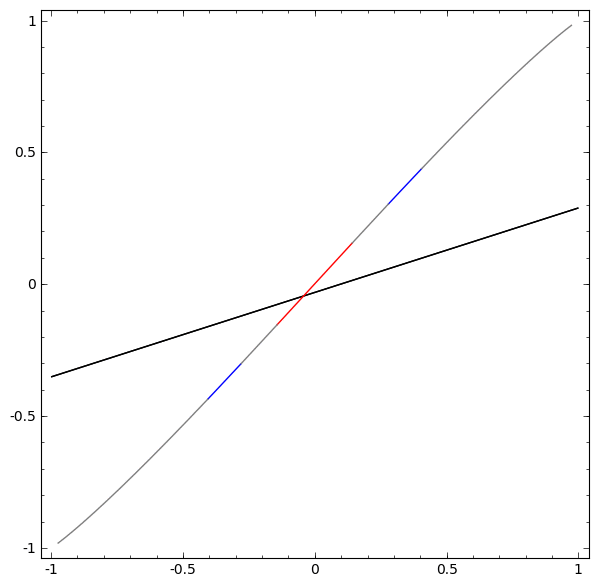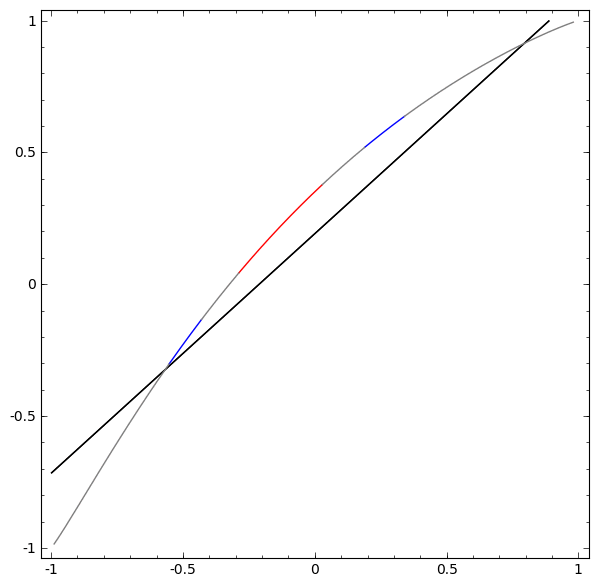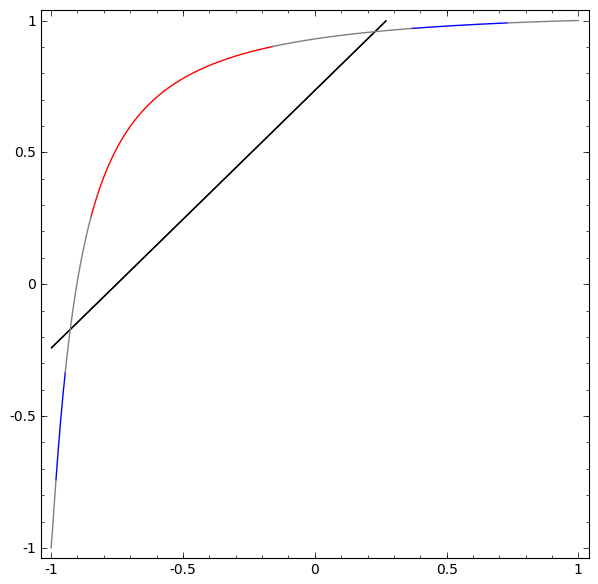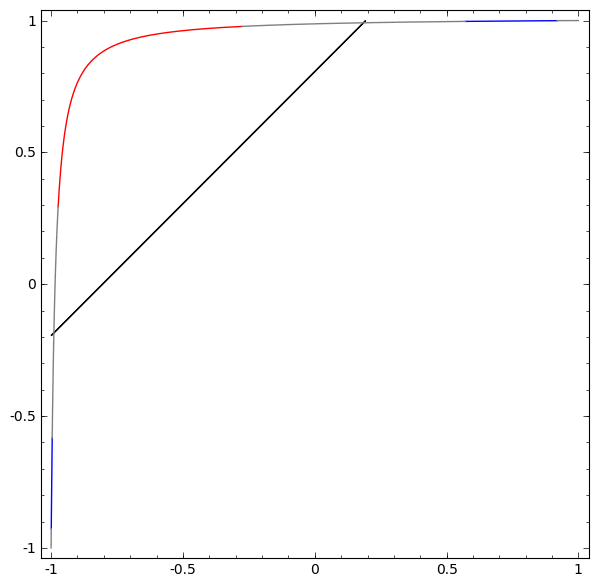
Apa yang sedang terjadi Satu elemen tersembunyi belajar menembak ketika x> -1/2, dan satu elemen belajar menembak ketika x> 1/2. Ketika yang pertama dipicu, tetapi bukan yang kedua, kita tahu bahwa kita berada di A.
Berbagai dugaan
Apakah ini berlaku untuk kumpulan data dari dunia nyata, seperti kumpulan gambar? Jika Anda serius tentang hipotesis keragaman, saya pikir itu penting.
Hipotesis multidimensi adalah bahwa data alami membentuk manifold dimensi rendah di ruang implantasi. Ada alasan teoretis [1] dan eksperimental [2] untuk percaya bahwa ini benar. Jika demikian, maka tugas algoritma klasifikasi adalah untuk memisahkan bundel manifold terjerat.
Dalam contoh sebelumnya, satu kelas benar-benar mengelilingi yang lain. Namun, tidak mungkin bahwa berbagai gambar anjing benar-benar dikelilingi oleh koleksi gambar kucing. Tetapi ada situasi topologis lain yang lebih masuk akal yang mungkin masih muncul, seperti yang akan kita lihat di bagian selanjutnya.
Koneksi dan homotopies
Dataset menarik lainnya adalah dua terhubung tori A dan B.

Seperti kumpulan data sebelumnya yang kami kaji, kumpulan data ini tidak dapat dibagi tanpa menggunakan n +1 dimensi, yaitu dimensi keempat.
Koneksi dipelajari dalam teori simpul, di bidang topologi. Kadang-kadang, ketika kita melihat koneksi, tidak segera jelas apakah itu inkoherensi (banyak hal yang kusut tetapi dapat dipisahkan oleh deformasi terus-menerus) atau tidak.
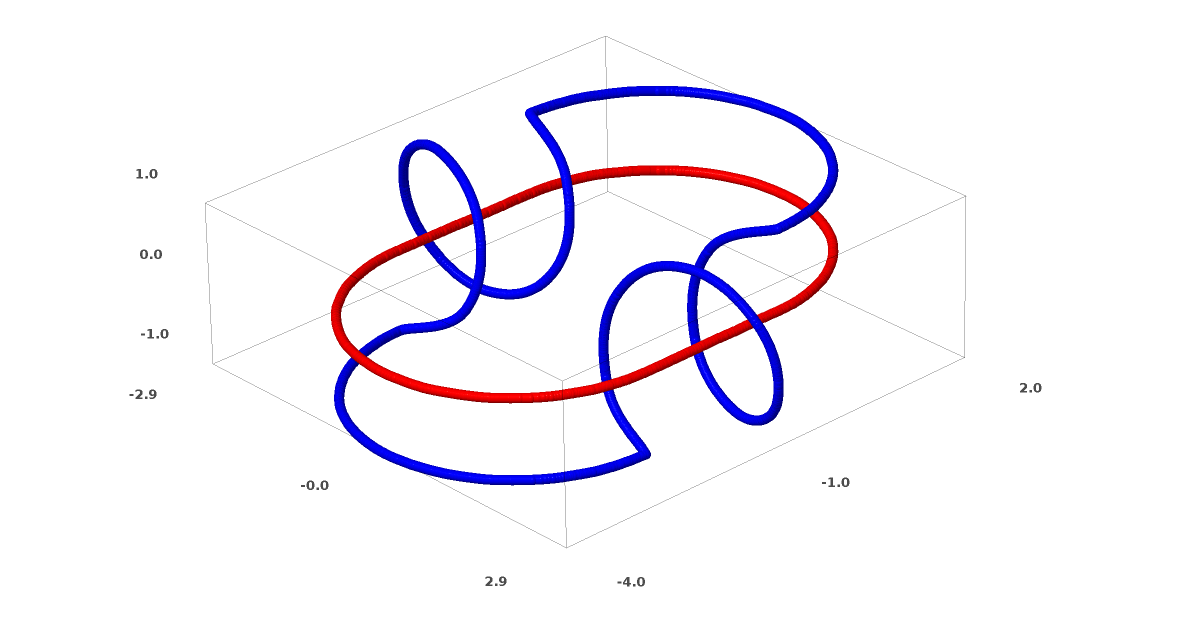
Inkoherensi yang relatif sederhana.
Jika jaringan saraf menggunakan lapisan dengan hanya tiga unit dapat mengklasifikasikannya, maka itu tidak koheren. (Pertanyaan: Dapatkah semua inkoherensi diklasifikasikan melalui jaringan hanya dengan tiga inkoherensi, secara teoritis?)
Dari sudut pandang node ini, visualisasi kontinu dari representasi yang dibuat oleh jaringan saraf adalah prosedur untuk mengurai koneksi. Dalam topologi, kita akan menyebut isotop ambient ini antara tautan asli dan yang dipisahkan.
Secara formal, isotop ruang sekitar antara varietas A dan B adalah fungsi kontinu F: [0,1] × X → Y sedemikian sehingga setiap Ft adalah homeomorfisme dari X hingga jangkauannya, F0 adalah fungsi identitas, dan F1 memetakan fungsi menjadi B. T .e. Ft terus berpindah dari peta A ke dirinya sendiri, ke peta A ke B.
Teorema: ada isotop ruang sekitar antara pintu masuk dan representasi tingkat jaringan jika: a) W tidak merosot, b) kami siap mentransfer neuron ke lapisan tersembunyi dan c) ada lebih dari 1 elemen tersembunyi.
Bukti:1. Bagian tersulit adalah transformasi linear. Untuk memungkinkan ini, kita perlu W untuk memiliki penentu positif. Premis kami adalah bahwa itu tidak sama dengan nol, dan kami dapat membalikkan tanda jika negatif dengan mengganti dua neuron yang tersembunyi, dan oleh karena itu kami dapat menjamin bahwa determinannya positif. Ruang matriks determinan positif terhubung, oleh karena itu terdapat p: [0,1] → GLn ®5 sedemikian sehingga p (0) = Id dan p (1) = W. Kita dapat terus berpindah dari fungsi identitas ke transformasi W menggunakan fungsi x → p (t) x, mengalikan x pada setiap titik waktu t dengan p (t) matriks yang terus-menerus lewat.
2. Kita dapat terus berpindah dari fungsi identitas ke b-peta menggunakan fungsi x → x + tb.
3. Kita dapat terus berpindah dari fungsi yang identik ke penggunaan σ dengan fungsi: x → (1-t) x + tσ (x)
Sampai sekarang, hubungan yang kita bicarakan tidak mungkin muncul dalam data nyata, tetapi ada generalisasi tingkat yang lebih tinggi. Adalah masuk akal bahwa fitur-fitur seperti itu mungkin ada dalam data nyata.
Koneksi dan node adalah manifold satu dimensi, tetapi kita membutuhkan 4 dimensi sehingga jaringan dapat menguraikan semuanya. Demikian pula, ruang dimensi yang lebih tinggi mungkin diperlukan untuk dapat memperluas manifold n-dimensi. Semua manifold n-dimensional dapat diperluas dalam 2n + 2 dimensi. [3]
Mudah keluar
Cara mudah adalah mencoba menarik manifold terpisah dan meregangkan bagian-bagian yang kusut mungkin. Meskipun ini tidak akan dekat dengan solusi asli, solusi seperti itu dapat mencapai akurasi klasifikasi yang relatif tinggi dan menjadi minimum lokal yang dapat diterima.

Minima lokal seperti itu sama sekali tidak berguna dalam hal mencoba memecahkan masalah topologi, tetapi masalah topologi dapat memberikan motivasi yang baik untuk mempelajari masalah ini.
Di sisi lain, jika kita hanya tertarik untuk mencapai hasil klasifikasi yang baik, pendekatannya dapat diterima. Jika sedikit manifold data tertangkap pada manifold lain, apakah ini masalah? Sangat mungkin bahwa akan dimungkinkan untuk memperoleh hasil klasifikasi yang baik secara sewenang-wenang, terlepas dari masalah ini.
Lapisan yang ditingkatkan untuk memanipulasi manifold?
Sulit membayangkan bahwa lapisan standar dengan transformasi affine benar-benar bagus untuk memanipulasi manifold.
Mungkin masuk akal untuk memiliki lapisan yang sama sekali berbeda, yang dapat kita gunakan dalam komposisi dengan yang lebih tradisional?
Studi tentang bidang vektor dengan arah di mana kami ingin menggeser manifold cukup menjanjikan:

Dan kemudian kita merusak ruang berdasarkan bidang vektor:
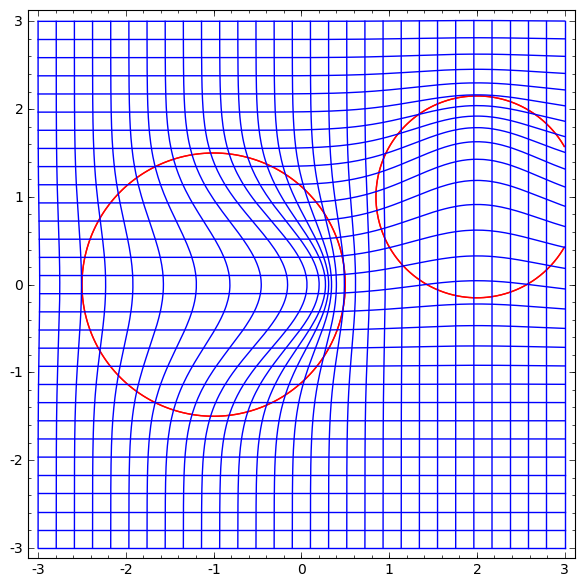
Seseorang dapat mempelajari bidang vektor pada titik-titik tetap (hanya mengambil beberapa titik tetap dari data uji yang ditetapkan untuk digunakan sebagai jangkar) dan menginterpolasi entah bagaimana.
Bidang vektor di atas memiliki bentuk:P (x) = (v0f0 (x) + v1f1 (x)) / (1 + 0 (x) + f1 (x))
Di mana v0 dan v1 adalah vektor, dan f0 (x) dan f1 (x) adalah n-dimensi Gaussians.
Lapisan Tetangga K-Terdekat
Keterpisahan linear dapat menjadi kebutuhan besar dan mungkin tidak masuk akal untuk jaringan saraf. Wajar untuk menggunakan metode k-tetangga terdekat (k-NN). Namun, keberhasilan k-NN sangat tergantung pada presentasi yang diklasifikasi, sehingga presentasi yang baik diperlukan sebelum k-NN dapat bekerja dengan baik.
k-NN dapat dibedakan sehubungan dengan representasi di mana ia bertindak. Dengan cara ini, kita bisa langsung melatih jaringan untuk mengklasifikasikan k-NN. Ini dapat dilihat sebagai semacam lapisan "tetangga terdekat" yang bertindak sebagai alternatif untuk softmax.
Kami tidak ingin memperingatkan dengan seluruh rangkaian pelatihan kami untuk setiap pesta kecil, karena itu akan menjadi prosedur yang sangat mahal. Pendekatan yang diadaptasi adalah untuk mengklasifikasikan setiap elemen dari mini-lot berdasarkan kelas dari elemen-elemen lain dari mini-lot, memberikan masing-masing berat unit dibagi dengan jarak dari target klasifikasi.
Sayangnya, bahkan dengan arsitektur yang kompleks, menggunakan k-NN mengurangi kemungkinan kesalahan - dan menggunakan arsitektur yang lebih sederhana menurunkan hasilnya.
Kesimpulan
Properti topologi data, seperti hubungan, dapat membuat pembagian linear kelas tidak mungkin menggunakan jaringan dimensi rendah, terlepas dari kedalamannya. Bahkan dalam kasus di mana secara teknis dimungkinkan. Misalnya, spiral, yang sangat sulit untuk dipisahkan.
Untuk klasifikasi data yang akurat, jaringan saraf membutuhkan lapisan lebar. Selain itu, lapisan tradisional jaringan saraf tidak cocok untuk mewakili manipulasi penting dengan manifold; bahkan jika kita mengatur bobot secara manual, akan sulit untuk secara kompak mewakili transformasi yang kita inginkan.
Tautan ke sumber dan penjelasan[1] Banyak transformasi alami yang mungkin ingin Anda lakukan pada gambar, seperti menerjemahkan atau menskalakan objek di dalamnya, atau mengubah pencahayaan, akan membentuk kurva kontinu dalam ruang gambar jika Anda melakukannya secara terus menerus.
[2] Carlsson et al. menemukan bahwa tambalan lokal berupa botol klein.
[3] Hasil ini disebutkan dalam ayat Wikipedia tentang versi Isotop.