🐘 ☝️ 🖕 Rumus Tupper dan implementasi algoritma dalam Python 👨‍🎤 🌨️ 🚗

Alih-alih kata pengantar

Belum lama ini, di Internet, saya belajar tentang salinan perpustakaan Babylonia yang begitu indah dan menakjubkan sebagai formula Tapper . Sebaliknya, ini lebih merupakan ketimpangan Tupper daripada formula. Keunikan ketidaksetaraan ini adalah bahwa ia menciptakan citra sendiri di bagan. Lihat saja keajaiban ini!

gambar

(Sumber Wikipedia)

Apa yang Anda lihat dalam gambar adalah formula Jeff Tupper yang sama. Mungkin, setengah dari pembaca sudah pergi ke tungsten untuk menggambar hasil ketidaksetaraan ini ... Tapi ini tidak begitu sederhana. Seperti yang Anda lihat dalam gambar ini, rumus pada grafik dapat dilihat pada segmen sepanjang sumbu OY [k; k + 15]. Berapa angka misterius k ini? Di mana mendapatkannya? Masalahnya adalah bahwa ketidaksetaraan ini, menurut konsep perpustakaan Babel, dapat benar-benar menampilkan gambar apa pun dengan resolusi 106x17! Setiap gambar memiliki posisi sendiri pada grafik, sehingga memiliki angka unik k. Jadi, untuk setiap angka k ada satu gambar di seluruh grafik !

Untuk gambar yang diberikan, angka k adalah sebagai berikut:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

Sangat menarik untuk melihat orang-orang yang akan menggulir ke koordinat seperti itu untuk melihat formula

Terpikir oleh saya untuk menulis sebuah program dalam Python3 yang akan mengubah gambar menjadi angka k dan sebaliknya dan memberi tahu Anda tentang cara hebat lain untuk menyandikan gambar menjadi angka.

Teori

(Ditambahkan) Bagaimana cara kerjanya?

Mari kita lihat formula itu sendiri:
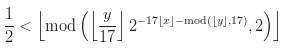
gambar

Mari kita definisikan sintaksnya:
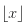
gambar

- angka dibulatkan ke bawah
mod (x, y) - sisa pembagian x oleh y

Dan kemudian, tampaknya, semuanya jelas.
Perhatikan bahwa x dan y dibulatkan. Pembulatan inilah yang akhirnya memberi kita gambar piksel
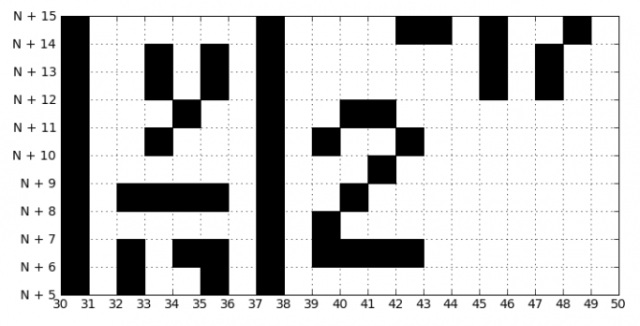
gambar

Sebutkan segala sesuatu yang dibulatkan di sisi kanan kesenjangan

a l p h a

$\ alpha$ .
Lalu

1 / 2 < [a l p h a] <=> 1 <= [a l p h a]

$1/2 <[\ alpha] <=> 1 <= [\ alpha]$

Yang jelas, karena seluruh ekspresi dibulatkan.

Misalkan y = 17r + q, di mana r adalah bagian integer dari pembagian y sebesar 17, dan r adalah sisa dari pembagian. Dengan demikian, kita bisa mengganti dalam formula

[y / 17]

$[y / 17]$ pada r, dan

m o d (y, 17)

$mod (y, 17)$ pada q.

Kami mendapatkan

1 <= m o d (q * 2^{- 17 - r}, 2)

$1 <= mod (q * 2 ^ {- 17-r}, 2)$

Atau yang lainnya

1 <= m o d (q / 2^{17 x + r}, 2)

$1 <= mod (q / 2 ^ {17x + r}, 2)$

mod (

a l p h a

$\ alpha$ , 2) mengambil 2 nilai - 0 atau 1. Oleh karena itu, ketidaksetaraan ini akan mengatakan apakah jumlahnya

q / 2^{17 x + r}

$q / 2 ^ {17x + r}$ bahkan atau tidak.

Perhatikan bahwa gambar dilihat dalam interval [N, N + 16], masing-masing

q = [y / 17]

$q = [y / 17]$ tetap konstan di seluruh ketinggian gambar, yang tidak dapat dikatakan tentang angka r (di seluruh gambar itu bervariasi dari 0 hingga 16).

Dan sekarang ceri di atas kue. Nomor

[q / 2^{17 x + r}]

$[q / {2 ^ {17x + r}}]$ akan aneh jika dan hanya jika nomor bit (17x + r) dalam representasi biner q sama dengan 1. Dan karena angka q terus berubah dengan tinggi dan representasi binernya, kita mendapatkan gambar unik setiap waktu! Persis seperti itulah rumus Tapper bekerja.

Sekarang mari kita lihat bagaimana cara menghitung ketinggian tempat kita ingin melihat gambar kita

Prinsip penghitungan angka k

Tupper sendiri menggambarkan perhitungan angka k untuk gambar 106x17 (ini penting!) Sebagai berikut:

Ubah gambar menjadi hitam dan putih
Baca setiap piksel dari bawah ke atas, dari kiri ke kanan dan letakkan di buffer. Jika pikselnya hitam - lalu masukkan 1, jika putih - 0.
Ubah biner menjadi desimal dan kalikan dengan 17
Untung!

Untuk mendapatkan gambar dari angka k, kami melakukan segala yang sebaliknya. Baiklah, mari kita coding!

Kodim

UPD: Dalam komentar, orang sedikit memperbaiki kode, membuatnya lebih sederhana dan lebih transparan. Artikel ini telah menerbitkan data pembaruan. Jika Anda ingin melihat versi kode yang lama - buka repositori github (sampai Anda mengkomitnya, tautkan di akhir artikel) dan di komentar

Dari k ke gambar

UPD

Atas permintaan komentator, ditambahkan cara baru untuk menghitung gambar menggunakan ketidaksetaraan ini dan k! Sekarang kita tidak akan melakukan manipulasi dengan nomor, transfer ke sistem biner, tetapi secara langsung mempengaruhi fungsi itu sendiri!

Menggunakan metode penyadap untuk memecahkan kode angka k

Kami mendapatkan nomor k dari pengguna, ~~dengan mata tertutup kami~~ membaginya dengan 17 dan menerjemahkannya ke dalam sistem biner.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:]

Kami memahami bahwa beberapa piksel awal bisa berwarna putih (sama dengan 0), masing-masing, untuk angka biner kami, bit pertama akan nol, dan ketika menerjemahkan angka ke dalam sistem desimal, nol awal ini akan hilang. Oleh karena itu, kami memeriksa ukuran angka biner yang dihasilkan, jika kurang dari 1802, lalu tambahkan nol ke awal.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary

Selanjutnya, nyatakan daftar dua dimensi di mana kami akan menyimpan informasi tentang setiap baris gambar. Lalu kita tuliskan semua bit yang kita baca (jangan lupa algoritma yang digunakan angka k - dari bawah ke atas, dari kiri ke kanan)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #

Mari kita coba tekan angka k, yang saya sebutkan di awal artikel, ke dalam program kami dan dapatkan yang berikut:

gambar

Seperti yang Anda lihat, semuanya bekerja untuk kami, dan sekarang kami dapat memecahkan kode k!

Menggunakan ketidaksetaraan untuk menghasilkan gambar dari k

Pertama, tulis fungsi dengan python:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2

Berkat operator // dan <<, implementasi fungsi telah sangat disederhanakan. Dijamin bahwa angka x dan y akan berupa bilangan bulat !

Kami kembali membuat daftar dua dimensi, di mana kami akan menyimpan bit gambar dan menulis informasi tentang setiap baris di dalamnya menggunakan loop

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2))

Dan kemudian, seperti pada contoh sebelumnya, kita menggambar menggunakan perpustakaan PIL.

Fungsi lengkapnya terlihat seperti ini:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists

Gambar dalam k

Baiklah, sekarang kita akan belajar untuk menyandikan gambar apa pun ke dalam angka k.

Pertama-tama kita mendapatkan gambar itu sendiri

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im

Periksa ukurannya

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !")

Kami membuat gambar menjadi hitam dan putih dan mulai membaca piksel demi piksel:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0'

Tetap hanya untuk mengkonversi ke sistem desimal dan kalikan dengan 17.

 k = int(byteset,2)*17 print(" :") print(k)

Baiklah, ayo kita tes!

Saya memutuskan untuk kode logo habr. Inilah gambar sumbernya:

gambar

Kami memulai program dan menentukan nama gambar:

gambar

Kami mendapat k berikut:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

Mari kita periksa di program kami sendiri.

Inilah gambar yang kami terima:

gambar

Itu sedikit terdistorsi karena terjemahan gambar sedikit bengkok dalam hitam dan putih.

Ringkasan

Kode sumber: Github

Sumber: artikel Wiki

Rumus Tupper dan implementasi algoritma dalam Python