Dalam sebuah artikel baru-baru ini, "
Modulasi Amplitudo dari Sinyal Sewenang-wenang, " penulisnya agak bingung mencoba menyajikan pemahamannya tentang pembentukan spektrum dengan modulasi amplitudo. Tetapi kurangnya ilustrasi dan kelebihan matematika yang melibatkan transformasi integral mencegah masyarakat untuk memahami pemikiran penulis dan menghargai artikel; sementara topiknya cukup sederhana - dan kami akan mencoba mempertimbangkannya lagi, kali ini dengan gambar dan Wolfram Mathematica.
Jadi, ide modulasi amplitudo adalah untuk mentransmisikan sinyal frekuensi rendah - suara atau musik - memodulasi sinyal frekuensi tinggi (pembawa), berkali-kali melebihi rentang yang dapat didengar dan menempati pita frekuensi sempit di udara. Modulasi itu sendiri dilakukan dengan hanya mengalikan sinyal dengan pembawa:

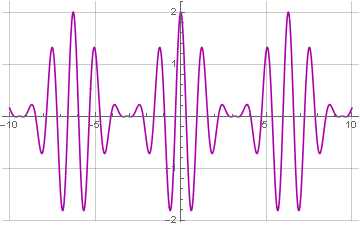
Di sini kita memiliki gelombang sinus dengan frekuensi 5:


Dan sinyalnya sendiri - dengan frekuensi 1:

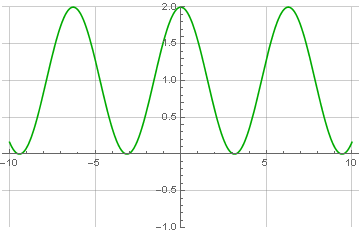
Anda mungkin memperhatikan bahwa sinyal digeser ke atas dan hanya memiliki nilai positif. Ini bukan kebetulan dan merupakan prasyarat untuk kemungkinan pemulihan yang benar berikutnya. Bagaimana cara mengembalikannya? Sangat mudah! Penting untuk menggeser fase sinyal termodulasi oleh 90 derajat (operasi yang dikenal sebagai
Hilbert transform ), dan menghitung akar jumlah kuadrat dari sinyal termodulasi dan terkonversi:

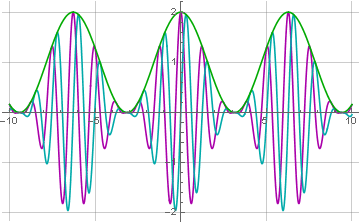
Dalam versi yang lebih sederhana (tetapi kasar), transformasi Hilbert dapat digantikan oleh penundaan sinyal oleh seperempat dari periode frekuensi pembawa, dan sinyal akhir dapat juga disaring oleh filter low-pass. Dalam versi yang lebih sederhana, Anda tidak dapat menghitung akar dan kuadrat sama sekali, tetapi saring sinyal dengan nilai absolut (yang biasanya digunakan pada penerima radio).
Sekarang mari kita lihat apa yang terjadi dengan spektra. Kami menghitung transformasi Fourier dari operator:


Karena fungsi Dirac delta bukan fungsi dalam pengertian klasik, grafiknya tidak dapat dibangun dengan cara standar; oleh karena itu, kami akan melakukannya secara manual menggunakan gaya yang diterima secara umum:

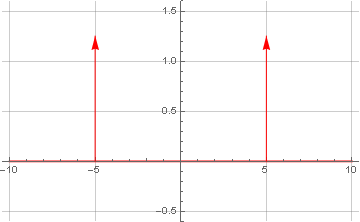
Diharapkan menerima frekuensi yang sama seperti pada rumus awal. Kehadiran satu lagi frekuensi yang sama, tetapi dengan tanda minus, tidak kebetulan - fenomena ini disebut
simetri Hermitian dan merupakan konsekuensi dari kenyataan bahwa fungsi yang dipermasalahkan adalah murni nyata dan dalam representasi kompleks memiliki komponen imajiner nol. Tidak adanya komponen imajiner dalam spektrum setelah transformasi disebabkan oleh kenyataan bahwa pada awalnya fungsi kita genap (simetris terhadap nol).
Sekarang kita membuat transformasi Fourier untuk sinyal itu sendiri:



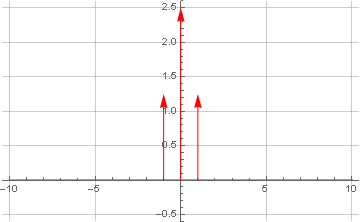
Di sini kita juga memperoleh fungsi delta Dirac di pusat koordinat - karena adanya komponen konstan dalam sinyal, yang tidak memiliki osilasi menurut definisi - yang memungkinkan kita untuk menganggapnya sebagai frekuensi nol.
Apa yang akan terjadi pada spektrum jika mereka dikalikan? Mari kita lihat:



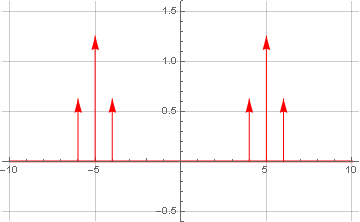
Dari teori, kita tahu bahwa perkalian dalam domain waktu setara dengan konvolusi dalam domain frekuensi (dan sebaliknya, yang banyak digunakan dalam penyaringan FIR). Dan karena salah satu sinyal yang mengalami konvolusi hanya terdiri dari satu frekuensi (positif dan negatif), maka sebagai akibat dari konvolusi, kami hanya mendapatkan transfer linear dari sinyal ke frekuensi (di kedua arah). Dan karena simetri tetap, sinyal masih tidak memiliki komponen imajiner.
Kami sekarang membawanya ke bentuk yang kompleks (
analitis ), dengan nolkan rentang frekuensi negatif:

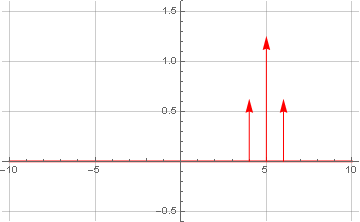
dan lakukan transformasi Fourier terbalik:


Karena fungsinya sekarang kompleks, untuk membuat grafiknya, perlu untuk mengekstrak komponen nyata dan imajiner secara terpisah:

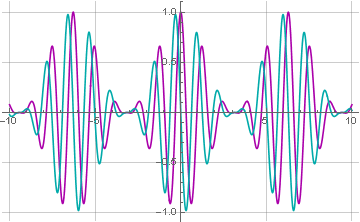
Sekarang sinyal kami memiliki komponen imajiner, yang merupakan sinyal asli bergeser 90 derajat. Ini akan lebih jelas jika kita merepresentasikan fungsi yang dihasilkan dalam bentuk trigonometri:

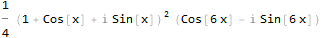
Belum terlalu jelas. Mari kita coba menyederhanakan:

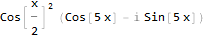
Sekarang lebih mirip kebenaran - dan seperti yang Anda lihat, fungsi sinyal asli kami juga telah disederhanakan. Mari kita coba mengembalikannya ke bentuk aslinya:
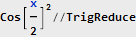

Faktor 1/2 tidak muncul secara kebetulan - setelah memusatkan setengah spektrum, kami mengurangi daya sinyal. Nah, sekarang, memiliki sinyal kompleks termodulasi, kita dapat mengambil modul ini untuk menghitung:

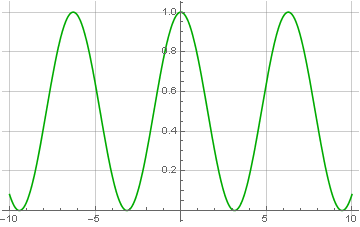
Modulus bilangan kompleks dihitung secara akurat melalui akar jumlah kuadrat dari komponen imajiner dan nyata. Dan dari sini jelas mengapa sinyal yang dikodekan hanya terdiri dari nilai-nilai positif - jika itu termasuk nilai-nilai negatif, maka setelah restorasi mereka juga akan menjadi positif, yang disebut overmodulation:

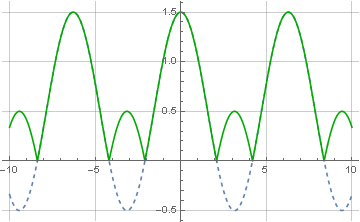
Pemulihan sinyal juga dimungkinkan dengan bantuan osilator lokal quadrature - ketika sinyal termodulasi kembali dikalikan dengan frekuensi pembawa, tetapi kali ini kompleks:





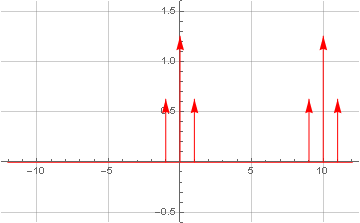
Karena kenyataan bahwa frekuensi kompleks dalam domain frekuensi hanya memiliki satu pulsa tanpa menduplikasi dalam rentang frekuensi negatif, sebagai akibat dari konvolusi kita mendapatkan transfer spektrum linier, di mana bagian negatif dari spektrum kembali ke pusat, dan yang positif bergerak lebih jauh, dan itu hanya akan disaring oleh filter low-pass.
Kesimpulan
Seperti yang Anda lihat, tidak ada yang rumit dalam mempertimbangkan modulasi amplitudo melalui transformasi Fourier; jika kita mempertimbangkannya secara eksklusif di tingkat sekolah, maka cukup untuk mengingat bahwa produk dari jumlah (pembawa) (mewakili sinyal dalam bentuk seri trigonometri) setara dengan jumlah produk (masing-masing anggota rangkaian secara individual pada frekuensi pembawa) - dan, oleh karena itu, setiap produk tersebut diuraikan menjadi jumlah dari dua sinusoid sesuai dengan formula yang sudah disuarakan oleh penulis artikel asli.
Pembaca yang penuh perhatian juga dapat memperhatikan bahwa karena modulasi menghasilkan spektrum simetris sehubungan dengan frekuensi pembawa, itu berarti ada redundansi data dan Anda hanya dapat meninggalkan satu sideband, sehingga mengurangi pita frekuensi yang ditempati di udara. Teknologi seperti itu memang
ada , tetapi itu adalah cerita yang sama sekali berbeda.