Salam untuk semua, dan terutama mereka yang tertarik pada matematika diskrit dan teori graf.
Latar belakang
Kebetulan, didorong oleh minat, saya mengembangkan layanan konstruksi wisata. rute. Tugasnya adalah merencanakan rute terbaik berdasarkan kota yang diminati pengguna, kategori perusahaan dan kerangka waktu. Nah, salah satu subtugas adalah untuk menghitung waktu tempuh dari satu institusi ke institusi lainnya. Karena saya masih muda dan bodoh, saya memecahkan masalah ini langsung, dengan algoritma Dijkstra, tetapi dalam keadilan perlu dicatat bahwa hanya dengan itu dimungkinkan untuk memulai iterasi dari satu node ke ribuan lainnya, caching jarak ini bukanlah suatu pilihan, institusi lebih dari 10k hanya di Moskow sendiri, dan keputusan-keputusan seperti jarak Manhattan di kota-kota kita sama sekali tidak berhasil.
Dan ternyata ternyata adalah mungkin untuk menyelesaikan masalah kinerja dalam masalah kombinatorik, tetapi sebagian besar waktu untuk memproses permintaan dihabiskan untuk mencari jalur yang tidak di-cache. Masalahnya diperumit oleh kenyataan bahwa grafik jalan Osm di Moskow cukup besar (setengah juta node dan 1,1 juta busur).
Saya tidak akan berbicara tentang semua upaya dan bahwa sebenarnya masalahnya dapat diselesaikan dengan memotong busur ekstra dari grafik, saya hanya akan memberitahu Anda bahwa pada titik tertentu saya sadar dan saya menyadari bahwa jika Anda mendekati algoritma Dijkstra dari sudut pandang pendekatan probabilistik, itu bisa linier.
Dijkstra untuk waktu logaritmik
Semua orang tahu, tetapi siapa yang tahu, membaca bahwa algoritma Dijkstra dengan menggunakan antrian dengan kompleksitas logaritmik menyisipkan dan menghapus dapat menyebabkan kompleksitas bentuk O (n log (n) + m log (n)). Saat menggunakan tumpukan Fibonacci, kompleksitas dapat dikurangi menjadi O (n * log (n) + m), tetapi masih tidak linier, tapi saya ingin.
Dalam kasus umum, algoritma antrian dijelaskan sebagai berikut:
Biarkan:
- V adalah himpunan simpul grafik
- E adalah himpunan tepi grafik
- w [i, j] adalah bobot tepi dari simpul i ke simpul j
- a - mulai vertex pencarian
- antrian verteks-q
- d [i] - jarak ke simpul ke-i
- d [a] = 0, untuk semua lainnya d [i] = + inf
Sementara q tidak kosong:
- v adalah simpul dengan minimum d [v] dari q
- Untuk semua simpul u yang ada transisi ke E dari simpul v
- jika d [u]> w [vu] + d [v]
- hapus u dari q dengan jarak d [u]
- d [u] = w [vu] + d [v]
- tambahkan u ke q dengan jarak d [u]
- hapus v dari q
Jika kita menggunakan pohon merah-hitam sebagai antrian, di mana penyisipan dan penghapusan terjadi di log (n), dan pencarian untuk elemen minimum serupa di log (n), maka kompleksitas algoritma adalah O (n log (n) + m log (n)) .
Dan di sini perlu diperhatikan satu fitur penting: secara teori tidak ada yang mempertimbangkan top beberapa kali. Jika titik telah diperiksa dan jarak ke titik tersebut telah diperbarui ke nilai yang salah, lebih besar dari nilai sebenarnya, asalkan cepat atau lambat sistem akan bertemu dan jarak ke u diperbarui ke nilai yang benar, maka diperbolehkan melakukan trik seperti itu. Tetapi perlu diperhatikan - satu simpul harus dipertimbangkan lebih dari 1 kali dengan probabilitas rendah.
Sortir Tabel hash
Untuk mengurangi waktu berjalan dari algoritma Dijkstra ke yang linier, struktur data diusulkan, yang merupakan tabel hash dengan nomor simpul (node_id) sebagai nilai. Saya perhatikan bahwa kebutuhan untuk array d tidak hilang, masih diperlukan untuk mendapatkan jarak ke simpul ke-i dalam waktu yang konstan.
Gambar di bawah ini menunjukkan contoh struktur yang diusulkan.
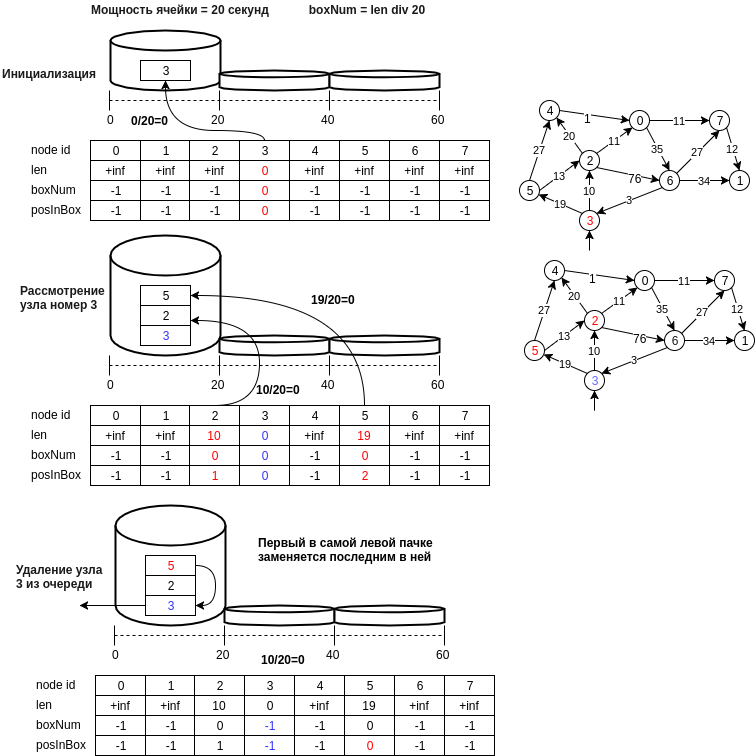
Mari kita jelaskan dalam langkah-langkah struktur data yang diusulkan:
- simpul u ditulis ke dalam sel dengan angka yang sama dengan d [u] // bucket_size, di mana bucket_size adalah kekuatan sel (misalnya, 20 meter, yaitu, sel pada angka 0 akan berisi node yang jaraknya akan berada pada kisaran [0, 20) meter )
- simpul terakhir dari sel non-kosong pertama, mis. operasi mengekstraksi elemen minimum akan dilakukan dalam O (1). Hal ini diperlukan untuk mempertahankan status pengidentifikasi nomor saat ini dari sel non-kosong pertama (min_el).
- operasi penyisipan dilakukan dengan menambahkan nomor simpul baru ke ujung sel dan juga menjalankan O (1), karena perhitungan jumlah sel terjadi dalam waktu yang konstan.
- operasi penghapusan, seperti dalam kasus tabel hash, enumerasi normal dimungkinkan, dan orang dapat membuat asumsi dan mengatakan bahwa dengan ukuran sel kecil ini juga O (1). Jika Anda tidak keberatan dengan memori (pada prinsipnya, dan tidak banyak yang dibutuhkan, array lain oleh n), maka Anda dapat membuat array posisi di dalam sel. Dalam hal ini, jika elemen dihapus di tengah sel, perlu untuk memindahkan nilai terakhir dalam sel ke lokasi yang dihapus.
- titik penting ketika memilih elemen minimum: minimal hanya dengan beberapa probabilitas, tetapi, algoritma akan melihat sel min_el sampai menjadi kosong dan cepat atau lambat elemen minimum nyata akan dipertimbangkan, dan jika kita secara tidak sengaja memperbarui nilai jarak ke node yang dapat dijangkau dari minimum, maka node yang berdekatan dengan minimum dapat kembali berada dalam antrian dan jarak ke mereka akan benar, dll.
- Anda juga dapat menghapus sel kosong hingga min_el, sehingga menghemat memori. Dalam hal ini, penghapusan node v dari antrian q perlu dilakukan hanya setelah mempertimbangkan semua node yang berdekatan.
- dan Anda juga dapat mengubah kekuatan sel, parameter untuk meningkatkan ukuran sel dan jumlah sel saat Anda perlu meningkatkan ukuran tabel hash.
Hasil Pengukuran
Cek dilakukan pada peta osm Moskow, dibongkar via osm2po di postgres, dan kemudian dimuat ke dalam memori. Tes ditulis dalam Java. Ada 3 versi grafik:
- grafik sumber - 0,43 juta node, 1,14 juta busur
- versi terkompresi dari grafik dengan 173k node dan 750k arc
- versi pejalan kaki dari versi grafik terkompresi, busur 450k, simpul 100k.
Di bawah ini adalah gambar dengan pengukuran pada berbagai versi grafik:

Pertimbangkan ketergantungan probabilitas untuk melihat kembali titik dan ukuran grafik:
| jumlah tampilan simpul | hitung simpul | probabilitas melihat kembali node |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0,9 |
| 431490 | 419594 | 2.8 |
Anda mungkin memperhatikan bahwa probabilitas tidak tergantung pada ukuran grafik dan agak spesifik untuk permintaan, tetapi kecil dan jangkauannya dikonfigurasi dengan mengubah daya sel. Saya akan sangat berterima kasih atas bantuan dalam membangun modifikasi probabilistik dari algoritma dengan parameter yang menjamin interval kepercayaan dalam kisaran di mana kemungkinan menonton berulang tidak akan melebihi persentase tertentu.
Pengukuran kualitatif juga dilakukan untuk secara praktis mengkonfirmasi perbandingan kebenaran hasil algoritma dengan struktur data baru, yang menunjukkan kebetulan lengkap panjang jalur terpendek dari 1000 node acak ke 1000 node acak lainnya pada grafik. (dan seterusnya 250 iterasi) ketika bekerja dengan tabel hash sorting dan pohon merah-hitam.
Kode sumber dari struktur data yang diusulkan terletak di tautan
PS: Saya tahu tentang algoritma Torup dan fakta bahwa itu memecahkan masalah yang sama dalam waktu linier, tapi saya tidak bisa menguasai pekerjaan mendasar ini dalam satu malam, walaupun saya mengerti ide itu secara umum. Setidaknya, seperti yang saya pahami, pendekatan lain diusulkan di sana, berdasarkan pada pembangunan pohon spanning minimal.
PSS Dalam seminggu saya akan mencoba mencari waktu dan membuat perbandingan dengan banyak Fibonacci dan sedikit kemudian menambahkan lobak github dengan contoh dan kode uji.