Ketika memecahkan masalah transmisi data melalui saluran yang diwakili oleh karakteristik frekuensi, Transformasi Fourier diterapkan - transfer sinyal dari domain waktu ke domain frekuensi dan sebaliknya. Lingkungan MATLAB memiliki fungsi lengkap untuk menyelesaikan masalah tersebut. Dalam karya ini, contoh menghitung dalam MATLAB reaksi sinyal yang ditransmisikan melalui garis yang karakteristiknya diukur pada frekuensi yang tidak sesuai dengan frekuensi transfer data dianalisis. Saya berharap contoh ini akan membuatnya lebih mudah untuk memahami fitur-fitur teknologi konversi sinyal di lingkungan MATLAB.
Kondisi tugas
Penting untuk menentukan perubahan bentuk sinyal digital biner yang melewati filter dan garis sinyal. Sinyal diatur oleh amplitudo dan laju transmisi. Filter urutan kedua, dinormalisasi ke frekuensi transfer data, diatur oleh konstanta waktu. Fungsi transfer dari garis sinyal diwakili oleh respons frekuensi yang diukur dalam bentuk kompleks.
Lingkungan yang digunakan untuk menghitung dan menampilkan data adalah MATLAB R2015a.
Relasi berikut yang diterbitkan di situs web
www.StatEye.org untuk versi metode GUI StatEye 3.0 [1, 2, 3] diambil sebagai contoh data awal.
Kecepatan data bps = 10.3125 Gbit / s. Konstanta waktu dari filter urutan kedua yang dinormalisasi adalah sama, kebalikannya adalah ¾ dari frekuensi transmisi data. Garis sinyal diwakili oleh respons frekuensi. Karakteristik diukur pada channel.f = 0,006495: 0,0012475: 20 GHz. Jumlah titik pengambilan sampel yang ditentukan dari transformasi Fourier: poin = 2 ^ 13.
Gambar 1 menunjukkan transfer data, urutan, dan hasil pengolahan data yang dibahas dalam makalah ini. Transisi dari domain waktu ke domain frekuensi dan sebaliknya dilakukan dengan menggunakan algoritma Fast Fourier Transform (FFT).
Gambar 1. Saluran data. Sinyal input iSignal.Tx, sinyal keluaran dari filter iSignal.Filter_out, garis sinyal keluaran iSignal.Rx. Karakteristik yang ditunjukkan dalam diagram dibahas di bawah ini.Urutan perhitungan
Dalam karya ini, perhitungan utama dilakukan dalam domain frekuensi. Untuk ini, sinyal asli dari domain waktu dipindahkan ke domain frekuensi menggunakan transformasi Fourier, dengan mengalikan karakteristik spektral sinyal, filter dan garis sinyal, sinyal output dari jalur ditemukan, yang ditransfer dari domain frekuensi ke domain waktu oleh transformasi Fourier terbalik.
Kecepatan transfer data dua kali lebih tinggi dari frekuensi pengiriman data. Frekuensi maksimum dari max jalur sinyal yang diukur (channel.f) = 20 GHz. Pada frekuensi ini, data dapat ditransmisikan pada kecepatan 40 Gbit / s (sebagai 2 * maks (channel.f)).
Kecepatan transfer data maksimum, yang tidak melebihi kecepatan transmisi maksimum pada garis sinyal 40 Gbit / s dan laju transmisi ganda bps = 10.3125 Gbit / s, adalah fmax = 30,9375 Gbit / s, multiplisitas N = 3 (N = fmax / bps). Selanjutnya, fmax digunakan sebagai frekuensi pembatas untuk menghitung respons sinyal menggunakan transformasi Fourier.
Terjemahan dari sinyal input ke dalam domain frekuensi
Diskrititas waktu untuk membangun sinyal input (bit data) dalam domain waktu Ts = 1 / fmax; Ts = 3.232e-11 s. Dinormalisasi berkenaan dengan durasi sinyal, timeline waktu terdiri dari 2 ^ 13 poin (poin), skala mencakup array titik waktu berikut = bps / Ts. * (1: poin). Sinyal tunggal diskrit pada laju transmisi bps = 10.3125 Gbit / s dan kuantisasi dengan periode Ts = 1 / fmax terdiri dari tiga titik dalam kisaran 10 hingga 11 unit waktu normal. Sinyal amplitudo unit dapat dibangun di tempat lain di timeline, tetapi lebih baik untuk mundur dari tepi untuk sepenuhnya melihat latar belakang dan proses transisi dari sinyal output. Sinyal pulsa (bit data) yang dibangun menggunakan perintah MATLAB berikut ditunjukkan pada Gambar 2.
iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;
Gambar 2. Input sinyal pulsa iSignal.Tx, bit data.Terjemahan dari sinyal iSignal.Tx ke dalam domain frekuensi dilakukan oleh fungsi FFT berikut.
iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);
Fungsi transformasi Fourier fft membangun spektrum simetris sinyal di wilayah frekuensi positif dan negatif, frekuensi maksimumnya berada di tengah spektrum (lihat Gambar 3). Fungsi fftshift mengembalikan spektrum dengan menggeser ke tengah frekuensi nol dari sinyal seperti yang ditunjukkan pada Gambar 4.
Resolusi frekuensi spektrum adalah fs = fmax / points; Frekuensi spektrum berkisar dari -fmax / 2 hingga fmax / 2-fs dan sama dengan f = -fmax / 2: fs: fmax / 2-fs;
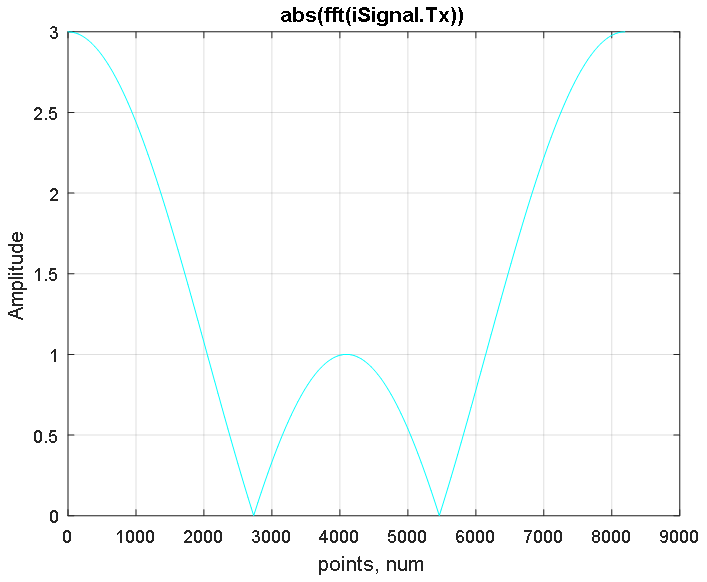Gambar 3. Respon amplitudo dari spektrum bergeser dari sinyal iSignal.Tx yang diperoleh dengan menggunakan FFT.
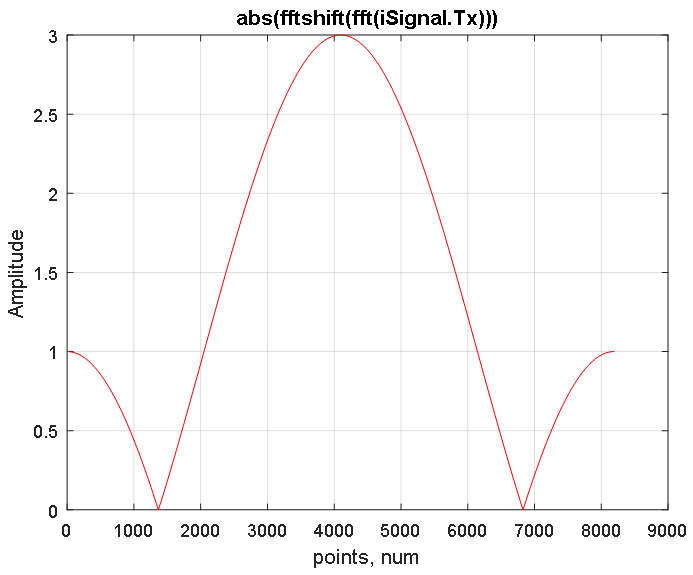Gambar 4. Respon amplitudo dari spektrum sinyal iSignal.Tx yang ditunjukkan pada Gambar 3. 2 ^ 13 sampel disajikan. Jumlah rata-rata di 4097 sesuai dengan frekuensi nol. Frekuensi negatif terletak di sisi kiri (dari 1 hingga 4096 poin), dan wilayah frekuensi positif di sisi kanan (dari 4098 hingga 8192 poin).Fungsi transfer filter low pass dinormalisasi
Dalam contoh ini, fungsi transfer filter orde kedua memiliki formulir
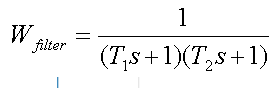
di mana T1 dan T2 adalah konstanta waktu filter. Frekuensi 1 / T1 adalah sama dan 1 / T2 diatur relatif terhadap frekuensi di mana data ditransmisikan: 1 / T1 = 1 / T2 = 0,75 * bps (bps = 10,3125 Gbit / s).
Bandwidth filter yang dinormalisasi
f_nrm =fmax/bps/points.*(-points/2:points/2-1).
Operator
s = f_nrm .* j;
Karakteristik fase amplitudo dari filter yang dinormalisasi untuk frekuensi positif dan negatif yang dinormalisasi sehubungan dengan frekuensi transmisi sinyal ditunjukkan pada Gambar 5. Karakteristik frekuensi-amplitudo logaritmik dari filter ditunjukkan pada Gambar 6.
Gambar 5. Karakteristik fase amplitudo dari filter dinormalisasi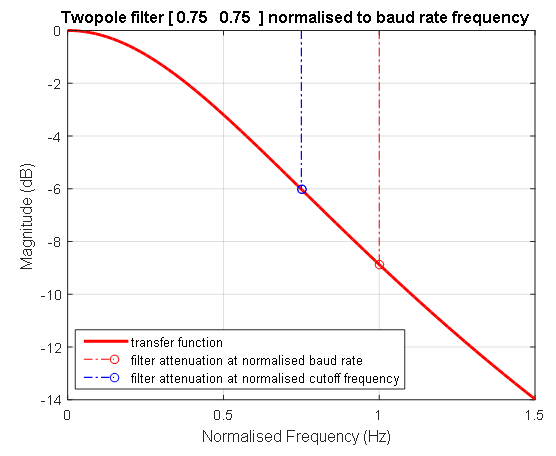
Gambar 6. Respons frekuensi fase amplitudo logaritmik dari filter yang dinormalisasi. Garis putus-putus biru menunjukkan posisi frekuensi filter dengan nilai 0,75 dari frekuensi di mana data sedang dikirim. Pada frekuensi ini (1 / T1 = 1 / T2), koefisien transmisi filter orde kedua adalah -6 desibel. Garis putus-putus merah menunjukkan frekuensi unit di mana data sedang dikirim.Terjemahan hasil pengukuran garis sinyal ke jenis fungsi transfer
Karakteristik fase-amplitudo yang diukur dari jalur sinyal mencakup 1.599 sampel dalam pita hingga 20 GHz dengan langkah tetap 12.475 MHz. Ini berisi nilai-nilai frekuensi berikut: channel.f = 0,006495: 0,0012475: 20 GHz. Awalnya, garis sinyal diwakili oleh karakteristik empat terminal. Karakteristik ini telah diubah dan digunakan dalam contoh sebagai fungsi kompleks satu dimensi.
Frekuensi karakteristik jalur sinyal yang diperoleh sebagai hasil pengukuran tidak sesuai dengan frekuensi spektrum sinyal input yang merupakan kelipatan dari frekuensi transmisi data. Selain itu, spektrum garis sinyal hanya mengandung frekuensi positif dan tidak mengandung frekuensi di wilayah nol. Spektrum sinyal input berisi frekuensi positif, nol dan negatif.
Untuk mengubah karakteristik saluran sinyal menjadi fungsi transfer - karakteristik yang frekuensinya bersamaan dengan frekuensi spektrum sinyal input, langkah-langkah berikut diambil.
1. Perhitungan amplitudo karakteristik garis pada frekuensi nol dengan mengekstrapolasinya. Untuk ini, dari sepuluh titik karakteristik amplitudo yang paling dekat dengan frekuensi nol, koefisien polinomial linier ditemukan yang mendekati karakteristik amplitudo:
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);
Koefisien polinomial kedua yang ditemukan sama dengan amplitudo karakteristik pada frekuensi nol:
channel.dc = a(2);
2. Respon fase pada frekuensi nol diambil sama dengan nol.
channel.dcPhase = 0.00;
3. Perhitungan ulang saluran amplitudo. Karakteristik saluran dan fase. Saluran fase dengan nilai pada frekuensi nol dilakukan pada frekuensi spektrum sinyal input (f = -fmax / 2: fmax / poin: fmax / 2-fmax / poin) dengan ekstrapolasi karakteristik untuk area frekuensi nol dan negatif:
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);
Fungsi transfer yang diperoleh - respons frekuensi fase amplitudo dari saluran di wilayah frekuensi rendah ditunjukkan pada Gambar 7. Karakteristik frekuensi-amplitudo dari garis sinyal yang diukur dan fungsi transfer yang dihitung dalam rentang frekuensi penuh ditunjukkan pada Gambar 8. Karakteristik yang sama dalam ruang fase ditunjukkan pada Gambar 9.
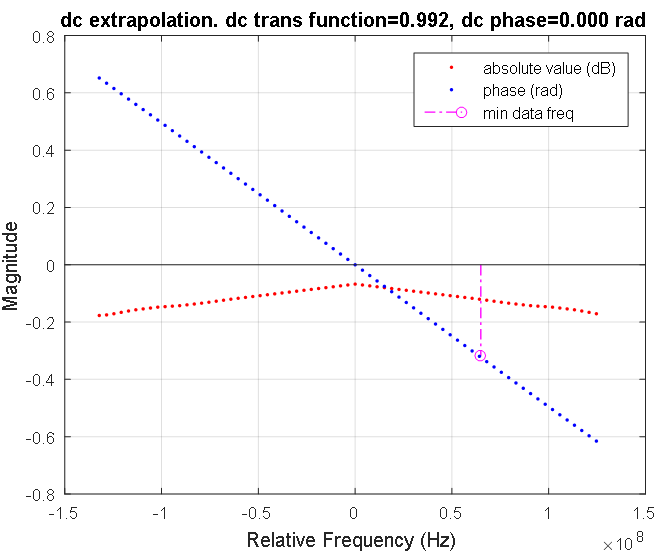Gambar 7. Fungsi transfer saluran sinyal di wilayah frekuensi rendah. Titik merah dan biru masing-masing menunjukkan karakteristik amplitudo dan fase diskrit. Respons amplitudo ditunjukkan dalam desibel, fase dalam radian. Garis merah muda menandai frekuensi terendah dari karakteristik garis sinyal yang diukur. Koefisien transmisi pada frekuensi nol adalah 0,992.
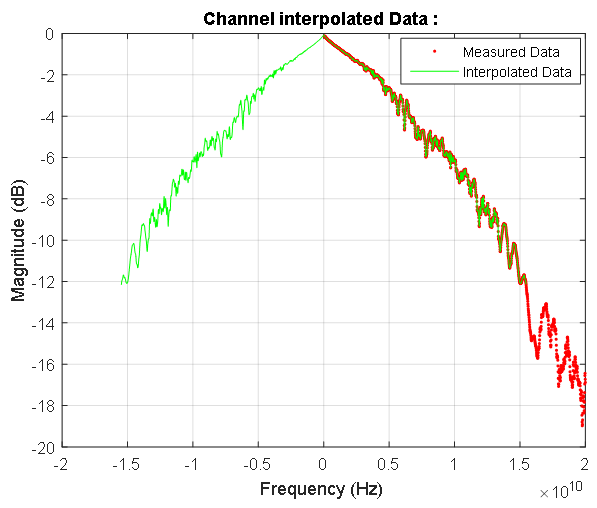Gambar 8. Respon frekuensi dari garis sinyal. Titik biru menunjukkan data kompleks dari garis yang diukur. Ketergantungan simetris yang dihitung dari penguatan jalur sinyal pada frekuensi spektrum sinyal input disorot dalam warna merah. Di wilayah frekuensi nol, karakteristik ini ditunjukkan pada Gambar 7.
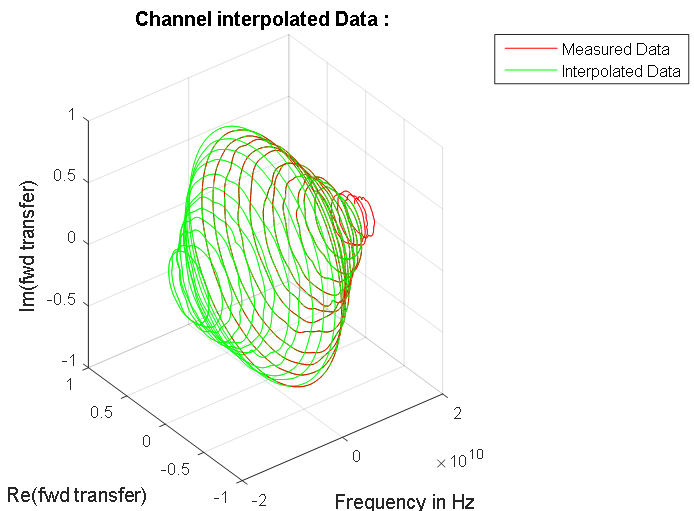Gambar 9. Karakteristik frekuensi fase amplitudo dari garis data yang diukur dan spektrum yang dinormalisasi.Perhitungan Respon Sinyal
Respons (respons terhadap efek input) dalam domain frekuensi diperoleh dengan mengalikan spektrum sinyal dengan produk dari fungsi transfer elemen yang menghubungkan reaksi dengan sinyal input. Dalam kasus kami, sinyal melewati filter dan jalur sinyal.
Invert Fourier transform ifft digunakan untuk mentransfer sinyal dari domain frekuensi ke domain waktu.
Output filter dalam domain waktu iSignal.Filter_out dihitung sebagai
TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));
Sinyal output dari garis iSignal.Rx sama dengan produk dari spektrum sinyal input dan fungsi transfer filter dan garis sinyal dengan transfer selanjutnya dari sinyal yang diterima dari domain frekuensi ke domain waktu.
TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));
Respons filter terhadap input pulsa ideal dan respons saluran ditunjukkan pada Gambar 10.
Gambar 10. Filter output (grafik merah) dan output jalur data (grafik hijau). Sinyal input filter - pulsa tunggal ditunjukkan pada Gambar 2. Input jalur sinyal adalah sinyal output filter.Aplikasi. Digunakan m-code MATLAB
Daftar bibliografi
1. IEEE802.3ap. 10.3125Gbps Hasil Simulasi NRZ Menggunakan "StatEye" dan "Signal to Interference Model" pada Komponen Saluran Cascaded. Shannon Sawyer dan Charles Moore / Agilent Technologies. 24 Januari 2005
www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf2. Apa itu StatEye. Satuan Tugas IEEE 803.3ap. 16 September 2004
www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf3. Stat Eye / Perjanjian IBM. Steve Anderson. Xilinx, Inc.
www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf