Pelatihan Keberlanjutan GAN

Gagasan GAN pertama kali diterbitkan oleh Jan Goodfellow Generative Adversarial Nets, Goodfellow et al 2014 , setelah itu GAN adalah salah satu model generatif terbaik.

Seperti halnya model generatif lainnya, tugas GAN adalah membangun model data, dan lebih khusus lagi, mempelajari cara menghasilkan sampel dari distribusi sedekat mungkin dengan distribusi data (biasanya ada kumpulan data dengan ukuran terbatas, distribusi data yang ingin kami modelkan).

GAN memiliki sejumlah besar keuntungan, tetapi mereka memiliki satu kelemahan signifikan - mereka sangat sulit untuk dilatih.

Baru-baru ini, sejumlah karya tentang keberlanjutan GAN telah dirilis:

• Optimalisasi keturunan GAN gradien stabil secara lokal, Vaishnavh Nagarajan, J. Zico Kolter, 2017
• The Numerics of GANs, Lars Mescheder et al, 2017

Terinspirasi oleh ide-ide mereka, saya melakukan sedikit riset.

Saya mencoba membuat teks sesederhana mungkin dan, jika mungkin, hanya menggunakan matematika yang paling sederhana. Sayangnya, untuk membenarkan mengapa kita dapat mempertimbangkan sifat-sifat bidang vektor 2 dimensi, kita harus menggali sedikit ke arah kalkulus variasi. Tetapi jika seseorang tidak terbiasa dengan istilah-istilah ini, Anda dapat dengan aman melanjutkan segera ke pertimbangan bidang vektor 2 dimensi untuk berbagai jenis GAN.

Kami sekarang akan mencoba melihat di bawah tenda prosedur pelatihan dan memahami apa yang terjadi di sana.

GAN, masalah utama

GAN terdiri dari dua jaringan saraf: diskriminator dan generator. Generator - memungkinkan Anda untuk mengambil sampel dari beberapa distribusi (biasanya disebut distribusi generator). Diskriminator menerima sampel input dari dataset asli dan generator dan belajar untuk memprediksi dari mana sampel ini berasal (dataset atau generator).

Skema GAN:



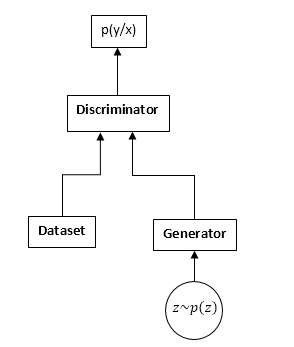
Proses pelatihan GAN adalah sebagai berikut:

1. Kami mengambil n sampel dari dataset dan sampel m dari generator.
2. Kami memperbaiki bobot generator dan memperbarui parameter diskriminator. Ini adalah tugas klasifikasi yang umum. Kami hanya tidak perlu melatih diskriminator sampai konvergensi. Dan bahkan lebih sering juga mengganggu.
3. Kami memperbaiki bobot diskriminator dan memperbarui bobot generator, sehingga diskriminator mulai berpikir bahwa sampel kami berasal dari dataset dan bukan dari generator.
4. Kita ulangi 1-3, sampai pembeda dan generator mencapai keseimbangan (yaitu, tidak ada yang lain bisa "menipu" yang lain).

Kami tidak akan memeriksa secara detail proses pembelajaran GAN. Di Internet, dan pada hubr khususnya, ada banyak artikel yang menjelaskan proses ini secara rinci.

Kami akan tertarik pada sesuatu yang sangat berbeda. Yaitu, karena fakta bahwa kami bersaing dengan dua jaringan saraf, tugas tidak lagi menjadi pencarian minimum (maksimum), tetapi dalam kasus-kasus tertentu berubah menjadi pencarian untuk titik pelana (mis., Pada langkah 2 dan 3 kami mencoba fungsional yang sama memaksimalkan dengan parameter diskriminator dan meminimalkan dengan parameter generator), dan pada langkah yang lebih umum 2 dan 3 kita dapat mengoptimalkan fungsional yang sama sekali berbeda. Jelas, masalah minimax adalah kasus khusus optimasi berbagai fungsional - satu fungsional diambil dengan tanda yang berbeda.

Mari kita lihat ini dalam formula. Kami berasumsi bahwa pd (x) adalah distribusi dari mana dataset disampel, pg (x) adalah distribusi generator, D (x) adalah output dari diskriminator.

Saat melatih seorang diskriminator, kami sering memaksimalkan fungsi tersebut:

$$

$$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$

Vektor Gradien:

$$

$$v = \ \ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ theta D (x) \ dx \ + \ \ int {\ frac {p_g (x) )} {1 \ - \ D (x)} \ nabla_ \ theta D (x) dx}}$$

Saat melatih generator, kami memaksimalkan:

$$

$$I \ = \ - \ int {p_g (x) log (1 \ - \ D (x)) dx}$$

Vektor gradien dalam hal ini:

$$

$$u \ = \ \ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) log (1 \ - \ D (x)) dx}$$

Di masa depan, kita akan melihat bahwa fungsional dapat diganti masing-masing dengan:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Dimana $$$f_1, f_2, f_3$ dipilih sesuai aturan tertentu. Ngomong-ngomong, Ian Goodfellow menggunakan dalam artikel aslinya $$$f_1 dan f_2$ seperti ketika melatih diskriminator reguler, dan $$$f_3$ memilih untuk meningkatkan gradien pada tahap awal pelatihan:

$$

$$f_1 \ kiri (x \ kanan) = log \ kiri (x \ kanan), \ f_2 \ kiri (x \ kanan) = log \ kiri (1 \ - \ x \ kanan), f_3 \ kiri (x \ kanan) = log \ kiri (x \ kanan)$$

Sekilas, tugas itu tampaknya sangat mirip dengan tugas belajar yang biasa dengan gradient descent (pendakian). Lalu, mengapa semua orang yang datang ke pelatihan GAN setuju bahwa itu sangat sulit?

Jawabannya terletak pada struktur bidang vektor, yang kami gunakan untuk memperbarui parameter jaringan saraf. Dalam kasus masalah klasifikasi biasa, kami hanya menggunakan vektor gradien, yaitu bidang yang potensial (fungsional yang dioptimalkan sendiri adalah potensi bidang vektor ini). Dan bidang vektor potensial memiliki beberapa sifat yang luar biasa, salah satunya adalah tidak adanya kurva tertutup. Artinya, tidak mungkin berjalan berputar-putar di bidang ini. Tetapi ketika melatih GAN, terlepas dari kenyataan bahwa bidang vektor untuk generator dan diskriminator berpotensi secara terpisah (sama gradien), bidang vektor total tidak akan berpotensi. Dan ini berarti bahwa di bidang ini bisa ada kurva tertutup, yaitu kita bisa berjalan dalam lingkaran. Dan ini sangat, sangat buruk.

Timbul pertanyaan: mengapa, sama saja, kita berhasil melatih GAN dengan cukup sukses, mungkin bidangnya masih irrotasional (potensial)? Dan jika demikian, mengapa hal ini sangat rumit?
Saya akan terus maju, sayangnya, bidang ini tidak potensial, tetapi memiliki sejumlah properti yang baik. Sayangnya, bidang ini juga sangat sensitif terhadap parameterisasi jaringan saraf (pilihan fungsi aktivasi, penggunaan DropOut, BatchNormalisasi, dll.). Tetapi hal pertama yang pertama.

GAN "Gradien"

Kami akan mempertimbangkan fungsi pembelajaran GAN dalam bentuk paling umum:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Kita perlu mengoptimalkan kedua fungsi secara bersamaan. Dengan asumsi bahwa D (x) dan pg (x) adalah fungsi yang benar-benar fleksibel, mis. kita dapat mengambil nomor apa pun di titik mana pun, terlepas dari titik lainnya. Itu adalah fakta yang terkenal dari kalkulus variasi - Anda perlu mengubah fungsi ke arah turunan variasional fungsional ini (secara umum, analog lengkap kenaikan gradien).

Kami menulis turunan variasional:

$$

$$\ frac {\ partial J} {\ partial D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ partial I} {\ partial p_g (x)} = f_3 (D (x))$$

Kami hanya akan mempertimbangkan fungsional pertama (untuk pembeda), untuk yang kedua semuanya akan sama.

Tetapi mengingat bahwa sebenarnya kita dapat mengubah fungsi hanya di set fungsi yang diwakili oleh jaringan saraf kita, kita akan menulis:

$$$$ menampilkan $$ ∆D (x) = \ frac {\ partial D (x)} {\ partial θ_j} Δθ_j $$ menampilkan $$

perubahan parameter jaringan, secara umum, gradient descent (kenaikan) yang biasa:

$$$$ menampilkan $$ ∆θj = \ frac {\ partial J} {\ partial θ_j} μ $$ menampilkan $$

μ adalah tingkat pembelajaran. Nah, turunan sehubungan dengan parameter jaringan:

$$

$$\ frac {\ partial J} {\ partial \ theta_j} = \ int {\ frac {\ partial J} {\ partial D (y)} \ frac {\ partial D (y)} {\ partial \ theta_j} dy }$$

Dan sekarang kita sedang menyusun semuanya:

$$

$$∆D (x) = \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ int {\ frac {\ partial J} {\ partial D (y)} \ frac { \ partial D (y)} {\ partial \ theta_j} dy} \ mu \ = \ mu \ int \ frac {\ partial J} {\ partial D (y)}} \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ frac {\ partial D (x)} {\ partial \ theta_j} dy \ = \} \ mu \ int {\ frac {\ partial J} {\ partial D (y )} K_ \ theta (x, y) dy}$$

Dimana: $$$K_ \ theta (x, y) \ = \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ frac {\ partial D (x)} {\ partial \ theta_j} \ }$

Saya belum pernah melihat fitur ini dalam literatur tentang pembelajaran mesin, jadi saya akan menyebutnya inti parametrik sistem.

Nah, atau jika kita pergi ke langkah-langkah berkesinambungan dalam waktu (dari persamaan perbedaan ke persamaan), kita mendapatkan:

$$

$$\ frac {d} {dt} D (x) \ = \ \ int {\ frac {\ partial J} {\ partial D (y)} K_ \ theta (x, y) dy}$$

Persamaan ini menunjukkan hubungan internal dari bidang asli (pointwise untuk diskriminator) dan parameterisasi jaringan saraf. Kami memperoleh persamaan yang sangat mirip untuk generator.

Mengingat bahwa K (x, y) (kernel parametrik) adalah fungsi pasti positif (well, bagaimana ia dapat direpresentasikan sebagai produk skalar dari gradien pada titik-titik yang sesuai), kita dapat menyimpulkan bahwa setiap perubahan dalam fungsi yang dilatih (diskriminator dan generator) milik ruang Hilbert dihasilkan oleh inti, yaitu K (x, y). Saya ingin tahu apakah mungkin untuk mendapatkan hasil yang bermakna di sini. Tetapi kita belum akan melihat ke arah itu, tetapi kita akan melihat ke arah yang lain.

Seperti yang Anda lihat, stabilitas GAN ditentukan oleh dua komponen: turunan variasional dari fungsional dan parameterisasi dari jaringan saraf. Tugas kami adalah untuk melihat bagaimana bidang ini berperilaku pointwise, yaitu, jika jaringan kami benar-benar dapat mewakili fungsi apa pun. Tugas berubah menjadi analisis bidang vektor dua dimensi. Dan ini, saya pikir, adalah kekuatan kita.

Keberlanjutan

Jadi, kami mempertimbangkan bidang vektor berikut:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ partial J} {\ partial D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ partial I} {\ partial p_g (x)}$$

Jelas, persamaan ini dapat dipertimbangkan hanya untuk satu titik x, dengan mempertimbangkan bagaimana turunan variasional kami terlihat seperti:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

Persyaratan pertama untuk sistem persamaan ini adalah sisi kanan harus menuju ke 0 ketika:
$$$p_d = p_g$

Kalau tidak, kami akan mencoba untuk melatih model, yang jelas tidak akan menyatu dengan solusi yang benar. Yaitu D harus menjadi solusi untuk persamaan berikut:

$$

$$f_1 ^ \ prime (D) \ + \ f_2 ^ \ prime (D) \ = \ 0$$

Kami menyatakan solusi ini sebagai $$$D0$ .

Mengingat fakta bahwa pg (x) adalah kepadatan probabilitas di sisi kanan, kita dapat menambahkan angka apa pun tanpa melanggar turunannya. Untuk memberikan 0 sisi kanan pada titik yang diinginkan, kurangi nilainya dalam t. $$$D0$ (ini harus dilakukan jika kita ingin mempertimbangkan pg pointwise - transisi dari bidang parameter oleh kepadatan probabilitas ke bidang bebas).

Akibatnya, kami memperoleh bidang berikut:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

Mulai sekarang, kita akan mempelajari poin diam dan stabilitas bidang semacam ini.
Kita dapat mempelajari dua jenis stabilitas: lokal (di sekitar titik diam) dan global (menggunakan metode fungsi Lyapunov).

Untuk mempelajari stabilitas lokal, perlu untuk menghitung matriks Jacobi lapangan.
Agar lapangan menjadi "stabil" secara lokal, perlu bahwa nilai eigen memiliki bagian nyata yang negatif.

Berbagai jenis GAN

1. GAN klasik

   
   
   Dalam GAN klasik, kami menggunakan logloss biasa:
   

   $$

   $$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$
   
   Untuk pelatihan diskriminator, perlu memaksimalkannya, untuk generator, untuk menguranginya. Dalam kasus ini, bidangnya akan terlihat seperti ini:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + \ log (\ frac {1} {2})$$
   
   Mari kita lihat bagaimana parameter (pg dan D) akan berkembang di bidang ini. Untuk melakukan ini, gunakan skrip Python sederhana ini:
   
   
   Skrip

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Untuk titik awal $$$p_g = 0,9, D = 0,25$ akan terlihat seperti ini:
   
   
   
   Titik sisa bidang tersebut adalah: pg = pd dan D = 0,5
   
   Orang dapat dengan mudah memverifikasi bahwa bagian-bagian nyata dari nilai-nilai eigen dari matriks Jacobi negatif, yaitu bidang tersebut stabil secara lokal.
   Kami tidak akan berurusan dengan bukti keberlanjutan global. Tetapi jika ini sangat menarik, Anda dapat bermain-main dengan skrip Python dan memastikan bahwa bidang tersebut stabil untuk nilai awal yang valid.

2. Modifikasi oleh Jan Goodfellow

   
   Kita sudah membahas di atas bahwa Ian Goodfellow dalam artikel aslinya menggunakan versi GAN yang sedikit dimodifikasi. Untuk versinya, fungsinya adalah sebagai berikut:
   

   $$

   $$f_1 \ kiri (x \ kanan) = log \ kiri (x \ kanan), \ f_2 \ kiri (x \ kanan) = log \ kiri (1 \ - \ x \ kanan), f_3 \ kiri (x \ kanan) = log \ kiri (x \ kanan)$$
   
   Bidang akan terlihat seperti ini:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   Skrip python akan sama, hanya fungsi bidangnya yang berbeda:
   
   
   Skrip

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Dan dengan data awal yang sama, gambarnya terlihat seperti ini:
   
   
   
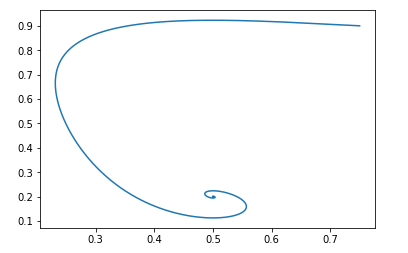
   Dan lagi, mudah untuk memverifikasi bahwa lapangan akan stabil secara lokal.
   Yaitu, dari sudut pandang konvergensi, modifikasi semacam itu tidak merusak sifat-sifat GAN, tetapi memiliki keunggulan dalam hal pelatihan jaringan saraf.

3. Wasserstein gan

   
   Mari kita lihat pandangan populer GAN lainnya. Fungsi yang dioptimalkan terlihat seperti ini:
   

   $$

   $$J \ = \ \ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   Di mana D termasuk kelas fungsi 1-Lipschitz sehubungan dengan x.
   Kami ingin memaksimalkannya dengan D dan menguranginya dengan pg.
   
   Jelas, dalam hal ini: $$$f_1 \ kiri (x \ kanan) = x, \ f_2 \ kiri (x \ kanan) = - x, \ f_3 \ kiri (x \ kanan) = x$
   
   Dan bidangnya akan terlihat seperti ini:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   Di bidang ini, lingkaran dengan pusat pada suatu titik mudah ditebak. $$$p_g = p_d, D = 0$ .
   Artinya, jika kita menyusuri bidang ini, kita akan selalu berputar-putar.
   
   Berikut adalah contoh lintasan di bidang tersebut:
   
   
   
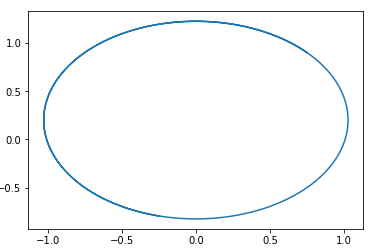
   Pertanyaannya adalah, mengapa kemudian melatih GAN semacam ini? Jawabannya sangat sederhana - analisis ini tidak memperhitungkan fakta properti 1-Lipschitz dari D. Artinya, kita tidak dapat mengambil fungsi sewenang-wenang. Ngomong-ngomong, ini sesuai dengan hasil penulis ... dari artikel tersebut. Untuk menghindari berjalan dalam lingkaran, mereka merekomendasikan pelatihan diskriminator untuk bertemu: Wasserstein GAN

4. Opsi GAN Baru

   
   Pemilihan Fitur $$$f_1, f_2 dan f_3$ Anda dapat membuat berbagai opsi GAN. Persyaratan utama untuk fungsi-fungsi ini adalah untuk memastikan adanya titik istirahat yang "benar" dan stabilitas titik ini (lebih disukai global, tetapi setidaknya lokal). Saya memberi pembaca kesempatan untuk memperoleh pembatasan pada fungsi f1, f2 dan f3, yang diperlukan untuk stabilitas lokal. Mudah - pertimbangkan saja persamaan kuadrat untuk nilai eigen dari matriks Jacobi.
   
   Saya akan memberikan contoh GAN tersebut:
   

   $$

   $$f_1 (x) \ = \ -0.5x ^ 2, \ f_2 (x) \ = \ x, \ f_3 (x) \ = \ -x$$
   
   Sekali lagi, saya menyarankan agar pembaca sendiri membangun bidang GAN ini dan membuktikan stabilitasnya. (Omong-omong, ini adalah salah satu dari sedikit bidang yang bukti kestabilan globalnya elementer - cukup pilih fungsi Lyapunov, jarak ke titik istirahat). Hanya memperhitungkan bahwa titik sisanya adalah D = 1.

Kesimpulan dan penelitian lebih lanjut

Dapat dilihat dari analisis di atas bahwa semua GAN klasik (dengan pengecualian Wassertein GAN, yang memiliki metode sendiri untuk meningkatkan stabilitas) memiliki bidang "baik". Yaitu mengikuti bidang-bidang ini memiliki titik istirahat tunggal di mana distribusi generator sama dengan distribusi data.

Jadi, mengapa, melatih GAN adalah tugas yang sulit. Jawabannya sederhana - parameterisasi jaringan saraf. Dengan parameterisasi "buruk", kita juga bisa jalan-jalan di lingkaran. Misalnya, percobaan saya menunjukkan bahwa, misalnya, menggunakan BatchNormalisasi di salah satu jaringan segera mengubah bidang menjadi yang tertutup. Dan aktivasi Relu bekerja paling baik.

Sayangnya, saat ini tidak ada satu pun cara untuk secara teoritis memeriksa elemen mana dari jaringan saraf bagaimana mengubah bidang. Ini akan membuktikan kepada saya prospektif untuk menyelidiki sifat-sifat kernel parametrik dari sistem - $$$K_ \ theta (x, y)$ .

Saya juga ingin berbicara tentang cara untuk mengatur bidang GAN dan melihat ini dari perspektif bidang dua dimensi. Pertimbangkan algoritma Penguatan Pembelajaran dari perspektif ini. Dan masih banyak lagi. Tapi sayangnya, artikelnya ternyata terlalu besar, jadi lebih banyak tentang itu lain waktu.