Selama bertahun-tahun saya telah menonton snooker sebagai olahraga. Ia memiliki segalanya: keindahan memukau dari permainan intelektual, keanggunan pukulan kiem dan ketegangan psikologis persaingan. Tapi ada satu hal yang saya tidak suka - sistem peringkatnya .
Kekurangan utamanya adalah ia hanya memperhitungkan fakta pencapaian turnamen tanpa memperhitungkan “kompleksitas” pertandingan. Model Elo kehilangan kelemahan ini, yang memantau "kekuatan" para pemain dan memperbaruinya tergantung pada hasil pertandingan dan "kekuatan" lawan. Namun, itu tidak cocok dengan sempurna: diyakini bahwa semua pertandingan diadakan dalam kondisi yang sama, dan di snooker mereka dimainkan hingga sejumlah frame menang (partai). Untuk menjelaskan fakta ini, saya mempertimbangkan model lain, yang saya sebut EloBeta .
Artikel ini mempelajari kualitas model Elo dan EloBet berdasarkan hasil pertandingan snooker. Penting untuk dicatat bahwa tujuan utama adalah untuk menilai "kekuatan" para pemain dan membuat peringkat "adil", daripada membangun model prediksi untuk mendapatkan keuntungan.

Peringkat snooker saat ini didasarkan pada prestasi pemain di turnamen dengan "berat" yang berbeda. Sekali waktu, hanya Kejuaraan Dunia yang diperhitungkan. Setelah penampilan banyak kompetisi lain, daftar poin dikembangkan bahwa pemain bisa mendapatkan ketika ia mencapai tahap tertentu dari turnamen. Sekarang peringkat memiliki bentuk jumlah uang hadiah "bergerak" yang telah diperoleh pemain selama (kurang-lebih) dua tahun kalender terakhir.
Sistem ini memiliki dua keunggulan utama: sederhana (memenangkan banyak uang - naik peringkat) dan dapat diprediksi (jika Anda ingin naik ke tempat tertentu - menangkan sejumlah uang, semua hal lain dianggap sama). Masalahnya adalah bahwa dengan metode ini kekuatan (keterampilan, bentuk) dari lawan tidak diperhitungkan . Argumen bantahan yang biasa adalah: "Jika seorang pemain telah mencapai tahap akhir turnamen, maka dia menurut definisi adalah pemain kuat saat ini" ("pemain yang lemah tidak memenangkan turnamen"). Kedengarannya cukup meyakinkan. Namun, dalam snooker, seperti dalam olahraga apa pun, peran kasing harus diperhitungkan: jika seorang pemain "lebih lemah", ini tidak berarti bahwa ia tidak akan pernah bisa menang "lebih kuat" dalam pertandingan melawan pemain. Itu terjadi lebih jarang daripada skenario sebaliknya. Di sinilah model Elo hadir.
Ide dari model Elo adalah bahwa setiap pemain dikaitkan dengan peringkat numerik. Sebuah asumsi diperkenalkan bahwa hasil permainan antara dua pemain dapat diprediksi berdasarkan perbedaan dalam peringkat mereka: nilai yang lebih tinggi berarti probabilitas yang lebih tinggi untuk memenangkan pemain "kuat" (dengan peringkat lebih tinggi). Peringkat Elo didasarkan pada "kekuatan" saat ini , dihitung berdasarkan hasil pertandingan dengan pemain lain. Ini menghindari kelemahan utama dalam sistem peringkat resmi saat ini. Pendekatan ini juga memungkinkan Anda memperbarui peringkat pemain selama turnamen untuk merespons secara numerik performa baiknya.
Memiliki pengalaman praktis dengan peringkat Elo, menurut saya dia harus menunjukkan dirinya dengan baik di snooker. Namun, ada satu kendala: itu dirancang untuk kompetisi dengan satu jenis pertandingan . Tentu saja, ada variasi untuk memperhitungkan keuntungan dari lapangan tuan rumah dalam sepak bola dan gerakan pertama dalam catur (keduanya dalam bentuk menambahkan jumlah poin penilaian tetap ke pemain dengan keunggulan). Di snooker, pertandingan dimainkan dalam format "best of N": pemain yang memenangkan kemenangan pertama n= fracN+12 bingkai (pesta). Kami juga akan memanggil format ini "hingga n kemenangan. "
Secara intuitif, memenangkan pertandingan hingga 10 kemenangan (final dari turnamen serius) harus lebih sulit untuk pemain "lemah" daripada memenangkan pertandingan 4 kemenangan (putaran pertama turnamen Home Nations saat ini). Ini diperhitungkan dalam model EloBet saya.
Gagasan menggunakan peringkat Elo di snooker sama sekali tidak baru. Misalnya, ada karya-karya berikut:
- Snooker Analyst menggunakan sistem penilaian "Elo like" (lebih seperti model Bradley - Terry ). Idenya adalah untuk memperbarui peringkat berdasarkan perbedaan antara jumlah frame "nyata" dan "diharapkan" yang dimenangkan. Pendekatan ini menimbulkan pertanyaan. Tentu saja, perbedaan yang lebih besar dalam jumlah frame kemungkinan besar menunjukkan perbedaan kekuatan yang lebih besar, tetapi pada awalnya pemain tidak memiliki tugas seperti itu. Di snooker, tujuannya adalah "hanya" untuk memenangkan pertandingan, mis. Menangkan sejumlah frame sebelum lawan.
- Diskusi ini ada di forum dengan penerapan model Elo dasar.
- Ini dan ini adalah kegunaan nyata dalam snooker amatir.
- Mungkin ada karya lain yang saya lewatkan. Saya akan sangat berterima kasih atas informasi tentang topik ini.
Ulasan
Artikel ini ditujukan untuk pengguna bahasa R yang tertarik mempelajari peringkat Elo, dan untuk penggemar snooker. Semua eksperimen ditulis dengan gagasan dapat direproduksi. Kode disembunyikan di bawah spoiler, memiliki komentar dan menggunakan paket rapi , sehingga dapat menarik bagi pengguna untuk membaca sendiri R. Diasumsikan bahwa semua kode yang disajikan dijalankan secara berurutan. Satu file dapat ditemukan di sini .
Artikel ini disusun sebagai berikut:
- Bagian Model menjelaskan pendekatan Elo dan EloBet dengan implementasi dalam R.
- Bagian Eksperimen menjelaskan rincian dan motivasi perhitungan: data dan metodologi apa yang digunakan (dan mengapa), serta hasil apa yang diperoleh.
- Bagian EloBet Ranking Study berisi hasil penerapan model EloBet ke data snooker nyata. Dia akan lebih tertarik pada pecinta snooker.
Kami akan membutuhkan inisialisasi berikut.
Kode inisialisasi# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
Model
Kedua model didasarkan pada asumsi berikut:
- Ada seperangkat pemain tetap yang harus diperingkat dari "terkuat" (tempat pertama) ke "terlemah" (tempat terakhir).
- Peringkat berdasarkan asosiasi pemain i dengan peringkat numerik ri : Angka yang mewakili "kekuatan" pemain (nilai yang lebih tinggi berarti pemain yang lebih kuat).
- Semakin besar perbedaan peringkat sebelum pertandingan, semakin kecil kemungkinan kemenangan pemain "lemah" (dengan peringkat lebih rendah).
- Peringkat diperbarui setelah setiap pertandingan berdasarkan hasil dan peringkat sebelum itu.
- Kemenangan atas lawan yang "lebih kuat" harus disertai dengan peningkatan peringkat yang lebih besar daripada kemenangan atas lawan yang "lebih lemah". Dengan kekalahan, yang terjadi adalah sebaliknya.
Elo
Kode Model Elo #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
Elo Model memperbarui peringkat dengan prosedur berikut:
Perhitungan probabilitas pemain tertentu yang memenangkan pertandingan (sebelum dimulai). Probabilitas satu pemain menang (kami akan memanggilnya "pertama") dengan pengenal i dan diberi peringkat ri lebih dari pemain lain ("kedua") dengan pengenal j dan diberi peringkat rj sama dengan
Pr(ri,rj)= frac11+10(rj−ri)/400
Dengan pendekatan ini, perhitungan probabilitas mematuhi asumsi ketiga.
Menormalkan perbedaan menjadi 400 adalah cara matematika untuk mengatakan perbedaan mana yang dianggap "besar." Angka ini dapat diganti dengan parameter model. xi Namun, ini hanya mempengaruhi penyebaran peringkat di masa depan dan biasanya berlebihan. Nilai 400 cukup standar.
Dengan pendekatan umum, probabilitas kemenangan sama L(rj−ri) dimana L(x) beberapa fungsi yang benar-benar meningkat dengan nilai dari 0 hingga 1. Kami akan menggunakan kurva logistik. Studi yang lebih lengkap dapat ditemukan di artikel ini .
Perhitungan hasil pertandingan S . Dalam model dasar, itu sama dengan 1 dalam hal kemenangan pemain pertama (kekalahan yang kedua), 0,5 pada saat hasil seri dan 0 jika kekalahan dari pemain pertama (kemenangan yang kedua).
Pembaruan peringkat :
- delta=K cdot(S−Pr(ri,rj)) . Ini adalah jumlah perubahan peringkat. Dia menggunakan koefisien K (satu-satunya parameter model). Lebih sedikit K (dengan probabilitas yang sama) berarti perubahan peringkat yang lebih kecil - modelnya lebih konservatif, mis. dibutuhkan lebih banyak kemenangan untuk "membuktikan" perubahan kekuatan. Di sisi lain, lebih banyak K berarti lebih banyak kredibilitas dengan hasil terbaru daripada peringkat saat ini. Pilihan "optimal" K adalah cara untuk membuat sistem peringkat "baik" .
- r(baru)i=ri+ delta , r(new)j=rj− delta .
Komentar :
- Seperti dapat dilihat dari formula pembaruan, jumlah peringkat semua pemain yang dipertimbangkan tidak berubah seiring waktu: peringkat meningkat karena penurunan peringkat lawan
- Pemain tanpa pertandingan dimainkan dikaitkan dengan peringkat awal 0. Biasanya, nilai 1500 atau 1000 digunakan, tetapi saya tidak melihat alasan lain selain psikologis. Memperhatikan komentar sebelumnya, menggunakan nol berarti jumlah semua peringkat selalu nol, yang cantik dengan caranya sendiri.
- Penting untuk memainkan sejumlah pertandingan tertentu agar peringkatnya mencerminkan "kekuatan" pemain. Ini menimbulkan masalah: pemain yang baru ditambahkan mulai dengan peringkat 0, yang mungkin bukan yang terkecil di antara pemain saat ini. Dengan kata lain, "pendatang baru" dianggap "lebih kuat" daripada beberapa pemain lain. Anda dapat mencoba untuk melawan ini dengan prosedur pembaruan peringkat eksternal saat memasukkan pemain baru.
Mengapa algoritma seperti itu masuk akal? Dalam hal pemerataan peringkat delta selalu sama 0,5 cdotK . Misalkan, misalnya, itu ri=0 dan rj=400 . Ini berarti kemungkinan menang pemain pertama adalah frac11+10 sekitar0,0909 , yaitu dia akan memenangkan 1 pertandingan dari 11 pertandingan.
- Jika menang, dia akan menerima kenaikan kira-kira 0,909 cdotK , yang lebih dari dalam hal pemerataan peringkat.
- Dalam hal kekalahan, dia akan menerima pengurangan sekitar 0,0909 cdotK , Yang kurang dari dalam hal pemerataan peringkat.
Ini menunjukkan bahwa model Elo mematuhi asumsi kelima: kemenangan atas lawan adalah "lebih kuat" disertai dengan peningkatan peringkat yang lebih besar daripada kemenangan atas lawan yang "lebih lemah", dan sebaliknya.
Tentu saja, model Elo memiliki fitur praktisnya sendiri (tingkat tinggi). Namun, yang paling penting untuk penelitian kami adalah sebagai berikut: diasumsikan bahwa semua pertandingan diadakan dengan pijakan yang sama. Ini berarti bahwa jarak pertandingan tidak diperhitungkan: kemenangan dalam pertandingan hingga 4 kemenangan dihargai dengan cara yang sama dengan kemenangan dalam pertandingan hingga 10 kemenangan. Di sinilah model panggung EloBeta.
EloBeta
Kode Model EloBet #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
Dalam model Elo, perbedaan peringkat secara langsung memengaruhi probabilitas memenangkan seluruh pertandingan. Gagasan utama dari model EloBet adalah pengaruh langsung dari perbedaan peringkat pada probabilitas menang dalam satu frame dan perhitungan eksplisit probabilitas pemain yang menang. n bingkai sebelum lawan .
Pertanyaannya tetap: bagaimana cara menghitung probabilitas seperti itu? Ternyata ini adalah salah satu masalah tertua dalam sejarah teori probabilitas dan memiliki namanya sendiri - masalah pembagian taruhan (Masalah poin). Presentasi yang sangat bagus dapat ditemukan di artikel ini . Menggunakan notasinya, probabilitas yang diinginkan adalah:
P(n,n)= jumlah limit2n−1j=n2n−1 pilihjpj(1−p)2n−1−j
Di sini P(n,n) - probabilitas pemain pertama yang memenangkan pertandingan sebelumnya n kemenangan; p - probabilitas kemenangannya dalam satu frame (lawan memiliki probabilitas 1−p ) Dengan pendekatan ini, diasumsikan bahwa hasil frame dalam pertandingan independen satu sama lain . Ini mungkin diragukan, tetapi merupakan asumsi yang diperlukan untuk model ini.
Apakah ada cara yang lebih cepat untuk menghitung? Ternyata jawabannya adalah ya. Setelah beberapa jam konversi rumus, percobaan praktis, dan pencarian di internet, saya menemukan properti berikut pada fungsi beta tidak lengkap yang teregulasi Ix(a,b) . Mengganti m=k, n=2k−1 ke properti ini dan mengganti k pada n ternyata P(n,n)=Ip(n,n) .
Ini juga kabar baik bagi pengguna R, karena Ip(n,n) dapat dihitung sebagai pbeta(p, n, n) . Catatan : kasus umum probabilitas kemenangan di n bingkai sebelum lawan menang m dapat juga dihitung sebagai Ip(n,m) dan pbeta(p, n, m) masing-masing. Ini membuka peluang bagus untuk memperbarui kemungkinan menang selama pertandingan .
Prosedur pembaruan peringkat dalam kerangka model EloBet memiliki formulir berikut (dengan peringkat yang diketahui ri dan rj jumlah bingkai yang dibutuhkan untuk menang n dan hasil pertandingan S , seperti dalam model Elo):
- Perhitungan probabilitas kemenangan pemain pertama dalam satu frame : p=Pr(ri,rj)= frac11+10(rj−ri)/400 .
- Perhitungan probabilitas kemenangan pemain ini dalam pertandingan : PrBeta(ri,rj)=Ip(n,n) . Misalnya, jika p sama dengan 0,4, maka probabilitas memenangkan pertandingan sebelum 4 kemenangan turun menjadi 0,29, dan dalam "hingga 18 kemenangan" - menjadi 0,11.
- Pembaruan peringkat :
- delta=K cdot(S−PrBeta(ri,rj)) .
- r(baru)i=ri+ delta , r(new)j=rj− delta .
Catatan : karena perbedaan peringkat secara langsung mempengaruhi probabilitas untuk menang dalam satu frame, dan tidak di seluruh pertandingan, nilai koefisien optimal yang lebih rendah harus diharapkan K : bagian dari nilai delta berasal dari efek penguat PrBeta(ri,rj) .
Gagasan untuk menghitung hasil pertandingan berdasarkan probabilitas menang dalam satu frame bukanlah hal yang sangat baru. Di situs kepengarangan François Labelle ini, Anda dapat menemukan perhitungan daring tentang kemungkinan memenangkan yang terbaik N "Cocok, bersama dengan fungsi-fungsi lainnya. Aku senang melihat bahwa hasil perhitungan kami bertepatan. Namun, aku tidak bisa menemukan sumber untuk memperkenalkan pendekatan seperti itu pada prosedur pembaruan untuk peringkat Elo. Seperti sebelumnya, aku akan sangat berterima kasih atas informasi tentang topik ini.
Saya hanya bisa menemukan artikel ini dan deskripsi sistem Elo di server game backgammon (FIBS). Ada juga analog berbahasa Rusia . Di sini, durasi pertandingan yang berbeda diperhitungkan dengan mengalikan perbedaan peringkat dengan akar kuadrat dari jarak pertandingan. Namun, tampaknya tidak memiliki justifikasi teoretis.
Eksperimen
Eksperimen memiliki beberapa tujuan. Berdasarkan hasil pertandingan snooker:
- Tentukan nilai koefisien terbaik K untuk kedua model.
- Untuk mempelajari stabilitas model dalam hal akurasi probabilitas prediktif.
- Untuk mempelajari efek dari menggunakan turnamen "undangan" pada peringkat.
- Buat riwayat peringkat yang adil untuk musim 2017/18 untuk semua pemain profesional.
Data
Kode Pembuatan Data Eksperimen # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
Kami akan menggunakan data snooker dari paket comperank . Sumber aslinya adalah snooker.org . Hasil diambil dari pertandingan berikut:
- Pertandingan dimainkan di musim 2016/17 atau 2017/18 .
- Pertandingan ini merupakan bagian dari turnamen snooker “profesional” , yaitu:
- Itu adalah dari jenis "Undangan", "Kualifikasi", atau "Peringkat". Kami juga akan membedakan dua set pertandingan: "semua pertandingan" (dari semua data turnamen) dan "pertandingan resmi" (tidak termasuk turnamen undangan). Ada dua alasan untuk ini:
- Dalam turnamen undangan, tidak semua pemain memiliki kesempatan untuk mengubah peringkat mereka. Ini tidak selalu buruk dalam kerangka model Elo dan EloBet, tetapi ia memiliki "semburat ketidakadilan".
- Ada keyakinan bahwa para pemain "menganggap serius" hanya untuk pertandingan penilaian resmi. Catatan : sebagian besar turnamen Undangan adalah bagian dari Championship League, yang saya pikir diterima oleh sebagian besar pemain.
tidak terlalu serius dalam bentuk latihan dengan kemampuan menghasilkan uang. Kehadiran turnamen ini dapat mempengaruhi peringkat. Selain "Liga Kejuaraan" ada turnamen undangan lainnya: "Kejuaraan Cina 2016", keduanya "Juara Liga Champions", keduanya "Master", "Master Hong Kong", "Game Dunia 2017", "Master Rumania 2017".
- Menjelaskan snooker tradisional (bukan 6 merah atau Power Snooker) antara pemain individu (bukan tim).
- Kedua jenis kelamin dapat terlibat (bukan hanya pria atau wanita).
- Pemain dari segala usia dapat mengambil bagian (tidak hanya senior atau "di bawah 21").
- Ini bukan "Shoot-Out" karena turnamen ini jika tidak disimpan dalam database snooker.org.
- Pertandingan benar-benar terjadi : hasilnya adalah hasil pertandingan nyata yang melibatkan kedua pemain.
- Pertandingan diadakan antara dua profesional . Daftar profesional diambil untuk musim 2017/18 (131 pemain). Keputusan ini tampaknya menjadi yang paling kontroversial, seperti penghapusan pertandingan dengan partisipasi amatir "menutup mata" menjadi kekalahan profesional dari amatir. Ini mengarah pada keuntungan yang tidak adil dari para pemain ini. Tampak bagi saya bahwa keputusan seperti itu diperlukan untuk mengurangi peringkat inflasi yang akan terjadi ketika memperhitungkan kecocokan dengan amatir. Pendekatan lain adalah mempelajari para profesional dan amatir bersama-sama, tetapi ini tampaknya tidak masuk akal dalam kerangka penelitian ini. Kekalahan seorang amatir profesional dianggap sebagai kehilangan kesempatan untuk meningkatkan peringkat.
Jumlah pertandingan terakhir yang digunakan adalah 4118 untuk "semua pertandingan" dan 3644 untuk "pertandingan resmi" (masing-masing 62,9 dan 55,6 per pemain).
Metodologi
Kode Fungsi Eksperimen #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 . , . :
- K :
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 dimana T — , |T| — , St — , Pt — ( ). , " " .
- K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
Hasil
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
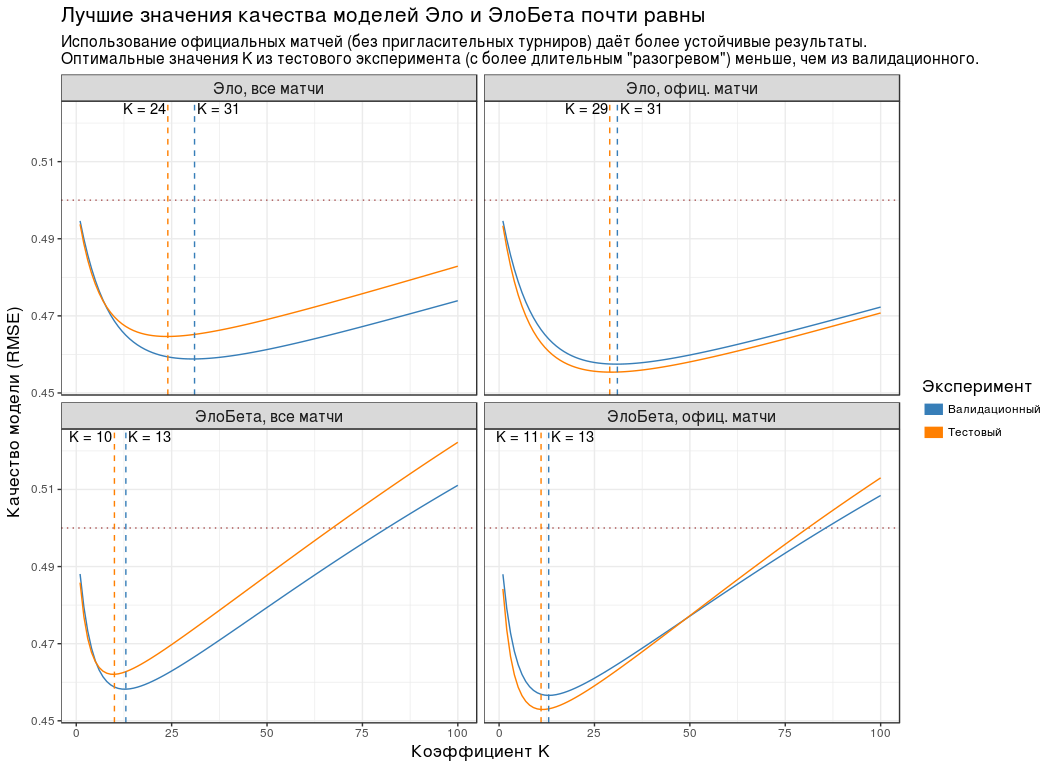
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | Tanggal 29 | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
Karena , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , n , .
" " ( K=10 ) - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92.2 | 5 | 660 250 | 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82.8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 |
:
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
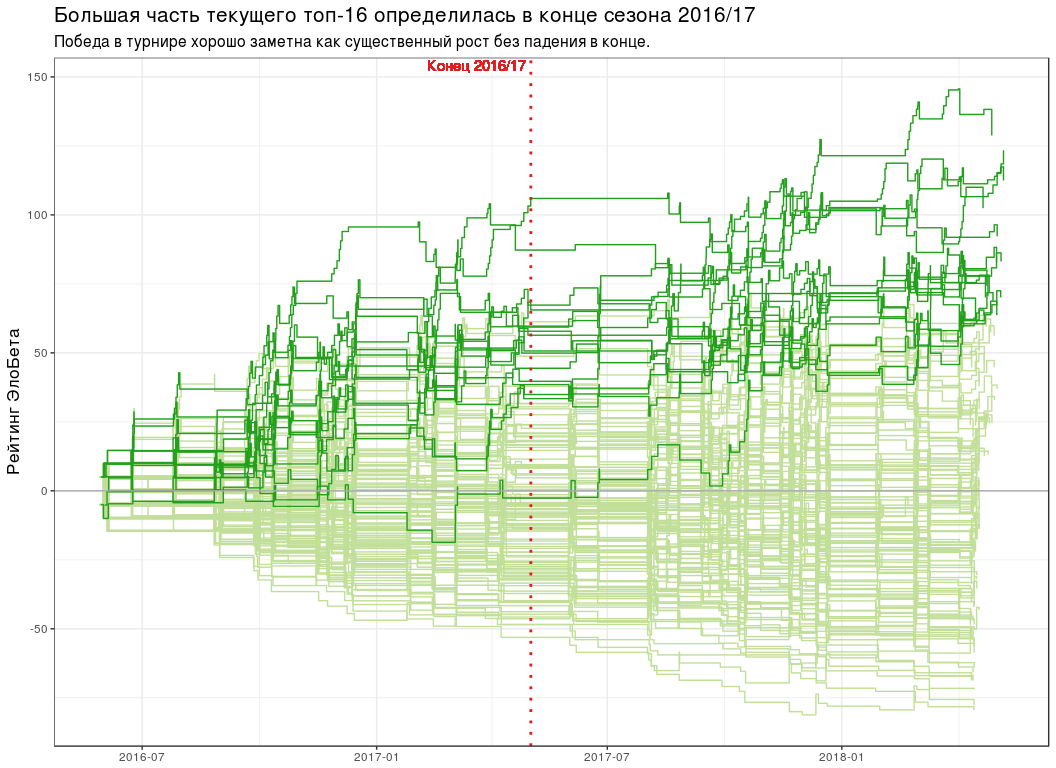
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
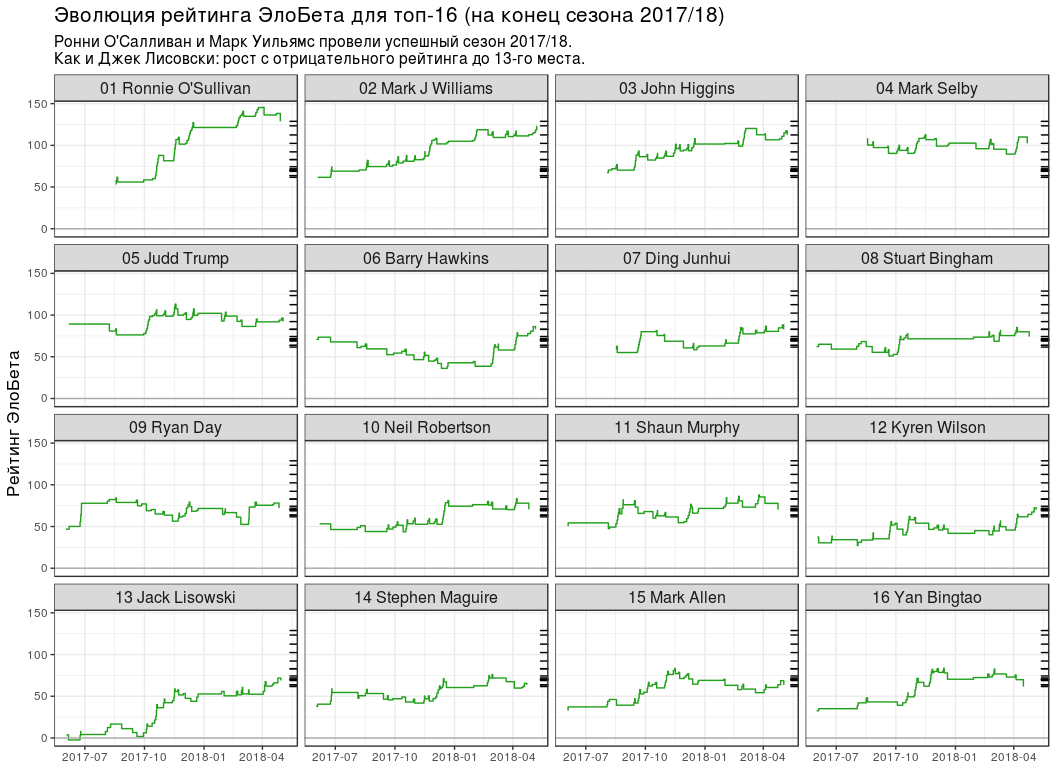
Kesimpulan
- " " R :
pbeta(p, n, m) . - — "best of N " ( n ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1