Pembenaran matematis Pythagoras dari skala musik

Sebuah bab dari buku Alexander Voloshinov "Matematika dan Seni" (Moscow: Enlightenment, 1992)

Yang Mulia Pythagoras menolak penilaian musik berdasarkan bukti perasaan. Dia berargumen bahwa kebajikannya harus dirasakan oleh pikiran, dan karena itu menilai musik bukan dengan telinga, tetapi atas dasar harmoni matematis dan menemukannya cukup untuk membatasi studi musik menjadi satu oktaf.

Plutarch

Sebenarnya, kita berbicara tentang sistem Pythagoras. Apa itu gamma dan skala dalam musik?

Gamma , atau skala , adalah urutan bunyi (langkah) dari beberapa sistem musik (fret), yang terletak, mulai dari bunyi utama (nada utama), dalam urutan naik atau turun. Nama "gamma" berasal dari huruf Yunani Gγ (gamma), yang pada Abad Pertengahan melambangkan nada yang lebih rendah dari skala, dan kemudian seluruh skala.

Karakteristik paling penting dari suara musik adalah nada , yang merupakan refleksi dalam kesadaran frekuensi osilasi dari tubuh yang terdengar, seperti string. Semakin tinggi frekuensi osilasi senar, semakin tinggi pula bunyinya bagi kita.

Setiap suara individu tidak membentuk sistem musik dan, jika tidak terlalu keras, tidak menyebabkan banyak reaksi. Namun, kombinasi dua bunyi dalam kasus lain ternyata menyenangkan dan harmonis, dan dalam kasus lain, sebaliknya, "memotong" telinga. Kombinasi dua suara yang disepakati disebut konsonan , kombinasi tidak konsisten disebut disonansi . Jelas bahwa konsonan atau disonansi dua nada ditentukan oleh jarak ketinggian antara nada-nada ini atau intervalnya.

Interval antara dua nada adalah nomor seri pitch nada atas relatif terhadap yang lebih rendah dalam skala ini, dan koefisien interval I _{21 dari} dua nada adalah rasio frekuensi nada atas dengan frekuensi nada lebih rendah ^* :

(6.1)

^* ( Dalam teori musik, konsep interval dan koefisien interval tidak dibedakan secara ketat. Mengikuti tradisi, kita sering merujuk pada koefisien interval untuk singkatnya sebagai interval. )

Mari kita sekarang mempertimbangkan seperangkat suara tertentu dengan menekan, misalnya, beberapa tombol pada piano. Kemungkinan besar, kita akan mendapatkan seperangkat suara yang tidak jelas, seperti kata mereka, baik gudang maupun fret. Dalam kasus lain, suara tampaknya cocok, rukun satu sama lain, tetapi kombinasi mereka akan tampak kasar, belum selesai. Saya ingin melanjutkan urutan ini ke nada tertentu, yang dalam sistem suara ini tampaknya paling stabil, dasar dan disebut tonik . Jadi, suara dalam sistem musik saling berhubungan oleh dependensi tertentu, beberapa di antaranya tidak stabil dan condong ke yang lain - stabil .

Tetapi tidak hanya tonik dan kombinasi suara yang stabil dan tidak stabil menentukan sifat sistem musik. Sangat mudah untuk memastikan dengan menekan delapan tombol putih berturut-turut dari nada ke (skala ke alam utama ) dan dari nada a ( minor alami ), skala ini terdengar berbeda: yang pertama - utama - terdengar ceria dan ringan, dan yang kedua - kecil - sedih dan mendung ^* . Oleh karena itu, ada karakteristik lain dari sistem suara - mood: mayor atau minor. Jadi, kita sampai pada salah satu konsep paling kompleks dalam teori musik - konsep fret.

^* ( Sifat bunyi fret, tentu saja, tidak didefinisikan secara kasar dan tegas. Pertanyaan ini sangat halus, dan kita akan membicarakannya di akhir bab ini. )

Fret adalah interaksi suara musik yang menyenangkan untuk didengar, ditentukan oleh ketergantungan suara tidak stabil pada yang stabil, dan pertama-tama pada suara stabil utama - tonik, dan memiliki karakter suara tertentu - kecenderungan. Sejarah budaya musik tahu banyak mode karakteristik orang yang berbeda dan waktu yang berbeda. Orang-orang Yunani kuno tahu tentang selusin fret, dan fret dari beberapa negara timur dan India sangat kompleks, aneh dan tidak biasa untuk pendengaran orang Eropa. Mode modern yang paling umum terdiri dari tujuh langkah utama, yang masing-masing dapat menambah atau mengurangi, yang memberikan lima suara tambahan. Jadi, fret gamma diatonik (7 langkah) berubah menjadi berwarna (12 suara). Langkah pertama dari fret adalah tonik. Hukum struktur fret adalah seluruh sains, landasan musikologi, dan banyak ilmuwan dan komposer telah mencurahkan seluruh hidup mereka untuk mempelajari hukum-hukum ini.

Kami terutama akan tertarik pada hukum matematika yang menggambarkan struktur fret, yaitu, sistem musik. Sistem musik adalah ekspresi matematis dari sistem hubungan pitch tertentu. Selain minat teoretis murni, sistem ini menemukan aplikasi dalam menyetel alat musik dengan nada suara yang tetap, seperti piano atau organ.

Sebagai kesimpulan, kami mencatat bahwa percobaan kami dengan menekan tombol pada piano dapat diakhiri dengan fenomena paling langka dan paling menyenangkan, ketika sistem suara yang diambil tidak hanya menjadi bagian dari fret, tetapi juga akan bermakna. Serangkaian bunyi berurutan artistik yang bermakna seperti itu dari ketinggian yang berbeda disebut melodi . Ini adalah apa yang kita suka bersenandung tergantung pada suasana hati kita - segar, sedih, ceria ...

Setelah kunjungan singkat ke musikologi teoretis, kita dapat kembali ke pantai Hellas yang cerah selama masa Pythagoras yang bijaksana. Kami akan mencoba mengembalikan alasan Pythagoras dan murid-muridnya ketika membangun sistem Pythagoras, karena sistem inilah yang menentukan selama ribuan tahun, jika tidak selamanya, seluruh pengembangan budaya musik, tidak hanya Eropa, tetapi juga Timur. Pythagoras sendiri tidak meninggalkan karya tulis apa pun, dan peninggalan orang-orang Pythagoras tampaknya merupakan tumpukan reruntuhan yang tak berpengharapan, mis., Kumpulan fragmen-fragmen yang secara tidak sengaja selamat dan kutipan selanjutnya. Tidak diragukan lagi, reruntuhan ini indah dan masih memukau imajinasi, seperti reruntuhan Parthenon yang terkenal, tetapi banyak dari fragmen-fragmen ini benar-benar hilang dan Anda sering hanya bisa menebak keseluruhannya. Namun ...

Monochord - single-string - adalah salah satu alat musik pertama orang Yunani kuno. Itu adalah sebuah kotak panjang yang dibutuhkan untuk memperkuat suara yang ditarik oleh tali. Dari bawah, tali ditarik oleh dudukan ponsel untuk membagi tali menjadi dua bagian yang terdengar terpisah. Pada kotak kayu di bawah tali ada skala divisi, yang memungkinkan untuk secara akurat menentukan bagian mana dari suara tersebut. Tentu saja, sebagai alat musik, monokord bagi kita akan tampak terlalu primitif, tetapi itu adalah instrumen fisik yang sangat baik dan alat pengajaran di mana para kontemplator kuno memahami kebijaksanaan literasi musik.

Orang-orang kuno menegaskan bahwa Pythagoras sudah mengetahui hukum getaran dari tali monochord dan konstruksi konsonan musik (konsonan), namun, kami menemukan catatan hukum ini dari Pythagoras Archite of Tarentus (428-365 SM), yang hidup satu setengah abad lebih lambat dari Pythagoras. . Arsitek itu, tentu saja, perwakilan paling menonjol dari sekolah Pythagoras, seorang teman filsuf Plato dan seorang guru matematika Eudoxus (sekitar 408 - 355 SM), seorang negarawan dan komandan. Fleksibilitas Architus luar biasa: ia memecahkan masalah de los yang terkenal dengan menggandakan kubus, dianggap sebagai ahli teori musik Pythagoras terbesar, yang pertama untuk merampingkan mekanika berdasarkan matematika dan mengurangi pergerakan mekanisme ke gambar geometris, bekerja pada model kayu merpati terbang. Menurut Van der Waerden, Arch adalah penulis buku VIII "The Beginnings" dari Euclid, yang menjabarkan teori proporsi aritmatika. Sebagai negarawan, Archit sangat dihormati: ia terpilih sebagai ahli strategi tujuh tahun berturut-turut ^* , meskipun menurut hukum, ahli strategi dipilih hanya untuk satu tahun. Melalui manuver diplomatik yang terampil, Archit menyelamatkan Plato dari tahanan dan dengan demikian menyelamatkan nyawa filsuf besar. "Arsitek Agung, daratan, dan lautan, dan kalkulator pasir ..." - tulis Horace.

* ( Ahli strategi - di negara-kota Yunani kuno, seorang pemimpin militer diberkahi dengan kekuatan militer dan politik Shi-ki. )

"Hukum Pythagoras-Archite", yang mendasari seluruh teori musik Pythagoras, dapat dirumuskan sebagai berikut:

1- Pitch (frekuensi osilasi f) dari string yang terdengar berbanding terbalik dengan panjangnya l:

(6.2)

di sini a adalah koefisien proporsionalitas, tergantung pada sifat fisik tali (ketebalan, bahan, dll.).

2. Dua string yang terdengar memberikan konsonan hanya ketika panjangnya disebut sebagai bilangan bulat yang membentuk angka segitiga 10 = 1 + 2 + 3 + 4, yaitu 1: 2, 2: 3, 3: 4.

Interval ini adalah "konsonan sempurna", dan koefisien intervalnya kemudian diberi nama Latin ^* :

^* ( Nama interval dalam musik adalah angka Latin, yang menunjukkan nomor seri skala skala yang membentuk interval dengan tahap awal: oktaf - kedelapan, kelima - kelima, keempat - keempat, dll. )

oktaf

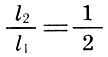
quint

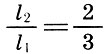
liter

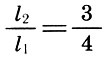
Bilangan segitiga 10

Juga dicatat bahwa fusi nada paling lengkap diberikan oleh satu oktaf (2/1), diikuti oleh quint (3/2) dan quart (4/3), yaitu semakin kecil angka n dalam kaitannya dengan bentuk 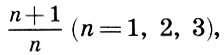semakin konsonan intervalnya.

"Hukum kedua Pythagoras - Archite" dan sekarang tampaknya mengejutkan. Apa yang bisa kita katakan tentang orang-orang Pythagoras, yang sangat dia kagumi! Di sini mereka menemukan konfirmasi dari seluruh filosofi mereka: bilangan bulat, apalagi, angka tetraktis mengatur segalanya, bahkan musik! Orang Pythagoras tidak membiarkan diri mereka menunggu lama dan memperpanjang hukum hubungan musik sedapat mungkin, termasuk struktur alam semesta.

Jadi, jika kita mengambil segmen l sama dengan 1/12 dari panjang string monochord l ₁ sebagai harga untuk membagi skala monochord, maka bersama-sama dengan seluruh string monochord panjang l ₁ = 12l bagian-bagiannya panjang l ₂ = 6l akan konsonan - suara adalah satu oktaf lebih tinggi (l ₂ / l ₁ = l / 2), l ₃ = 9l - terdengar quint lebih tinggi (l ₃ / l ₁ = 2/3) dan l ₄ = 8l - terdengar quart lebih tinggi (l ₄ / l ₁ = 3/4 ) Kesesuaian ini dan angka-angka yang menentukan 6, 8, 9, 12 disebut tetrad (empat). Orang-orang Pythagoras percaya bahwa tetrad adalah "skala yang sesuai dengan mana sirene bernyanyi." Ketika menyetel kecapi kuno, yang menjadi simbol musik, empat senarnya harus disetel sesuai dengan aturan tetrad, dan penyetelan senar yang tersisa tergantung pada fret untuk memainkannya.

Tetapi bagi pemikir kuno itu tidak cukup untuk menetapkan nilai numerik dari jumlah yang dipelajari. Mata dan pikiran Pythagoras terbiasa tidak hanya untuk mengukur, tetapi juga untuk mengukur, yaitu untuk mengungkapkan hubungan internal antara subyek yang diteliti, dengan kata lain, untuk membangun hubungan proporsional. Arsiteknya adalah seorang Pythagoras sejati, dan ia membangun hubungan proporsional antara konsonan sempurna utama - satu oktaf, kelima, dan keempat. Keputusan ini diperoleh Arsitek sehubungan dengan keinginan untuk membagi oktaf ke dalam interval yang harmonis. Mungkin, Arch didasarkan pada asumsi yang secara intuitif jelas bahwa, bersama dengan nada f ₁ dan f ₂ = 2f ₁ , memberikan konsonan utama - satu oktaf, konsonan dan aritmatika mereka berarti f ₃ = (f ₁ + f ₂ ) / 2 harus memberi. Tetapi kemudian panjang string l ₃ akan diekspresikan dalam bentuk panjang string l ₁ dan l ₂ sesuai dengan (6.2) sebagai berikut:

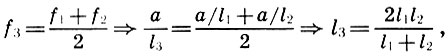
yaitu, l ₃ adalah rata-rata harmonik l ₁ dan l ₂ (lihat 5.1). Sebaliknya juga mudah dideteksi: rata-rata harmonik untuk frekuensi f1 dan f2 masuk ke rata-rata aritmatika untuk panjang l ₁ dan l ₂ :

Mengingat itu 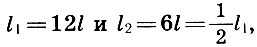Bersama dengan Arsitek, kami sampai pada kesimpulan penting:

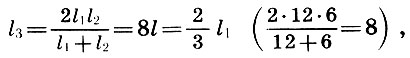
(6.3)


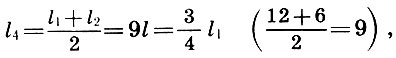
(6.4)

yaitu, yang kelima adalah rata-rata harmonik dari panjang string dari nada dasar l ₁ dan oktaf l ₂ , dan quart adalah rata-rata aritmatika dari l ₁ dan l ₂ .

Tetapi produk dari rata-rata aritmatika dan harmonik sama dengan produk dari angka asli:

(6.5)

dimana, membagi kedua bagian dengan l1 ² , kita memperoleh kesimpulan penting kedua:

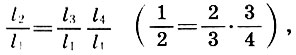
(6.6)

atau

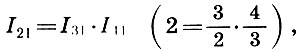
yaitu, satu oktaf adalah produk dari seperlima hingga satu liter.

Membagi (6,5) dengan l ₁ l ₃ , Archite mendapat sepertiga dari proporsi utama - geometris:

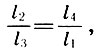
(6.7)

yang disebut "musikal": satu oktaf berhubungan dengan quint sebanyak satu liter dengan nada dasar .

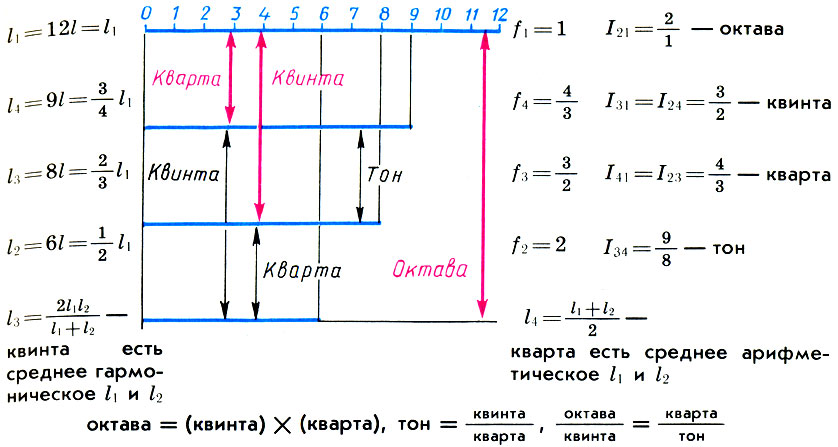
Pembagian string monochord (l1) menjadi bagian-bagian yang membentuk konsonan sempurna dengannya: satu oktaf (l2), kelima (l3) dan satu liter (l4) dan hubungan di antara mereka. Interval bahwa seluruh string bentuk monochord dengan bagian-bagiannya ditunjukkan oleh panah merah

Mudah untuk mendapatkan dua hubungan lagi:

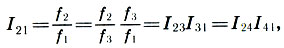
(6.8)

yaitu, oktaf dibagi menjadi dua interval konsonan yang tidak sama - kelima dan keempat . Interval yang memperpanjang interval ini ke satu oktaf disebut inversinya . Dengan demikian, quint adalah kebalikan dari quart dan sebaliknya.

Akhirnya, kami menemukan koefisien interval antara string dari kuinte l ₃ dan quart l ₄ , yang bersama-sama dengan intervalnya disebut nada (jangan membingungkan interval nada dan suara nada dari ketinggian tertentu):

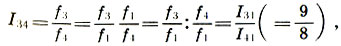
(6.9)

yaitu, interval nada sama dengan rasio dari kelima ke keempat .

Perhatikan bahwa, berbeda dengan jarak biasa pada garis lurus r ₂₁ = x ₂ - x _{1 yang} didefinisikan sebagai perbedaan antara koordinat akhir dan awal, koefisien interval - jarak ketinggian - didefinisikan sebagai rasio dari nada konstituennya. 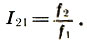Kemudian tiga nada f1 <f ₂ <f ₃ terletak pada jarak yang sama r dan membentuk deret aritmatika x ₁ , x ₂ = x ₁ + r, x ₃ = x ₁ + 2r. Oleh karena itu, koefisien interval ditambahkan dan dikurangi "secara geometris", dan intervalnya sendiri - "secara hitung", seperti jarak biasa, yaitu:

jumlah dari dua interval sama dengan produk dari koefisien interval mereka:

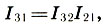
(6.10)

perbedaan dua interval sama dengan hasil bagi koefisien intervalnya:

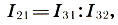
(6.11)

membagi interval menjadi n bagian yang sama berarti mengekstraksi akar derajat n dari koefisien intervalnya:

(6.12)

dll.

Untuk beralih dari koefisien interval ke interval jarak, cukup untuk memperkenalkan interval logaritmik L = log _a I dan frekuensi logaritmik F = log _a f. Kemudian, logaritma definisi (6.1) dan persamaan (6.10) - (6.12) kita mendapatkan definisi dan aturan aksi biasa dengan jarak:

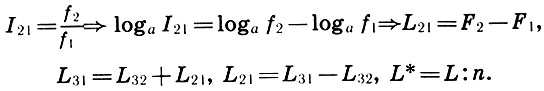
(6.13)

Solusi masalah divisi oktaf mendorong Archit segera dua bukti irasionalitas . Bahkan, jika kita mencoba untuk membagi oktaf menjadi dua interval I yang sama, maka, masukkan (6,8) I ₂₃ = I ₃₁ = I, kita memiliki

Tetapi dengan rasio panjang tali ini, disonansi yang jelas terdengar. Karena konsonan ditentukan oleh rasio bilangan bulat dari bentuk (n +1): 2, idenya menunjukkan bahwa bilangan tidak dapat dinyatakan oleh rasio dua bilangan bulat, yaitu, itu tidak rasional.

Bukti kedua irasionalitas kurang musikal, tetapi lebih matematis. Untuk menemukan akar kuadrat dari angka yang bukan kuadrat penuh, Archit menguraikannya menjadi dua faktor yang tidak sama (2 = 1 * 2), kemudian membentuk rata-rata aritmatika 3/2 dan rata-rata harmonik 4/3 dari faktor-faktor ini dan menyusun proporsi musik dari angka-angka ini ( 6.7):

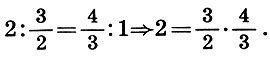
Produk dari istilah tengah proporsi ini sama dengan angka 2, dan perbedaannya kurang dari perbedaan perkiraan nol 2 - 1 = 1. Oleh karena itu, dapat dianggap sebagai nilai perkiraan .

(3/2 dengan kelebihan, 4/3 dengan kekurangan].

Setelah melakukan prosedur yang sama pada pendekatan pertama, kami memperoleh perkiraan kedua:

apalagi

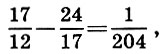
dan kemudian perkiraan ketiga:

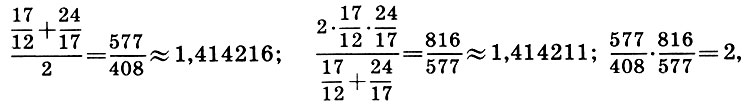
apalagi

1.414216-1.414211 = 0.000005.

Karena prosedur ini dapat diulang tanpa batas waktu, jelas jumlahnya irasional. Sepanjang jalan, kami yakin akan kebenaran gagasan Pythagoras bahwa semakin besar bilangan bulat dalam relasi, semakin akurat mereka mengekspresikan bilangan irasional (lihat hal. 96). Akhirnya, mengingat makna itu sama dengan 1,414213 ..., kita melihat bahwa metode "musikal" dari Archit menyatu dengan sangat cepat ke nilai yang tepat dan sudah perkiraan ketiga memberikan lima tempat desimal yang benar!

Tetapi kembali ke interval kita. Jadi, oktaf dibagi menjadi dua konsonan yang tidak sama dari kelima dan keempat, dan kelima - oleh keempat dan disonansi. Interval nada diambil sebagai interval antara suara tetangga (langkah) tingginya ketika membangun skala Pythagoras. Inilah kunci untuk membangun keresahan. Menurut ahli musik Soviet L. A. Mazel, interval kelima, dibagi menjadi satu liter dan nada, adalah elemen musik utama. Dengan memilih nada sebagai mode utama pembentukan, para ahli teori kuno hanya perlu mengesampingkan suara utama lalu nada lainnya 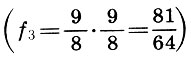dan sisa interval antara nada kedua dan nada quart 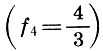hubungi halftone 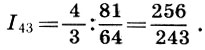Nama ini cukup dibenarkan, karena membagi interval nada menjadi setengah sesuai dengan rumus (6.12) berikan 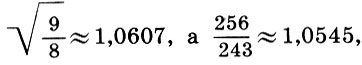mis., nada semi hampir sama dengan setengah nada ^* . Dengan demikian diperoleh dasar dari semua musik Yunani kuno - tetrachord - skala empat senar dalam satu liter.

^* ( Interval nada (halftone) dalam teori musik diterima sebagai unit pengukuran aritmatika interval, dan interval nada dan halftone, berbeda dengan koefisien interval mereka, disebut detik besar dan kecil. )

Jelas bahwa hanya ada tiga kemungkinan untuk posisi semitone di dalam tetrachord, yang menentukan sifat dan nama tetrachord:

Dorian: halftone - nada - nada;

Frigia: nada - semitone - nada;

Lidia: nada - nada - semitone .

Nama-nama tetrachords menunjukkan masing-masing wilayah Yunani dan Asia Kecil, yang masing-masing menyanyikan harmoni tersendiri.

Tentu saja, empat senar dalam satu liter tidak cukup untuk memimpin melodi, sehingga tetrachord terhubung. Kami telah menemukan bahwa satu oktaf terdiri dari dua liter dan satu nada; , , . , , «». «» — . :

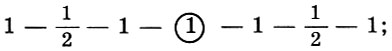
1 , 1/2 — , . . , , , (2 — , 3 — , - - - - - - c - o ), — ^* .

^* ( «» , (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) , — . )

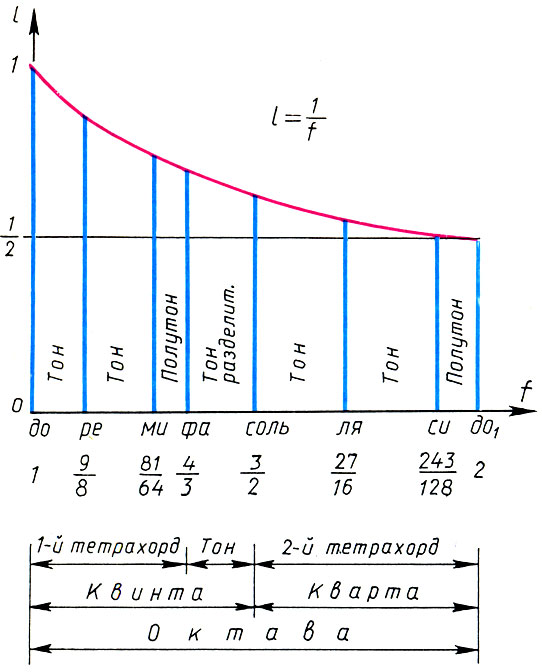Sistem Pythagoras dari Lydian gamut dan karakteristik matematikanya

, , , , , . . . f ₁ = 1, o : f ₁ = 1, f ₂ = ⁹ / ₈ , f ₃ = ⁹ / ₈ * ⁹ / ₈ = ⁸¹ / ₆₄ , f ₄ = ⁴ / ₃ . : f ₅ = ³ / ₂f _l = ³ / ₂ , f ₆ = ³ / ₂ f ₂ = ²⁷ / ₁₆ , f ₇ = ³ / ₂ f ₃ = ₂₄₃ / ₁₂₈ , f ₈ = ³ / ₂ f ₄ = 2. Akhirnya, kita miliki untuk koefisien selang

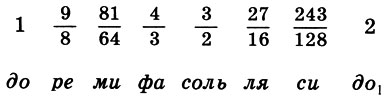(6.14)

Ini adalah kanon Pythagoras. Menurut legenda, kanon Pythagoras pertama kali menemukan aplikasi praktis dalam menyesuaikan kecapi Orpheus yang legendaris.

. «» , . . , -(-), — - (-). 6 , (- — — ) . , . , , . , , . 1 , , , , — , . .

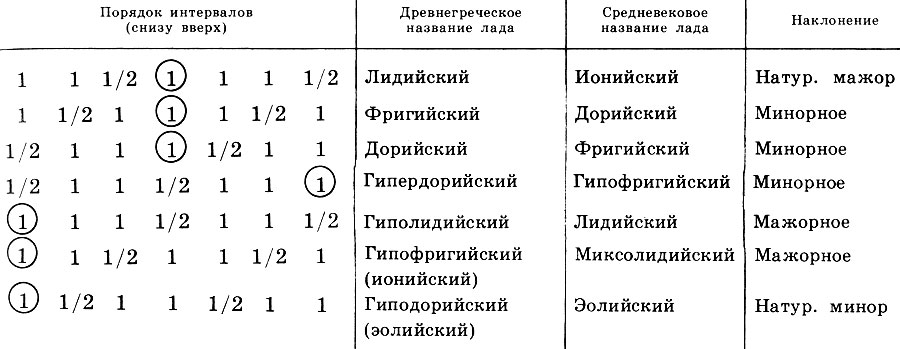Tabel 1. Urutan interval nada (1) dan semitone (1/2) dalam fret kuno (dari bawah ke atas), nama fret Yunani kuno dan abad pertengahan dan kecenderungannya

Jika kita ingat bahwa sekarang hanya dua fret yang mendominasi - besar dan kecil, kita hanya dapat bertanya-tanya seberapa canggih kesadaran musik kuno itu. Orang Yunani mengisi setiap jalan dengan konten etis dan estetika tertentu, "etos" -nya, membangun hubungan yang jelas antara gambar musik dan keadaan jiwa. Fungsi magis dan bahkan medis dikaitkan dengan musik, tetapi kepentingan khusus melekat pada musik sebagai sarana pendidikan.

Menari menari. Relief

, «» , . , , ,- (. 551-479 . . .), : « , — ». , , , . , , , , . , , , . , . , , . , , «» , , , , .

Aristoteles dalam Politics menilai fret, bahkan mungkin lebih keras daripada Plato, hanya mengakui mode Dorian sebagai mode yang mampu melatih jiwa. Namun demikian, Aristoteles membuat klasifikasi mode "etis" yang terperinci, mode yang membedakan yang menyebabkan keseimbangan mental (Dorian), sebaliknya, melanggarnya (mode hypofrigian - "table"), menggairahkan keinginan dan keinginan untuk bertindak (mode hypodorian dari tragedi Yunani), menyebabkan keadaan gembira dan gembira (Frigia, hipolidian).

Kami menemukan deskripsi yang indah tentang "etos" fret Yunani dalam buku penulis Romawi kuno Apuleius (sekitar 124 -?) "Florids": "Dulu ada pemain suling bernama Antigenides. Setiap suara dalam permainan musisi ini manis, semua fret sudah akrab baginya, dan dia bisa menciptakan kembali untuk Anda, sesuai pilihan Anda, kesederhanaan fret Aeolian, kekayaan Ionia, kesedihan Lydian, kegembiraan orang Frigia, dan militansi Doria. "

Namun, berhentilah! Apakah ada kontradiksi di sini? Suasana hati Dorian disebut berperang, tetapi nyatanya, pada kenyataannya, minor kita! Karena suasana hati Dorian yang dianggap benar-benar Yunani, ternyata karakter utama musik Yunani adalah sedih, kecil. Bagi orang-orang Yunani, suasana hati Dorian adalah ekspresi dari kegembiraan, keceriaan, dan bahkan militansi. Inilah bagaimana sarjana kontemporer kuno yang luar biasa, filsuf terakhir dari "zaman perak" Rusia, Profesor A. F. Losev (1893-1988) ^* menjelaskan: "Seni Yunani adalah penegasan hidup yang tidak berubah-ubah." Pengekangan diri yang mulia dan bahkan kesedihan tidak meninggalkan bahasa Yunani bahkan ketika dia sedang bersenang-senang, ketika dia dengan riang membangun hidupnya, ketika dia berperang dan sekarat. Frasa "riang" dengan satu atau lain cara condong ke arah duka yang indah, mulia, kuat, penting ini, dan pada saat yang sama sedih yang menyedihkan - Dorian. Suasana Dorian adalah gaya pahatan musik Yunani ... Jadi seluruh pahatan Yunani sangat bijaksana, sedih dan mulia. "

^* ( Nasib Aleksei Fedorovich Losev bahagia dan tragis. Ia bahagia karena sampai hari terakhir hidupnya yang ke-95, Losev mempertahankan kapasitas kerja yang luar biasa dan berhasil menyelesaikan pekerjaan utamanya - delapan volume "History of Ancient Aesthetics." Tragis, karena delapan volume karyanya ditulis setengah abad sebelumnya (1927 - 1930), mereka dibenci, dan penulis itu sendiri, yang secara ilegal ditekan, melanjutkan penelitian filosofisnya tentang pembangunan Terusan Laut-Baltik Putih, di mana ia menulis: “Aku dirantai ketika jiwaku bergolak kekuatan abadi dan tidak ada habisnya. "Salah satu karya Losev," Musik sebagai subjek logika, "dapat berfungsi sebagai cahaya penuntun untuk buku ini. Meskipun demikian, nasib A.F. Losev bahagia, karena manuskrip tidak terbakar. Hari ini, warisan filosofi agung A F. Losev mendapatkan kembali kelahirannya. )

Tetapi bagaimana dengan cara Lidia? Lagipula, ini tepatnya utama kami, sementara Apuleius menyebutnya sedih, dan Plato - pemakaman! Nah, dalam menilai fret Lidia, Aristoteles tidak setuju dengan Plato, menemukan kekanak-kanakan dan pesona naif di fret Lidia dan menghubungkannya dengan fret yang menyebabkan keseimbangan mental. Seiring waktu, mode Lydia telah kehilangan karakternya yang menyedihkan, dan para ahli teori kuno mulai lebih sering berbicara tentang "melodi Lydia yang manis" atau "melodi Lydia yang beragam."

Dengan demikian, kita melihat bahwa pertanyaan tentang "etos" fret tidak diselesaikan dengan jelas dan sebagian besar ditentukan oleh tradisi penerapan fret ini atau itu. Dan di zaman kita, pendengar, yang dibesarkan, misalnya, dalam musik India yang halus dan aneh, tidak membedakan antara mayor dan minor, belum lagi "etos" mereka. Tentu saja, suasana hati utama dibedakan oleh nada yang lebih ringan dan lebih menyenangkan, dan ada alasan obyektif untuk ini, yang akan kita bahas di bab 10. Tetapi realisasi kemungkinan ini tergantung pada sejumlah faktor lain (tempo, ritme, pola melodi, dll.), Dan karena itu ada banyak karya ceria, energik dalam minor dan sedih, merenung di mayor. Mari kita ingat setidaknya "Sonata yang Menyedihkan" di Beethoven minor , monolog Pahlawan yang bersemangat, yang menyerukan pertempuran sengit dan bahkan kematian. Banyak seniman mengambil banyak julukan untuk sonata ini (walaupun, mungkin, yang terbaik dari mereka - menyedihkan - milik Beethoven sendiri), tetapi tidak dapat disebut sedih saja - kecil. Sebaliknya, Nocturne No. 2 Op. Flat utama ke-9 dari Chopin diresapi dengan suasana lamunan yang lembut. Ini adalah kenangan sedih yang kabur dari penulis, tetapi tidak berarti permainan yang ceria. Sebagai kesimpulan, mari kita coba mengatakan beberapa kata tentang "etos interval", karena bab ini dikhususkan untuk analisis interval musik. Kami akan mencoba, karena masalah ini bahkan lebih kontroversial dan tidak berkembang daripada "etos fret." Namun ...

Sejauh ini, kita belum mengatakan apa-apa tentang "konsonan paling sempurna" - prima (serempak) (l ₂ / l ₁ = 1, yaitu, dua string menghasilkan suara dengan ketinggian yang sama), karena dari sudut pandang matematika, interval ini tidak menarik. Namun, dalam orkestra, interval paling sederhana ini memainkan peran besar, memberikan volume dan kecerahan suara ini.

Konsonan sempurna berikutnya adalah oktaf. Pada saat yang sama, oktaf juga memberi kesan suara tiga dimensi, dan dengan suara berurutan, perasaan luas dan luas. Ilustrasi yang sangat baik tentang hal ini adalah "Song of the Motherland" oleh komposer I. O. Dunaevsky (1900-1955). Dalam paduan suara ("Dari Moskow ke pinggiran ..."), satu oktaf naik (l ₁ / l ₂ = 2) terdengar dua kali, melukis hamparan luas dari Tanah Air kita. Di sini, setelah dua oktaf, ada kelima naik. Quinta (l ₁ / l ₂ = 3/2) juga terdengar lebar, tetapi lebih bertekstur dan dinamis daripada satu oktaf.

Melodi dari banyak lagu dan nyanyian revolusioner dimulai dengan selang waktu satu liter naik (l ₁ / l ₂ = 4/3), misalnya, Internasional, Lagu Kebangsaan Uni Soviet, Marseillaise. Di sini, interval liter terdengar dengan tegas dan aktif, seperti ajakan untuk bertindak.

Ada "etos" khusus dalam interval satu detik: dengan suara simultan, itu tidak harmonis dan tidak menyenangkan, tetapi dengan suara berturut-turut yang sebelumnya meluap ke yang berikutnya, membentuk aliran alami melodi dari satu suara ke suara lainnya. Dalam sebuah melodi, interval antara dua suara referensi sering diisi dengan interval kedua berturut-turut. Sebagai contoh, lagu "A Birch Stood in the Field" dimulai dengan interval kelima yang diisi dengan detik berturut-turut, yang memberikan kesan aliran melodi yang tenang dan megah, seperti gambar megah dan tenang dari alam Rusia.

Dan yang paling tidak menyenangkan dan disonan adalah interval triton atau semi-oktaf (l ₁ / l ₂ = ) Dengan ketidakkonsistenannya, interval ini "mendorong" Archite ke "bukti musik" irasionalitas .

Terima kasih kepada Perpustakaan Matematika untuk mendigitalkan buku ini.