Richard Hamming: Bab 10. Teori Pengkodean - I

"Tujuan kursus ini adalah untuk mempersiapkan Anda untuk masa depan teknis Anda."

Hai, Habr. Ingat artikel yang luar biasa "Anda dan Pekerjaan Anda" (+219, 2442 bookmark, 394k dibaca)?

Jadi Hamming (ya, ya, memeriksa sendiri dan memperbaiki kode Hamming ) memiliki seluruh buku yang ditulis berdasarkan ceramahnya. Kami menerjemahkannya, karena lelaki itu berbicara bisnis.

Buku ini bukan hanya tentang IT, itu adalah buku tentang gaya berpikir orang yang sangat keren. “Ini bukan hanya muatan pemikiran positif; itu menggambarkan kondisi yang meningkatkan peluang melakukan pekerjaan dengan baik. ”

Kami telah menerjemahkan 28 (dari 30) bab. Dan kami sedang mengerjakan edisi kertas.

Teori Pengkodean - I

Setelah mempertimbangkan komputer dan prinsip kerja mereka, kami sekarang akan mempertimbangkan masalah informasi: bagaimana komputer mewakili informasi yang ingin kami proses. Makna karakter apa pun mungkin tergantung pada bagaimana ia diproses, mesin tidak memiliki arti khusus untuk bit yang digunakan. Ketika membahas sejarah perangkat lunak, Bab 4, kami mempertimbangkan beberapa bahasa pemrograman sintetis, di mana kode instruksi istirahat bertepatan dengan kode instruksi lainnya. Situasi ini tipikal untuk sebagian besar bahasa, makna instruksi ditentukan oleh program yang sesuai.

Untuk menyederhanakan masalah penyajian informasi, kami mempertimbangkan masalah pengiriman informasi dari titik ke titik. Pertanyaan ini terkait dengan masalah informasi konservasi. Masalah dalam mengirimkan informasi dalam ruang dan waktu adalah identik. Gambar 10.1 menunjukkan model standar untuk mengirimkan informasi.



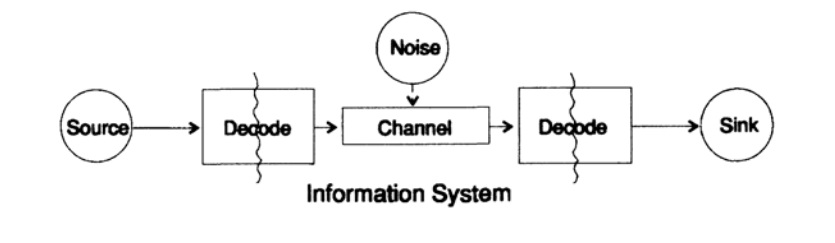Gambar 10.1

Di sebelah kiri dalam gambar 10.1 adalah sumber informasi. Saat mempertimbangkan model, kami tidak peduli tentang sifat sumbernya. Ini dapat berupa seperangkat simbol alfabet, angka, rumus matematika, not musik, simbol yang dengannya kita dapat mewakili gerakan dansa - sifat sumber dan makna simbol yang tersimpan di dalamnya bukan bagian dari model transmisi. Kami hanya mempertimbangkan sumber informasi, dengan batasan seperti itu kami memperoleh teori umum yang kuat yang dapat diperluas ke banyak bidang. Ini adalah abstraksi dari banyak aplikasi.

Ketika Shannon menciptakan teori informasi pada akhir 1940-an, diyakini bahwa itu harus disebut teori komunikasi, tetapi ia bersikeras pada istilah informasi. Istilah ini telah menjadi penyebab konstan dari meningkatnya minat dan kekecewaan terus menerus dalam teori. Penyelidik ingin membangun "teori informasi" keseluruhan, mereka merosot menjadi teori serangkaian karakter. Kembali ke model transmisi, kami memiliki sumber data yang perlu dikodekan untuk transmisi.

Encoder terdiri dari dua bagian, bagian pertama disebut source encoder, nama yang tepat tergantung pada jenis sumber. Sumber dari berbagai jenis data berhubungan dengan berbagai jenis penyandi.

Bagian kedua dari proses pengkodean disebut pengkodean saluran dan tergantung pada jenis saluran untuk mentransmisikan data. Dengan demikian, bagian kedua dari proses pengkodean konsisten dengan jenis saluran transmisi. Jadi, ketika menggunakan antarmuka standar, data dari sumber awalnya disandikan sesuai dengan persyaratan antarmuka, dan kemudian sesuai dengan persyaratan saluran data yang digunakan.

Menurut model, pada Gambar 10.1, saluran data terkena "noise acak tambahan". Semua kebisingan dalam sistem digabungkan pada saat ini. Diasumsikan bahwa encoder menerima semua karakter tanpa distorsi, dan decoder menjalankan fungsinya tanpa kesalahan. Ini adalah beberapa idealisasi, tetapi untuk banyak tujuan praktis itu dekat dengan kenyataan.

Tahap decoding juga terdiri dari dua tahap: saluran - standar, standar - penerima data. Pada akhir transfer data ditransmisikan ke konsumen. Dan lagi, kami tidak mempertimbangkan bagaimana konsumen menginterpretasikan data ini.

Seperti disebutkan sebelumnya, sistem transmisi data, misalnya, pesan telepon, radio, program TV, menyajikan data dalam bentuk sekumpulan angka dalam register komputer. Saya ulangi lagi, transmisi dalam ruang tidak berbeda dengan transmisi dalam waktu atau menyimpan informasi. Apakah Anda memiliki informasi yang akan diperlukan setelah beberapa saat, maka harus dikodekan dan disimpan pada sumber penyimpanan data. Jika perlu, informasi diterjemahkan. Jika sistem pengkodean dan penguraiannya sama, kami mengirimkan data melalui saluran transmisi tanpa perubahan.

Perbedaan mendasar antara teori yang disajikan dan teori biasa dalam fisika adalah asumsi bahwa tidak ada noise pada sumber dan penerima. Bahkan, kesalahan terjadi pada peralatan apa pun. Dalam mekanika kuantum, kebisingan terjadi pada setiap tahap sesuai dengan prinsip ketidakpastian, dan bukan sebagai kondisi awal; dalam kasus apa pun, konsep kebisingan dalam teori informasi tidak setara dengan konsep serupa dalam mekanika kuantum.
Untuk definiteness, kami akan mempertimbangkan bentuk biner dari representasi data dalam sistem. Formulir lain diproses dengan cara yang sama, untuk kesederhanaan kami tidak akan mempertimbangkannya.

Kita mulai dengan pertimbangan sistem dengan karakter yang dikodekan dengan panjang variabel, seperti dalam kode titik dan garis Morse klasik, di mana karakter yang sering muncul pendek dan jarang ada yang panjang. Pendekatan ini memungkinkan Anda untuk mencapai efisiensi kode tinggi, tetapi perlu dicatat bahwa kode Morse adalah ternary, bukan biner, karena berisi ruang antara titik dan garis. Jika semua karakter dalam kode memiliki panjang yang sama, maka kode tersebut disebut kode blok.

Properti pertama yang diperlukan dari kode adalah kemampuan untuk secara unik men-decode pesan tanpa adanya noise, setidaknya ini tampaknya properti yang diinginkan, walaupun dalam beberapa situasi persyaratan ini dapat diabaikan. Data dari saluran transmisi untuk penerima terlihat seperti aliran karakter dari nol dan satu.

Kami akan memanggil dua karakter yang berdekatan ekstensi ganda, tiga karakter yang berdekatan ekstensi tiga, dan dalam kasus umum, jika kita meneruskan karakter N, penerima melihat penambahan pada kode dasar karakter N. Penerima, yang tidak mengetahui nilai N, harus membagi aliran menjadi blok siaran. Atau, dengan kata lain, penerima harus dapat menguraikan aliran secara unik untuk mengembalikan pesan aslinya.

Pertimbangkan alfabet dari sejumlah kecil karakter, biasanya huruf jauh lebih besar. Abjad bahasa mulai dari 16 hingga 36 karakter, termasuk karakter huruf besar dan kecil, tanda angka, tanda baca. Misalnya, dalam tabel ASCII 128 = 2 ^ 7 karakter.
Pertimbangkan kode khusus yang terdiri dari 4 karakter s1, s2, s3, s4

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

Bagaimana seharusnya penerima menerjemahkan ungkapan yang diterima berikutnya

0011 ?

Bagaimana s1s1s4 atau bagaimana s2s4 ?

Anda tidak dapat memberikan jawaban yang jelas untuk pertanyaan ini, kode ini pasti tidak diterjemahkan, oleh karena itu, tidak memuaskan. Kode, di sisi lain

s1 = 0; s2 = 10; s3 = 110; s4 = 111

menerjemahkan pesan dengan cara yang unik. Ambil string acak dan pertimbangkan bagaimana penerima akan menerjemahkannya. Anda perlu membangun pohon decoding Menurut formulir pada Gambar 10.II. Tali

1101000010011011100010100110 ...

dapat dipecah menjadi blok-blok karakter

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110, ...

sesuai dengan aturan berikut untuk membangun pohon decoding:

Jika Anda berada di atas pohon, baca karakter berikutnya. Saat Anda mencapai daun pohon, Anda mengonversi urutan ke karakter dan kembali ke awal.

Alasan keberadaan pohon seperti itu adalah bahwa tidak ada karakter yang merupakan awalan dari yang lain, jadi Anda selalu tahu kapan Anda harus kembali ke awal pohon decoding.

Perlu memperhatikan hal-hal berikut. Pertama, decoding adalah proses aliran ketat, di mana setiap bit diperiksa hanya sekali. Kedua, protokol biasanya menyertakan karakter yang merupakan penanda akhir dari proses decoding dan diperlukan untuk menunjukkan akhir pesan.

Kegagalan menggunakan karakter trailing adalah kesalahan umum dalam desain kode. Tentu saja, Anda dapat memberikan mode decoding konstan, dalam hal ini karakter trailing tidak diperlukan.



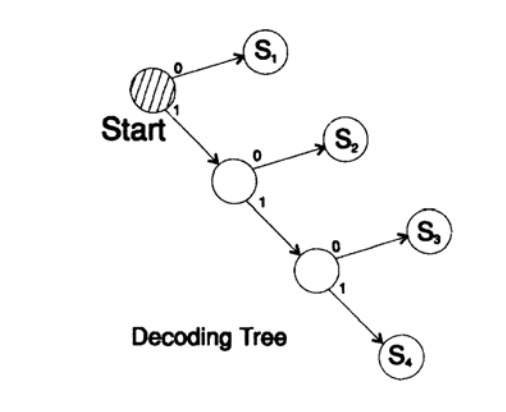Gambar 10.II

Pertanyaan selanjutnya adalah kode untuk stream (instan) decoding. Pertimbangkan kode yang diperoleh dari yang sebelumnya dengan menampilkan karakter

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Misalkan kita mendapatkan urutan 011111 ... 111 . Satu-satunya cara Anda dapat mendekode teks pesan adalah dengan mengelompokkan bit dari akhir 3 ke dalam grup dan memilih grup dengan nol di depannya, setelah itu Anda dapat mendekode. Kode semacam itu diterjemahkan dengan cara yang unik, tetapi tidak secara instan! Untuk decoding, Anda harus menunggu akhir transfer! Dalam prakteknya, pendekatan ini menghilangkan laju decoding (teorema Macmillan), oleh karena itu, perlu untuk mencari metode decoding instan.

Pertimbangkan dua cara untuk menyandikan karakter yang sama, Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

Pohon decoding dari metode ini ditunjukkan pada 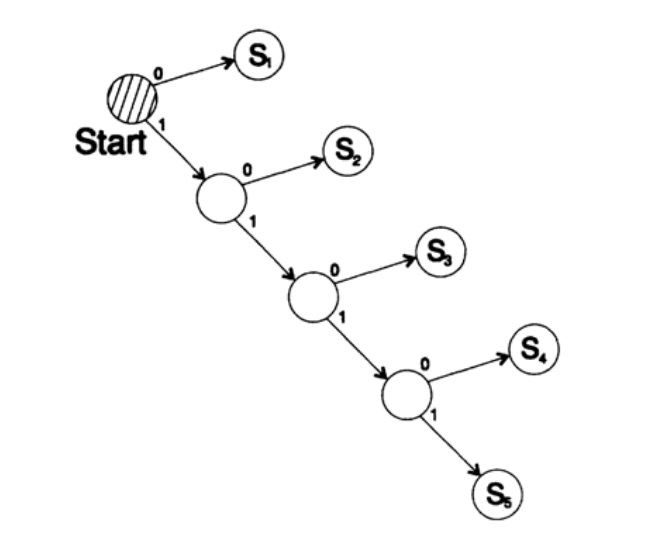Gambar 10.III.



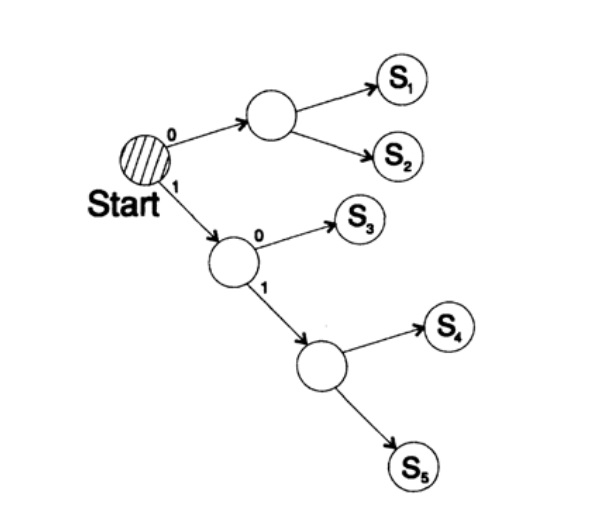
Gambar 10.III

Cara kedua

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111 ,

Pohon decoding dari perawatan ini ditunjukkan pada Gambar 10.IV.

Cara paling jelas untuk mengukur kualitas kode adalah panjang rata-rata untuk satu set pesan. Untuk ini, perlu untuk menghitung panjang kode setiap karakter dikalikan dengan probabilitas kemunculan pi yang sesuai. Dengan demikian, panjang seluruh kode diperoleh. Rumus untuk panjang rata-rata L dari kode untuk alfabet karakter q adalah sebagai berikut



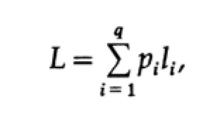
di mana pi adalah probabilitas kemunculan simbol si, li adalah panjang yang sesuai dari simbol yang dikodekan. Untuk kode efisien, nilai L harus sekecil mungkin. Jika P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 dan p5 = 1/16, maka untuk kode # 1 kita mendapatkan nilai panjang kode



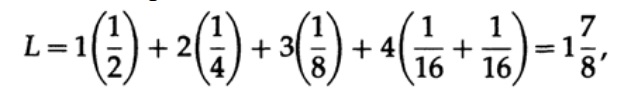
Dan untuk kode # 2



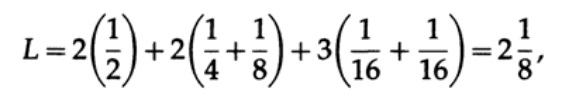
Nilai yang diperoleh menunjukkan preferensi kode pertama.
Jika semua kata dalam alfabet memiliki probabilitas kejadian yang sama, maka kode kedua akan lebih disukai. Misalnya, dengan pi = 1/5, panjang kode # 1



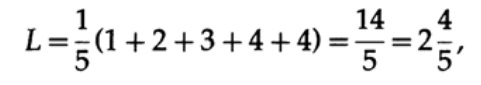
dan panjang kode # 2



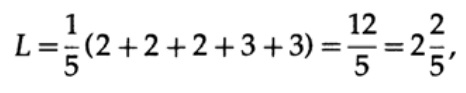
hasil ini menunjukkan preferensi untuk 2 kode. Jadi, ketika mengembangkan kode "baik", perlu untuk mempertimbangkan kemungkinan kemunculan karakter.



Gambar 10.IV



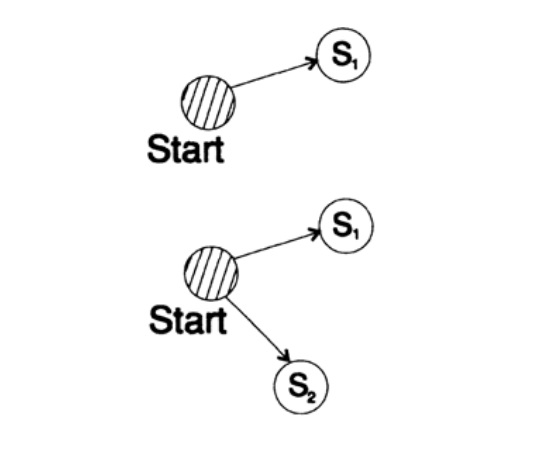Gambar 10.V

Pertimbangkan ketidaksetaraan Kraft, yang menentukan nilai batas panjang kode simbol li. Dalam basis 2, ketidaksetaraan direpresentasikan sebagai



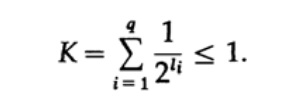
Ketidaksetaraan ini menunjukkan bahwa alfabet tidak dapat memiliki terlalu banyak karakter pendek, jika tidak, jumlahnya akan cukup besar.

Untuk membuktikan ketidaksetaraan Kraft untuk setiap kode pendek unik yang didekodekan, kami membuat pohon pendekodean dan menerapkan metode induksi matematika. Jika pohon memiliki satu atau dua daun, seperti yang ditunjukkan pada Gambar 10.V, maka ketidaksetaraan itu benar. Selanjutnya, jika pohon itu memiliki lebih dari dua daun, maka kita membelah pohon panjang m menjadi dua sub pohon. Menurut prinsip induksi, kita mengasumsikan bahwa ketidaksetaraan berlaku untuk setiap cabang dengan tinggi m -1 atau kurang. Menurut prinsip induksi, menerapkan ketimpangan untuk setiap cabang. Nyatakan panjang kode cabang K 'dan K' '. Ketika menggabungkan dua cabang pohon, panjang masing-masing bertambah sebesar 1, oleh karena itu, panjang kode terdiri dari jumlah K '/ 2 dan K' '/ 2,



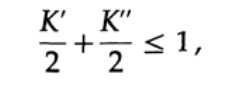
teorema terbukti.

Pertimbangkan bukti teorema Macmillan. Kami menerapkan ketidaksetaraan Kraft ke kode decode tanpa thread. Buktinya didasarkan pada fakta bahwa untuk bilangan K> 1, kekuatan n dari bilangan jelas lebih dari fungsi linier n, di mana n adalah bilangan yang agak besar. Kami meningkatkan ketimpangan Kraft ke kekuatan ke-n dan menyajikan ekspresi sebagai jumlah



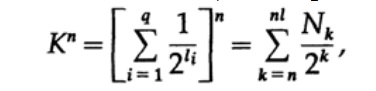
di mana Nk adalah jumlah karakter dari panjang k, penjumlahan dimulai dengan panjang minimum dari representasi n dari karakter dan berakhir dengan panjang maksimum nl, di mana l adalah panjang maksimum dari karakter yang dikodekan. Dari persyaratan unik decoding maka ikuti itu. Jumlahnya disajikan sebagai



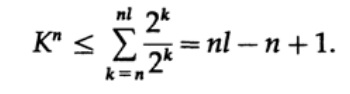
Jika K> 1, maka perlu untuk menetapkan n cukup besar agar ketidaksetaraan menjadi salah. Oleh karena itu, k <= 1; Teorema Macmillan terbukti.

Perhatikan beberapa contoh penerapan ketidaksetaraan Kraft. Bisakah kode yang diterjemahkan secara unik ada dengan panjang 1, 3, 3, 3? Ya sejak itu



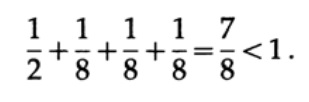
Bagaimana dengan panjang 1, 2, 2, 3? Hitung sesuai dengan rumus



Ketimpangan dilanggar! Terlalu banyak karakter pendek dalam kode ini.

Kode koma adalah kode yang terdiri dari karakter 1, diakhiri dengan karakter 0, dengan pengecualian karakter terakhir yang terdiri dari semua. Salah satu kasus khusus adalah kode.

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5 = 11111.

Untuk kode ini, kami memperoleh ekspresi untuk ketidaksetaraan Kraft



Dalam hal ini, kami mencapai kesetaraan. Sangat mudah untuk melihat bahwa untuk kode titik, ketimpangan Kraft merosot menjadi kesetaraan.

Saat membuat kode, Anda harus memperhatikan jumlah Kraft. Jika jumlah Kraft mulai melebihi 1, maka ini merupakan sinyal tentang perlunya memasukkan karakter dengan panjang yang berbeda untuk mengurangi panjang kode rata-rata.

Perlu dicatat bahwa ketidaksetaraan Kraft tidak berarti bahwa kode ini dapat didekodekan secara unik, tetapi ada kode dengan karakter dengan panjang sedemikian yang secara unik diterjemahkan. Untuk membangun kode dekode yang unik, Anda dapat menetapkan panjang terkait dalam bit li dengan nomor biner. Misalnya, untuk panjang 2, 2, 3, 3, 4, 4, 4, 4, kita memperoleh ketimpangan Kraft



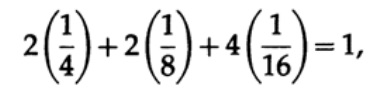
Oleh karena itu, kode aliran yang diterjemahkan seperti itu mungkin ada.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

Saya ingin memperhatikan apa yang sebenarnya terjadi ketika kita bertukar ide. Sebagai contoh, pada saat ini saya ingin mentransfer ide dari kepala saya ke milik Anda. Saya mengucapkan beberapa kata yang melaluinya, seperti yang saya yakini, Anda dapat memahami (mendapatkan) ide ini.

Tetapi ketika sedikit kemudian Anda ingin menyampaikan ide ini kepada teman Anda, Anda hampir pasti akan mengucapkan kata-kata yang sama sekali berbeda. Faktanya, makna atau makna tidak tertutup dalam kata-kata tertentu. Saya menggunakan beberapa kata, dan Anda dapat menggunakan kata-kata yang sangat berbeda untuk menyampaikan gagasan yang sama. Dengan demikian, kata-kata yang berbeda dapat menyampaikan informasi yang sama. Tetapi, segera setelah Anda memberi tahu lawan bicara Anda bahwa Anda tidak memahami pesan tersebut, maka sebagai patokan lawan bicara akan memilih serangkaian kata yang berbeda, yang kedua atau bahkan yang ketiga, untuk menyampaikan artinya. Dengan demikian, informasi tersebut tidak dilampirkan dalam serangkaian kata-kata tertentu. Segera setelah Anda menerima kata-kata ini atau itu, maka Anda melakukan banyak pekerjaan ketika menerjemahkan kata-kata itu ke dalam gagasan yang ingin disampaikan lawan bicara kepada Anda.

Kami belajar memilih kata-kata untuk beradaptasi dengan lawan bicara. Dalam arti tertentu, kami memilih kata-kata yang sesuai dengan pemikiran kami dan tingkat kebisingan di saluran, meskipun perbandingan seperti itu tidak secara akurat mencerminkan model yang saya gunakan untuk mewakili suara dalam proses pengodean ulang. Dalam organisasi besar, masalah serius adalah ketidakmampuan lawan bicara untuk mendengar apa yang dikatakan orang lain. Di posisi senior, karyawan mendengar apa yang "ingin mereka dengar". Dalam beberapa kasus, Anda perlu mengingat ini ketika Anda naik tangga karier. Penyajian informasi dalam bentuk formal adalah refleksi parsial dari proses dari kehidupan kita dan telah menemukan aplikasi luas jauh melampaui batas-batas aturan formal dalam aplikasi komputer.

Dilanjutkan ...

Siapa yang ingin membantu dengan terjemahan, tata letak, dan penerbitan buku - tulis dalam email pribadi atau email magisterludi2016@yandex.ru

Ngomong-ngomong, kami juga meluncurkan terjemahan buku keren lainnya - “Mesin Impian: Sejarah Revolusi Komputer” )