👨🏻‍🎨 👩🏿‍💻 🧗 Pengkode Otomatis dan Kecerdasan Buatan yang Kuat ⚔️ 🍲 👸🏾

Teori auto-encoders dan menghasilkan model baru-baru ini telah dikembangkan secara serius, tetapi beberapa karya dikhususkan untuk bagaimana menggunakannya dalam masalah pengenalan. Pada saat yang sama, properti autoencoder untuk memperoleh model data parametrik tersembunyi dan konsekuensi matematis dari ini memungkinkan untuk menghubungkannya dengan metode pengambilan keputusan Bayesian.

Artikel ini mengusulkan perangkat matematika asli "seperangkat auto-encoders dengan ruang laten umum", yang memungkinkan Anda untuk mengekstraksi konsep abstrak dari data input dan menunjukkan kemampuan untuk "pembelajaran sekali pakai". Selain itu, dapat digunakan untuk mengatasi banyak masalah mendasar dari algoritma pembelajaran mesin modern berdasarkan jaringan multilayer dan pendekatan "Pembelajaran mendalam".

Latar belakang

Jaringan saraf tiruan, dilatih menggunakan mekanisme back propagation of errors, hampir menggantikan pendekatan lain dalam banyak masalah pengenalan dan estimasi parameter. Tetapi mereka memiliki sejumlah kelemahan, yang, tampaknya, tidak dapat dihilangkan tanpa revisi serius terhadap pendekatan tersebut:

ketidakstabilan ekstrim untuk memasukkan data yang tidak ditemukan dalam sampel pelatihan (termasuk dalam kasus serangan permusuhan)
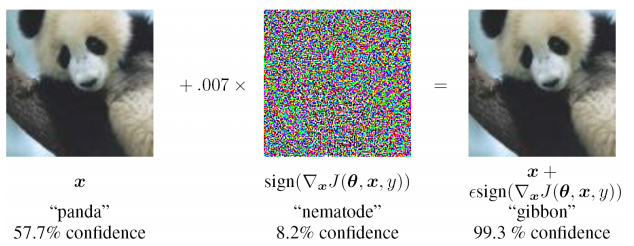
sulit untuk menilai sumber masalah dan melatih kembali secara lokal di salah satu level (Anda hanya perlu menambah sampel pelatihan dan melatih kembali), yaitu. masalah kotak hitam
kemungkinan interpretasi yang berbeda dari informasi input yang sama tidak disediakan, sifat statistik dari data yang diamati diabaikan

Terlibat dalam memecahkan masalah yang diterapkan, dan mengandalkan sejumlah pekerjaan yang ada, saya mengusulkan pendekatan yang terasa berbeda dari yang ada, menghilangkan sejumlah kekurangan mereka dan berlaku untuk memecahkan masalah yang diterapkan di berbagai bidang pembelajaran mesin.

Auto Encoder untuk Memperkirakan Kepadatan Distribusi

Dalam teori pengambilan keputusan, tempat yang sangat penting ditempati oleh kepadatan distribusi (atau fungsi distribusi) dari variabel acak. Diperlukan perkiraan fungsi distribusi untuk menghitung risiko posterior.

Ternyata encoders otomatis sangat alami untuk mengevaluasi fungsi distribusi. Ini dapat dijelaskan sebagai berikut: set data pelatihan ditentukan oleh kepadatan distribusinya. Semakin tinggi kepadatan contoh pelatihan di sekitar titik lokal di ruang input, semakin baik auto-encoder merekonstruksi vektor input di lokasi ini di ruang. Selain itu, di dalam autoencoder terdapat vektor representasi laten dari data input (biasanya berdimensi rendah), dan jika data diproyeksikan dalam ruang laten ke area yang sebelumnya tidak digunakan dalam pelatihan, maka tidak ada yang serupa dalam sampel pelatihan.

Ada sejumlah pekerjaan yang tertutup dan agak terisolasi:

Yang pertama membenarkan bahwa hasil rekonstruksi Denoising dari auto-encoders terkait dengan fungsi kepadatan probabilitas dari data input, tetapi sejumlah pembatasan dikenakan pada auto-encoders. Yang kedua berisi persyaratan yang cukup untuk enkoder otomatis - bobot enkoder dan dekoder harus "terhubung", mis. matriks bobot dari lapisan pembuat kode adalah matriks yang ditransposisikan dari pembuat kode. Dalam karya terakhir, kondisi yang diperlukan dan cukup untuk fakta bahwa auto encoder dikaitkan dengan kerapatan probabilitas lebih diselidiki sepenuhnya.

Karya-karya ini benar-benar memperkuat dasar teoritis untuk hubungan autoencoder dengan kepadatan distribusi data pelatihan. Dalam masalah terapan, analisis serius seperti itu sering kali tidak diperlukan, oleh karena itu, pendekatan yang sedikit berbeda akan diberikan di bawah ini yang akan memungkinkan kami untuk memperkirakan fungsi kepadatan probabilitas dari data input karena autoencoder yang sebelumnya terlatih.

Contoh MNIST

Dalam karya-karya yang bahkan lebih awal, ide empiris diusulkan bahwa untuk masalah klasifikasi dimungkinkan untuk melatih penyandi-otomatis dengan jumlah kelas (mengajar masing-masing hanya pada subsampel yang sesuai). Dan pilih sebagai jawaban yang dikodekan oleh kelas dan otomatis yang memberikan perbedaan minimum antara gambar input dan gambar yang direkonstruksi. Itu tidak sulit untuk memeriksa MNIST: untuk melatih 10 auto-encoders (untuk setiap digit), menghitung akurasi, dan kemudian membandingkan dengan model multilayer yang sama dari classifier.

Skrip untuk pelatihan dan pengujian pada git (train_ae.py, calc_codes.py, calc_acc.py)

Arsitektur dan jumlah bobot:

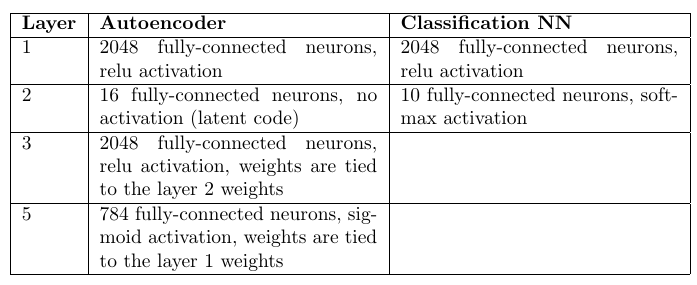
Pengkode Otomatis: 98,6%
Multilayer perceptron classifier: 98,4%

Pembaca yang penuh perhatian akan melihat bahwa ada 10 kali lebih banyak bobot dalam penyandi otomatis (berdasarkan jumlah mereka). Namun, peningkatan 10 kali lipat dalam jumlah bobot pada lapisan tersembunyi dalam perceptron multilayer hanya memperburuk statistik.

Tentu saja, jaringan konvolusi memberikan akurasi yang jauh lebih tinggi, tetapi tugasnya hanya membandingkan pendekatan, semua hal lain dianggap sama.

Akibatnya, dapat dicatat bahwa pendekatan dengan auto-encoders cukup kompetitif dengan jaringan yang terhubung penuh. Dan meskipun membutuhkan lebih banyak waktu untuk mengoptimalkan bobot, ia memiliki satu keuntungan penting: kemampuan untuk mendeteksi anomali dalam data input. Jika salah satu dari auto-encoders mampu merekonstruksi gambar input secara akurat, maka kita dapat menyatakan bahwa gambar anomali yang tidak terjadi dalam sampel pelatihan adalah input. Sebenarnya, Anda dapat merekonstruksi gambar bukan dari sampel input, tetapi apa yang harus dilakukan dalam situasi ini akan ditampilkan nanti.

Pertimbangkan satu pembuat enkode otomatis

Hal ini dimungkinkan dengan cara yang sedikit berbeda dari makalah di atas untuk melakukan analisis kualitatif hubungan antara kepadatan probabilitas dari data input p (x) dan respons dari autoencoder.

Auto Encoder - penggunaan berurutan dari fungsi encoder

z = g (x)

$z = g (x)$ dan decoder

x^{*} = f (z)

$x ^ * = f (z)$ dimana

x

$x$ Apakah vektor input, dan

z

$z$ - kinerja laten. Di beberapa bagian input (biasanya dekat dengan pelatihan)

x^{*} = x + n = f (g (x))

$x ^ * = x + n = f (g (x))$ dimana

n

$n$ - perbedaan. Kami menerima perbedaan dengan noise Gausovsky (parameternya dapat diperkirakan setelah melatih autencoder). Akibatnya, sejumlah asumsi yang cukup kuat dibuat:

1) perbedaan - Gaussian noise
2) auto encoder sudah "terlatih" dan berfungsi

Tapi, yang terpenting, hampir tidak ada batasan yang akan dikenakan pada auto-encoder itu sendiri.

Lebih lanjut, suatu estimasi kualitatif dari kerapatan probabilitas p (x) dapat diperoleh, atas dasar itu beberapa kesimpulan yang sangat penting di masa depan dapat dibuat.

Skor P (x) untuk satu enkoder otomatis

Kepadatan distribusi untuk

x d a l a m X

$x \ dalam X$ dan

z d a l a m Z

$z \ dalam Z$ terkait sebagai berikut:

p (x) = i n t_{z} p (x | z) p (z) d z (1)

$p (x) = \ int_ {z} p (x | z) p (z) dz \; \; \; (1)$

Kita perlu mendapatkan koneksi p (x) dan p (z). Untuk beberapa encoders otomatis, p (z) diatur pada tahap pelatihan mereka, untuk yang lain, p (z) masih lebih mudah diperoleh karena dimensi Z yang lebih kecil.

Distribusi kepadatan residu n diketahui, yang berarti:

p (n) = c o n s t k a l i e x p (- f r a c (x f (z))^{T} (x f (z)) 2 s i g m a^{2}) = p (x | z) (2)

$p (n) = const \ kali exp (- \ frac {(xf (z)) ^ T (xf (z))} {2 \ sigma ^ 2}) = p (x | z) \; \; ( 2)$

(x - f (z))^{T} (x - f (z))

$(x-f (z)) ^ T (x-f (z))$ Apakah jarak antara x dan proyeksi x *. Pada titik tertentu z * jarak ini akan mencapai batas minimum. Pada titik ini, sebagian turunan dari argumen eksponen dalam rumus (2) sehubungan dengan

z_{i}

$z_i$ (Sumbu Z) akan menjadi nol:

0 = f r a c p a r t i a l f (z^{*}) {p a r t i a l z_{i}}^{T} (x f (z^{*})) + (x f (z^{*}))^{T} f r a c p a r t i a l f (z^{*}) p a r t i a l z_{i}

$0 = \ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ frac {\ partial f (z ^ * )} {\ partial z_i}$

Di sini

f r a c p a r t i a l f (z^{*}) {p a r t i a l z_{i}}^{T} (x - f (z^{*}))

$\ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (x-f (z ^ *))$ skalar kemudian:

0 = f r a c p a r t i a l f (z^{*}) {p a r t i a l z_{i}}^{T} (x - f (z^{*})) (3)

$0 = \ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (x-f (z ^ *)) \; \; \; (3)$

Pilihan titik z *, di mana jaraknya

(x - f (z))^{T} (x - f (z))

$(x-f (z)) ^ T (x-f (z))$ minimal karena proses optimasi dari auto encoder. Selama pelatihan, residu kuadratik yang diminimalkan (sebagai aturan):

m i n l i m i t_{t h e t a, f o r a l l x d a l a m X t r a i n} L 2_{n o r m} (x - f_{} t h e t a (g_{} t h e t a (x)))

$\ min \ limit _ {\ theta, \ forall x \ dalam X train} L2_ {norm} ({x-f_ \ theta (g_ \ theta (x))})$ dimana

t h e t a

$\ theta$ - berat pembuat enkode. Yaitu setelah pelatihan g (x) cenderung z *.

Kami juga bisa berkembang

f (z)

$f (z)$ dalam seri Taylor (hingga istilah pertama) sekitar z *:

f (z) = f (z^{*}) + n a b l a f (z^{*}) (z - z^{*}) + o ((z - z^{*}))

$f (z) = f (z ^ *) + \ nabla f (z ^ *) (z-z ^ *) + o ((z-z ^ *))$

Jadi, sekarang persamaan (2) menjadi:

p (x | z) a p p r o x c o n s t k a l i e x p (- f r a c ((x f (z^{*})) - n a b l a f (z^{*}) (z z^{*}))^{T} ((x f (z^{*})) - n a b l a f (z^{*}) (z z^{*})) 2 s i g m a^{2}) =

$p (x | z) \ approx const \ kali exp (- \ frac {((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *)) ^ T ((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) =$

= c o n s t t i m e s e x p (- f r a c (x f (z^{*}))^{T} (x f (z^{*})) 2 s i g m a^{2}) e x p (- f r a c (n a b l a f (z^{*}) (z z^{*}))^{T} (n a b l a f (z^{*}) (z z^{*})) 2 s i g m a^{2}) k a l i

$= const \ times exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) exp (- \ frac {(\ nabla f (z ^ *) (zz ^ *)) ^ T (\ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) \ kali$

k a l i e x p (- f r a c (n a b l a f (z^{*}))^{T} (x f (z^{*})) + (x f (z^{*}))^{T} n a b l a f (z^{*})) (z z^{*}) 2 s i g m a^{2})

$\ kali exp (- \ frac {(\ nabla f (z ^ *)) ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ nabla f (z ^ *)) (zz ^ *)} {2 \ sigma ^ 2})$

Perhatikan bahwa faktor terakhir adalah 1 karena ekspresi (3). Faktor pertama dapat dihilangkan dengan tanda integral (tidak mengandung z) pada (1). Dan juga anggaplah bahwa p (z) adalah fungsi yang cukup halus dan tidak banyak berubah di lingkungan z *, yaitu ganti p (z) -> p (z *).

Setelah semua asumsi, integral (1) memiliki estimasi:

p (x) = c o n s t k a l i p (z^{*}) e x p (- f r a c (x f (z^{*}))^{T} (x f (z^{*})) 2 s i g m a^{2}) i n t_{z} e x p (- (z z^{*})^{T} W (x)^{T} W (x) (z z^{*})) d z, z^{*} = g (x)

$p (x) = const \ kali p (z ^ *) exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) \ int_ {z} exp (- (zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)) dz, \; \; \; z ^ * = g (x)$

dimana

W (x) = f r a c n a b l a f (z^{*}) s i g m a, z^{*} = g (x)

$W (x) = \ frac {\ nabla f (z ^ *)} {\ sigma}, z ^ * = g (x)$
Integral terakhir adalah integral Euler-Poisson n-dimensi:

i n t_{z} e x p (- f r a c (z z^{*})^{T} W (x)^{T} W (x) (z z^{*}) 2) d z = s q r t f r a c 1 d e t (W (x)^{T} W (x) / 2 p i)

$\ int_ {z} exp (- \ frac {(zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)} {2}) dz = \ sqrt {\ frac {1} {det ( W (x) ^ TW (x) / 2 \ pi)}}$

Hasilnya, kami mendapatkan taksiran akhir p (x):

p (x) = c o n s t k a l i e x p (- f r a c (x f (z^{*} *))^{T} (x f (z^{*})) 2 s i g m a^{2}) p (z^{*}) s q r t f r a c 1 d e t (W (x)^{T} W (x) / 2 p i), z^{*} = g (x) (4)

$p (x) = const \ kali exp (- \ frac {(xf (z ^ * *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) p (z ^ *) \ sqrt {\ frac {1} {det (W (x) ^ TW (x) / 2 \ pi)}}, z ^ * = g (x) \; \; \; (4)$

Semua matematika ini diperlukan untuk menunjukkan bahwa p (x) tergantung pada tiga faktor:

Jarak antara vektor input dan rekonstruksinya, semakin buruk dipulihkan, semakin kecil p (x)
Kerapatan probabilitas p (z *) pada z * = g (x)
Normalisasi fungsi p (z) pada titik z *, yang dihitung untuk autoencoder dari turunan parsial fungsi f

Dan dari konstanta normalisasi, yang selanjutnya akan bertanggung jawab untuk probabilitas a priori memilih auto encoder untuk menggambarkan data input.

Terlepas dari semua asumsi, hasilnya sangat berarti dan berguna dari sudut pandang perhitungan.

Klasifikasi parameter atau prosedur pemeringkatan

Sekarang Anda dapat lebih akurat menggambarkan prosedur klasifikasi menggunakan seperangkat auto-encoders:

Pelatihan pembuat enkode otomatis yang independen untuk setiap kelas pada output yang sesuai
Perhitungan matriks W untuk setiap autoencoder
Skor P (z) untuk setiap enkoder otomatis

Dan untuk setiap vektor input, Anda dapat mengevaluasi sekarang

p (x | k e l a s)

$p (x | kelas)$ dengan jumlah kelas. Dan ini akan menjadi fungsi kemungkinan yang diperlukan untuk pengambilan keputusan dalam kerangka aturan Bayesian untuk pengambilan keputusan.

Dengan cara yang sama, parameter yang tidak diketahui juga dapat diperkirakan dengan memecah ruang parameter menjadi nilai diskrit, dengan melatih pembuat enkode Anda sendiri untuk setiap nilai. Dan kemudian, berdasarkan skor Bayesian terbaik, pilih nilai yang memberikan fungsi kemungkinan maksimum.

Di sini perlu dicatat bahwa, secara formal, masalah memperkirakan p (z) tidak lebih sederhana daripada memperkirakan p (x). Tetapi dalam praktiknya tidak demikian. Ruang Z biasanya memiliki dimensi yang jauh lebih kecil, atau distribusi umumnya ditetapkan ketika mengoptimalkan bobot dari auto-encoder.

Gagasan menggabungkan ruang laten auto-encoders

Ada interpretasi aneh yang diajukan oleh Alexei Redozubov dan dijelaskan dalam artikel berikut:

Arsitektur Jaringan Saraf Tiruan Berbasis Transformasi Konteks dalam Kolom Kortikal. Vasily Morzhakov, Alexey Redozubov
Holographic Memory: Sebuah model baru dari pemrosesan informasi oleh Neural Microcircuits. Alexey Redozubov, Springer
Bukan jaringan saraf sama sekali. Morzhakov V.

Informasi dapat memiliki interpretasi yang sangat berbeda dalam konteks yang berbeda. Model "seperangkat pembuat enkode otomatis" menggemakan gagasan yang diajukan ini. Penyandi otomatis apa pun adalah model laten dari data input dalam konteks yang sama (satu kelas atau parameter tetap lainnya), mis. vektor laten adalah interpretasi, dan setiap auto-encoder adalah sebuah konteks. Setelah menerima informasi input, itu dipertimbangkan dalam setiap konteks (oleh masing-masing auto-encoder), dan konteks dipilih yang kemungkinan besar mempertimbangkan model yang ada di setiap auto-encoder.

Langkah masuk akal berikutnya adalah untuk memungkinkan persimpangan interpretasi dalam konteks yang berbeda. Yaitu selama pelatihan, kita sering tahu bahwa interpretasinya tetap sama, tetapi bentuk presentasi (konteks) berubah. Misalnya, orientasi suatu objek berubah, tetapi objeknya tetap sama. Vektor deskripsi objek harus dilestarikan, dan konteks - orientasi berubah.

Kemudian, jika kita melihat pada rumus (4), maka faktor p (z) ternyata diperkirakan untuk seluruh rangkaian auto-encoders, dan tidak untuk masing-masing secara terpisah. Interpretasi (vektor laten) akan memiliki distribusi yang sama. Untuk sejumlah kecil auto-encoders, ini mungkin tidak memiliki peran yang signifikan, tetapi dalam tugas nyata jumlah ini bisa sangat besar. Misalnya, jika Anda menetapkan satu konteks untuk setiap kemungkinan orientasi objek 3D, mungkin ada ratusan ribu di antaranya. Sekarang, setiap contoh yang disajikan untuk pelatihan dalam konteks apa pun akan membentuk distribusi p (z).

Pertukaran interpretasi dan konteks

Dalam masalah yang diterapkan, pertanyaan segera muncul: apa yang ditugaskan oleh interpretasi, dan apa menurut konteks? Konteks dan interpretasi dapat dengan mudah dipertukarkan, dan tidak ada yang mengecualikan kemungkinan fungsi paralel simultan dari sepasang "set autoencoder".

Untuk kejelasan, Anda dapat menawarkan contoh ini:

Gambar input berisi wajah orang.

konteks - orientasi wajah. Kemudian, untuk rekonstruksi gambar input, kami tidak memiliki cukup "interpretasi" - kode yang mengidentifikasi seseorang, yang akan berisi deskripsi wajah, gaya rambut, pencahayaannya. Selama pelatihan, kita perlu menampilkan wajah yang sama dari sisi yang berbeda, "membekukan" kode laten, sambil mengubah orientasi.
konteks - jenis wajah, pencahayaan, gaya rambut. Kemudian, untuk rekonstruksi gambar input, kita tidak memiliki orientasi wajah. Selama pelatihan, akan perlu untuk menunjukkan wajah yang berbeda dalam kondisi pencahayaan yang berbeda, tetapi dengan orientasi yang sama.

Keputusan Bayesian optimal dalam kasus pertama akan dibuat mengenai orientasi wajah, dan yang kedua - tipenya. Agaknya, opsi pertama akan memberikan akurasi orientasi yang lebih baik, dan yang kedua akan lebih akurat mengevaluasi wajah siapa itu.

Mempelajari seperangkat penyandian otomatis dengan ruang laten bersama

Dalam pelatihan, kita perlu tahu bagaimana satu entitas dalam hal makna terlihat dalam konteks yang berbeda. Sebagai contoh, jika kita berbicara tentang gambar angka dan orientasi konteks, maka secara garis besar pelatihan silang tersebut terlihat seperti ini:

Encoder dari satu auto-encoder digunakan, maka kode laten didekodekan oleh decoder auto-encoder lainnya. Fungsi kehilangan pembelajaran tetap standar. Sangat menarik bahwa jika auto-encoder dipilih simetris (mis., Bobot encoder dan decoder terhubung), maka dalam setiap iterasi semua bobot dari kedua auto-encoders dioptimalkan.

Yang paling nyaman untuk pelatihan yang rumit seperti itu adalah PyTorch, yang memungkinkan Anda membuat skema yang cukup rumit untuk memperbanyak kesalahan, termasuk yang dinamis.

Langkah-langkah pembelajaran standar setiap encoder otomatis bergantian dengan iterasi pelatihan silang. Akibatnya, semua auto-encoders memiliki ruang laten umum atau "interpretasi" dalam konteks yang berbeda.

Sangat penting bahwa sebagai hasil dari analisis seperti itu kita akan dapat membagi informasi yang dimasukkan ke dalam "konteks" dan "interpretasi".

Contoh pelatihan

Pertimbangkan contoh yang cukup sederhana berdasarkan MNIST, yang akan membantu menunjukkan prinsip pelatihan autoencoder dengan ruang laten yang umum. Sebagai hasilnya, contoh ini akan menunjukkan pembentukan konsep abstrak "kubus" menggunakan mekanisme yang dijelaskan dalam artikel.

Angka-angka dari MNIST diplot di tepi kubus dan berputar di sekitar salah satu sumbunya:

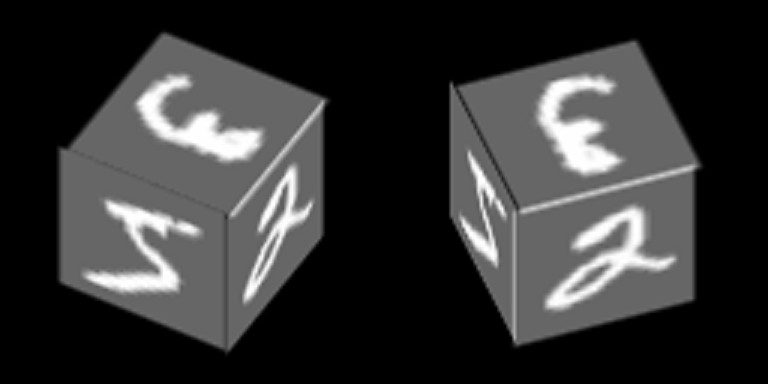
Kami akan melatih autoencoder untuk mengembalikan wajah, konteks - orientasi wajah.

Berikut adalah contoh angka "nol" dalam 100 konteks, 34 yang pertama sesuai dengan sudut rotasi yang berbeda dari sisi samping, dan 76 sisanya - sudut rotasi yang berbeda dari sisi atas.

Kami berasumsi bahwa untuk masing-masing dari 100 gambar ini "interpretasi" harus sama, dan kombinasi acak mereka yang digunakan untuk pelatihan silang.

Setelah pelatihan dengan metode yang dijelaskan di atas, adalah mungkin untuk mencapai bahwa kode laten dari salah satu autoencoder dapat didekodekan oleh autoencoder lain, memperoleh konversi kontekstual yang sangat bermakna.

Misalnya, gambar ini menunjukkan bagaimana hasil enkode dari auto encoder di nomor 10 diterjemahkan oleh auto encoders lain untuk salah satu digit:

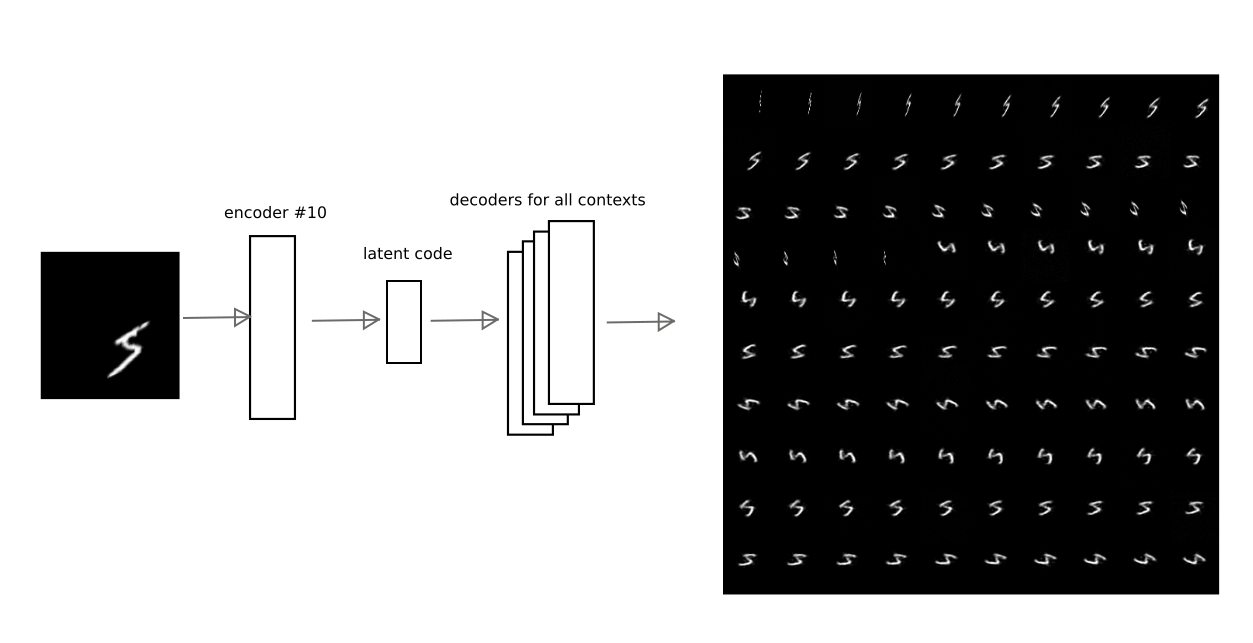
Dengan demikian, memiliki kode "interpretasi", yaitu vektor laten dari pembuat enkode otomatis, Anda dapat mengembalikan gambar asli di salah satu konteks terlatih (mis., dekoder dari pembuat enkode otomatis apa pun).

Input masking vektor

Dalam rumus (4), dispersi residu

s i g m a

$\ sigma$ , yang dipilih oleh konstanta untuk salah satu komponen vektor input. Namun, jika beberapa komponen tidak memiliki hubungan statistik dengan model laten, maka varians mungkin akan secara signifikan lebih tinggi untuk komponen ini. Dispersi ada di mana-mana dalam penyebut, yang berarti bahwa semakin besar perbedaan, semakin sedikit kontribusi kesalahan komponen. Anda dapat menghubungkan ini sebagai masking dari beberapa bagian dari vektor input.

Untuk contoh ini dengan wajah berputar, topeng terlihat jelas - proyeksi wajah dalam konteks tertentu.

Dalam pendekatan yang disederhanakan dalam contoh ini, yang hanya menggunakan residu antara gambar input dan rekonstruksi, Anda hanya perlu mengalikan residu dengan mask untuk masing-masing konteks.

Dalam kasus umum, perlu untuk lebih ketat mengevaluasi parameter distribusi, sehingga tanpa memasukkan topeng secara manual.

Pemisahan interpretasi dari konteks

Memisahkan interpretasi dari konteks, Anda bisa mendapatkan konsep abstrak. Dalam contoh yang dilatih, menarik untuk menunjukkan 2 efek:

1) belajar sekali pakai, mis. pelatihan dengan jumlah contoh yang sangat kecil (dalam batas satu).

Jika kita hanya menganalisis interpretasi, mengabaikan konteks, maka menjadi mungkin untuk mengenali gambar baru dalam orientasi wajah yang berbeda, ketika gambar baru ditampilkan hanya dalam salah satu orientasi.

Penting untuk dicatat bahwa gambar baru harus disajikan. Demi kebenaran, kami juga menetapkan tujuan mengingat bukan hanya satu gambar, tetapi juga mempelajari cara berbagi 2 gambar baru yang sebelumnya tidak ditemukan di pusat pelatihan MNIST. Misalnya, seperti:

Idenya adalah sebagai berikut: perlihatkan tanda-tanda ini di salah satu konteks geometris (misalnya, di bawah nomor 10), pilih hyperplane yang berjalan sama dari interpretasi tanda-tanda ini, dan kemudian pastikan bahwa dengan hyperplane ini kita bisa mengenali tanda apa yang disajikan kepada kita ketika wajah diputar (konteks lain).

Penting untuk dicatat di sini bahwa pembuat enkode otomatis tidak akan dilatih tentang tanda-tanda baru. Karena variasi angka yang ada di MNIST, Anda dapat memprediksi bagaimana karakter baru yang belum pernah terlihat sebelumnya akan terlihat dalam konteks yang berbeda.

Jadi tanda V akan terlihat setelah pengkodean dalam konteks No. 10 dan penguraian dalam yang tersisa:

Dapat dilihat bahwa prediksi tersebut tidak sempurna, tetapi dapat dikenali secara visual.

Kami menyatakan demonstrasi ini sebagai "percobaan 1" dan menggambarkan hasilnya di bawah ini.

2) dan dengan kubus itu menarik untuk menunjukkan apa yang akan terjadi jika Anda mengabaikan konten vektor laten, dan hanya tingkat masuk akal dari setiap encoder otomatis disampaikan.

Mari kita lihat seperti apa kemungkinannya untuk masing-masing konteks untuk dua kubus dengan tekstur yang sangat berbeda (angka 5 dan 9) untuk 100 konteks yang dapat ditampilkan sebagai peta:

Dapat dilihat bahwa peta-peta itu sangat mirip, meskipun teksturnya berbeda di sisi kubus.

Yaituvektor itu sendiri, yang berisi kemungkinan model autoencoder (konteks), memungkinkan kita untuk merumuskan konsep abstrak baru yang terkait dengan bentuk kubus 3 dimensi. Vektor ini juga dapat dideskripsikan pada level selanjutnya oleh auto-encoder yang mempelajari model kubus.

Dalam percobaan kedua, akan diperlukan untuk membuat tingkat kedua pemrosesan informasi untuk melatih auto-encoder dari model kubus abstrak. Dan kemudian, menggunakan proyeksi belakang untuk mengembalikan gambar asli untuk implementasi berbeda dari model kubus ini. Sederhananya, buat kubus berputar.

Hasil dari "percobaan nomor 1"

Set auto-encoders yang dilatih oleh MNIST berlaku untuk dua gambar baru yang disajikan dalam konteks # 10. Ternyata 2 poin dalam ruang laten yang sesuai dengan tanda-tanda V dan +. Kami mendefinisikan bidang yang berjarak sama dari kedua titik, yang akan kami gunakan untuk mengambil keputusan. Jika titik berada di satu sisi pesawat - tanda V, di sisi lain - tanda plus.

Sekarang kita mendapatkan kode dari gambar yang dikonversi dan untuk masing-masing kita menghitung jarak ke pesawat, melestarikan tanda.

Sebagai hasilnya, adalah mungkin untuk membedakan tanda apa yang disajikan untuk 100 konteks.

Distribusi jarak pada grafik:

Visualisasi hasil menggunakan simbol individu sebagai contoh:

Yaitukode laten tanda V dalam konteks yang benar-benar berbeda jauh lebih dekat satu sama lain dalam ruang laten daripada kode tanda V dan tambah dalam konteks yang sama. Karena itu, dalam 100 dari 100 kasus, dimungkinkan untuk berhasil membedakan tanda-tanda dalam berbagai orientasi wajah kubus, meskipun pada kenyataannya hanya satu sampel dari masing-masing tanda disajikan.

Itu mungkin untuk menunjukkan "pembelajaran sekali pakai" klasik, yang tidak mungkin dilakukan dalam arsitektur asli jaringan saraf tiruan. Prinsip dasar yang digunakan pendekatan ini sangat mirip dengan "transfer pembelajaran" yang ditunjukkan, misalnya, dalam artikel ini .

Tautan ke git (train_ae_shared.py, test_AB.py)

Hasil dari "percobaan nomor 2"

Memisahkan interpretasi dari konteks juga memungkinkan pembelajaran dari sekumpulan contoh terbatas. Adalah mungkin untuk menunjukkan hanya satu dari interpretasi yang mungkin dalam berbagai konteks (memperbaiki "vektor laten"). Model kubus abstrak dapat diperoleh hanya dengan menunjukkan hanya satu digit di semua wajah.

Percobaan ini disusun sebagai berikut:

Basis pelatihan sedang dipersiapkan: kubus dengan derajat rotasi dari 0 hingga 90 derajat. Di wajah kubus adalah nomor 5.
Vektor kemungkinan konteks, terpisah dari interpretasi (kode laten), diteruskan ke tingkat berikutnya, di mana auto-encoder yang bertanggung jawab untuk model kubus dilatih
: , «», , , , , .

Sampel pelatihan terdiri dari 5421 gambar dengan gambar angka 5 di sisinya, contoh:

kubus dengan rotasi dari 0 hingga 90 derajat.

Kita tahu sebelumnya bahwa kubus hanya memiliki satu derajat kebebasan rotasi, oleh karena itu auto-encoder di tingkat kedua hanya memiliki satu komponen dalam kode laten. Setelah pelatihan, Anda dapat memvariasikan komponen ini dari 0 hingga 1 (fungsi sigmoid dipilih untuk mengaktifkan lapisan laten) dan melihat mana vektor kemungkinan konteks direproduksi selama decoding:

Kemudian vektor ini ditransfer ke level 1, di mana 100 konteks orientasi wajah, maxima lokal dan membayangkan "kode laten dari tanda di wajah kubus. "Bayangkan" angka 3 pada wajah, mengubah vektor laten di auto-encoder yang bertanggung jawab atas konsep abstrak kubus, dan dapatkan gambar kubus berikut:

Atau kode tanda V, yang tidak ditemukan sama sekali dalam rangkaian pelatihan:

Kualitasnya lebih buruk, tetapi tanda itu dapat dikenali.

Dengan demikian, pada level kedua dari pemrosesan gambar, kami mendapatkan auto encoder yang memodelkan berbagai konsep abstrak "cube". Dalam prakteknya, dalam masalah pengenalan, prinsip proyeksi belakang yang ditunjukkan dalam percobaan sangat penting, karena memungkinkan untuk menghilangkan ambiguitas interpretasi karena pembentukan konsep-konsep abstrak dari tingkat yang lebih tinggi.

Tautan ke git (second_level.py, second_level_test.py)

Contoh lain di mana pemisahan konteks bekerja

Dalam artikel saya sebelumnya, ketika mengenali nomor mobil, metode yang sama digunakan tanpa penjelasan. Posisi, orientasi, dan skala angka-angka dalam gambar dipisahkan dari isinya, tingkat selanjutnya mempersepsikan data ini untuk membangun model "nomor mobil". Tidak peduli nomor berapa pun, konfigurasi geometrik timbal baliknya adalah penting, sehingga kami dapat dengan yakin mengatakan bahwa ini adalah nomor mobil (omong-omong, juga konsep abstrak).

Dengan analogi, kita dapat memberikan sejumlah contoh lain dari visi komputer: bentuk 3D suatu objek atau konturnya dapat dipisahkan dari tekstur dan latar belakangnya; enumerasi komponen dalam isolasi dari konfigurasi spasial timbal balik juga sering memungkinkan pembentukan konsep abstrak baru.

, : — ( ) ( ); ( , ,«- -»).

Saat ini, sulit untuk merumuskan bagaimana AI yang kuat berbeda dari yang lemah. Mungkin, daftar ini harus mencakup semua yang kurang dalam pendekatan dan algoritma yang ada agar komputer dapat bertindak seefisien seseorang, misalnya:

Membuat keputusan, menggunakan strategi, menyelesaikan dalam menghadapi ketidakpastian. Ketidakpastian yang tinggi mengharuskan pemilihan model terbaik yang diformulasikan selama pelatihan
Refleksi model dunia fisik dan sosial sekitarnya, termasuk kesadaran diri dan kesadaran orang lain
Mekanisme pemikiran abstrak, memungkinkan untuk merumuskan konsep yang dapat digunakan pada berbagai input data selanjutnya
Kemampuan untuk "menguraikan" pikiran Anda sendiri

Juga, jelas tidak ada cukup mekanisme memori yang dikembangkan yang diintegrasikan dengan proses pembelajaran, mekanisme promosi / hukuman.

Artikel menunjukkan pendekatan untuk masalah pengakuan dan estimasi parameter, yang didasarkan pada pemilihan model terbaik yang menggambarkan input data. Diasumsikan bahwa ini adalah mekanisme untuk memilih interpretasi dan konteks terbaik. Karena pemisahan interpretasi dan konteks pada output modul (satu set auto-encoders), seseorang dapat merumuskan konsep abstrak atau menggeneralisasi pengalaman dalam isolasi dari konteks, sehingga mengurangi sampel pelatihan. Set konteks dapat mencerminkan pembacaan sensor mesin (orientasi, posisi, kecepatan, dll.), Yang memungkinkan pembelajaran alami tanpa guru menjadi mungkin.

Selain itu, meskipun Deep learning digunakan dalam pelatihan autoencoder, proses yang terjadi pada autoencoder mudah dianalisis pada setiap tingkat pemrosesan informasi, karena adalah mungkin untuk menentukan dalam model mana (atau dalam konteks apa) interpretasi terbaik ditemukan. Dan arti dari umpan balik antara tingkat yang perlu diperkenalkan dalam sistem yang kompleks adalah untuk meningkatkan atau mengurangi kemungkinan memilih konteks tertentu.

Hasil

Suatu perangkat matematika diusulkan, atas dasar mana seseorang dapat memilih satu atau model lain yang menggambarkan data input, dipandu oleh aturan keputusan Bayesian. Model diperoleh menggunakan autoencoder dengan ruang laten yang umum. Suatu ide diusulkan sesuai dengan mana kode laten dari auto-encoder adalah interpretasi, dan model laten, yaitu encoder otomatis itu sendiri adalah konteks.

Hal ini menunjukkan bahwa set auto-encoders tidak kalah dalam akurasi untuk jaringan saraf tiruan yang sepenuhnya terhubung menggunakan contoh MNIST.

Efek memisahkan interpretasi dari konteks ditunjukkan: minimalisasi set data yang diperlukan (dalam batas "pembelajaran sekali pakai") untuk pengenalan gambar yang baru disajikan karena pra-pelatihan data lainnya.

Efek memisahkan konteks dari interpretasi ditunjukkan: kemungkinan membentuk konsep abstrak tingkat berikutnya menggunakan "kubus" abstraksi geometris sebagai contoh.

Referensi

1) Alain, G. dan Bengio, Y. Apa yang dipelajari autoencoder teratur dari distribusi data menghasilkan. 2013
2) Kamyshanska, H. 2013. Pada penilaian autoencoder
3) Daniel Jiwoong Im, Mohamed Ismael Belghazi, Roland Memisevic. 2016. Kekayaan dari Auto-Encoders Terikat
4) Arsitektur Jaringan Syaraf Tiruan Berdasarkan Transformasi Konteks dalam Kolom Kortikal. Vasily Morzhakov, Alexey Redozubov
5) Memori Holografik: Model novel pemrosesan informasi oleh Neural Microcircuits. Alexey Redozubov, Springer
6) Bukan jaringan saraf sama sekali. Morzhakov V.
7) en.wikipedia.org/wiki/Gaussian_integral
8) Contoh permusuhan: Serangan dan Pertahanan untuk Pembelajaran Jauh
9) Pembelajaran Imitasi Satu Pemotretan

PS: Artikel ini adalah pracetak elektronik berbahasa Rusia, diterbitkan untuk membahas hasil, mencari kesalahan. Setiap kritik konstruktif dipersilahkan!

Pengkode Otomatis dan Kecerdasan Buatan yang Kuat