
Properti bilangan prima jarang memungkinkan Anda untuk bekerja dengannya secara berbeda daripada dalam bentuk array yang sudah dihitung sebelumnya - dan lebih disukai sebanyak mungkin. Format penyimpanan alami dalam bentuk bilangan bulat dari satu atau beberapa kapasitas digit lainnya menderita pada saat yang sama dari beberapa kerugian yang menjadi signifikan dengan pertumbuhan volume data.
Jadi, format bilangan bulat tak bertanda 16-bit dengan ukuran tabel semacam itu sekitar 13 kilobyte, hanya berisi 6542 bilangan prima: diikuti oleh angka 65531 adalah nilai-nilai kedalaman bit yang lebih tinggi. Meja seperti itu hanya cocok sebagai mainan.
Format integer 32-bit paling populer dalam pemrograman terlihat jauh lebih solid - ini memungkinkan Anda untuk menyimpan sekitar 203 juta yang sederhana. Tetapi meja seperti itu sudah menempati sekitar 775 megabita.
Format 64-bit memiliki lebih banyak prospek. Namun, dengan kekuatan teoretis dari urutan nilai 1e + 19, tabel akan memiliki ukuran 64 exabytes.
Tidak benar-benar percaya bahwa kemanusiaan progresif kita akan pernah di masa mendatang menghitung tabel bilangan prima dari volume seperti itu. Dan intinya di sini tidak begitu banyak dalam volume bahkan seperti pada waktu penghitungan algoritma yang tersedia. Katakanlah, jika tabel semua 32-bit yang sederhana masih dapat dihitung secara mandiri dalam beberapa jam (Gbr. 1), maka untuk tabel setidaknya urutan besarnya lebih besar akan memakan waktu beberapa hari. Tetapi volume seperti hari ini - ini hanya level awal.
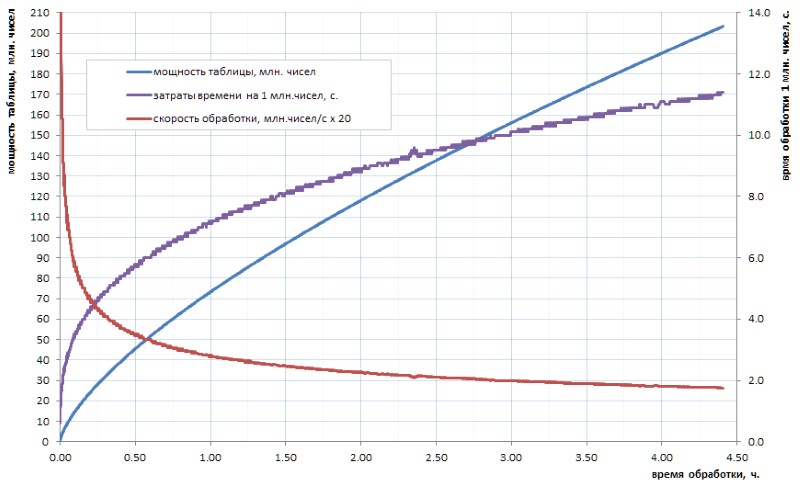
Seperti dapat dilihat dari diagram, waktu perhitungan spesifik setelah brengsek mulai dengan lancar beralih ke pertumbuhan asimptotik. Dia agak lambat. tetapi ini adalah pertumbuhan, yang berarti menambang setiap bagian data selanjutnya dari waktu ke waktu akan semakin sulit. Jika Anda ingin membuat beberapa terobosan signifikan, Anda harus memparalelkan pekerjaan di seluruh core (dan itu paralel dengan baik) dan menggantungnya di superkomputer. Dengan prospek mendapatkan 10 miliar pertama sederhana dalam seminggu, dan 100 miliar - hanya dalam setahun. Tentu saja, ada algoritma yang lebih cepat untuk menghitung sederhana daripada bust sepele yang digunakan dalam pekerjaan rumah saya, tetapi, pada dasarnya, ini tidak mengubah masalah: setelah dua atau tiga urutan besarnya, situasinya menjadi serupa.
Oleh karena itu, alangkah baiknya jika pernah melakukan pekerjaan penghitungan, untuk menyimpan hasilnya dalam bentuk tabel siap pakai, dan menggunakannya sesuai kebutuhan.
Karena ide yang jelas, jaringan menemukan banyak tautan ke daftar bilangan prima yang sudah jadi yang sudah dihitung oleh seseorang. Sayangnya, dalam kebanyakan kasus mereka hanya cocok untuk kerajinan siswa: satu seperti itu, misalnya, mengembara dari situs ke situs dan mencakup 50 juta yang sederhana. Jumlah ini hanya dapat memukau yang belum tahu: sudah disebutkan di atas bahwa pada komputer rumah dalam beberapa jam Anda dapat menghitung sendiri tabel semua 32-bit yang sederhana, dan empat kali lebih besar. Mungkin sekitar 15-20 tahun yang lalu, daftar seperti itu memang merupakan pencapaian heroik bagi komunitas awam. Saat ini, di era multi-core multi-gigahertz dan perangkat multi-gigabyte, ini tidak lagi mengesankan.
Saya beruntung bisa berkenalan dengan akses ke meja sederhana yang lebih representatif, yang akan saya gunakan lebih jauh sebagai ilustrasi dan pengorbanan untuk eksperimen lapangan saya. Untuk tujuan konspirasi, saya akan memanggilnya 1TPrimo . Ini berisi semua bilangan prima kurang dari satu triliun.
Menggunakan 1TPrimo sebagai contoh, mudah untuk melihat volume apa yang harus Anda tangani. Dengan kapasitas sekitar 37,6 miliar nilai dalam format integer 64-bit, daftar ini adalah 280 gigabytes. By the way - bagian itu yang bisa muat dalam 32 digit hanya menyumbang 0,5% dari jumlah angka yang diwakili di dalamnya. Ini membuatnya sangat jelas bahwa setiap pekerjaan serius dengan bilangan prima pasti cenderung total kedalaman 64-bit (atau lebih).
Dengan demikian, kecenderungan suramnya jelas: entah bagaimana tabel bilangan prima yang serius pasti memiliki volume yang sangat besar. Dan kita entah bagaimana harus melawan ini.
Hal pertama yang terlintas dalam pikiran ketika melihat sebuah tabel (Gbr. 2) adalah bahwa ia terdiri dari nilai-nilai berurutan yang hampir identik yang hanya berbeda dalam satu atau dua tempat desimal terakhir:
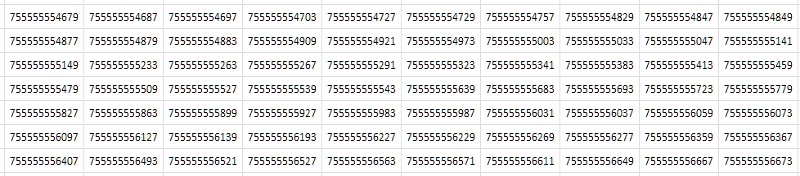
Secara sederhana, dari pertimbangan abstrak yang paling umum: jika file memiliki banyak data duplikat, maka file tersebut harus dikompres dengan baik oleh pengarsipan. Memang, kompresi tabel 1TPrimo dengan utilitas 7-zip yang populer pada pengaturan standar memberikan rasio kompresi yang agak tinggi: 8,5. Benar, waktu pemrosesan - dengan ukuran besar tabel sumber - pada server 8-inti, dengan beban rata-rata semua inti sekitar 80-90%, adalah 14 jam 12 menit. Algoritma kompresi universal dirancang untuk beberapa ide abstrak dan umum tentang data. Dalam beberapa kasus khusus, algoritma kompresi khusus yang dibangun di atas fitur-fitur terkenal dari kumpulan data yang masuk dapat menunjukkan indikator yang jauh lebih efektif, yang dikhususkan untuk pekerjaan ini. Dan seberapa efektif itu akan menjadi jelas di bawah ini.
Nilai numerik dekat dari bilangan prima tetangga meminta keputusan untuk tidak menyimpan nilai-nilai ini sendiri, tetapi interval (perbedaan) di antara mereka. Dalam hal ini, penghematan yang signifikan dapat dicapai karena fakta bahwa kedalaman bit dari interval jauh lebih rendah daripada kedalaman bit dari data awal (Gbr. 3).
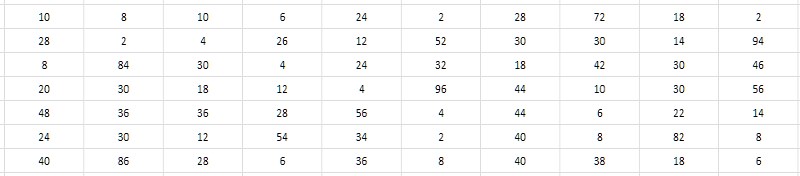
Dan tampaknya itu tidak tergantung pada kedalaman bit dari yang sederhana menghasilkan interval. Pencarian lengkap menunjukkan bahwa nilai-nilai khas interval untuk bilangan prima yang diambil dari berbagai tempat dalam tabel 1TPrimo berada dalam satuan, puluhan, kadang-kadang ratusan, dan - sebagai kalimat kerja pertama - mereka mungkin bisa masuk ke dalam kisaran 8-bit bilangan bulat yang tidak ditandatangani, mis., byte. Akan sangat nyaman, dan dibandingkan dengan format 64-bit, ini akan segera mengarah pada kompresi data 8 kali lipat - hanya di suatu tempat di tingkat yang ditunjukkan oleh pengarsipan 7-zip. Selain itu, kesederhanaan algoritma kompresi dan dekompresi pada prinsipnya memiliki dampak besar pada kecepatan kompresi dan akses ke data dibandingkan dengan 7-zip. Kedengarannya menggoda.
Sangat jelas bahwa data yang dikonversi dari nilai absolut ke interval relatif di antara mereka hanya cocok untuk memulihkan serangkaian nilai yang muncul secara berurutan dari awal tabel utama. Tetapi jika kita menambahkan struktur indeks blok minimal ke tabel interval seperti itu, maka dengan biaya overhead tambahan yang tidak signifikan ini akan memungkinkan kita untuk mengembalikan - tetapi sudah blok demi blok - baik elemen tabel dengan nomornya maupun elemen terdekat dengan nilai yang ditetapkan secara sewenang-wenang, dan operasi ini, bersama dengan operasi utama sampel urutan - secara umum, itu menguras bagian terbesar dari pertanyaan yang mungkin untuk data tersebut. Pemrosesan statistik, tentu saja, akan menjadi lebih rumit, tetapi masih akan tetap cukup transparan tidak ada trik khusus dalam memulihkannya "on the fly" dari interval yang tersedia saat mengakses blok data yang diperlukan.
Tapi sayang sekali. Eksperimen numerik sederhana pada data 1TPrimo menunjukkan bahwa sudah pada akhir dari puluhan juta ketiga (ini kurang dari seperseratus persen dari volume 1TPrimo) - dan kemudian di tempat lain - interval antara bilangan prima yang berdekatan secara teratur berada di luar kisaran 0,255.
Namun demikian, percobaan numerik yang sedikit rumit mengungkapkan bahwa pertumbuhan interval maksimum antara bilangan prima tetangga dengan pertumbuhan tabel itu sendiri sangat, sangat lambat - yang berarti idenya masih bagus dalam beberapa hal.
Yang kedua, melihat lebih dekat pada tabel interval menunjukkan bahwa mungkin untuk menyimpan bukan perbedaan itu sendiri, tetapi setengahnya. Karena semua bilangan prima lebih besar dari 2 jelas aneh, masing-masing, perbedaan mereka jelas genap. Dengan demikian, perbedaan dapat dikurangi 2 tanpa kehilangan nilai; dan untuk kelengkapan, kita juga dapat mengurangi satu dari hasil bagi yang diperoleh untuk menggunakan nilai nol yang tidak diklaim sebaliknya (Gbr. 4). Pengurangan interval seperti itu akan disebut selanjutnya monolitik, berbeda dengan bentuk awal yang longgar dan keropos, di mana semua nilai ganjil dan nol ternyata tidak diklaim.
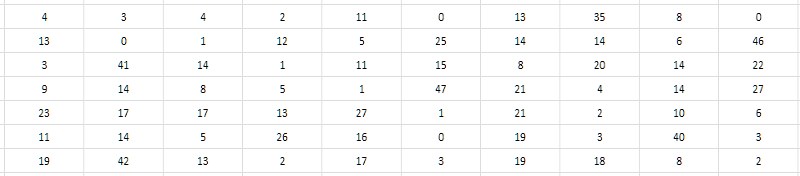
Perlu dicatat bahwa karena interval antara dua yang pertama sederhana (2 dan 3) tidak cocok dengan skema ini, maka 2 harus dikeluarkan dari tabel interval dan ingat fakta ini setiap saat.
Teknik sederhana ini memungkinkan Anda untuk menyandikan interval dari 2 hingga 512 pada rentang nilai 0..255. Sekali lagi, harapan menjadi hidup bahwa metode perbedaan akan memungkinkan kita untuk mengemas urutan bilangan prima yang jauh lebih kuat. Dan memang demikian: serangkaian nilai 37,6 miliar yang disajikan dalam daftar 1TPrimo hanya mengungkapkan 6 (enam!) Interval yang tidak berada dalam kisaran 2..512.
Tapi itu kabar baik; yang buruk adalah bahwa keenam interval ini tersebar di daftar dengan cukup bebas, dan yang pertama terjadi pada akhir sepertiga pertama daftar, mengubah dua pertiga sisanya menjadi pemberat yang tidak cocok untuk metode kompresi ini (Gbr. 5):
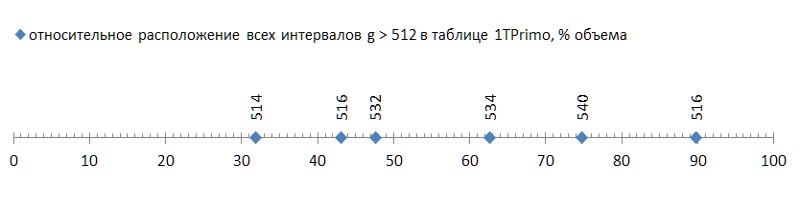
Seperti flush (enam potong malang selama hampir empat puluh miliar! - dan pada Anda ...) bahkan dengan lalat di salep untuk membandingkan - untuk menunjukkan kehormatan tar. Namun sayang, ini sebuah pola, bukan kecelakaan. Jika kita melacak tampilan pertama interval antara bilangan prima tergantung pada panjang data, menjadi jelas bahwa fenomena ini terletak pada genetika bilangan prima, meskipun itu berkembang sangat lambat (Gambar 6 *).
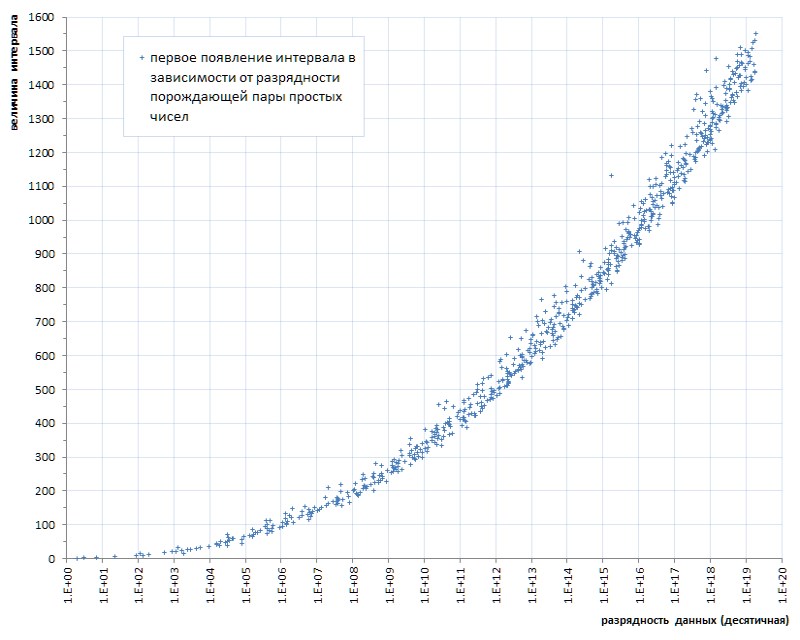
* Jadwal disusun sesuai dengan situs tematik Thomas R. Nisley ,
yang beberapa perintah besarnya lebih unggul dari kekuatan daftar 1TPrimo
Tetapi bahkan kemajuan yang sangat lambat ini secara jelas mengisyaratkan: seseorang dapat membatasi diri pada kedalaman bit tertentu dari suatu interval hanya pada kekuatan tertentu dari daftar yang telah ditentukan. Artinya, itu tidak cocok sebagai solusi universal.
Namun, fakta bahwa metode yang diusulkan untuk mengompresi urutan bilangan prima memungkinkan Anda untuk mengimplementasikan tabel kompak sederhana dengan kapasitas hampir 12 miliar nilai sudah cukup hasilnya. Tabel seperti ini menempati volume 11,1 gigabytes - melawan 89,4 gigabytes dalam format 64-bit yang sepele. Tentunya untuk sejumlah aplikasi solusi semacam itu mungkin sudah cukup.
Dan yang menarik: prosedur untuk menerjemahkan tabel 1TPrimo 64-bit ke format interval 8-bit dengan struktur blok, hanya menggunakan satu inti prosesor (untuk paralelisasi, Anda harus menggunakan komplikasi program yang signifikan, dan itu benar-benar tidak sepadan) dan tidak lebih dari 5 % dari beban prosesor (sebagian besar waktu dihabiskan untuk operasi file) hanya membutuhkan 19 menit Terhadap - Saya ingat - 14 jam pada delapan core pada 80-90% dari beban yang dihabiskan oleh pengarsipan 7-zip.
Tentu saja, hanya sepertiga pertama dari tabel yang dikenakan terjemahan ini, di mana rentang interval tidak melebihi 512. Oleh karena itu, jika kita membawa 14 jam penuh ke sepertiga yang sama, maka 19 menit harus dibandingkan dengan hampir 5 jam dari pengarsipan 7-zip. Dengan jumlah kompresi yang sebanding (8 dan 8,5), perbedaannya sekitar 15 kali. Mempertimbangkan bahwa bagian terbesar dari waktu kerja program siaran ditempati oleh operasi file, perbedaannya bahkan akan lebih curam pada sistem disk yang lebih cepat. Dan secara intelektual, waktu operasi 7-zip pada delapan core masih harus dihitung pada satu utas, dan kemudian perbandingannya akan menjadi sangat memadai.
Pemilihan dari basis data semacam itu sangat sedikit berbeda dalam waktu dari pemilihan dari tabel data yang dibongkar dan hampir seluruhnya ditentukan oleh waktu operasi file. Angka-angka spesifik sangat tergantung pada perangkat keras tertentu, pada server saya, rata-rata, akses ke blok data sewenang-wenang mengambil 37,8 μs, sementara membaca blok berurutan - 4,2 μs per blok, untuk membongkar lengkap blok - kurang dari 1 μs. Artinya, tidak masuk akal untuk membandingkan dekompresi data dengan karya pengarsip standar. Dan ini merupakan nilai tambah yang besar.
Dan, akhirnya, pengamatan menawarkan lagi, solusi ketiga yang menghilangkan batasan pada kekuatan data: interval coding dengan nilai-nilai panjang variabel. Teknik ini telah lama digunakan dalam aplikasi terkait kompresi. Artinya adalah jika ditemukan dalam input bahwa beberapa nilai sering ditemukan, beberapa kurang umum, dan beberapa sangat jarang, maka kita dapat menyandikan yang pertama dengan kode pendek, yang kedua dengan kode yang lebih otentik, dan yang ketiga - sangat panjang (mungkin bahkan sangat lama, karena itu tidak masalah: semua sama, data seperti itu sangat jarang). Akibatnya, total panjang kode yang diterima bisa jauh lebih pendek daripada data input.
Sudah melihat grafik tampilan interval pada Gambar. 7, kita dapat membuat asumsi bahwa jika intervalnya 2, 4, 6, dll. muncul lebih awal daripada interval, katakanlah, 100, 102, 104, dll., maka yang pertama harus terus terjadi lebih sering daripada yang terakhir. Dan sebaliknya - jika interval 514 hanya mulai dari 11,99 miliar, 516 - mulai dari 16,2 miliar, dan 518 - umumnya mulai hanya 87,7 miliar, maka mereka akan jarang bertemu. Yaitu, apriori, kita dapat mengasumsikan hubungan terbalik antara ukuran interval dan frekuensinya dalam urutan bilangan prima. Dan itu berarti - Anda dapat membangun struktur sederhana yang mengimplementasikan kode panjang variabel untuknya.
Tentu saja, statistik pada frekuensi interval harus menjadi penentu pilihan metode pengkodean tertentu. Untungnya, berbeda dengan data yang berubah-ubah, frekuensi interval antara bilangan prima - yang dengan sendirinya ditentukan secara ketat, sekali dan untuk semua urutan yang diberikan - juga ditentukan secara ketat, sekali dan untuk semua karakteristik yang ditentukan.
Gambar 7 menunjukkan respons frekuensi interval untuk seluruh daftar 1TPrimo:
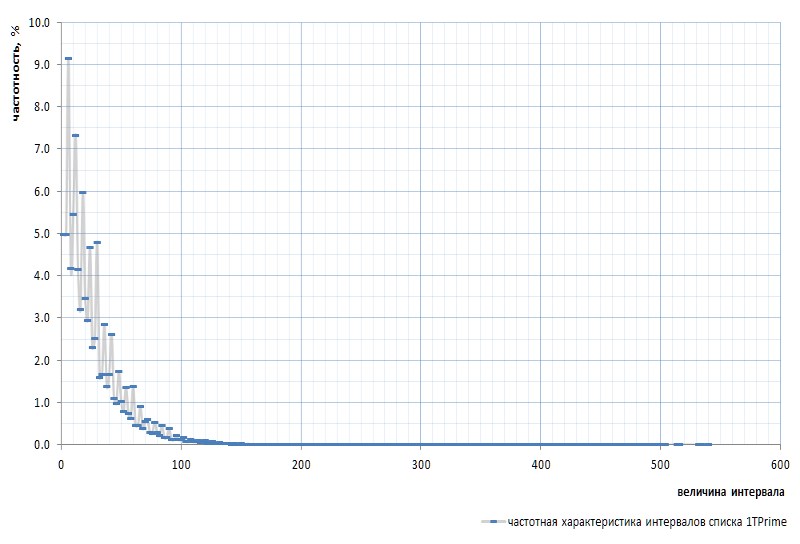
Di sini perlu disebutkan lagi bahwa interval antara bilangan prima pertama 2 dan 3 dikeluarkan dari grafik: interval ini adalah 1 dan terjadi tepat sekali dalam urutan bilangan prima, terlepas dari kekuatan daftar. Interval ini sangat aneh sehingga lebih mudah untuk menghapus 2 dari daftar yang sederhana daripada terus-menerus menyimpang ke reservasi. Sim dinyatakan bahwa nomor 2 adalah virtual prime : tidak terlihat dalam daftar, tetapi ada di sana. Seperti gopher itu.
Pada pandangan pertama, grafik frekuensi sepenuhnya menegaskan asumsi a priori yang diberikan oleh beberapa paragraf di atas. Ini jelas menunjukkan heterogenitas statistik dari interval dan frekuensi tinggi dari nilai-nilai kecil dibandingkan dengan yang besar. Namun, pada tampilan kedua, lebih cembung, grafik ternyata jauh lebih menarik (Gbr. 8):
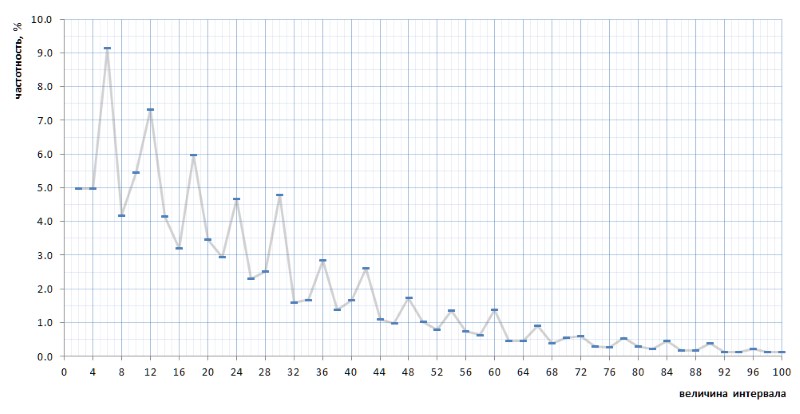
Secara tak terduga, ternyata interval yang paling sering bukan 2 dan 4, seperti yang tampaknya dari pertimbangan umum, tetapi 6, 12 dan 18, diikuti oleh 10 - dan hanya kemudian 2 dan 4 dengan frekuensi yang hampir sama (perbedaan dalam 7 digit). setelah titik desimal). Dan selanjutnya, banyaknya nilai puncak dari angka 6 ditelusuri ke seluruh grafik.
Yang lebih menarik, sifat grafik yang tidak sengaja terungkap ini bersifat universal - dan, dalam semua detail, dengan semua kekusutannya - di atas seluruh urutan interval sederhana yang diwakili oleh daftar 1TPrimo, kemungkinan grafik itu bersifat universal untuk setiap urutan interval sederhana (tentu saja, pernyataan berani seperti itu perlu bukti, yang dengan senang hati saya pindahkan ke pangkat spesialis dalam teori bilangan). Gambar 10 menunjukkan perbandingan statistik interval penuh (garis merah) dengan sampel interval terbatas diambil di beberapa tempat acak pada daftar 1TPrimo (garis warna lain):
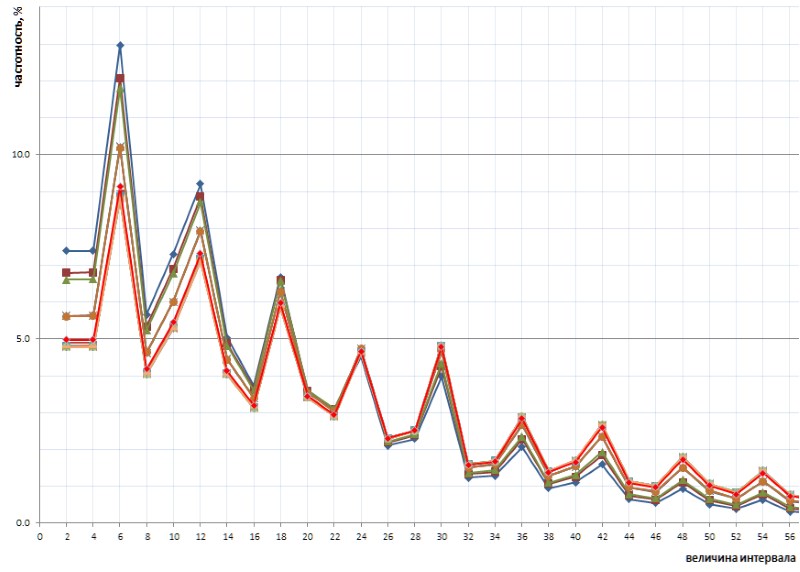
Dapat dilihat dari grafik ini bahwa semua sampel ini saling mengulang dengan tepat, dengan hanya sedikit perbedaan di bagian kiri dan kanan gambar: mereka tampaknya sedikit diputar berlawanan arah jarum jam di sekitar titik interval dengan nilai 24. Rotasi ini mungkin disebabkan oleh fakta bahwa semakin tinggi di sebelah kiri bagian dari grafis dibangun di atas sampel dengan kedalaman bit yang lebih rendah. Dalam sampel seperti itu, belum ada sama sekali, atau interval besar jarang terjadi, yang menjadi sering terjadi pada sampel dengan kedalaman bit yang lebih tinggi. Dengan demikian, ketidakhadiran mereka mendukung frekuensi interval dengan nilai yang lebih rendah. Dalam sampel dengan kedalaman bit yang lebih tinggi, banyak interval baru dengan nilai besar muncul, oleh karena itu, frekuensi interval yang lebih kecil sedikit menurun. Kemungkinan besar, titik pivot, dengan peningkatan kekuatan daftar, akan bergeser ke nilai yang lebih besar. Di suatu tempat di sana, di sebelahnya, adalah titik keseimbangan grafik, di mana jumlah semua nilai di sebelah kanan kira-kira sama dengan jumlah semua nilai di sebelah kiri.
Sifat yang menarik dari frekuensi interval ini menunjukkan meninggalkan struktur sepele dari kode dengan panjang variabel. Biasanya, struktur seperti itu terdiri dari paket bit dengan panjang dan tujuan yang beragam. Sebagai contoh, pertama datang sejumlah bit awalan yang ditetapkan ke nilai tertentu, misalnya, 0. Ada bit stop di belakangnya, yang harus mengindikasikan penyelesaian awalan, dan, karenanya, harus berbeda dari awalan: 1 dalam kasus ini. Awalan mungkin tidak memiliki panjang, yaitu, berulang-ulang, pengambilan sampel dapat segera dimulai dengan stop bit, sehingga menentukan urutan terpendek. Bit stop biasanya diikuti oleh sufiks, yang panjangnya ditentukan dalam beberapa cara yang telah ditentukan oleh panjang awalan. , , — . , - . - (, , - ) , .
, .
Dan di sini satu hal lagi yang penting harus dinyatakan. Pada pandangan pertama, siklus yang diamati menyiratkan pembagian interval menjadi tiga kali lipat: {2,4, 6 } , {8,10, 12 } , {14,16, 18 } dan seterusnya (nilai-nilai dengan frekuensi maksimum di setiap tiga ditandai dengan huruf tebal) . Namun, pada kenyataannya, siklus di sini sedikit berbeda.
Saya tidak akan mengutip seluruh garis penalaran, yang, pada kenyataannya, tidak ada di sana: itu adalah tebakan yang intuitif, ditambah dengan metode pencacahan pilihan, perhitungan, dan sampel yang memakan waktu beberapa hari secara berselang. Siklus yang diungkapkan sebagai hasilnya terdiri dari enam interval {2,4, 6 ,8,10, 12 } , {14,16, 18 ,20,22, 24 } , {26,28, 30 ,32,34, 36 } dan seterusnya (interval frekuensi maksimum sekali lagi disorot dalam huruf tebal).
Singkatnya, algoritma pengemasan yang diusulkan adalah sebagai berikut.
Membagi interval menjadi enam angka genap memungkinkan kita untuk merepresentasikan setiap interval g dalam bentuk g = i * 12 + t , di mana i adalah indeks dari enam di mana interval ini berada ( i = {0,1,2,3, ...} ) dan t adalah ekor yang mewakili salah satu nilai dari yang didefinisikan secara kaku, terikat, dan identik untuk enam set {2,4,6,8,10,12} . Respons frekuensi indeks yang disorot di atas hampir persis berbanding terbalik dengan nilainya, sehingga logis untuk mengubah indeks enam menjadi struktur sepele dari kode panjang variabel, contoh yang diberikan di atas. Karakteristik frekuensi dari penjepit memungkinkan Anda untuk membaginya menjadi dua kelompok yang dapat dikodekan dengan rantai bit dengan panjang yang berbeda: nilai 6 dan 12, yang paling sering ditemukan, dikodekan dengan satu bit, nilai 2, 4, 8 dan 10, yang lebih jarang ditemui, dikodekan dengan dua bit. Tentu saja, satu bit lagi diperlukan untuk membedakan antara dua opsi ini.
Array yang berisi paket bit dilengkapi dengan bidang tetap yang menentukan nilai awal dari data yang disajikan dalam blok, dan jumlah lain yang diperlukan untuk mengembalikan urutan sederhana atau sederhana dari urutan sederhana dari interval yang disimpan dalam blok.
Selain struktur blok-indeks ini, penggunaan kode-panjang variabel rumit oleh biaya tambahan dibandingkan dengan interval bit tetap.
Saat menggunakan interval ukuran tetap, menentukan blok untuk mencari bilangan prima dengan nomor seri adalah tugas yang cukup sederhana, karena jumlah interval per blok diketahui sebelumnya. Tetapi pencarian solusi sederhana dengan nilai terdekat tidak memiliki solusi langsung. Atau, Anda dapat menggunakan beberapa rumus empiris yang memungkinkan Anda menemukan perkiraan nomor blok dengan interval yang diperlukan, setelah itu Anda harus mencari blok yang diinginkan dengan pencarian lengkap.
Untuk tabel dengan kode panjang variabel, pendekatan yang sama diperlukan untuk kedua tugas: baik untuk mengambil nilai dengan nomor maupun untuk pencarian berdasarkan nilai. Karena panjang kode bervariasi, tidak pernah diketahui sebelumnya berapa banyak perbedaan disimpan dalam blok tertentu, dan di mana blok nilai yang diinginkan terletak. Secara eksperimental ditentukan bahwa dengan ukuran blok 512 byte (yang mencakup beberapa header byte), kapasitas blok dapat naik hingga 10-12 persen dari nilai rata-rata. Blok yang lebih kecil menghasilkan sebaran relatif yang lebih besar. Pada saat yang sama, nilai rata-rata kapasitas blok itu sendiri cenderung perlahan menurun seiring bertambahnya tabel. Pemilihan rumus empiris untuk penentuan blok awal yang tidak akurat untuk mencari nilai yang diinginkan baik dengan jumlah maupun nilai adalah tugas yang tidak sepele. Atau, Anda dapat menggunakan pengindeksan yang lebih kompleks dan canggih.
Faktanya, itu saja.
Di bawah ini, seluk-beluk kompresi tabel utama menggunakan kode panjang variabel dan struktur yang terkait dengannya dijelaskan dengan cara yang lebih formal dan terperinci, dan kode untuk fungsi pengemasan dan interval pembongkaran dalam C diberikan.
Hasilnya
Jumlah data yang diterjemahkan dari Tabel 1TPrimo ke dalam kode panjang variabel, ditambah dengan struktur indeks blok, juga dijelaskan di bawah ini, berjumlah 26.309.295.104 byte (24,5 GB), yaitu, rasio kompresi mencapai 11,4. Jelas, dengan meningkatnya kedalaman bit, rasio kompresi akan meningkat.
Waktu siaran 280 GB dari tabel 1TPrimo dalam format baru adalah 1 jam. Ini adalah hasil yang diharapkan setelah percobaan dengan interval pengemasan menjadi integer byte tunggal. Dalam kedua kasus, terjemahan tabel sumber terutama terdiri dari operasi file dan hampir tidak memuat prosesor (dalam kasus kedua, beban masih lebih tinggi karena kompleksitas komputasi algoritma yang lebih tinggi). Waktu akses data juga tidak jauh berbeda dari interval byte tunggal, tetapi waktu untuk membuka blok penuh dengan ukuran yang sama membutuhkan 1,5 μs, karena kompleksitas algoritma yang lebih tinggi untuk mengekstraksi kode panjang variabel.
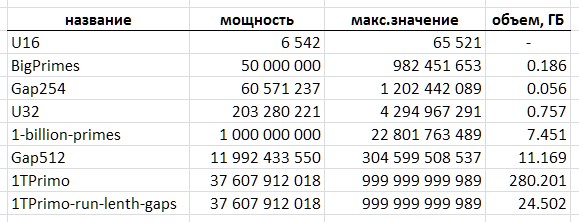
Tabel (Gbr. 10) merangkum karakteristik volumetrik dari tabel bilangan prima yang disebutkan dalam teks ini.
Deskripsi Algoritma Kompresi
Ketentuan dan Notasi
P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 adalah bilangan prima sesuai dengan nomor seri mereka. Sekali lagi (dan untuk terakhir kalinya) saya menekankan bahwa
P0=2 adalah bilangan prima virtual; demi keseragaman formal, angka ini secara fisik dikecualikan dari daftar bilangan prima.
G (gap) - interval antara dua bilangan prima berturut-turut Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...} .
D (dense) - direduksi menjadi interval bentuk monolitik: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} . Enam interval dalam bentuk monolitik terlihat seperti {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} dll.
Q (quotient) - indeks keenam direduksi menjadi bentuk monolitik, Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}
R (remainder) - sisa dari enam monolitik R = D mod 6. R selalu memiliki nilai dalam kisaran {0,1,2,3,4,5} .
Nilai Q dan R diperoleh dengan metode di atas dari sembarang interval G , karena karakteristik frekuensi stabilnya, tunduk pada kompresi dan penyimpanan dalam bentuk paket bit panjang variabel, dijelaskan di bawah ini. Bit string yang menyandikan nilai Q dan R dalam sebuah paket dibuat dengan cara yang berbeda: untuk pengkodean indeks Q , rantai bit dari awalan H , fluks F dan bit bantu S , dan grup bit dari infix X dan bit bantu A digunakan untuk menyandikan sisanya R
A (arbiter) - bit yang menentukan ukuran infiks X : 0 - infiks satu-bit, 1 - dua-bit.
X (infix) - X (infix) 1- atau 2-bit, bersama-sama dengan bit arbiter R cara tabular (tabel juga menunjukkan frekuensi keenam pertama dengan infiks tersebut sebagai referensi):
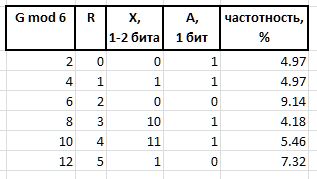
F (fluxion) adalah fluxion, turunan dari indeks Q panjang variabel L={0,1,2...} , yang dirancang untuk membedakan antara semantik string bit (), 0, 00, 000, atau 1, 01, 001 , dll. d.
Rantai bit satuan panjang L dinyatakan sebagai 2^L - 1 (tanda ^ berarti eksponensial). Dalam notasi C, nilai yang sama dapat diperoleh dengan ekspresi 1<<L - 1 . Maka nilai fluksia panjang L dapat diperoleh dari Q ekspresi
F = Q - (1 << L - 1),
dan mengembalikan Q dari fluxia dengan ekspresi
Q = (1 << L - 1) + F.
Sebagai contoh, untuk kuantitas Q = {0..15} , rantai bit fluxia berikut akan diperoleh:
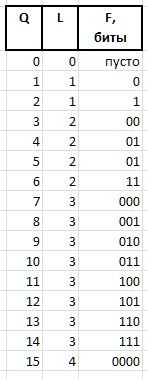
Dua bidang bit terakhir yang diperlukan untuk pengemasan / pengembalian nilai adalah:
H (header) - awalan, serangkaian bit diatur ke 0.
S (stop) - berhenti bit yang diatur ke 1, mengakhiri awalan.
Bahkan, bit ini diproses terlebih dahulu dalam string bit, mereka memungkinkan Anda untuk menentukan selama membongkar atau mengatur selama pengemasan ukuran fluks dan awal bidang arbiter dan fluks - segera setelah bit berhenti.
W (width) - lebar seluruh kode dalam bit.
Struktur lengkap dari paket bit ditunjukkan pada Gambar. 11:
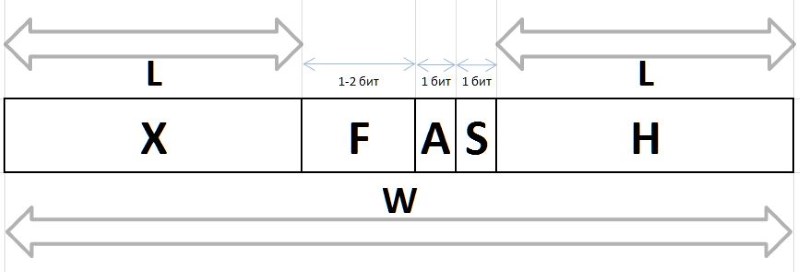
Nilai-nilai Q dan R pulih dari rantai ini memungkinkan kami untuk mengembalikan nilai awal interval:
D = Q * 6 + R,
G = (D + 1) * 2,
dan urutan interval yang dipulihkan memungkinkan Anda untuk mengembalikan bilangan prima asli dari nilai dasar blok yang diberikan (seed seed of interval) dengan menambahkan padanya semua interval dari blok yang diberikan secara berurutan.
Untuk bekerja dengan string bit, variabel integer 32-bit digunakan, di mana bit paling signifikan diproses dan setelah menggunakannya, bit digeser ke kiri saat pengemasan atau ke kanan saat membongkar.
Struktur blok
Selain string bit, blok berisi informasi yang diperlukan untuk mengambil atau menambahkan bit, serta untuk menentukan isi blok.
// // typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // : , #define HEADSIZE (8+8+2+2+2) // , #define BODYSIZE (BLOCKSIZE-HEADSIZE) // . // typedef struct { HUGE base; // , HUGE card; // WORD count; // WORD delta; // base+delta = WORD offset; // BYTE body[BODYSIZE]; // } crunch_block; // , put() get() crunch_block block; // . // NB: len/val rev/rel // , , // . static struct tail_t { BYTE len; // S A BYTE val; // , A - S BYTE rev; // BYTE rel; // } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; // BOOL put(int gap) { // 1. int Q, R, L; // (), (), int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } // L val = Q - (1 << L) + 1; // val <<= tails[R].len; val += tails[R].val; // val <<= L; // L += L + tails[R].len; // // 2. val L buffer put_index if (block.offset + L > BODYSIZE * 8) // ! return FALSE; Q = (block.offset / 8); // , R = block.offset % 8; // block.offset += L; // block.count++; // block.delta += gap; if (R > 0) // { val <<= R; val |= block.body[Q]; L += R; } // L = L / 8 + ((L % 8) > 0 ? 1 : 0); // while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } // int get_index; // // int get() { if (get_index >= BODYSIZE * 8) return 0; // int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; // 4 if (val == 0) return -1; // ! int Q, R, L, F, M, len; // , , , , L = 0; while (!(val & 1)) { val >>= 1; L++; } // - if ((val & 3) == 1) // R = (val >> 2) & 1; // else R = ((val >> 2) & 3) + 2; // len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); // F = val & M; // Q = F + M; // return 2 * (1 + (6 * Q + tails[R].rev)); // }
Perangkat tambahan
Jika kita memberi makan basis interval yang diperoleh ke pengarsipan 7-zip yang sama, maka dalam satu setengah jam kerja intensif pada server 8-core, ia berhasil mengompres file input sebesar hampir 5%. Artinya, dalam database interval panjang variabel dari sudut pandang pengarsipan, masih ada beberapa redundansi. Jadi ada alasan untuk berspekulasi sedikit (dalam arti kata yang baik) pada topik lebih lanjut mengurangi redundansi data.
Determinisme mendasar dari urutan interval antara bilangan prima memungkinkan untuk membuat perhitungan yang tepat dari efisiensi pengkodean dengan satu metode atau yang lain. Secara khusus, sketsa-sketsa kecil (dan agak kacau-balau) memungkinkan untuk menarik kesimpulan mendasar tentang kelebihan pengkodean sixes atas triples, dan tentang kelebihan metode yang diusulkan dibandingkan kode-kode sepele dengan panjang variabel (Gbr. 12):
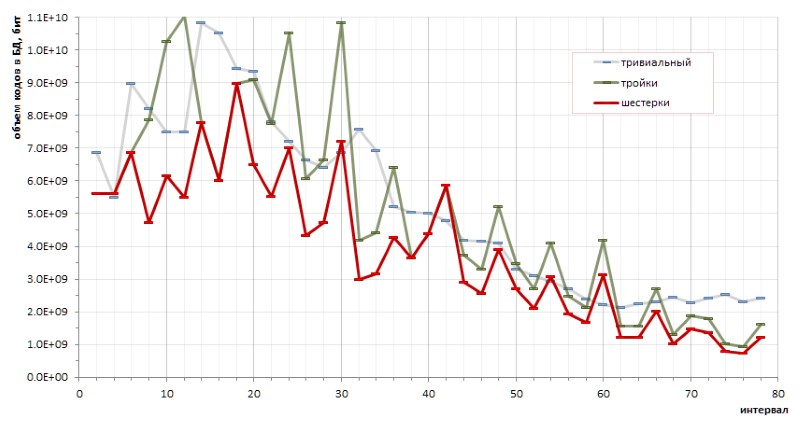
Namun, tingginya grafik merah yang menjengkelkan secara transparan mengisyaratkan bahwa mungkin ada metode penyandian lain yang akan membuat grafik lebih lembut.
Arah lain menyarankan memeriksa frekuensi interval berurutan. Dari pertimbangan umum: karena interval 6, 12, dan 18 adalah yang paling umum dalam populasi bilangan prima, maka mereka cenderung lebih sering ditemukan berpasangan (doublet), triples (triplet), dan kombinasi interval yang serupa. Jika pengulangan duplets (dan bahkan mungkin kembar tiga ... yah, tiba-tiba!) Ternyata secara statistik signifikan dalam massa total interval, maka masuk akal untuk menerjemahkannya ke dalam beberapa kode terpisah.
Eksperimen skala penuh tidak mengungkapkan dominasi tertentu dari doublet individu atas yang lain. Namun, jika kepemimpinan absolut diharapkan untuk pasangan (6,6) - 1.37% dari semua doublet - maka pemenang lain dari peringkat ini jauh kurang jelas:
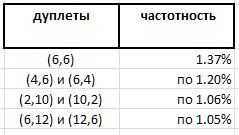
Dan, karena doublet (6,6) simetris, dan semua doublet yang dicatat lainnya asimetris dan ditemukan dalam pemeringkatan oleh mirror ganda dengan frekuensi yang sama, tampaknya catatan rekaman doublet (6,6) dalam seri ini harus dibagi dua di antara dua ganda yang tidak dapat dibedakan (6,6) dan (6,6) , yang membawa mereka 0,68% jauh ke batas daftar hadiah. Dan ini sekali lagi menegaskan pengamatan bahwa tidak ada dugaan benar tentang bilangan prima dapat terjadi tanpa kejutan.
Statistik kembar tiga juga menunjukkan kepemimpinan interval tiga kali lipat seperti itu, yang tidak cukup sesuai dengan asumsi spekulatif yang dimulai dari frekuensi tertinggi interval 6, 12, 18. Dalam menurunkan urutan popularitas, pemimpin frekuensi di antara kembar tiga terlihat sebagai berikut:

dll.
Saya takut, bagaimanapun, bahwa hasil spekulasi saya akan kurang menarik bagi programmer daripada untuk ahli matematika, mungkin karena koreksi tak terduga yang dilakukan oleh praktek menjadi tebakan intuitif. Kecil kemungkinan bahwa akan mungkin untuk mengeluarkan dividen substansial dari persen frekuensi yang disebutkan demi peningkatan rasio kompresi lebih lanjut, sementara kompleksitas algoritme mengancam untuk tumbuh sangat signifikan.
Keterbatasan
Telah dicatat di atas bahwa peningkatan nilai maksimum interval sehubungan dengan kapasitas bilangan prima sangat, sangat lambat. Secara khusus, dapat dilihat dari Gambar. 6 bahwa interval antara bilangan prima yang dapat direpresentasikan dalam format integer unsigned 64-bit jelas akan kurang dari 1600.
Implementasi yang dijelaskan memungkinkan Anda untuk mengemas dan membongkar nilai interval 18-bit dengan benar (pada kenyataannya, kesalahan kemasan pertama terjadi dengan interval input 442358). Saya tidak memiliki imajinasi yang cukup untuk menganggap bahwa basis data interval prima dapat tumbuh ke nilai-nilai seperti itu: begitu saja ada di suatu tempat di sekitar bilangan bulat 100-bit, dan untuk menghitung lebih tepatnya kemalasan. Dalam kasus kebakaran, memperluas rentang interval pada waktu-waktu tertentu tidak akan sulit.
Terima kasih sudah membaca tempat ini :)