Artikel ini membahas penggunaan perpustakaan geometri fungsi WebGeometry untuk membangun model polyhedra kompleks. Perpustakaan ditulis dalam Javascript.
Tautan ke GitHub dengan contoh yang memberikan contoh sederhana menggunakan perpustakaan. Komentar dan kritik dipersilahkan.
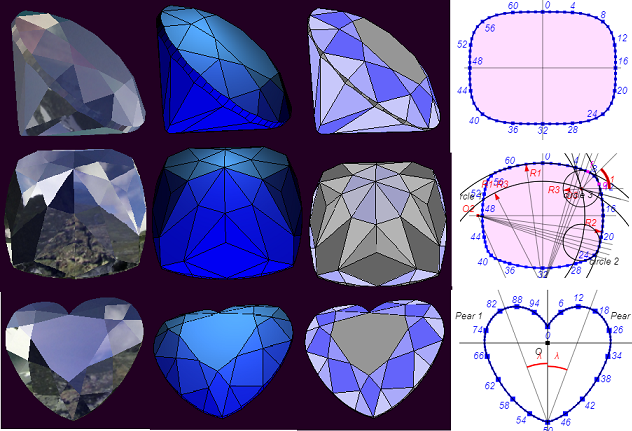
Pustaka ThreeJS digunakan untuk menampilkan model yang dihitung sebelumnya menggunakan fungsi dari pustaka WebGeometry. Kanvas HTML5 digunakan untuk menampilkan elemen model flat individual dan menampilkan informasi pendukung.
Teknologi dan perpustakaan WebGL yang dibuat atas dasar, seperti ThreeJS dan BadylonJS, digunakan di Internet untuk mengimplementasikan berbagai tujuan yang berkaitan dengan grafik 3D. Tetapi pada dasarnya mereka digunakan untuk menampilkan model tiga dimensi siap pakai di browser (yang sebelumnya dibuat, misalnya, dalam
3ds Max atau program
Blender ). Jika kita dihadapkan dengan tugas membuat model parametrik, yaitu model yang, dalam proses menampilkan objek jadi di browser, kita dapat mengubah elemen individu dengan menetapkan parameter model yang sesuai (misalnya, meningkatkan sudut wajah tertentu), kita harus memiliki satu set fungsi geometris yang akan memungkinkan Anda untuk membuat model sehingga di masa depan ada kemungkinan memvariasikan secara interaktif bentuk elemen individu dari model atau keseluruhan model. Untuk mengatasi masalah ini, kita memerlukan satu set fungsi dalam bahasa Javascript yang akan mengimplementasikan metode yang digunakan dalam geometri analitik. Perpustakaan harus memiliki fungsi untuk membuat garis, bidang dan lingkaran, menemukan titik (atau garis) dari persimpangan mereka, membuat bidang miring, dan banyak lagi. Pustaka ThreeJS dan BadylonJS memiliki beberapa fitur ini, tetapi jumlah tindakan yang dilakukan dengannya tidak akan memungkinkan Anda untuk menyelesaikan semua tugas yang muncul saat membangun model parametrik. Ada beberapa perpustakaan Javascript yang lebih murni matematika. Dari jumlah tersebut,
glMatrix dan
Sylvester paling banyak digunakan. Pustaka
glMatrix terutama ditujukan untuk bekerja dengan vektor, matriks, dan angka empat, tetapi tidak ada fungsi untuk bekerja dengan garis dan bidang di dalamnya. Perpustakaan
Sylvester memiliki fungsi-fungsi ini, tetapi mereka hadir dalam jumlah yang agak terbatas. Namun, ada beberapa buku yang menggambarkan implementasi metode geometri analitik dalam C / C ++. Program C / C ++ yang sesuai dapat digunakan sebagai prototipe untuk membuat perpustakaan matematika dalam Javascript. Oleh karena itu, ketika saya memutuskan untuk membuat model parametrik tiga dimensi potongan berlian untuk menampilkannya di browser, perpustakaan ThreeJS dipilih oleh saya hanya untuk menampilkan model yang sudah dihitung - itu tidak digunakan untuk menghitung bentuk model. Untuk perhitungan formulir itu sendiri, perpustakaan WebGeometry dibuat. Pustaka ini didasarkan pada fungsi geometrik yang sebelumnya digunakan dalam C / C ++, yang saya terjemahkan ke dalam bahasa Javascript. Mari kita perhatikan tahapan membangun model piramida (pemotongan berlian tipe Piramida).
Pada
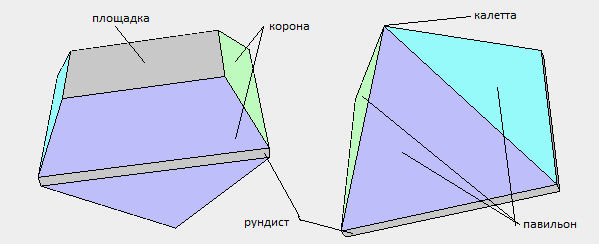
tahap pertama, kita perlu menggambar tampilan yang diinginkan dari model dan kemudian nomor simpulnya. Gambar di bawah ini menunjukkan penomoran simpul dan nama elemen potong yang termasuk dalam model potongan piramida.

Setelah itu, diperlukan untuk membentuk wajah dari simpul bernomor. Misalnya, untuk wajah situs dan wajah mahkota, tulis urutan simpul berikut (simpul pertama yang diduplikasi memberi sinyal bahwa wajah telah berakhir):
0, 3, 2, 1, 0;
Wajah harus berlawanan arah jarum jam. File pyramid_index.js berisi kode sumber untuk melintasi semua wajah piramida dan komentar terperinci. Hasil perayapan ditulis ke array index_cut.
Pada
tahap kedua, kita bisa mewarnai wajah model. Langkah ini opsional jika kita tidak membutuhkan pewarnaan. Misalkan kita ingin mewarnai model piramida sebagai berikut:
Untuk tujuan ini, file pyramid_colors.js dibuat di mana fungsi facet_colors () berada, yang menulis warna semua wajah ke array warna.
Pada
tahap ketiga , setelah semua simpul diberi nomor dan urutan traversal dari semua simpul dari wajah dicatat, perlu untuk mengatur parameter model dan kemudian menghitung koordinat semua simpulnya. Tentu saja, diasumsikan bahwa kita telah menguraikan algoritma konstruksi untuk diri kita sendiri dan menemukan bagaimana semua wajah model akan ditempatkan di ruang angkasa. Untuk piramida, kita akan memilih parameter berikut, yang akan menentukan ukuran dari masing-masing bagiannya, dan keseluruhan model secara keseluruhan:
var DEGREE = 0.01745329251994;
Pilihan parameter ditentukan oleh pengembang model. Misalnya, alih-alih mengatur dua parameter untuk dua sudut kemiringan mahkota, Anda dapat menentukan parameter tunggal untuk dua sudut sekaligus - maka sudut ini akan selalu sama. Anda dapat memasukkan parameter yang menentukan ukuran situs. Dalam hal ini, diperlukan untuk tidak mengatur tinggi mahkota, atau untuk tidak mengatur kemiringan wajahnya. Pilihan lain untuk memilih parameter adalah membuat beberapa parameter dapat dihitung. Dalam hal ini, ketika mengubah beberapa parameter, beberapa lainnya mungkin mengubah nilai awal mereka. Sebagai contoh, jika kita mengasumsikan bahwa untuk piramida kita telah menentukan satu parameter untuk mengatur sudut kemiringan permukaan koronal, parameter lain untuk ketinggian mahkota dan parameter lain yang akan mengatur ukuran area, maka ketika mengubah sudut wajah kita akan dipaksa untuk mengubah ukuran area atau tinggi mahkota. Di sisi lain, jika Anda mengubah parameter yang menetapkan ukuran pad, maka nilai parameter yang menetapkan tinggi atau kemiringan permukaan koronal akan secara otomatis berubah. Opsi yang terkait dengan penerapan parameter yang dihitung dalam program ini, serta dalam konstruksi model potongan lain yang disajikan di situs, tidak digunakan.
Pada
tahap keempat , koordinat simpul dari model dihitung. Data awal untuk perhitungan adalah nilai-nilai parameter model dan bagaimana kita membayangkan penampilannya. File pyramid_verts.js berisi teks sumber (dengan komentar terperinci) dari fungsi perhitungan vertex model, yang disebut VerticesCalculation. Dengan perhitungan ini bahwa fungsi perpustakaan WebGeometry digunakan dalam fungsi ini. Hasil penghitungan koordinat titik dimasukkan dalam array titik. Perhatikan bahwa dalam program untuk menemukan koordinat simpul, urutan angka yang terpisah digunakan untuk simpul yang membentuk korona (empat simpul), simpul yang membentuk korset (empat simpul) dan simpul yang membentuk paviliun (dalam model piramida, hanya simpul yang termasuk dalam paviliun). Pilihan penomoran verteks tambahan ini digunakan untuk orientasi yang lebih mudah oleh programmer di antara simpul yang terpotong, karena jumlah simpul sangat sering melebihi 100.
Pada
tahap kelima, setelah perhitungan koordinat simpul selesai, diperlukan untuk pemrograman membangun polyhedron (polyhedron) dari model. Data awal untuk konstruksinya adalah susunan index_cut, warna, dan simpul yang sebelumnya dibuat. Model polyhedron dapat direpresentasikan secara sederhana sebagai satu set wajah yang mengikat polyhedron di ruang angkasa. Fungsi CreatePolyhedron ada di file polyhedron.js. Sebagai hasil dari pekerjaan fungsi ini, array poligon (poligon) dibuat yang terdiri dari model tiga dimensi. Setiap poligon dijelaskan oleh fungsi berikut (pada kenyataannya, ini adalah fungsi konstruktor yang dipanggil oleh operator baru saat membuat poligon baru):
function Polygon() { this.IndexFacet = [];
Karena WebGL dan pustaka ThreeJS dibuat berdasarkan kerjanya dengan primitif triangular, ia di-triangulasi untuk setiap sisi model. Diasumsikan bahwa semua wajah model adalah poligon cembung. Pada akhirnya, fungsi CreatePolyhedron mengambil semua langkah yang diperlukan untuk membuat struktur data yang sepenuhnya menggambarkan semua wajah polyhedron sedemikian rupa sehingga mereka dapat diteruskan ke fungsi perpustakaan ThreeJS untuk menampilkan model di layar.
Pada
tahap keenam , model ditampilkan di layar menggunakan fungsi ThreeJS. Secara standar, adegan, renderer, dan kamera dibuat. Untuk memeriksa model potongan dari semua sisi, program Piramida menggunakan elemen orbitControls. Saat membuat model potongan lain, untuk memeriksa potongan dari semua sisi, saya tidak menggunakan orbitControls, tetapi memperkenalkan kemampuan untuk memutar model itu sendiri. Kemudian kami membuat model jerat. Anda dapat melakukan dua hal.
Dalam metode pertama, kami mempertimbangkan model potongan sebagai satu set jerat wajah yang terpisah. Dalam hal ini, setiap wajah adalah objek 3D yang terpisah. Dengan representasi model ini, proses pemilihan wajah individu menggunakan elemen Three.JS, yang memiliki nama raycaster, cukup sederhana. Juga, metode ini dapat dilengkapi dengan pembuatan jerat segmen yang membatasi setiap wajah.
Dengan cara kedua, kami menganggap model potongan sebagai objek tunggal, diwakili oleh hanya satu jala yang segera mencakup semua wajah model. Metode ini nyaman digunakan saat menampilkan model menggunakan shader. Metode ini tidak digunakan dalam model potongan Pyramid, tetapi digunakan untuk membuat Octagon, Brilliant, dan model potongan lainnya yang dapat dilihat di situs web saya.
Pada
tahap ketujuh , tombol dan fungsi yang melekat padanya dibuat yang memungkinkan Anda untuk mengubah nilai parameter yang menentukan bentuk dan ukuran model. Ketika tombol ditekan, fungsi dipanggil yang menambah atau mengurangi nilai parameter yang sesuai. Ini berarti bahwa Anda perlu menghitung ulang koordinat dari simpul model. Setelah penghitungan ulang, kebenaran dari model yang baru dibangun diperiksa. Misalnya, ditentukan apakah beberapa nilai di luar toleransi. Dalam hal model potongan intan, ini biasanya dilakukan untuk memeriksa apakah potongan cembung tetap setelah pembangunan kembali. Memeriksa tonjolan adalah sebagai berikut. Melalui masing-masing wajah pesawat ditarik di mana wajah ini terletak, dan kemudian posisi setiap simpul model relatif terhadap pesawat ini ditentukan. Semua simpul harus terletak di sisi yang sama dari bidang ini. Jika model dianggap salah, maka parameter dikembalikan ke nilai aslinya dan model dibangun kembali. Untuk model potongan yang memiliki korset non-cembung (hanya elemen dari beberapa potongan ini, seperti Jantung, mungkin bukan cembung), cembung diperiksa secara terpisah untuk mahkota dan secara terpisah untuk paviliun. Namun, rundist dikeluarkan dari cek. Untuk model sederhana, Anda dapat membatasi diri pada pemeriksaan parameter sederhana. Sebagai contoh, jika kita membangun model rumah, maka atapnya tidak boleh lebih dari ketinggian tertentu di muka. Oleh karena itu, cukup dengan mengatur batasan parameter ini dalam besarnya, kami memperoleh hasil yang diinginkan. Setelah tombol parameter ditambahkan, sangat diinginkan untuk secara visual menampilkan nilai setiap parameter ketika ia berubah setelah mengklik tombol. Untuk melakukan ini, kanvas dua dimensi HTML5 dibuat dan di sebelah tombol terkait nilai parameter ditampilkan di atasnya.
Dengan demikian, kami memeriksa semua tahap membangun model menggunakan contoh Piramida. Untuk piramida (dan juga untuk semua model lain di situs), saya membuat program lain Pyramid_text.html. Contoh program ini menunjukkan bagaimana Anda dapat menampilkan teks tiga dimensi untuk penomoran simpul suatu model. Jika seseorang ingin tahu bagaimana model rumit dibangun, maka Anda harus mempertimbangkan membangun model
(lihat GitHub) dalam urutan berikut:
Octagon . Model yang menunjukkan penciptaan pesawat dengan berbagai cara dan bekerja dengan pesawat ini. Saat membuat model, metode yang digunakan saat bekerja dengan vektor dan garis dalam ruang juga digunakan.
Cemerlang . Ini adalah potongan berlian klasik dan paling umum. Beberapa elemen membangun model tiga dimensi dari potongan ini digunakan di masa depan ketika membuat aspek MoonMarquise, MoonPear dan Heart. Bagaimana korset potongan ini, yang memiliki bentuk superellipse, dihitung, ditampilkan secara terpisah di program BrilliantGirdlt.html. Dalam program ini, garis korset dibangun di atas kanvas dua dimensi (kanvas).
MoonMarquise . Potongan marquise, seperti Brilliant, adalah salah satu potongan berlian klasik. Tidak seperti sisi sederhana dari tipe ini (Marquise), yang disebut "aspek bulan" ditambahkan ke sisi MoonMarquise Pavilion. Pemotong MoonMarquise dibentuk oleh dua busur elips. Konstruksi rinci korset ini di atas kanvas ditampilkan dalam program MarquiseGirdle.html. Teks program ini memiliki komentar terperinci tentang konstruksi. Kami mencatat satu titik mengenai perhitungan garis korset - ia menggunakan properti garis singgung ke elips. Misalnya, dianggap dalam buku "Kursus Geometri Analitik" (penulis buku ini adalah N.I. Muskhelishvili).
MoonPear Kerapu potong MoonPear dibentuk oleh busur tiga elips. Pembangunannya didasarkan pada konstruksi korset potongan Marquise, tetapi lebih kompleks. Untuk melihat garis korset Marquise dan cara membagi gundist menjadi segmen, jalankan program PearGirdle.html.
Hati Potongan "hati" adalah salah satu potongan klasik, tetapi memiliki, berbeda dengan sebagian besar jenis potongan, bentuk korset non-cembung. Rudist potongan jantung terdiri dari dua girdle cut Pear yang dimiringkan satu sama lain. Di kanvas, Anda dapat melihat garis korset dengan menjalankan program HeartGirdle.html. Membangun luka Jantung cukup sulit.
Maltese Cross . Pemotong potongan "Maltese Cross" dibuat dalam bentuk "bantal" (bantal). Stek dengan korset seperti itu baru-baru ini menyebar luas. Garis korset ini terdiri dari delapan lingkaran konjugasi lingkaran - empat busur utama yang membatasi bantal di empat sisi dan empat busur berukuran lebih kecil yang berpasangan dengan busur utama bantal di sudut-sudut korset. Dengan menjalankan program CushionGirdle_1.html dan CushionGirdle_2.html, Anda dapat melihat bentuk garis korset, hasil kerja dari semua parameter yang menentukan bentuknya dan pembagian korset ke dalam segmen.
Bintang Pentagonal . Pemotong bintang pentagonal dibentuk oleh garis bertuliskan nama epitrochoid. Epitrochoid adalah kurva yang berhubungan dengan sikloid. Dalam program Wavy_Pentagon_Girdle.html, dengan mengubah nilai-nilai parameter, Anda dapat mengubah "undulasi" korset dan bahkan mengubah pentagon menjadi poligon dengan jumlah tonjolan yang berbeda ("kelopak"). Namun, harus diingat bahwa model potongan ini sendiri dibangun untuk nilai parameter "Jumlah kelopak" sama dengan 5.
Seperti yang disebutkan sebelumnya, untuk semua model di atas, program dibuat menampilkan jumlah simpul potong. Dalam program ini, saklar dibuat antara tampilan seluruh simpul dari model dan indikasi nomor simpul untuk mahkota, korset dan paviliun secara terpisah. Misalkan dalam model potongan Malta Anda ingin membuat pesawat melewati simpul dengan angka 84, 88 dan 145. Alih-alih menggunakan angka-angka ini untuk mengidentifikasi titik-titik di mana pesawat melewati ketika membuat pesawat menggunakan fungsi CreatePlaneThreePoints, rekaman menggunakan terpisah penomoran puncak untuk korset dan paviliun:
var plane = new Plane3D(); plane.CreatePlaneThreePoints(girdle[68], girdle[72], crown[1]);
Perlu dicatat bahwa program yang menampilkan nomor model simpul bekerja sangat lambat (setidaknya di komputer saya). Mungkin diperlukan beberapa detik sebelum output dari nomor model titik selesai.
Untuk meringkas semua hal di atas, menurut pendapat saya, pilihan polyhedra (model potong) untuk mendemonstrasikan operasi fungsi geometrik adalah salah satu pilihan terbaik. Setelah memeriksa karya contoh-contoh di atas, kita dapat melanjutkan ke penciptaan objek geometris yang terkait dengan bidang aktivitas yang sama sekali berbeda dari pemodelan pemotongan berlian.