Geekly articles weekly

Solusi numerik dari model matematika objek yang diberikan oleh sistem persamaan diferensial

Pendahuluan:


Dalam pemodelan matematika dari sejumlah perangkat teknis, sistem persamaan nonlinier diferensial digunakan. Model seperti itu digunakan tidak hanya dalam teknologi, mereka digunakan dalam ekonomi, kimia, biologi, kedokteran, dan manajemen.

Studi tentang fungsi alat-alat tersebut membutuhkan solusi dari sistem persamaan ini. Karena sebagian besar persamaan tersebut nonlinier dan tidak stasioner, seringkali mustahil untuk mendapatkan solusi analitiknya.

Ada kebutuhan untuk menggunakan metode numerik, yang paling terkenal adalah metode Runge - Kutta [1]. Adapun Python, dalam publikasi tentang metode numerik, misalnya [2,3], ada sangat sedikit data tentang penggunaan Runge - Kutta, dan tidak ada data tentang modifikasi pada metode Runge - Kutta - Felberg.

Saat ini, berkat antarmuka yang sederhana, fungsi odeint dari modul scipy.integrate memiliki distribusi terbesar di Python. Fungsi kedua dari modul ini mengimplementasikan beberapa metode, termasuk metode Runge-Kutta-Felberg lima peringkat yang disebutkan, tetapi karena sifatnya yang universal, kinerjanya terbatas.

Tujuan dari publikasi ini adalah analisis komparatif dari sarana yang terdaftar untuk menyelesaikan sistem persamaan diferensial secara numerik dengan penulis yang dimodifikasi di bawah Python menggunakan metode Runge-Kutta-Felberg. Publikasi ini juga menyediakan solusi untuk masalah nilai batas untuk sistem persamaan diferensial (SDE).

Data teoritis dan aktual singkat tentang metode dan perangkat lunak yang dipertimbangkan untuk solusi numerik CDS


Masalah Cauchy

Untuk satu persamaan diferensial dari urutan ke-n, masalah Cauchy terdiri dalam menemukan fungsi yang memenuhi kesetaraan:



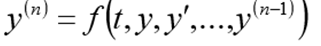
dan kondisi awal



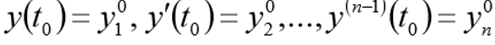
Sebelum menyelesaikan masalah ini harus ditulis ulang dalam bentuk CDS berikut

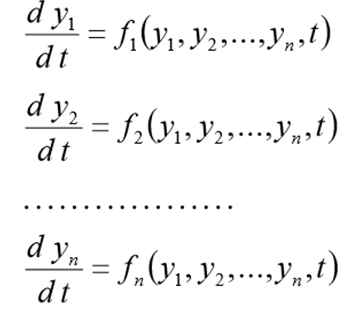
(1)

dengan kondisi awal



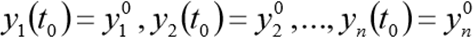Modul Scipy.integrate

Modul ini memiliki dua fungsi ode () dan odeint (), yang dirancang untuk menyelesaikan sistem persamaan diferensial biasa (ODEs) dari urutan pertama dengan kondisi awal pada satu titik (masalah Cauchy). Fungsi ode () lebih universal, dan fungsi odeint () (ODE integrator) memiliki antarmuka yang lebih sederhana dan menyelesaikan sebagian besar masalah dengan baik.

Odeint () berfungsi

Fungsi odeint () memiliki tiga argumen yang diperlukan dan banyak opsi. Ini memiliki format berikut odeint (func, y0, t [, args = (), ...]) func func adalah nama Python dari fungsi dua variabel, yang pertama adalah daftar y = [y1, y2, ..., yn ], dan yang kedua adalah nama variabel independen.

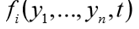
Fungsi fungsi harus mengembalikan daftar nilai fungsi n untuk nilai yang diberikan dari argumen independen t. Faktanya, fungsi func (y, t) mengimplementasikan perhitungan sisi kanan sistem (1).

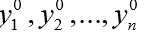
Argumen kedua y0 dari odeint () adalah array (atau daftar) dari nilai awal pada t = t0.

Argumen ketiga adalah berbagai titik waktu di mana Anda ingin mendapatkan solusi untuk masalah tersebut. Dalam hal ini, elemen pertama dari array ini dianggap sebagai t0.

Fungsi odeint () mengembalikan array ukuran len (t) x len (y0). Fungsi odeint () memiliki banyak opsi yang mengontrol operasinya. Opsi rtol (kesalahan relatif) dan atol (kesalahan absolut) menentukan kesalahan perhitungan ei untuk setiap nilai yi sesuai dengan rumus



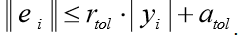
Mereka bisa menjadi vektor atau skalar. Secara default



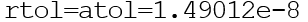Ode () berfungsi

Fungsi kedua dari modul scipy.integrate, yang dirancang untuk menyelesaikan persamaan dan sistem diferensial, disebut ode (). Itu menciptakan objek ODE (ketik scipy.integrate._ode.ode). Memiliki tautan ke objek seperti itu, orang harus menggunakan metode-metodenya untuk menyelesaikan persamaan diferensial. Serupa dengan fungsi odeint (), fungsi odeint (func) melibatkan pengurangan masalah ke sistem persamaan diferensial dari bentuk (1) dan menggunakan fungsinya di sisi kanan.

Satu-satunya perbedaan adalah bahwa fungsi sisi kanan func (t, y) menerima variabel independen sebagai argumen pertama, dan daftar nilai fungsi yang diinginkan sebagai yang kedua. Misalnya, urutan instruksi berikut ini membuat ODE yang mewakili tugas Cauchy.

Metode Runge - Kutta

Ketika membangun algoritma numerik, kami mengasumsikan bahwa solusi untuk masalah diferensial ini ada, itu unik dan memiliki sifat kelancaran yang diperlukan.

Dalam solusi numerik masalah Cauchy

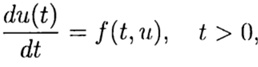
(2)

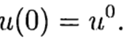
(3)

menurut solusi yang diketahui pada titik t = 0, perlu untuk menemukan solusi dari persamaan (3) untuk t lainnya. Dalam solusi numerik masalah (2), (3), kita akan menggunakan kotak seragam, untuk kesederhanaan, dalam variabel t dengan langkah t> 0.

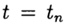
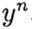
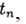
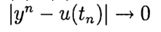
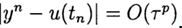
Solusi perkiraan untuk masalah (2), (3) pada intinya menunjukkan . Metode bertemu pada satu titik jika di . Metode ini memiliki urutan akurasi ke-6 jika , p> 0 untuk . Skema perbedaan paling sederhana untuk solusi perkiraan untuk masalah (2), (3) adalah

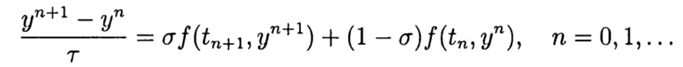
(4)

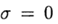
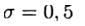
Di kami memiliki metode eksplisit dan dalam hal ini skema perbedaan mendekati persamaan (2) dengan urutan pertama. Desain simetris dalam (4) memiliki urutan aproksimasi kedua. Skema ini milik kelas implisit - untuk menentukan solusi perkiraan pada layer baru, perlu untuk menyelesaikan masalah nonlinier.

Lebih mudah untuk membangun skema pendekatan tingkat kedua dan tingkat atas yang eksplisit berdasarkan metode prediktor-korektor. Pada tahap prediktor (prediksi), skema eksplisit digunakan.

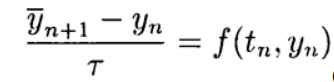
(5)

dan pada tahap korektor (penyempurnaan), diagram



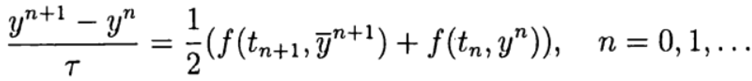
Dalam metode Runge - Kutta satu langkah, gagasan prediktor-korektor diwujudkan sepenuhnya. Metode ini ditulis dalam bentuk umum:

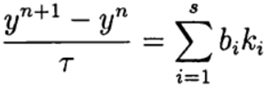
(6)

dimana



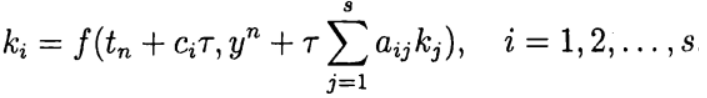
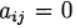
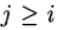
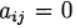
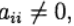
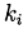
Formula (6) didasarkan pada perhitungan s dari fungsi f dan disebut s-stage. Jika di kami memiliki metode Runge - Kutta yang eksplisit. Jika untuk j> 1 dan lalu ditentukan secara implisit dari persamaan:

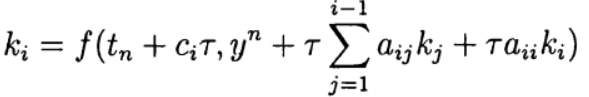
(7)

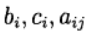
Metode Runge - Kutta ini dikatakan implisit secara diagonal. Parameter tentukan varian dari metode Runge - Kutta. Representasi metode berikut digunakan (Butcher table)



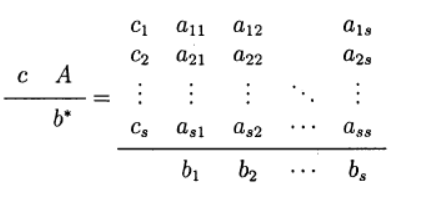
Salah satu yang paling umum adalah metode Runge - Kutta eksplisit urutan keempat.

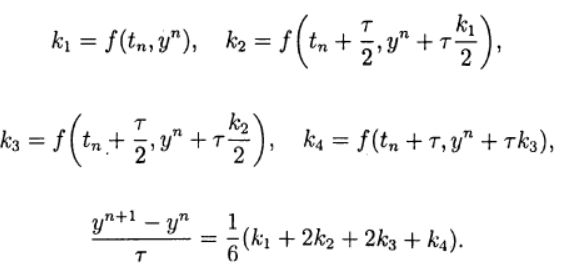
(8)

Metode Runge - Kutta - Felberg

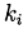
Saya memberikan nilai dari koefisien yang dihitung metode

(9)

Mengingat (9), solusi umum memiliki bentuk:

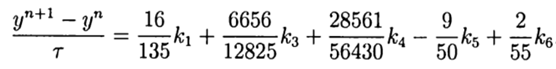
(10)

Solusi ini memberikan urutan ke lima akurasi, tetap menyesuaikannya dengan Python.

Percobaan komputasi untuk menentukan kesalahan absolut dari solusi numerik dari persamaan diferensial nonlinear 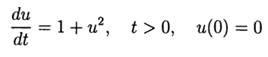menggunakan kedua fungsi def odein (), def oden () dari modul scipy.integrate dan metode Runge - Kutta dan Runge - Kutta - Felberg diadaptasi ke Python



Daftar program
from numpy import* import matplotlib.pyplot as plt from scipy.integrate import * def odein(): #dy1/dt=y2 #dy2/dt=y1**2+1: def f(y,t): return y**2+1 t =arange(0,1,0.01) y0 =0.0 y=odeint(f, y0,t) y = array(y).flatten() return y,t def oden(): f = lambda t, y: y**2+1 ODE=ode(f) ODE.set_integrator('dopri5') ODE.set_initial_value(0, 0) t=arange(0,1,0.01) z=[] t=arange(0,1,0.01) for i in arange(0,1,0.01): ODE.integrate(i) q=ODE.y z.append(q[0]) return z,t def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau): if z==1: k0 =tau* f(t,y) k1 =tau* f(t+tau/2.,y+k0/2.) k2 =tau* f(t+tau/2.,y+k1/2.) k3 =tau* f(t+tau, y + k2) return (k0 + 2.*k1 + 2.*k2 + k3) / 6. elif z==0: k1=tau*f(t,y) k2=tau*f(t+(1/4)*tau,y+(1/4)*k1) k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2) k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3) k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4) k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5) return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6 t = [] y= [] t.append(to) y.append(yo) while to < tEnd: tau = min(tau, tEnd - to) yo = yo + increment(f, to, yo, tau) to = to + tau t.append(to) y.append(yo) return array(t), array(y) def f(t, y): f = zeros([1]) f[0] = y[0]**2+1 return f to = 0. tEnd = 1 yo = array([0.]) tau = 0.01 z=1 t, yn = rungeKutta(f, to, yo, tEnd, tau) y1n=[i[0] for i in yn] plt.figure() plt.title("   (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") plt.plot(t,abs(array(y1n)-array(tan(t))),label=' β€” \n\   -   ') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) z=0 t, ym = rungeKutta(f, to, yo, tEnd, tau) y1m=[i[0] for i in ym] plt.figure() plt.title("   (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") plt.plot(t,abs(array(y1m)-array(tan(t))),label=' β€”β€”  \n\   -   ') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("    (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") y,t=odein() plt.plot(t,abs(array(tan(t))-array(y)),label=' odein') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) plt.figure() plt.title("    (..- u(t)=tan(t)) \n\ du/dt=u**2+1 cu(0)=0  t>0") z,t=oden() plt.plot(t,abs(tan(t)-z),label=' ode  β€”β€”  \n\  ') plt.xlabel('') plt.ylabel(' .') plt.legend(loc='best') plt.grid(True) plt.show()


Kami mendapatkan:









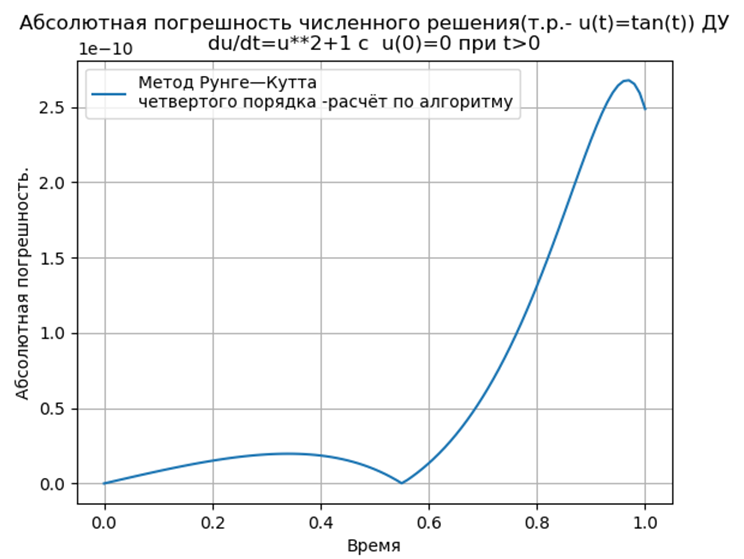
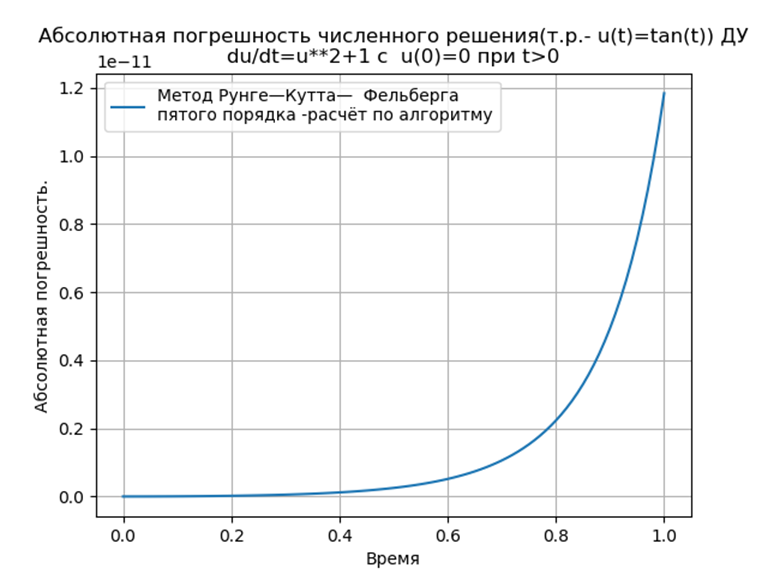
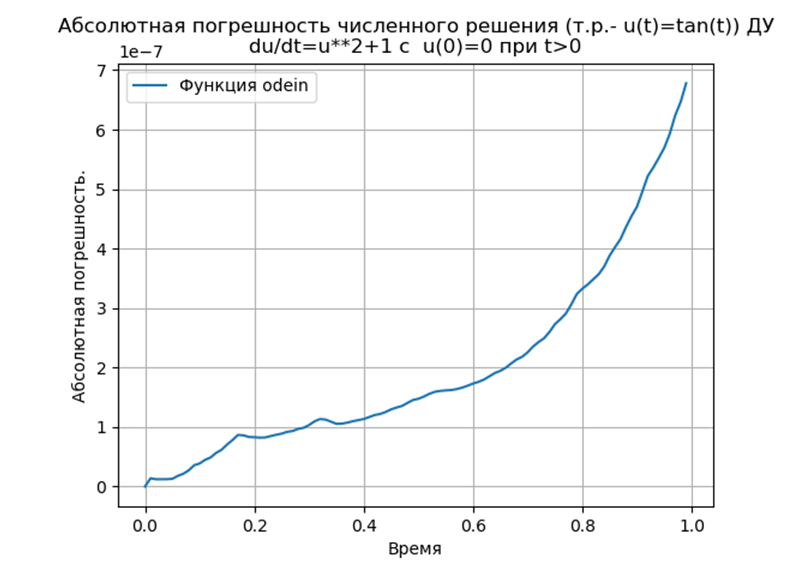
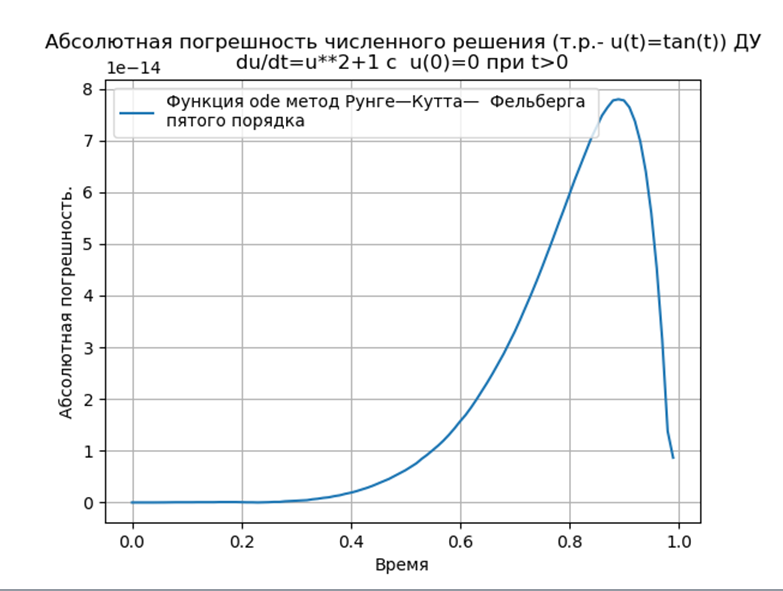Kesimpulan:

Metode Python-adapted Runge - Kutta dan Runge - Kutta - Felberg memiliki absolut yang lebih rendah daripada solusi menggunakan fungsi odeint, tetapi lebih dari solusi menggunakan fungsi edu. Perlu untuk melakukan studi kinerja.

Eksperimen numerik yang membandingkan kecepatan solusi numerik SDE menggunakan fungsi ode dengan atribut dopri5 (metode Runge - Kutta orde 5) dan menggunakan metode Runge - Kutta - Felberg yang disesuaikan dengan Python



Analisis komparatif dilakukan dengan menggunakan masalah model yang diberikan dalam [2] sebagai contoh. Agar tidak mengulangi sumbernya, saya akan menyajikan formulasi dan solusi dari masalah model dari [2].

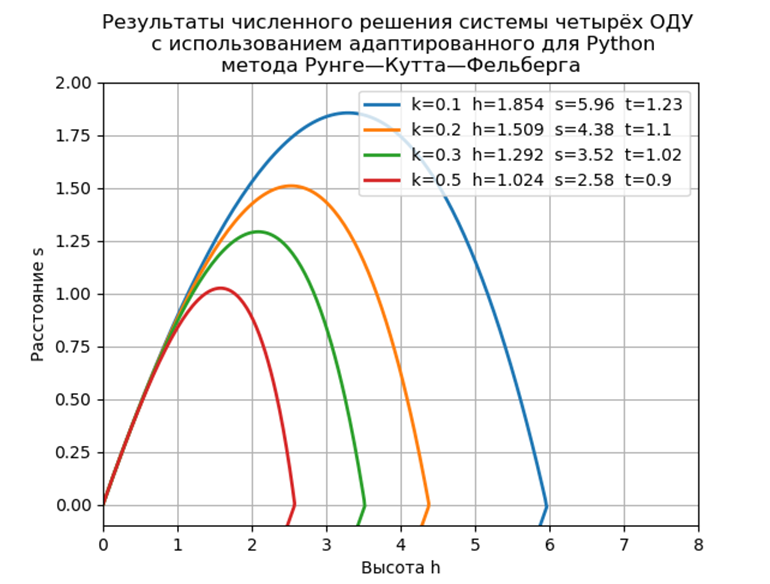
Mari kita selesaikan masalah Cauchy, yang menggambarkan gerakan benda yang dilemparkan dengan kecepatan awal v0 pada sudut Ξ± ke cakrawala dengan asumsi bahwa hambatan udara sebanding dengan kuadrat kecepatan. Dalam bentuk vektor, persamaan gerak memiliki bentuk



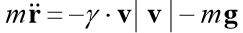
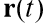
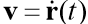
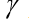
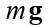
dimana Adalah jari-jari vektor tubuh yang bergerak, Apakah vektor kecepatan tubuh, - koefisien seret, vektor kekuatan berat badan massa m, g - percepatan gravitasi.



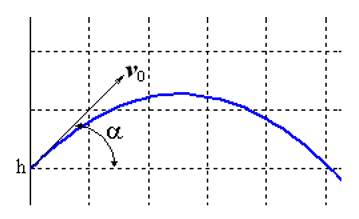
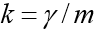
Keunikan dari tugas ini adalah bahwa gerakan berakhir pada titik yang sebelumnya tidak diketahui saat tubuh jatuh ke tanah. Jika ditunjuk , maka dalam bentuk koordinat kami memiliki sistem persamaan:



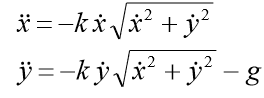
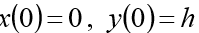
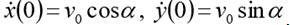
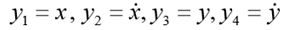
Kondisi awal harus ditambahkan ke sistem: (h ketinggian awal) . Taruh . Kemudian sistem ODE urutan pertama yang sesuai mengambil bentuk:



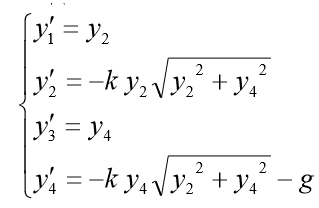
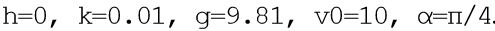
Untuk masalah model yang kami masukkan . Mengabaikan deskripsi yang agak luas dari program ini, saya hanya akan memberikan daftar dari komentar yang, saya pikir, prinsip operasinya akan menjadi jelas. Program ini telah menambahkan hitungan mundur untuk analisis komparatif.

Daftar program
 import numpy as np import matplotlib.pyplot as plt import time start = time.time() from scipy.integrate import ode ts = [ ] ys = [ ] FlightTime, Distance, Height =0,0,0 y4old=0 def fout(t, y):#   global FlightTime, Distance, Height,y4old ts.append(t) ys.append(list(y.copy())) y1, y2, y3, y4 = y if y4*y4old<=0: #    Height=y3 if y4<0 and y3<=0.0: #    FlightTime=t Distance=y1 return -1 y4old=y4 #      def f(t, y, k): #    k g=9.81 y1, y2, y3, y4 = y return [y2,-k*y2*np.sqrt(y2**2+y4**2), y4,-k*y4*np.sqrt(y2**2+y4**2)-g] tmax=1.41 #     alph=np.pi/4 #    v0=10.0 #   K=[0.1,0.2,0.3,0.5] #    y0,t0=[0, v0*np.cos(alph), 0, v0*np.sin(alph)], 0 #   ODE=ode(f) ODE.set_integrator('dopri5', max_step=0.01) ODE.set_solout(fout) fig, ax = plt.subplots() fig.set_facecolor('white') for k in K: #     ts, ys = [ ],[ ] ODE.set_initial_value(y0, t0) #    ODE.set_f_params(k) #    k #   f(t,y,k)     ODE.integrate(tmax) #   print('Flight time = %.4f Distance = %.4f Height =%.4f '% (FlightTime,Distance,Height)) Y=np.array(ys) plt.plot(Y[:,0],Y[:,2],linewidth=3,label='k=%.1f'% k) stop = time.time() plt.title("      \n    ode   dopri5 ") print ("   : %f"%(stop-start)) plt.grid(True) plt.xlim(0,8) plt.ylim(-0.1,2) plt.legend(loc='best') plt.show()



Kami mendapatkan:

Waktu penerbangan = 1.2316 Jarak = 5.9829 Tinggi = 1.8542
Waktu penerbangan = 1.1016 Jarak = 4.3830 Tinggi = 1.5088
Waktu penerbangan = 1.0197 Jarak = 3.5265 Tinggi = 1.2912
Waktu penerbangan = 0.9068 Jarak = 2.5842 Tinggi = 1.0240
Waktu untuk masalah model: 0.454787



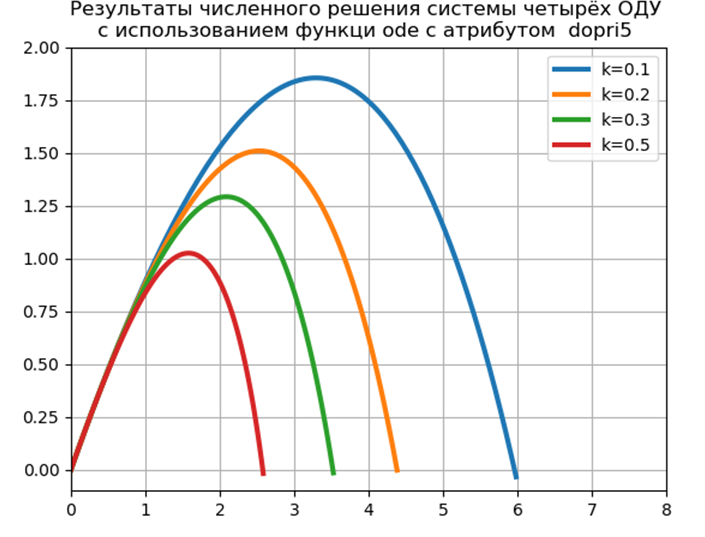
Untuk mengimplementasikan solusi numerik CDS menggunakan alat Python tanpa menggunakan modul khusus, saya mengusulkan dan menyelidiki fungsi berikut:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

Fungsi kenaikan (f, t, y, tau) menyediakan urutan kelima dari metode solusi numerik. Fitur lain dari program ini dapat ditemukan dalam daftar berikut:

Daftar program
 from numpy import* import matplotlib.pyplot as plt import time start = time.time() def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau):#     β€”β€”. k1=tau*f(t,y) k2=tau*f(t+(1/4)*tau,y+(1/4)*k1) k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2) k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3) k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4) k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5) return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6 t = []#   t y= []#   y t.append(to)#   t   to y.append(yo)#   y   yo while to < tEnd:#     t,y tau = min(tau, tEnd - to)#   tau yo = yo + increment(f, to, yo, tau) #     t0,y0    to = to + tau #   t.append(to) #   t y.append(yo) #   y return array(t), array(y) def f(t, y): #      f = zeros([4]) f[0]=y[1] f[1]=-k*y[1]*sqrt(y[1]**2+y[3]**2) f[2]=y[3] f[3]=-k*y[3]*sqrt(y[1]**2+y[3]**2) -g if y[3]<0 and y[2]<=0.0: #    return -1 return f to = 0#     tEnd = 1.41#     alph=pi/4#    v0=10.0 #   K=[0.1,0.2,0.3,0.5]#     g=9.81 yo = array([0.,v0*cos(alph),0.,v0*sin(alph)]) #   tau =0.01#  for i in K: #      k=i t, y = rungeKutta(f, to, yo, tEnd, tau) y1=array([i[0] for i in y]) #     y y3=array([i[2] for i in y]) #    ""     s,h,t plt.plot(y1,y3,linewidth=2,label='k=%.1f h=%.3f s=%.2f t=%s' % (k,max(y3),max(y1),round(t[list(y1).index(max(y1))],3))) stop = time.time() plt.title("      \n     Python\n  β€”β€” ") print ("   : %f"%(stop-start)) plt.xlabel(' h') plt.ylabel(' s') plt.legend(loc='best') plt.xlim(0,8) plt.ylim(-0.1,2) plt.grid(True) plt.show()


Kami mendapatkan:

Waktu untuk masalah model: 0.259927



Kesimpulan

Implementasi perangkat lunak yang diusulkan untuk masalah model tanpa menggunakan modul khusus memiliki kinerja hampir dua kali lebih cepat daripada dengan fungsi ode, tetapi kita tidak boleh lupa bahwa ode memiliki akurasi yang lebih tinggi dari solusi numerik dan kemungkinan memilih metode solusi.

Memecahkan masalah nilai batas dengan kondisi batas yang dipisahkan benang


Kami memberikan contoh masalah nilai batas tertentu dengan kondisi batas yang dipisahkan utas:

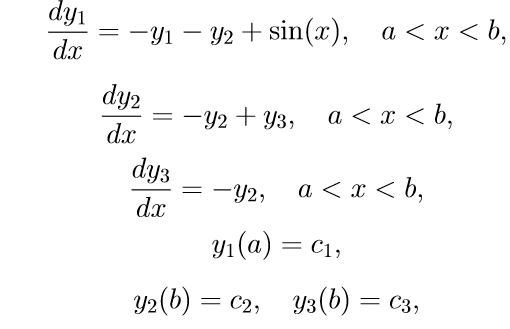
(11)

Untuk mengatasi masalah (11), kami menggunakan algoritma berikut:

1. Kami menyelesaikan tiga persamaan sistem homogen (11) yang pertama dengan kondisi awal

Kami memperkenalkan notasi untuk menyelesaikan masalah Cauchy:


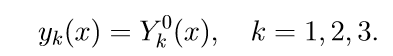
2. Kami menyelesaikan tiga persamaan homogen sistem pertama (11) dengan kondisi awal

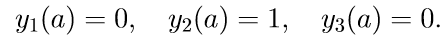
Kami memperkenalkan notasi untuk menyelesaikan masalah Cauchy:


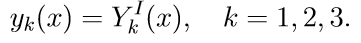
3. Kami menyelesaikan tiga persamaan homogen sistem pertama (11) dengan kondisi awal



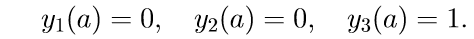
Kami memperkenalkan notasi untuk menyelesaikan masalah Cauchy:



4. Solusi umum masalah nilai batas (11) menggunakan solusi masalah Cauchy ditulis sebagai kombinasi linear dari solusi:

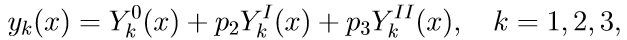
di mana p2, p3 adalah beberapa parameter yang tidak diketahui.

5. Untuk menentukan parameter p2, p3, kami menggunakan kondisi batas dari dua persamaan terakhir (11), yaitu kondisi untuk x = b. Mengganti, kita memperoleh sistem persamaan linear sehubungan dengan p2, p3 yang tidak diketahui:
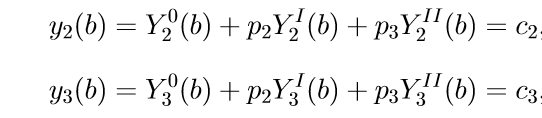
(12)
Memecahkan (12), kita memperoleh relasi untuk p2, p3.

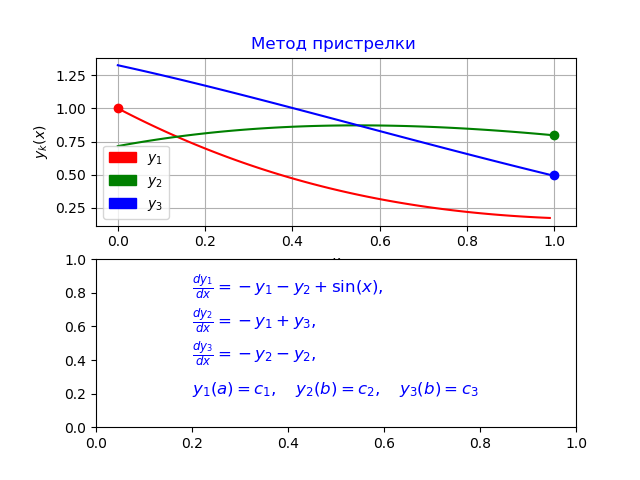
Menggunakan algoritma di atas menggunakan metode Runge - Kutta - Felberg, kami mendapatkan program berikut:

Daftar program
  #   from numpy import* import matplotlib.pyplot as plt import matplotlib.font_manager as fm,os import matplotlib.patches as mpatches import matplotlib.lines as mlines from scipy.integrate import odeint from scipy import linalg import time start = time.time() c1 = 1.0 c2 = 0.8 c3 = 0.5 a =0.0 b = 1.0 nn =100 initial_state_0 =array( [a, c1, 0.0, 0.0]) initial_state_I =array( [a, 0.0, 1.0, 0.0]) initial_state_II =array( [a, 0.0, 0.0, 1.0]) to = a tEnd =b N = int(nn) tau=(ba)/N def rungeKutta(f, to, yo, tEnd, tau): def increment(f, t, y, tau): k1=tau*f(t,y) k2=tau*f(t+(1/4)*tau,y+(1/4)*k1) k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2) k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3) k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4) k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5) return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6 t = [] y= [] t.append(to) y.append(yo) while to < tEnd: tau = min(tau, tEnd - to) yo = yo + increment(f, to, yo, tau) to = to + tau t.append(to) y.append(yo) return array(t), array(y) def f(t, y): global theta f = zeros([4]) f[0] = 1 f[1] = -y [1]-y[2] +theta* sin(y[0]) f[2] = -y[2]+y[3] f[3] = -y[2] return f #    -- theta = 1 theta = 1.0 yo =initial_state_0 t, y = rungeKutta(f, to, yo, tEnd, tau) y2=[i[2] for i in y] y3=[i[3] for i in y] #       # Y20 = Y2(b), Y30 = Y3(b) Y20 = y2[N-1] Y30 = y3[N-1] #    -- theta = 0,  I theta = 0.0 yo= initial_state_I t, y = rungeKutta(f, to, yo, tEnd, tau) y2=[i[2] for i in y] y3=[i[3] for i in y] #       # Y21= Y2(b), Y31 = Y3(b) Y21= y2[N-1] Y31 = y3[N-1] #    -- theta = 0,  II theta = 0.0 yo =initial_state_II t, y = rungeKutta(f, to, yo, tEnd, tau) y2=[i[2] for i in y] y3=[i[3] for i in y] #       # Y211= Y2(b), Y311 = Y3(b) Y211= y2[N-1] Y311 = y3[N-1] #    #     p2, p3 b1 = c2 - Y20 b2 = c3 - Y30 A = array([[Y21, Y211], [Y31, Y311]]) bb = array([[b1], [b2]]) #   p2, p3 = linalg.solve(A, bb) #    #  , theta = 1 theta = 1.0 yo = array([a, c1, p2, p3]) t, y = rungeKutta(f, to, yo, tEnd, tau) y0=[i[0] for i in y] y1=[i[1] for i in y] y2=[i[2] for i in y] y3=[i[3] for i in y] #  print('y0[0]=', y0[0]) print('y1[0]=', y1[0]) print('y2[0]=', y2[0]) print('y3[0]=', y3[0]) print('y0[N-1]=', y0[N-1]) print('y1[N-1]=', y1[N-1]) print('y2[N-1]=', y2[N-1]) print('y3[N-1]=', y3[N-1]) j = N xx = y0[:j] yy1 = y1[:j] yy2 = y2[:j] yy3 = y3[:j] stop = time.time() print ("   : %f"%(stop-start)) plt.subplot(2, 1, 1) plt.plot([a], [c1], 'ro') plt.plot([b], [c2], 'go') plt.plot([b], [c3], 'bo') plt.plot(xx, yy1, color='r') #  plt.plot(xx, yy2, color='g') #  plt.plot(xx, yy3, color='b') #  plt.xlabel(r'$x$') #   x   TeX plt.ylabel(r'$y_k(x)$') #   y   TeX plt.title(r'  ', color='blue') plt.grid(True) # patch_y1 = mpatches.Patch(color='red', label='$y_1$') patch_y2 = mpatches.Patch(color='green', label='$y_2$') patch_y3 = mpatches.Patch(color='blue', label='$y_3$') plt.legend(handles=[patch_y1, patch_y2, patch_y3]) ymin, ymax = plt.ylim() xmin, xmax = plt.xlim() plt.subplot(2, 1, 2) font = {'family': 'serif', 'color': 'blue', 'weight': 'normal', 'size': 12, } plt.text(0.2, 0.8, r'$\frac{dy_1}{dx}= - y_1 - y_2 + \sin(x),$', fontdict=font) plt.text(0.2, 0.6,r'$\frac{dy_2}{dx}= - y_1 + y_3,$', fontdict=font) plt.text(0.2, 0.4, r'$\frac{dy_3}{dx}= - y_2 - y_2,$', fontdict=font) plt.text(0.2, 0.2, r'$y_1(a)=c_1, ' r'\quad y_2(b)=c_2, \quad y_3(b)=c_3.$', fontdict=font) plt.subplots_adjust(left=0.15) plt.show()


Kami mendapatkan:

y0 [0] = 0,0
y1 [0] = 1.0
y2 [0] = 0.7156448588231397
y3 [0] = 1.324566562303714
y0 [N-1] = 0.9900000000000007
y1 [N-1] = 0.1747719838716767
y2 [N-1] = 0,8
y3 [N-1] = 0,5000000000000001
Waktu untuk masalah model: 0,070878



Kesimpulan



Program yang dikembangkan oleh saya berbeda dari kesalahan yang diberikan pada [3], yang mengkonfirmasi analisis komparatif dari fungsi odeint yang diberikan pada awal artikel dengan metode Runge - Kutta - Felberg diimplementasikan dalam Python.

Referensi:

1. Solusi numerik dari model matematika objek yang didefinisikan oleh sistem komposit persamaan diferensial.

2. Pengantar Python ilmiah.

3. N.M. Polyakova, E.V. Shiryaeva Python 3. Membuat antarmuka pengguna grafis (menggunakan contoh penyelesaian masalah nilai batas untuk persamaan diferensial biasa linear dengan metode pemotretan). Rostov-on-Don 2017.

Source: https://habr.com/ru/post/id418139/

More articles:


All Articles