🥄 🤷🏿 💞 Manipulasi "manual" 💆🏾 🧓🏿 ☄️

Suatu ketika, selama tahun kedua saya di universitas, saya diberi tugas: memasak sesuatu "semacam" untuk mengkonfirmasi peringkat tinggi "insinyur robotika masa depan." Pada catatan pathos ini, saya pergi ke kedalaman kesadaran untuk mencari ide. Setelah perjalanan singkat, muncul ide tentang perangkat, teori penciptaan yang ingin saya bagikan kepada publik.

Inti dari pengembangan adalah ini. Pertimbangkan manipulator 5 sumbu yang biasa (diagram struktural kinematik ditunjukkan pada gambar di bawah). Kemampuannya ketika bergerak di ruang angkasa luas: mampu membuat gerakan dalam 5 koordinat, dan pada saat yang sama, yaitu 3 koordinat sepanjang tiga sumbu XYZ dan rotasi di sekitar dua dari mereka. Dalam hal ini, elemen kerja dari manipulator mampu menempati posisi apa pun di ruang kerja dan pada saat yang sama mempertahankan orientasi yang diperlukan dari badan kerja (tidak termasuk rotasi elemen kerja di sekitar porosnya sendiri).

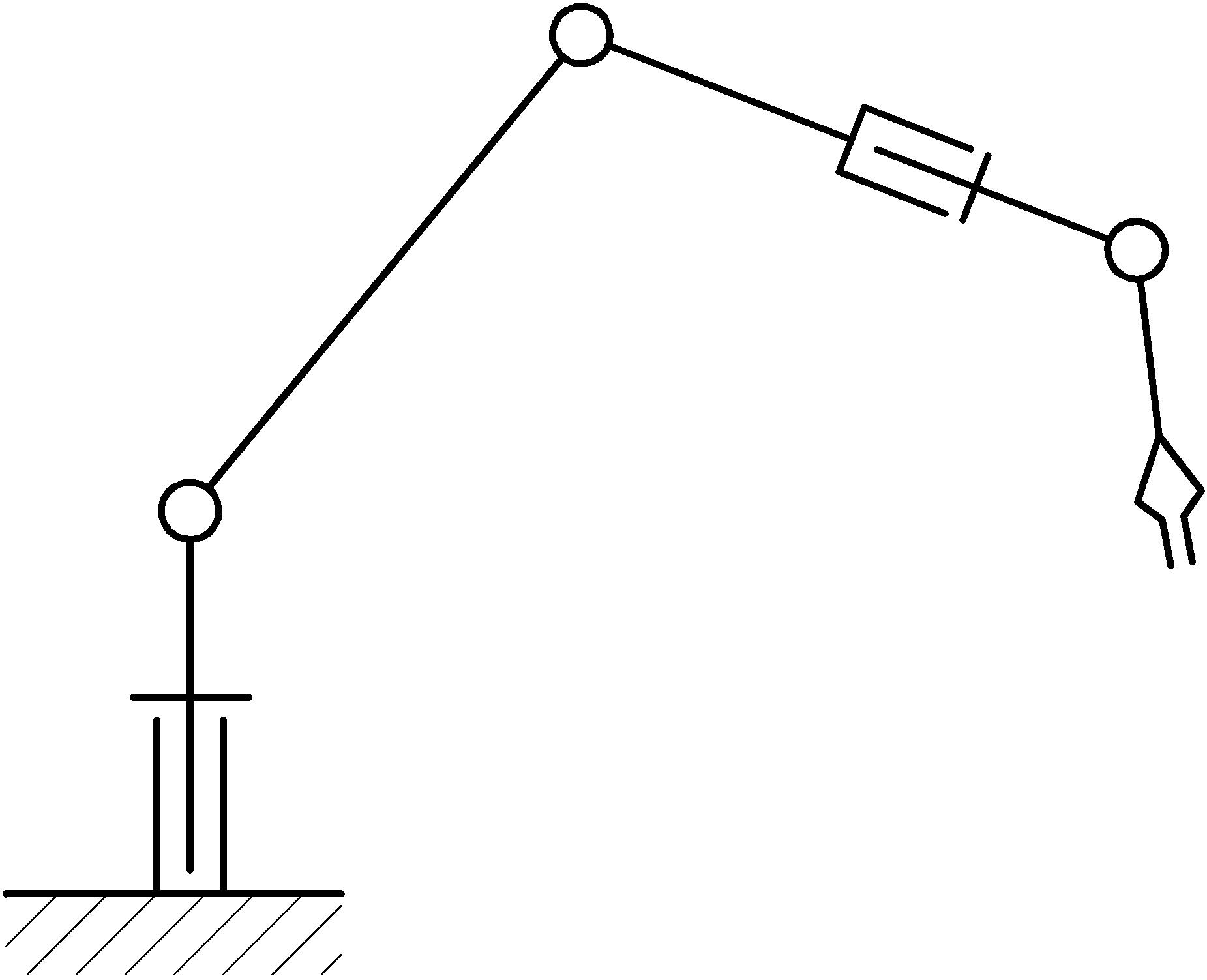
Desain ini berkaitan dengan manipulator dari tipe antropomorfik dan karena itu mampu, kira-kira tentu saja, mereproduksi gerakan tangan manusia. Berdebat tentang tesis ini, muncul ide bahwa akan menarik untuk membuat manipulator jarak jauh menyalin gerakan tangan saya secara real time. Jadi saya hanya meletakkan sensor di tangan saya yang membaca gerakan tangan (baik linier dan sudut), dan hal mekanis ini akan mengulanginya setelah saya. Karena manipulator dapat melakukan fungsi menggerakkan dan mengorientasikan tubuh yang bekerja, maka dengan bantuan tangan seseorang dapat menggerakkan dan mengorientasikan telapak tangannya, oleh karena itu kedua proses ini serupa dan dapat direpresentasikan sebagai satu proses yang sama - penangkapan gerakan tangan oleh manipulator secara real time.

Mengulurkan bibirnya

Ke depan, saya akan mengatakan bahwa itu hanya mungkin untuk mewujudkan penangkapan gerakan berorientasi telapak tangan, yaitu. Saya bisa mengendalikan orientasi tubuh yang bekerja, tetapi bukan gerakan linearnya di ruang angkasa.

Ini melengkapi pernyataan masalah. Sekarang mari kita menganalisis tugas (bahasa tidak berubah untuk menyebutnya sebagai "tugas teknis"). Penting untuk mengembangkan dua perangkat yang independen secara struktural: manipulator itu sendiri dan perangkat pelacakan gerakan, yang dipasang pada lengan. Ini akan diikuti oleh proses yang memakan waktu untuk membuat deskripsi matematis, menyusun algoritma dan menulis perangkat lunak. Kami membagi proyek menjadi tiga bagian:

1. Perkembangan manipulator
2. Pengembangan perangkat untuk melacak pergerakan lengan
3. Yang lainnya

Secara singkat tentang masing-masing tahapan:

Semuanya sepele di sini ... Dalam CAD, kami mendesain struktur, melakukan gambar bagian dan manufaktur, lalu berkumpul. Kemudian kami menghitung kinematika dan menulis perangkat lunak kami sendiri, yang akan menyembunyikan panggilan tingkat rendah ke drive.
Pada tahap ini, kami menentukan jenis sensor, mendesain diagram sirkuit, membuat papan sirkuit cetak, mengembangkan algoritma untuk menentukan posisi di ruang angkasa, menulis perangkat lunak.
Sebenarnya, untuk tahap-tahap sebelumnya - membuat manipulator mematuhi pemiliknya. Di sini saya mengembangkan algoritma untuk mengubah koordinat ke dalam bidang kerja manipulator.

1. Perkembangan manipulator

Dalam proyek ini, seperti yang disebutkan di atas, kami menggunakan manipulator dengan 5 derajat kebebasan. Sejumlah derajat kebebasan seperti itu sudah cukup, karena mereka termasuk tiga perpindahan linear dan dua rotasi. Dua yang terakhir diperlukan untuk orientasi benda kerja, karena arah PO di ruang dapat ditentukan dalam bentuk vektor, dan vektor pasti dapat dipulihkan dari dua sudut rotasi (tidak memperhitungkan panjangnya). Dalam hal ini, kita membutuhkan lima koordinat umum, sama dengan jumlah sumbu.

Tautan manipulator dihubungkan oleh pasangan kinematik rotasi kelas lima. Desain manipulator adalah standar untuk tipenya (skema kinematik disajikan pada awal artikel). Ini memiliki tempat tidur tetap, dengan mana sistem koordinat dasar terhubung, dudukan putar, di mana tautan bergerak yang tersisa terpasang, terhubung dalam rantai. Badan yang bekerja melekat pada tautan akhir (mengarah), dalam hal ini tiruannya dalam bentuk penunjuk berbentuk panah (lihat gambar di bawah).

Laporan foto perakitan

Model 3D dibangun dalam CAD "Kompas 3D". Bagian bahan - kayu lapis 4 mm dan PLA untuk bagian plastik. Bagian-bagian dari kayu lapis dipotong pada mesin laser, bagian-bagian dari plastik dicetak pada printer 3D. Servo digital Dynamixel AX-12 digunakan sebagai drive sumbu. Munculnya manipulator menyerupai satu serangga keji, dari mana ia menerima julukan "Komar".

Deskripsi matematis kinematika

Pada tahap ini, perlu untuk menghitung kinematika langsung dan terbalik dari manipulator. Tugas langsung adalah menentukan posisi tautan relatif terhadap beberapa sistem koordinat dasar menggunakan nilai yang diketahui dari koordinat umum (dalam hal ini, sudut rotasi tautan). Tugas terbalik yang disebut kinematika terbalik atau terbalik, terdiri dalam menentukan parameter koordinat umum untuk mencapai posisi dan orientasi yang diinginkan dari badan kerja manipulator.

Mari kita mulai dengan menghitung kinematika terbalik. Mari kita gambarkan skema geometrik manipulator, dari mana hubungan geometris yang menarik bagi kita akan menjadi jelas.

Posisi yang diperlukan diwakili oleh vektor radius

v e c r

$\ vec {r}$ . Perlu dijelaskan mengapa vektor

v e c r

$\ vec {r}$ ditarik ke titik mengarah, dan bukan ke titik akhir RO. Karena orientasi badan kerja diketahui oleh kita sebelumnya (saya sendiri menentukannya sesuai dengan beberapa persyaratan), perlu bahwa titik mengarah berada di tempat yang tepat, ditunjukkan sebagai vektor

v e c r

$\ vec {r}$ . Vektor ini diperoleh dengan mengurangi dari vektor radius

v e c R

$\ vec {R}$ ditarik ke titik akhir PO, vektor orientasinya

v e c v_{0}

$\ vec {v_0}$ , relatif terhadap BSK, yaitu .:

v e c r = v e c R - v e c v_{0}

$\ vec {r} = \ vec {R} - \ vec {v_0}$

Pertimbangkan transisi titik mengarah ke posisi yang diinginkan. Hal ini dilakukan oleh rotasi tautan a dan b (saya menggambarkannya dalam bentuk vektor) di engsel A , B dan C. Asal usul sistem koordinat basis (BSC) ditempatkan pada titik engsel B. Sumbu rotasi engsel A diarahkan sepanjang sumbu Z , sumbu B dan C diarahkan tegak lurus ke Z.

Ketika semua formalitas terpenuhi, mari kita langsung ke intinya. Untuk mengatasi masalah kinematika terbalik, saya menggunakan pendekatan geometris karena kesederhanaan desain manipulator. Dari geometri dapat dilihat bahwa vektor

v e c r

$\ vec {r}$ sama dengan jumlah vektor tautan

v e c a

$\ vec {a}$ dan

v e c b

$\ vec {b}$ . Sudut

t h e t a

$\ theta$ ,

g a m m a_{1}

$\ gamma_1$ ,

g a m m a_{2}

$\ gamma_2$ - sudut rotasi masing-masing link A , B dan C.
Pertimbangkan segitiga yang dibatasi oleh vektor

v e c r

$\ vec {r}$ ,

v e c a

$\ vec {a}$ dan

v e c b

$\ vec {b}$ . Dari segitiga ini, dengan teorema kosinus, kita menemukan sudut

a l p h a

$\ alpha$ dan

b e t a

$\ beta$ . Biarkan panjang vektor sama dengan:

| v e c r | = r q u a d | v e c a | = a q u a d | v e c b | = b

$| \ vec {r} | = r \ quad | \ vec {a} | = a \ quad | \ vec {b} | = b$

Kami menulis teorema kosinus mengenai sudut yang diinginkan:

b^{2} = a^{2} + r^{2} - 2 a r c o s (a l p h a) r^{2} = a^{2} + b^{2} - 2 a b c o s (b e t a)

$b ^ 2 = a ^ 2 + r ^ 2-2ar \ cos (\ alpha) \\ r ^ 2 = a ^ 2 + b ^ 2-2ab \ cos (\ beta)$

Ekspresikan sudutnya

a l p h a

$\ alpha$ dan

b e t a

$\ beta$ :

a l p h a = a r c c o s k i r i (f r a c a^{2} + r^{2} - b^{2} 2 a r k a n a n) q u a d b e t a = a r c c o s k i r i (f r a c a^{2} + b^{2} - r^{2} 2 a b k a n a n)

$\ alpha = \ arccos \ kiri (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ar} \ kanan) \ quad \ beta = \ arccos \ kiri (\ frac {a ^ 2 + b ^ 2 -r ^ 2} {2ab} \ kanan)$

Dapat dilihat dari diagram geometrik bahwa:

t h e t a = a r c t a n = k i r i (f r a c r_{y} r_{x} k a n a n) q u a d o m e g a = a r c s i n = k i r i (f r a c r_{z} r k a n a n)

$\ theta = \ arctan = \ kiri (\ frac {r_y} {r_x} \ kanan) \ quad \ omega = \ arcsin = \ kiri (\ frac {r_z} {r} \ kanan)$

Lalu:

g a m m a_{1} = o m e g a + a l p h a q u a d g a m m a_{2} = 180^{} c i r c - b e t a

$\ gamma_1 = \ omega + \ alpha \ quad \ gamma_2 = 180 ^ \ circ- \ beta$

Akhirnya, transisi dari koordinat linier ke sudut rotasi tautan dilakukan oleh rumus:

t h e t a = a r c t a n k i r i (f r a c r_{y} r_{x} k a n a n) g a m m a_{1} = a r c s i n k i r i (f r a c r_{z} r k a n a n) + a r c c o s k i r i (f r a c a^{2} + r^{2} - b^{2} 2 a b k a n a n) g a m m a_{2} = 180^{} c i r c - a r c c o s k i r i (f r a c a^{2} + b^{2} - r^{2} 2 a r k a n a n)

$\ theta = arctan \ kiri (\ frac {r_y} {r_x} \ kanan) \\ \ gamma_1 = arcsin \ kiri (\ frac {r_z} {r} \ kanan) + arccos \ kiri (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ab} \ kanan) \\ \ gamma_2 = 180 ^ \ circ-arccos \ kiri (\ frac {a ^ 2 + b ^ 2-r ^ 2} {2ar} \ kanan)$

Sekarang setelah Anda memindahkan titik mengarah ke posisi yang diinginkan, Anda harus mengarahkan badan kerja dengan benar. Untuk melakukan ini, Anda perlu mengetahui koordinat vektor

v e c v

$\ vec {v}$ relatif terhadap titik mengarah, yaitu koordinat berdasarkan sistem koordinat lokal (LSC) -

E^{'}

${E '}$ , awal yang terletak di titik mengarah manipulator.

E^{'} = k i r i [v e c x^{'} v e c y^{'} v e c z^{'} k a n a n]

$E '= \ kiri [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ kanan]$

Vektor

v e c x^{'}

$\ vec {x} '$ diarahkan oleh tautan b , vektor

v e c y^{'}

$\ vec {y} '$ - di sepanjang sumbu putar f1 .
Untuk menemukan dasar

E

$E$ kami mendefinisikan matriks transisi dari BSK (dengan basis

E_{0}

$E_0$ ) dan LSK. Matriks ini diperoleh dengan kombinasi rotasi di engsel A , B dan C :

E^{'} = C E_{0}

$E '= CE_0$

dimana

C = R_{C} R_{B} R_{A}

$C = R_CR_BR_A$

Karena matriks

E_{0}

$E_0$ lajang, maka:

E^{'} = C = R_{C} R_{B} R_{A}

$E '= C = R_CR_BR_A$

Pembaca yang berpengetahuan luas

Pembaca berpengetahuan dapat menemukan kesamaan di sini dengan presentasi Denavit-Hartenberg untuk memecahkan masalah kinematika langsung. Ya, ini dia, disederhanakan menjadi tidak mungkin dan dengan perubahan kecil saya. Di sini saya tidak menggunakan transformasi homogen, tidak memperhitungkan fitur desain akun, seperti perpindahan sudut dan linear sumbu, dll. Hanya saja saya mendesain desain sehingga tidak ada parameter tambahan yang disebutkan di atas, hanya menyisakan koordinat yang digeneralisasi.

Matriks

C

$C$ itu dihitung dengan mengalikan matriks rotasi di sekitar sumbu dengan sudut .
Kami mendefinisikan fungsi yang menghitung matriks ini:

f = a x i s A n g l e 2 r o t M a t (s u m b u, s u d u t)

$f = axisAngle2rotMat (sumbu, sudut)$

Sumbu diambil dalam bentuk vektor sebagai kolom matriks yang diperoleh oleh rotasi sebelumnya, dan sudut sudah dihitung di atas.

C_{A} = a x i s A n g l e 2 r o t M a t (E_{0}^{l a n g l e 3 r a n g l e}, t h e t a) C_{B A} = R_{B} C_{A} = a x i s A n g l e 2 r o t M a t (C_{A}^{l a n g l e 2 r a n g l e}, g a m m a_{1}) C_{A} C_{C B A} = R_{C} C_{B A} = a x i s A n g l e 2 r o t M a t (C_{B A}^{l a n g l e 2 r a n g l e}, g a m m a_{1}) C_{B A}

$C_A = axisAngle2rotMat (E_0 ^ {\ langle3 \ rangle}, \ theta) \\ C_ {BA} = R_BC_A = axisAngle2rotMat (C_A ^ {\ langle2 \ rangle}, \ gamma_1) C_A \\ C_ {CBA} = R_CC_ { BA} = axisAngle2rotMat (C_ {BA} ^ {\ langle2 \ rangle}, \ gamma_1) C_ {BA}$

Sebagai hasilnya, kita mendapatkan:

C = C_{C B A} q u a d E^{'} = C

$C = C_ {CBA} \ quad E '= C$

Biarkan vektor badan kerja di BSK

v e c v_{0}

$\ vec {v_0}$ . Maka kesetaraan itu benar:

v e c v_{0} = E^{'} v e c v

$\ vec {v_0} = E '\ vec {v}$

Dari sini kami ungkapkan

v e c v

$\ vec {v}$ - vektor dari badan yang bekerja di dasar

E

$E$ , yaitu relatif terhadap titik mengarah:

v e c v = E^{' T} v e c v_{0}

$\ vec {v} = E '^ T \ vec {v_0}$

Sekarang, dengan mengetahui vektor PO, kita dapat menghitung sudut rotasi sumbu orientasi f1 dan f2

Untuk memindahkan PO ke posisi tertentu, Anda perlu melakukan rotasi di sudut-sudutnya

v a r p h i_{1}

$\ varphi_1$ dan

v a r p h i_{2}

$\ varphi_2$ . Angka tersebut menunjukkan hal itu

v a r p h i_{1} = a r c t a n k i r i (f r a c v_{y} v_{z} k a n a n) q u a d v a r p h i_{2} = a r c s i n k i r i (f r a c s q r t v_{y}^{2} + v_{z}^{2} V k a n a n)

$\ varphi_1 = arctan \ kiri (\ frac {v_y} {v_z} \ kanan) \ quad \ varphi_2 = arcsin \ kiri (\ frac {\ sqrt {v_y ^ 2 + v_z ^ 2}} {V} \ kanan)$

dimana

V = | v e c v | = s q r t v_{x}^{2} + v_{y}^{2} + v_{z}^{2}

$V = | \ vec {v} | = \ sqrt {v_x ^ 2 + v_y ^ 2 + v_z ^ 2}$ - panjang tubuh yang bekerja,

v_{x}, v_{y}, v_{z}

$v_x, v_y, v_z$ - koordinat vektor

v e c v

$\ vec {v}$ .

Perangkat lunak manipulator dibagi menjadi dua level, atas dan bawah. Tingkat atas ditulis dalam Matlab dalam bentuk perpustakaan dan berbagai metode perintah, semakin rendah - pada mikrokontroler Atmega328. Tugas tingkat atas adalah merumuskan perintah yang dikirim ke mikrokontroler. Tugasnya adalah mendapatkan tim dan, sesuai dengan itu, pasang drive di posisi yang tepat. Dalam bentuk ini, sistem kontrol ternyata dapat diandalkan (sejauh ini ...) dan nyaman digunakan.

Mengapa matlab

Puncaknya, bagi saya, dari bahasa Matlab adalah bahwa operasi dengan matriks terjadi di sana seperti hubungan aljabar biasa, dan tidak perlu melampirkan loop bersarang, seperti yang dilakukan, misalnya, dalam C. Plus, hampir semua operasi matematika "diinginkan" tersedia di Matlab, yang memberi kebahagiaan luar biasa.

Perumusan perintah dan pengiriman dari tingkat atas adalah sebagai berikut: pengguna di jendela perintah Matlab memanggil fungsi dari perpustakaan (misalnya, fungsi hanya bergerak ke titik), menunjukkan argumen yang diperlukan (biasanya ini adalah koordinat dan orientasi PO). Setelah pertimbangan matematis yang dijelaskan di atas, direkam di perpustakaan, sudut rotasi sumbu dan, jika perlu, kecepatan rotasi dihitung. Setelah protokol sederhana, kami merakit perintah dan mengirimkannya ke mikrokontroler level bawah melalui port COM serial.

Beberapa kata tentang perpustakaan tertulis. Ini memiliki fungsi sebagai berikut:

fungsi koneksi serial
fungsi bergerak

ke titik, dengan kecepatan konstan semua drive
ke suatu titik, dengan pemberhentian terakhir dari semua drive (kecepatan drive dipilih secara proporsional dengan sudut rotasinya sendiri dan terbesar. Dengan demikian, pada akhir pendekatan ke titik, semua drive berhenti bergerak)
ke suatu titik, dengan gerakan halus setiap drive (dalam hal ini, grafik kecepatan terlihat seperti trapesium dengan area akselerasi, kecepatan konstan, dan pengereman)

Grafik
ke suatu titik, sesuai dengan sudut rotasi yang ditentukan secara manual dan kecepatan rotasi

Daftar fungsi tentu saja dapat diperluas, tetapi fungsi ini cukup untuk menyelesaikan secara langsung masalah yang dirancang manipulator.

Video menunjukkan operasi manipulator.

2. Pengembangan perangkat untuk melacak pergerakan lengan

Lanjutkan ke langkah berikutnya. Di sini Anda perlu merancang perangkat khusus yang dapat melacak secara real time posisi di telapak tangan Anda. Juga, proses ini disebut "motion capture". Untuk mengimplementasikan rencana tersebut, saya memutuskan untuk menggunakan sistem navigasi inersia strapdown (SINS) berdasarkan tiga sensor: giroskop, akselerometer, dan magnetometer. Sekelompok sensor ini disebut IMU - sensor (dalam terjemahan, ini adalah SINS yang sama).

Pertama, saya merancang papan sirkuit tercetak dengan fungsi yang saya butuhkan, di mana saya menempatkan ketiga sensor ini. Sebagai pengontrol pemrosesan, saya memilih (atau lebih tepatnya mengambil apa) mikrokontroler Atmega2560. Sensor yang digunakan umum dan murah di pasar Cina. Ini adalah sensor berpasangan giroskop tiga sumbu dan akselerometer MPU6050 dan magnetometer HMC5883l.

Foto papan yang sudah jadi

Algoritma untuk menghitung posisi dalam ruang cukup sederhana: pertama, kami menentukan orientasi dalam bentuk dasar sistem koordinat lokal (LSC), yang terhubung dengan sensor, dan akhirnya dengan telapak tangan.

Orientasi ditentukan relatif terhadap sistem koordinat awal (NSC), yang pada dasarnya adalah posisi awal perangkat pada saat power-up. Basis NSC dan LSC terdiri dari vektor-vektor kolom dari ort-nya:

E_0 = \ kiri [\ vec {X} \ \ vec {Y} \ \ vec {Z} \ kanan] = \ kiri [\ mulai {array} {cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \ end {array} \ kanan] \\ E '= \ kiri [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ kanan]

$E_0 = \ kiri [\ vec {X} \ \ vec {Y} \ \ vec {Z} \ kanan] = \ kiri [\ mulai {array} {cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \ end {array} \ kanan] \\ E '= \ kiri [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ kanan]$

Mereka terkait dengan rasio:

E^{'} = C E_{0}

$E '= CE_0$

Dimana

C

$C$ Merupakan matriks transisi, juga merupakan matriks rotasi dalam ruang. Kami menganggap dasar NSC sebagai matriks identitas. Oleh karena itu

E^{'} = C

$E '= C$

.
Setelah itu, vektor akselerasi

v e c A

$\ vec {A}$ , yang diketahui sehubungan dengan LSC, harus ditentukan dalam NSC. Ini dilakukan dengan mengalikan vektor kolom akselerasi dengan basis LSC:

v e c A = E^{'} v e c A^{'}

$\ vec {A} = E '\ vec {A}'$

Kemudian kami mengintegrasikan vektor percepatan yang diperoleh dua kali dari waktu ke waktu dan memperoleh jarak, mis. koordinat:

v e c r = i i n t v e c A d t

$\ vec {r} = \ iint \ vec {A} dt$

Upaya pertama untuk mengimplementasikan algoritma ini sangat naif ... Naifnya adalah saya menganggap itu mungkin hanya dari giroskop, menggunakan integrasi diskrit, untuk mendapatkan matriks rotasi di sekitar sumbu. Sumbu dalam hal ini dapat dianggap sebagai pseudovektor kecepatan sudut, yang komponennya (proyeksi pada sumbu) adalah output dari sensor gyro. Dan sudut, pada gilirannya, diperoleh dengan mengintegrasikan modul vektor. Antusiasme dan antusiasme awal menghilang ketika saya melihat ukuran yang mengerikan, yang disebut "zero drift", disebabkan oleh kesalahan akumulasi karena kesalahan integrasi diskrit dan kebisingan intrinsik dari sensor. Bahkan kemudian, saya mempunyai pemikiran bahwa menurut accelerometer, yang menunjukkan vektor, kebalikan dari vektor percepatan gravitasi (selanjutnya disebut sebagai vektor gravitasi), Anda dapat membuat koreksi matriks, tetapi di sini ada ketidakpastian terkait dengan fakta bahwa koreksi dimungkinkan. hanya hingga rotasi sudut di sekitar sumbu Z. Koreksi akan selesai jika dimungkinkan untuk mengembalikan matriks rotasi dengan cara alternatif, mis. tanpa menggunakan data gyro.

Sangat tertarik

Khusus tertarik saya akan jelaskan. Mengapa tidak mungkin mengembalikan matriks rotasi dengan accelerometer? Lebih tepatnya, tidak cukup data. Seperti yang kita ketahui, vektor gravitasi selalu diarahkan ke pusat planet, dan, oleh karena itu, tegak lurus ke permukaan bumi. Karena kita menghubungkan sistem koordinat awal, misalnya, dengan meja, sehingga bidang XY sejajar dengan permukaan meja, yang pada gilirannya paralel (dengan beberapa konvensi) ke lantai, dan lantai pada gilirannya sejajar dengan bidang dasar bangunan, yang biasanya merupakan bidang garis singgung ke Bumi. . Dari sini kami menyimpulkan bahwa pembacaan accelerometer saat istirahat (atau dengan gerakan seragam) memberi tahu kami tentang posisi sumbu

v e c z^{'}

$\ vec {z} '$ LSK, relatif terhadap NSC. Tentang ini, kegunaan data ini habis, karena rotasi di sekitar sumbu

v e c z^{'}

$\ vec {z} '$ jangan mengubah poros itu sendiri

v e c z^{'}

$\ vec {z} '$ tetapi mengubah dua sumbu lainnya

v e c x^{'}

$\ vec {x} '$ dan

v e c y^{'}

$\ vec {y} '$ . Karena itu, pembacaan accelerometer tidak akan berubah dan kemudian posisinya tidak akan ditentukan.

Maka perlu untuk menggunakan faktor lain yang memungkinkan untuk membuat penyesuaian penuh situasi. Faktor ini adalah medan magnet Bumi, yang, bersama dengan gravitasi pada satu titik di planet ini, tidak berubah seiring waktu (tentu saja dalam jangka pendek). Ini diukur menggunakan sensor HMC5883l tersebut di atas. Dalam hal ini, kami memiliki dua vektor, yang cukup untuk menentukan posisi di ruang relatif terhadap mereka.

Sekarang muncul pertanyaan logis - "bagaimana melakukan ini?" Setelah upaya yang gagal untuk menjawab pertanyaan ini, saya memanjat Internet sendiri, di mana saya menemukan informasi yang saya butuhkan. Tugas menentukan orientasi dalam ruang menurut tiga pengukuran (kecepatan sudut, vektor gravitasi dan vektor medan magnet) juga muncul dalam desain pesawat amatir (misalnya, helikopter), sehingga masalah ini telah berulang kali dipecahkan dengan berbagai metode. Salah satu metode yang populer adalah filter Majwick (Sebastian OH Madgwick). Setelah membaca artikel asli dan tidak mengerti bahasa Inggris, saya beralih ke terjemahan yang bagus (terima kasih kepada penulis untuk pekerjaan yang dilakukan). Sambil mempelajari studi artikel, saya semakin sering memiliki ide untuk mencoba menulis algoritma filter penentuan posisi saya sendiri, mengingat pada saat ini tingkat pengetahuan saya di bidang ini telah meningkat secara signifikan. Demi menarik, “ciptakan sepeda”! Dan saya "menciptakan" itu. Di bawah ini saya berikan alasan.

Algoritma menggunakan pembacaan ketiga sensor. Biarkan saya mengingatkan Anda bahwa tugas algoritma adalah untuk menghitung orientasi objek dan mengkompensasi nol penyimpangan giroskop, mengingat pasangan accelerometer dan magnetometer yang diberikan. Sebagai alat matematika yang menggambarkan posisi, angka empat digunakan, karena itu nyaman dalam hal membangun dan mengoptimalkan algoritma dan membutuhkan lebih sedikit operasi matematika untuk menghitungnya, tidak seperti matriks. Angka empat rotasi dalam ruang adalah sebagai berikut:

q = k i r i [q_{1} q_{2} q_{3} q_{4} k a n a n]

$q = \ kiri [q_1 \ q_2 \ q_3 \ q_4 \ kanan]$

Mengetahui sumbu rotasi yang dijelaskan oleh vektor yang dinormalisasi

v e c v = k i r i [v_{x} v_{y} v_{z} k a n a n]

$\ vec {v} = \ kiri [v_x \ v_y \ v_z \ kanan]$ dan sudut

v a r p h i

$\ varphi$ (dari mana asalnya) Anda dapat menghitung angka empat:

q_{v, v a r p h i} = k i r i [c o s k i r i (f r a c v a r p h i 2 k a n a n) v_{x} s i n k i r i (f r a c v a r p h i 2 k a n a n) v_{y} s i n k i r i (f r a c v a r p h i 2 k a n a n) v_{z} s i n k i r i (f r a c v a r p h i 2 k a n a n) k a n a n] q u a d (*)

$q_ {v, \ varphi} = \ kiri [\ cos \ kiri (\ frac {\ varphi} {2} \ kanan) \ \ v_x \ sin \ kiri (\ frac {\ varphi} {2} \ kanan) \ \ v_y \ sin \ kiri (\ frac {\ varphi} {2} \ kanan) \ \ v_z \ sin \ kiri (\ frac {\ varphi} {2} \ kanan) \ kanan] \ quad (*)$

Kemudian, hanya menggunakan giroskop, pada setiap iterasi siklus kita akan menghitung nilai saat ini dari angka empat sesuai dengan ungkapan:

q_{n}^{G} = q_{n - 1} q_{v, d v a r p h i}

$q_n ^ G = q_ {n-1} q_ {v, d \ varphi}$

Di sini

q_{n}^{G}

$q_n ^ G$ - angka empat pada waktu tertentu. Indeks G di atas menunjukkan bahwa nilai ini mengacu pada pengukuran relatif terhadap bacaan gyro, yaitu. kecepatan sudut;

q_{n - 1}

$q_ {n-1}$ - nilai angka empat pada saat sebelumnya dalam waktu;

q_{v, d v a r p h i}

$q_ {v, d \ varphi}$ –Mengubah posisi dalam satu langkah pengukuran, kita dapat mengatakan perubahan posisi secara terpisah oleh suatu sudut

d v a r p h i

$d \ varphi$ untuk

d t

$dt$ Apakah periode pengambilan sampel dinyatakan oleh angka empat rotasi (*).

Langkah selanjutnya dalam perhitungan adalah menemukan matriks rotasi berdasarkan data dari sepasang sensor accelerometer dan magnetometer. Secara khusus, kami menganggap vektor gravitasi dan vektor induksi medan magnet Bumi, yang, sebagaimana disebutkan di atas, bersifat statis sehubungan dengan Bumi dan NSC terkait. Di sini tesisnya adalah ini: mengetahui nilai-nilai gravitasi dan induksi dalam basis LSC dan NSC, kita dapat menghitung matriks transisi (rotasi) dari NSC ke LSC dan angka empat rotasi dalam ruang .

Ditunjukkan oleh

v e c G

$\ vec {G}$ vektor gravitasi awal dinormalisasi. Dapat diambil sebagai berikut:

v e c G = {k i r i [0 0 1 k a n a n]}^{T}

$\ vec {G} = {\ kiri [0 \ 0 \ 1 \ kanan]} ^ T$

Melalui

v e c H

$\ vec {H}$ menunjukkan vektor induksi magnetik awal normal:

v e c H = {k i r i [H_{x} H_{y} H_{z} k a n a n]}^{T}

$\ vec {H} = {\ kiri [H_x \ H_y \ H_z \ kanan]} ^ T$

Vektor ketiga juga diperlukan.

v e c K

$\ vec {K}$ yang terkait dengan keduanya. Ini diperoleh dengan perkalian vektor

v e c H

$\ vec {H}$ pada

v e c G

$\ vec {G}$ :

v e c K = {k i r i [K_{x} K_{y} K_{z} k a n a n]}^{T} = v e c H k a l i v e c G = {k i r i [H_{y} - H_{x} 0 k a n a n]}^{T}

$\ vec {K} = {\ kiri [K_x \ K_y \ K_z \ kanan]} ^ T = \ vec {H} \ kali \ vec {G} = {\ kiri [H_y \ -H_x \ 0 \ kanan]} ^ T$

Sekarang matriks terbentuk

M_{0}

$M_0$ yang mencirikan posisi awal, mis. NSC, sejak pada awalnya, LSC bertepatan dengan NSC. Matriks diperoleh dari komponen vektor

v e c H

$\ vec {H}$ ,

v e c G

$\ vec {G}$ dan

v e c K

$\ vec {K}$ :

M_0 = \ kiri [\ vec {H} \ \ vec {G} \ \ vec {K} \ kanan] = \ kiri [\ mulai {array} {cccc} H_x & 0 & H_y \\ H_y & 0 & -H_x \\ H_z & 1 & 0 \ end { array} \ kanan]

$M_0 = \ kiri [\ vec {H} \ \ vec {G} \ \ vec {K} \ kanan] = \ kiri [\ mulai {array} {cccc} H_x & 0 & H_y \\ H_y & 0 & -H_x \\ H_z & 1 & 0 \ end { array} \ kanan]$

Demikian pula, tetapi sudah pada setiap iterasi loop, matriks yang sama dibuat

M^{'} = k i r i [v e c h v e c g v e c k k a n a n]

$M '= \ kiri [\ vec {h} \ \ vec {g} \ \ vec {k} \ kanan]$ dimana

v e c h

$\ vec {h}$ Apakah vektor induksi magnetik dinormalisasi saat ini,

v e c g

$\ vec {g}$ Apakah vektor gravitasi dinormalisasi saat ini,

v e c k = v e c h k a l i v e c g

$\ vec {k} = \ vec {h} \ kali \ vec {g}$ . Matriks ini mencirikan posisi LSC, karena vektor-vektor ini dikenal dalam sistem koordinat sensor, yang bertepatan dengan LSC. Kemudian, mengetahui kedua matriks, kita dapat menulis persamaan berikut:

E^{'} M^{'} = E_{0} M_{0}

$E'M '= E_0M_0$

Ini menghubungkan dua matriks yang ditemukan dalam keadaan yang berbeda. Diberi ekspresi

E^{'} = C E_{0}

$E '= CE_0$ dan dasar apa

E_{0}

$E_0$ Apakah matriks identitas, kita dapatkan:

C M^{'} = M_{0}

$CM '= M_0$

Dari sini kami mengungkapkan matriks transisi

C

$C$ :

C = {k i r i (M_{0}^{- 1} k a n a n)}^{T} M^{' T}

$C = {\ kiri (M_0 ^ {- 1} \ kanan)} ^ TM '^ T$

Faktor pertama, seperti yang dapat Anda pahami, dihitung hanya sekali pada awal algoritma, dan tidak memerlukan penghitungan ulang dalam proses. Faktor kedua terbentuk cukup mudah dan tidak secara paksa pada setiap iterasi siklus.

Setelah, ketika matriks transisi ditemukan, kami mengubahnya menjadi angka empat

q_{n}^{A}

$q_n ^ A$ (Algoritma untuk mengkonversi dari matriks ke angka empat adalah hal publik dan saya tidak akan memberikannya di sini).

Sebagai hasilnya, kita tahu dua angka empat ditemukan secara independen satu sama lain. Dan untuk menggabungkan hasilnya, saya menerapkan filter komplementer sederhana dengan koefisien

F

$F$ , yang diambil dari rentang 0 hingga 1:

q_{n} = F q_{n}^{G} + k i r i (1 - F k a n a n) q_{n}^{A}

$q_n = Fq_n ^ G + \ kiri (1-F \ kanan) q_n ^ A$

Sebagai hasilnya, kami mendapatkan angka empat, yang berisi informasi terkini tentang posisi di ruang perangkat dengan modul SINS.

Sepeda pergi ... Algoritma bekerja, tetapi dalam beberapa situasi berperilaku agak tidak tepat, yang pada prinsipnya tidak mengganggu, tetapi tidak memberikan alasan untuk berpikir positif tentang hal itu. Saya memuaskan minat olahraga saya, dan sekarang Anda dapat beralih ke solusi yang sudah jadi, lebih baik. Kemudian saya kembali ke artikel oleh Sebastian Majwik dan memutuskan untuk menggunakan algoritmanya, untungnya, orang yang luar biasa ini menerbitkan semua kode sumber di situs web proyek . Arsip memiliki kode sumber dalam berbagai bahasa, termasuk bahasa Matlab. Fakta ini mempengaruhi keputusan saya untuk meninggalkan ide melakukan semua perhitungan pada mikrokontroler (terutama karena itu 8-bit) dan menulis program yang sudah ada di komputer di lingkungan Matlab. Mikrokontroler hanya digunakan untuk menginterogasi sensor dan mengirim data ke PC (situasi yang sama dengan manipulator). Dalam hal ini, kode program utama yang mengalami perubahan dan debugging didasarkan pada lingkungan Matlab, yang sangat nyaman dalam prosesnya.

Nah, orientasi yang diberikan oleh angka empat kita dapatkan. Apa yang selanjutnya menurut rencana? Dan kemudian mengikuti koordinat linier objek sesuai dengan accelerometer. Nah, ini dia lebih baik untuk hanya menyatakan bahwa tidak mungkin untuk menentukan koordinat menggunakan accelerometer dengan akurasi yang diperlukan. Bahkan paling tidak menemukan perubahan posisi yang memadai! Tentu saja, ada upaya untuk menyelesaikan masalah ini, tetapi dalam waktu nyata tidak mungkin menemukan koordinat. Mengapa Karena integrasi diskrit ganda dari pembacaan sensor berisik hanya menyebabkan penerbangan ke stratosfer, dan pada kecepatan panik, tetapi tidak ke hasil yang positif. Oleh karena itu, saya memotong algoritme yang ditunjukkan di awal paragraf hingga orientasi ditemukan, dan saya berhenti di sana.

3. Yang lainnya

Jadi, saya sampai pada tahap akhir desain, setelah bermain cukup dengan manipulator dan membungkus IMU-sensor. Saat mengerjakan dua langkah sebelumnya, saya sudah memiliki ide yang jelas tentang bagaimana semuanya akan bekerja dan dengan algoritma apa. Karena itu, saya menangani tahap ini dengan cukup cepat. Karena hanya orientasi telapak tangan yang diketahui, kami bekerja secara langsung dengan badan kerja, yang diperlukan untuk mengarahkannya. RO dapat mengambil arah apa pun, jika tidak melanggar area kerja (putar semua 360 tidak berfungsi).

Dalam item pengembangan manipulator, vektor PO diatur secara manual, dan setelah itu sudut rotasi drive ditemukan. Jadi, vektor ini harus ditentukan berdasarkan orientasi telapak tangan. Orientasi dapat diekspresikan sebagai dasar

E

$E$ menemukannya dengan mengubah angka empat menjadi matriks. Basis terdiri dari vektor-vektor kolom dari orths-nya, oleh karena itu, kami memperoleh tiga vektor

v e c x^{'}

$\ vec {x} '$ ,

v e c y^{'}

$\ vec {y} '$ dan

v e c z^{'}

$\ vec {z} '$ . Akan lebih mudah untuk menggunakan vektor sebagai orientasi

v e c x^{'}

$\ vec {x} '$ , karena saya mengasumsikan posisi awal manipulator, ketika semua tautan dan PO terletak di bidang XZ dari sistem koordinat basis, dan PO horizontal pada saat itu, mis. vektor

v e c v_{0}

$\ vec {v_0}$ pada awalnya, itu sejajar dengan sumbu X dari BSK dan NSC (kami memposisikan posisi awal modul SINS sehingga NSC bertepatan dengan BSK dari manipulator). Dalam hal ini, kolom pertama dari matriks

E

$E$ samakan vektor

v e c v_{0}

$\ vec {v_0}$ . Kemudian kita menormalkannya sepanjang PO dan mendapatkan vektor yang diperlukan relatif terhadap sistem koordinat dasar manipulator. Kemudian kita mengikuti urutan perhitungan koordinat umum dari hal.

Perlu dicatat bahwa manipulator, ketika mengubah orientasi RO, mampu bergerak dalam dua mode: pertama - ketika titik flensa diam, kedua - ketika titik akhir PO diam, tetapi orientasinya diamati. Mode kedua lebih menarik karena bahkan dengan tidak adanya gerakan linier, semua sumbu rotasi masih terlibat untuk memindahkan titik flensa, sambil mengamati orientasi PO. Namun, transisi dari mode pertama ke yang kedua terjadi dengan penambahan hanya satu operasi pengurangan vektor untuk menemukan vektor

v e c r

$\ vec {r}$ (lihat paragraf 1).

Semua operasi di atas juga diprogram dalam lingkungan Matlab. Secara umum, struktur program adalah sebagai berikut:

Kalibrasi saat startup. Kami mengatur seluruh peternakan ke posisi semula dan tanpa berani menyentuh, kalibrasi modul SINS untuk sejumlah data mentah darinya. Kalibrasi diperlukan, karena Anda perlu menghapus offset awal yang dihasilkan filter (saya tidak mengerti mengapa, dan itu berhasil dengan baik).
Awal naskah. Kami menginisialisasi semua pustaka dan variabel, mengatur posisi awal flange atau titik akhir PO.
Mulai siklus. Pada setiap iterasi, kami menginterogasi sensor, menemukan angka empat, menerjemahkannya ke dalam matriks, yang merupakan dasar $E$ , ini adalah dasar di mana RO berada. Kolom pertama diambil sebagai orientasi PO dan kami menemukan semua koordinat umum menggunakan pertimbangan matematika dari Bagian 1.
Mengetahui koordinat umum pada saat terakhir dan saat ini, kami menghitung kecepatan sudut rotasi sumbu.
Kami mengirim paket data ke mikrokontroler manipulator.

Tentu saja ini terlihat canggung, tetapi jika Anda melihat lebih dekat, Anda dapat melihat hasil positif dari penelitian ini. Pekerjaan ini, tentu saja, tidak berpura-pura selesai dan membutuhkan banyak upaya untuk disempurnakan, tetapi hanya jika ini dapat digunakan. Tetapi saya belum menemukan aplikasi spesifik ... Dapatkah seseorang memberi tahu saya?

Manipulasi "manual"

1. Perkembangan manipulator

Deskripsi matematis kinematika

2. Pengembangan perangkat untuk melacak pergerakan lengan

3. Yang lainnya

More articles: