Halo, Habr! Pada artikel ini saya akan berbicara tentang membuat model matematika dari pipa panjang untuk CAX-program SimulationX di Modelica. Ini akan menjadi pertanyaan tentang menghitung proses gelombang (tekanan pulsasi, water hammer, dll.) Dalam saluran hidrolik menggunakan metode karakteristik. Terlepas dari kenyataan bahwa metode ini cukup lama, tidak ada informasi yang cukup di RuNet tentang aplikasinya untuk memecahkan masalah yang diterapkan.

Di bawah potongan, saya akan mencoba menjelaskan mengapa perlu untuk memperhitungkan proses gelombang di jaringan pipa, untuk menyoroti masalah yang saya temui selama pemrograman dan pada akhirnya saya akan memberikan perbandingan dari proses denyut tekanan ketika pompa air tekanan tinggi tiga plunger beroperasi pada pipa panjang sederhana dalam model dan di stand URACA di Jerman.

Pendahuluan

Dalam praktik rekayasa, sebagai suatu peraturan, sedikit perhatian diberikan pada proses gelombang di jaringan pipa. Contoh paling terkenal, ketika proses gelombang merusak kehidupan seorang insinyur, adalah palu air:



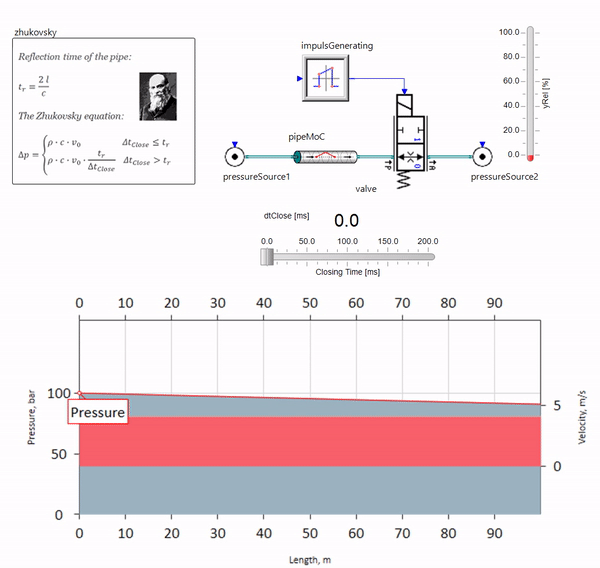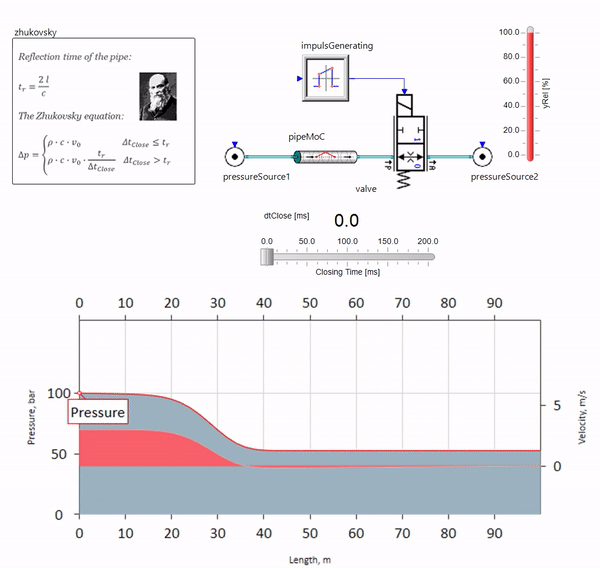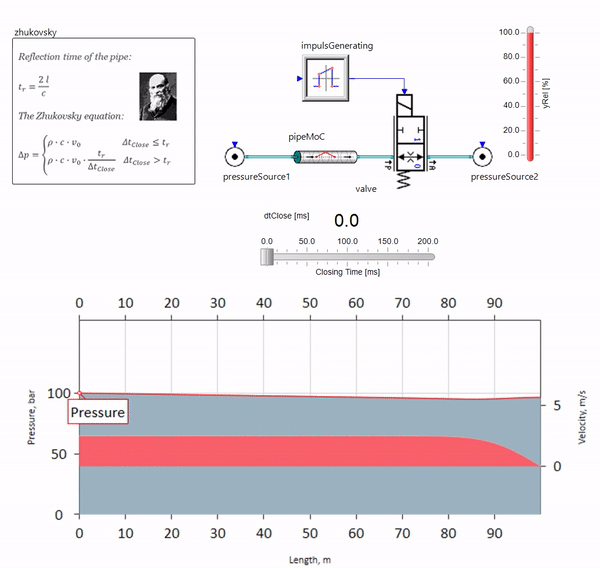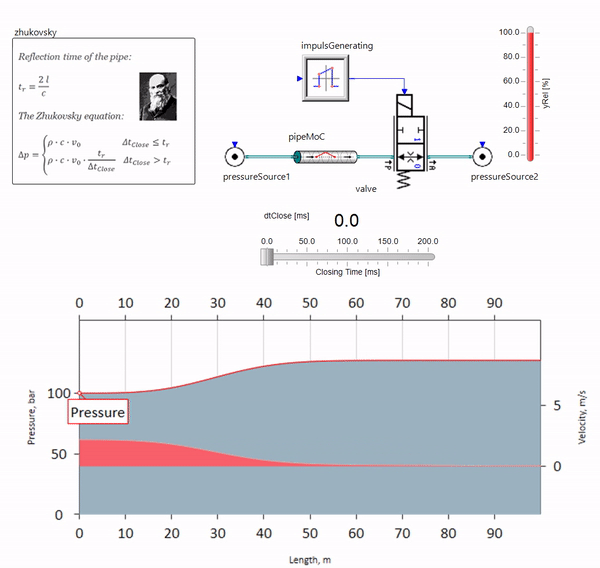
Ketika katup menutup dengan cepat di ujung pipa, hilir, terjadi gelombang tekanan yang bergerak ke atas pada kecepatan suara lokal (untuk air, sekitar 1.500 m / s), tercermin dari sumber tekanan konstan, kembali ke katup dan dipantulkan dari dia kali ini dengan tanda negatif. Proses ini diulang sampai semua energi dikeluarkan pada gesekan, dan sampai saat itu katup dan seluruh pipa mengalami beban kejut, amplitudo dan frekuensinya tergantung pada panjang pipa dan kecepatan awal aliran fluida.

Hydroblow dengan keakuratan yang diperlukan untuk menyelesaikan masalah-masalah praktis dideskripsikan pada akhir abad ke-19 oleh Nikolai Zhukovsky, dengan demikian menyelesaikan masalah kecelakaan di pasokan air Moskow. Sejak itu, rumus untuk menghitung lompatan tekanan ketika katup ditutup dengan cepat disebut rumus Zhukovsky di seluruh dunia:

$$

$$\ Delta p = \ rho \ cdot c \ cdot \ Delta v$$

Palu air dalam praktiknya memanifestasikan dirinya, sebagai suatu peraturan, dengan panjang pipa dari seratus meter. Pada panjang di bawah, sudah sulit untuk menemukan peralatan hidrolik yang bisa menutup lebih cepat daripada gelombang tekanan yang dilewati dari katup dan belakang (kondisi untuk terjadinya palu air). Namun demikian, bahkan perpipaan yang relatif singkat masih dapat merusak kehidupan insinyur jika sistem memiliki sumber aliran pulsasi (misalnya, pompa volumetrik dengan jumlah plunger yang terbatas).



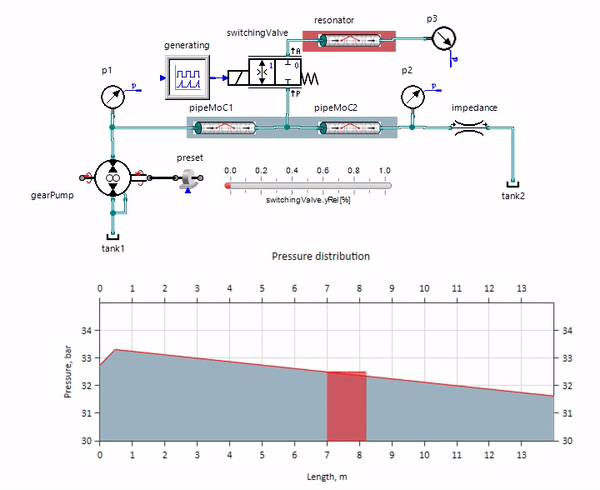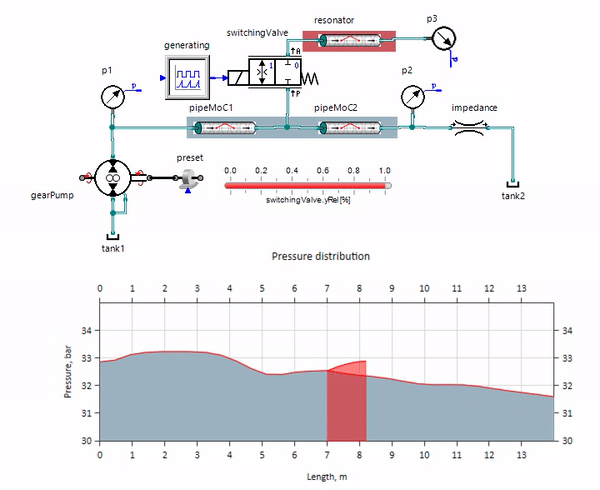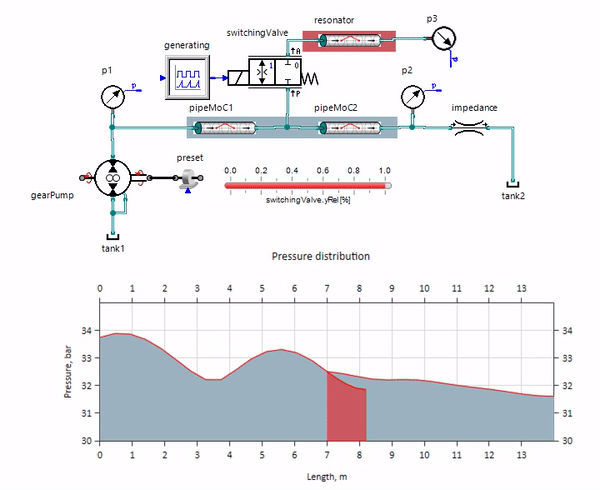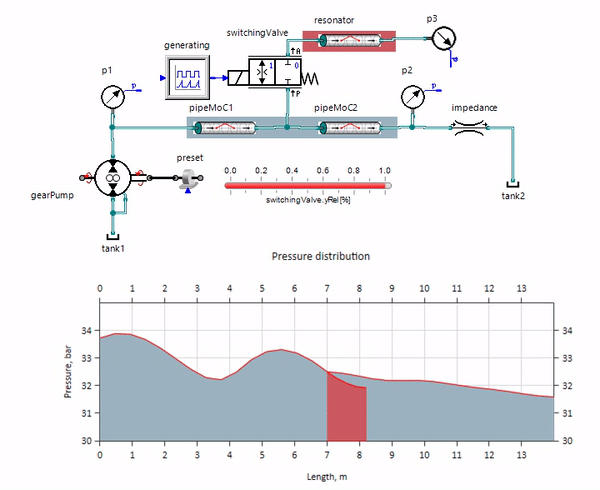
Gif menunjukkan efek menguntungkan dari sepotong pipa yang panjangnya hanya sekitar satu meter. Panjangnya sama dengan seperempat dari panjang gelombang tekanan, jadi ketika Anda menghubungkannya ke pipa utama, yang disebut gelombang berdiri, yang secara antiphase mengenai sumber denyut dan menekannya dengan cara ini (inilah yang disebut peredam denyut gelombang seperempat). Jelaslah bahwa dengan kombinasi keadaan yang tidak menguntungkan, efeknya mungkin sebaliknya.

Dalam latihan saya, saya mencoba untuk waktu yang lama untuk mengesampingkan proses gelombang, karena perhitungan mereka membutuhkan pemahaman yang lebih mendalam tentang metode matan dan numerik, yang selama studi saya saya perlakukan dengan pengabaian. Tetapi ketika suatu hari saya melihat dengan mata kepala sendiri bahwa saran standar (untuk menempatkan HPP, akumulator hidrolik, untuk mengatur cadangan di inlet pompa) tidak membantu menyingkirkan denyut di bangku, atau, lebih lagi, membawa mereka lebih dekat untuk memahami proses, saya harus masuk lebih dalam ke matras . Khususnya untuk rasa malu saya, penyelia riset saya sudah mulai menulis model pipa di C ++ untuk saya.

1. Model satu dimensi dari saluran hidrolik dalam parameter terdistribusi

Masalah utama yang membuat model satu dimensi tradisional yang dijelaskan oleh persamaan diferensial biasa melampaui zona kenyamanan adalah bahwa pipa paling sederhana, bahkan dengan asumsi yang paling mengerikan (diisi penuh dengan cairan, memiliki panjang penampang yang konstan, kecepatan fluida dirata-ratakan di atas penampang, proses perpindahan panas tidak dipertimbangkan) dijelaskan oleh persamaan diferensial dalam parameter terdistribusi (persamaan Euler, hanya memperhitungkan gaya massa dan gesekan di sisi kanan yang kedua avneniya):

$$

$$\ frac {\ partial \ rho} {\ partial t} + \ frac {\ partial (\ rho v)} {\ partial x} = 0,$$

$$

$$\ frac {\ partial (\ rho v)} {\ partial t} + \ frac {\ partial (\ rho v ^ 2 + p)} {\ partial x} = \ rho \ cdot (G + F),$$

dimana $$$\ rho$- kepadatan $$$v$- kecepatan $$$p$- tekanan $$$F$- kerugian gesekan, $$$G$- Penurunan tekanan yang disebabkan oleh gaya gravitasi.

Yaitu mengintegrasikan sekarang Anda tidak hanya membutuhkan waktu $$$t$tetapi juga dalam koordinat spasial $$$x$.
Dalam hal cairan, Anda dapat menyederhanakan hidup Anda sedikit lebih banyak jika Anda menulis ulang persamaan dari variabel konservatif ke variabel primitif (kecepatan dan tekanan):

$$

$$\ frac {\ partial p} {\ partial t} + v \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x } = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} + v \ frac {\ displaystyle \ partial v} {\ displaystyle \ partial x} = F + G$$

dimana $$$c$- kecepatan suara.

Sekarang, jika kita menerima bahwa kecepatan suara secara signifikan lebih besar daripada kecepatan pergerakan cairan $$$v \ ll c$(yang benar jika tidak ada kavitasi), persamaan akan menjadi sedikit lebih sederhana:

$$

$$\ frac {\ partial p} {\ partial t} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x} = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} = F + G$$

Untuk menyelesaikan persamaan ini, dengan satu atau lain cara, singkirkan diferensiasi dalam koordinat spasial $$$x$. Ini dapat dilakukan secara langsung jika Anda mengganti diferensial spasial dengan skema beda hingga, dan dalam hal waktu, maka langsung saja menuju diferensial penuh, dengan mengatakan bahwa di dalam sel yang sama, parameter keadaan tidak bergantung pada koordinat:

$$

$$\ frac {dp} {dt} = - \ rho \; c ^ 2 \ frac {\ triangle v} {\ triangle x}$$

$$

$$\ frac {dv} {dt} = F + G- \ frac1 \ rho \ frac {\ displaystyle \ triangle p} {\ displaystyle \ triangle x}$$

Sekarang persamaan ini dapat diselesaikan sebagai persamaan diferensial biasa, membagi panjang pipa menjadi banyak volume hingga. Jadi ini dilakukan , misalnya, dalam paket Simscape, di MATLAB Simulink, dan masalahnya diselesaikan hingga saat ini di SimulationX .
Sesuatu dengan cara ini, tentu saja, dapat dihitung, tetapi fluktuasi numerik yang muncul dalam kasus ini sangat terhalang:

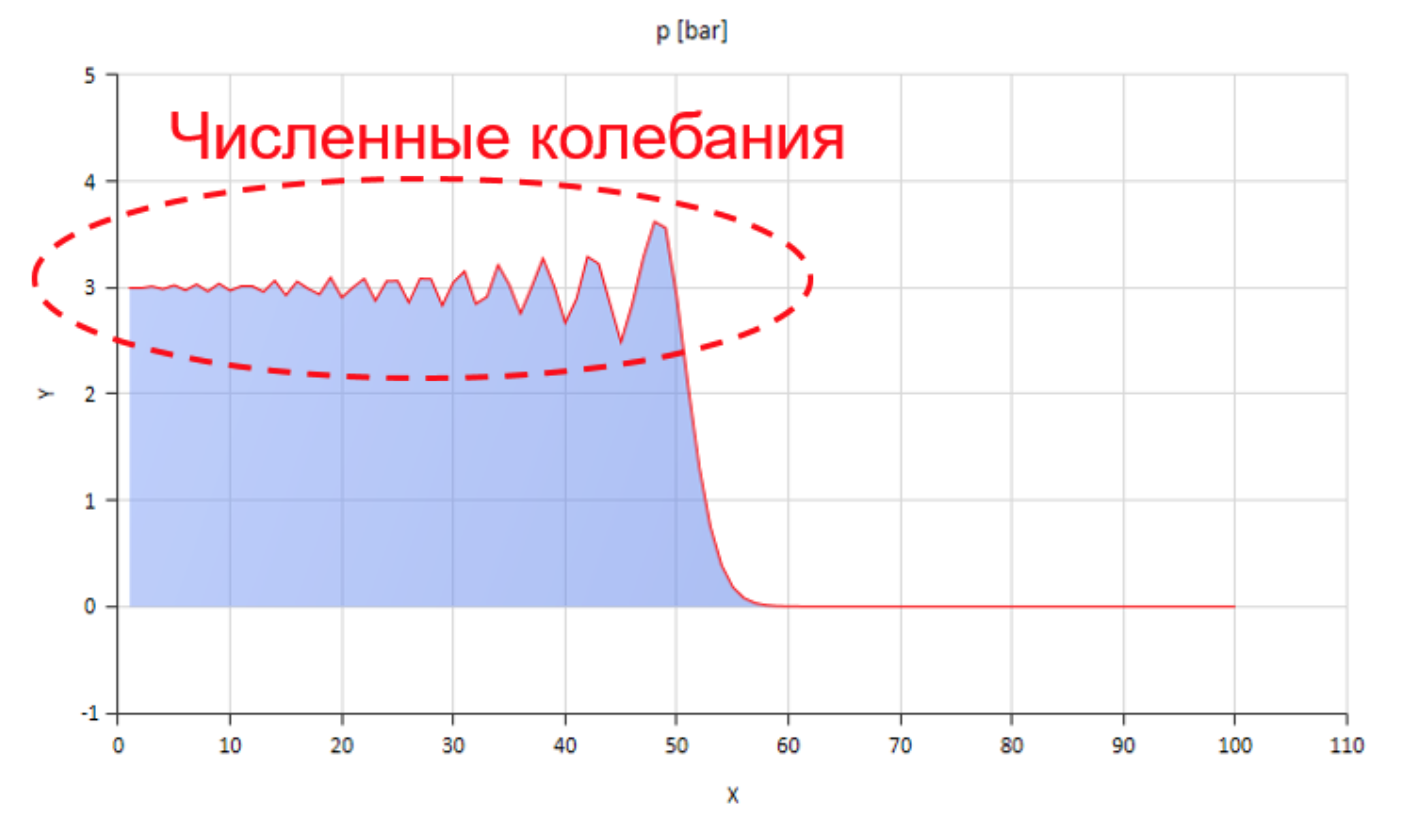Gambar tersebut menunjukkan bagian depan gelombang tekanan bergerak dari kiri ke kanan.

Anda dapat menangani osilasi ini, misalnya, memperkenalkan difusi numerik, tetapi kemudian kecepatan rambat gelombang terdistorsi secara signifikan. Anda dapat meningkatkan gesekan (terutama membantu meningkatkan komponen non-stasionernya), tetapi kemudian model tersebut berhenti mencerminkan esensi fisik.

Cara terbaik adalah menggunakan metode berbeda untuk mengubah persamaan dalam parameter terdistribusi menjadi persamaan diferensial biasa, misalnya, metode karakteristik.

2. Metode karakterisasi

Wikipedia merekomendasikan "Metode Karakteristik" merekomendasikan:

... untuk menemukan karakteristik di mana persamaan diferensial parsial berubah menjadi persamaan diferensial biasa. Segera setelah persamaan diferensial biasa ditemukan, mereka dapat diselesaikan sepanjang karakteristik dan solusi yang ditemukan dapat diubah menjadi solusi dari persamaan diferensial parsial asli.

Ini seperti batu filsuf, tetapi alih-alih mengubah logam menjadi emas, kami mengubah persamaan diferensial parsial menjadi persamaan biasa, dan sebaliknya. Timbul pertanyaan: "bagaimana menerapkan ini dalam praktek?", Dan lebih disukai lebih efektif daripada alkemis abad pertengahan ...

Untuk memulainya, kita akan memahami pernyataan masalah. Pada saat awal, kami memiliki semacam distribusi tekanan dan kecepatan di sepanjang pipa. Pertama, kami memecah pipa menjadi sejumlah elemen yang terbatas dan memberikan nilai tekanan untuk setiap permukaan $$$p_i$dan kecepatan $$$v_i$.


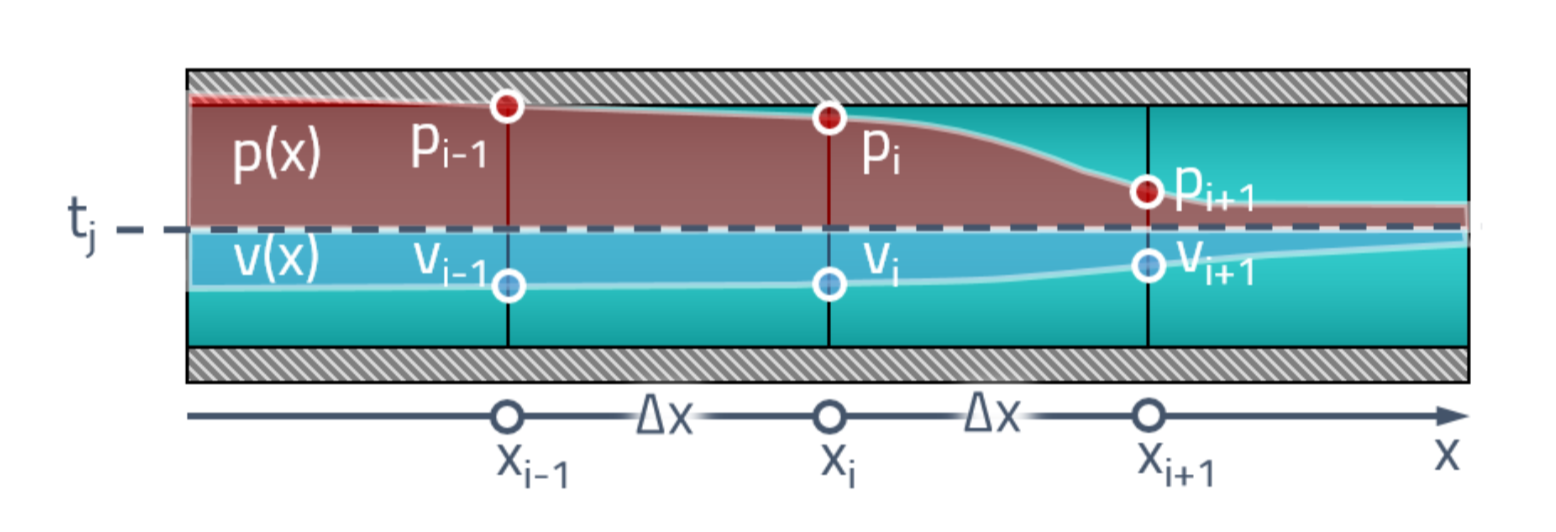
Kami tertarik pada bagaimana nilai-nilai pada titik-titik ini berubah seiring waktu $$$\ triangle t$. Maju cepat ke ruang-waktu dan tempatkan keadaan pipa di masa depan di atas keadaan awal:



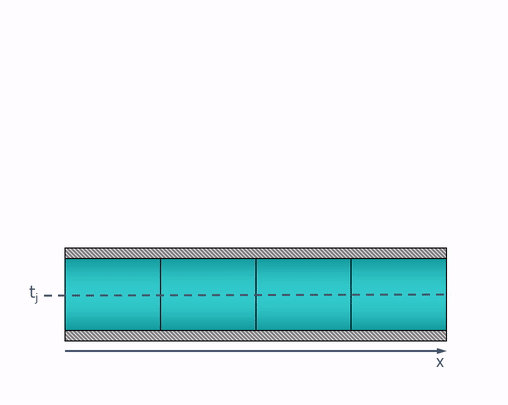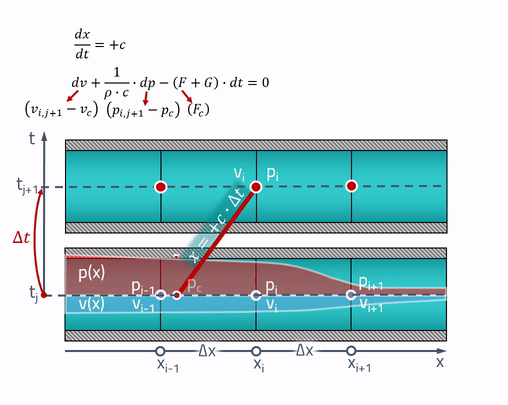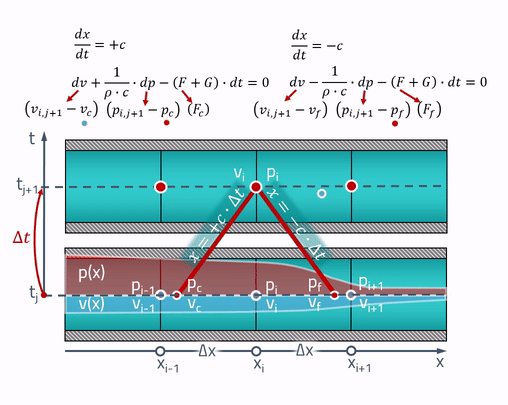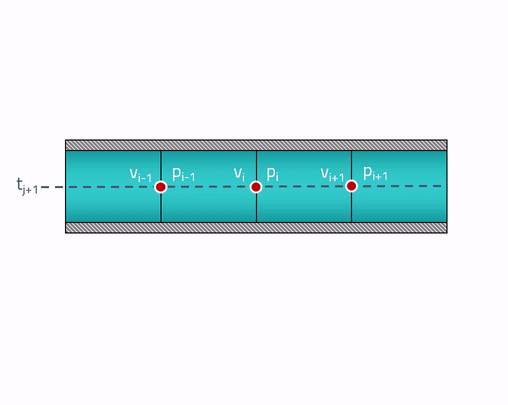
Di sinilah karakteristik "sihir" berguna! Penjelasan petani yang bekerja adalah bahwa semua perubahan dalam pipa terjadi pada kecepatan suara. Tekanan dan kecepatan pada titik saat ini $$$i$tergantung pada tekanan dan kecepatan pada titik-titik di pipa di mana gelombang suara itu (akan) $$$\ triangle t$beberapa detik yang lalu. Ini diilustrasikan sebagai berikut:



Dua garis simetris diambil dari titik mana pun, kemiringannya ditentukan oleh kecepatan suara. Ini adalah karakteristik di mana persamaan diferensial parsial berubah menjadi persamaan diferensial biasa. Jika kita menyebutkan titik-titik di mana karakteristik berpotongan dengan keadaan pipa di masa lalu sebagai $$$c$dan $$$f$, persamaan ditulis sebagai berikut:

$$

$$dv + \ frac1 {\ rho c} dp- (F + G) dt = 0 \; untuk \; \ frac {dx} {dt} = + c$$

$$

$$dv- \ frac1 {\ rho c} dp- (F + G) dt = 0 \; untuk \; \ frac {dx} {dt} = - c$$

Nilai-nilai tekanan dan kecepatan pada titik-titik ini dapat diperoleh dengan interpolasi linier antara nilai-nilai parameter keadaan di grid:


Penting untuk mempertimbangkan bahwa titik-titik ini harus selalu berada dalam sel tetangga! Untuk ini, langkah waktu harus memenuhi kriteria Courant - Friedrichs - Levy (CFL):

$$

$$\ triangle t <\ frac {\ triangle x} c$$

Sekarang, setidaknya skema perbedaan paling sederhana dapat diterapkan pada persamaan ini:

$$

$$(v_ {i, \; j + 1} -v_c) + \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_c) - (F + G) \ segitiga t = 0$$

$$

$$(v_ {i, \; j + 1} -v_f) - \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_f) - (F + G) \ segitiga t = 0$$

Dalam sistem yang dihasilkan dari dua persamaan, dua tidak diketahui: tekanan $$$p_ {i, \; j + 1}$dan kecepatan $$$v_ {i, \; j + 1}$. Anda dapat menyelesaikannya secara numerik, tetapi tidak ada masalah khusus untuk mendapatkan solusi analitis. Kemudian, jika kita menerima keteguhan kecepatan suara, kita mendapatkan skema perbedaan yang sepenuhnya eksplisit.

Untuk mengkonsolidasikan, saya akan memberikan animasi dari metode karakteristik:

3. Eksperimen

Saya berkesempatan untuk akhirnya mengingat modelnya ketika saya mulai bekerja di ESI ITI GmbH di Dresden. Suatu kali, saya menerima tiket di Helpdesk, di mana para insinyur URACA mengeluh bahwa mereka tidak dapat mencapai konvergensi dengan eksperimen dengan pipa "lama" kami.
Mereka membuat pompa pendorong air bertekanan tinggi, “Karcher” yang sangat besar, dan ingin dapat memprediksi efek resonansi yang mungkin karena mencakup proses gelombang dalam pipa. Masalahnya adalah pompa seperti itu, sebagai suatu peraturan, memiliki sangat sedikit penyedot dan mereka beroperasi pada kecepatan rendah (250-500 rpm):



Karena ini, dan juga karena pengaruh kompresibilitas cairan, output alirannya sangat tidak merata:



Kesenjangan dan non-linearitas membuatnya sulit untuk linierisasi dan menganalisis model dalam domain frekuensi, dan perhitungan CFD untuk tugas semacam itu adalah menembak dari meriam di burung pipit. Selain itu, mereka sudah memiliki model di SimulationX, di mana mereka memperhitungkan dinamika bagian mekanis pompa, elastisitas rangka, dan karakteristik motor listrik, sehingga akan menarik untuk melihat bagaimana pipa mempengaruhi ini.

Tata letak bangku tes cukup sederhana:



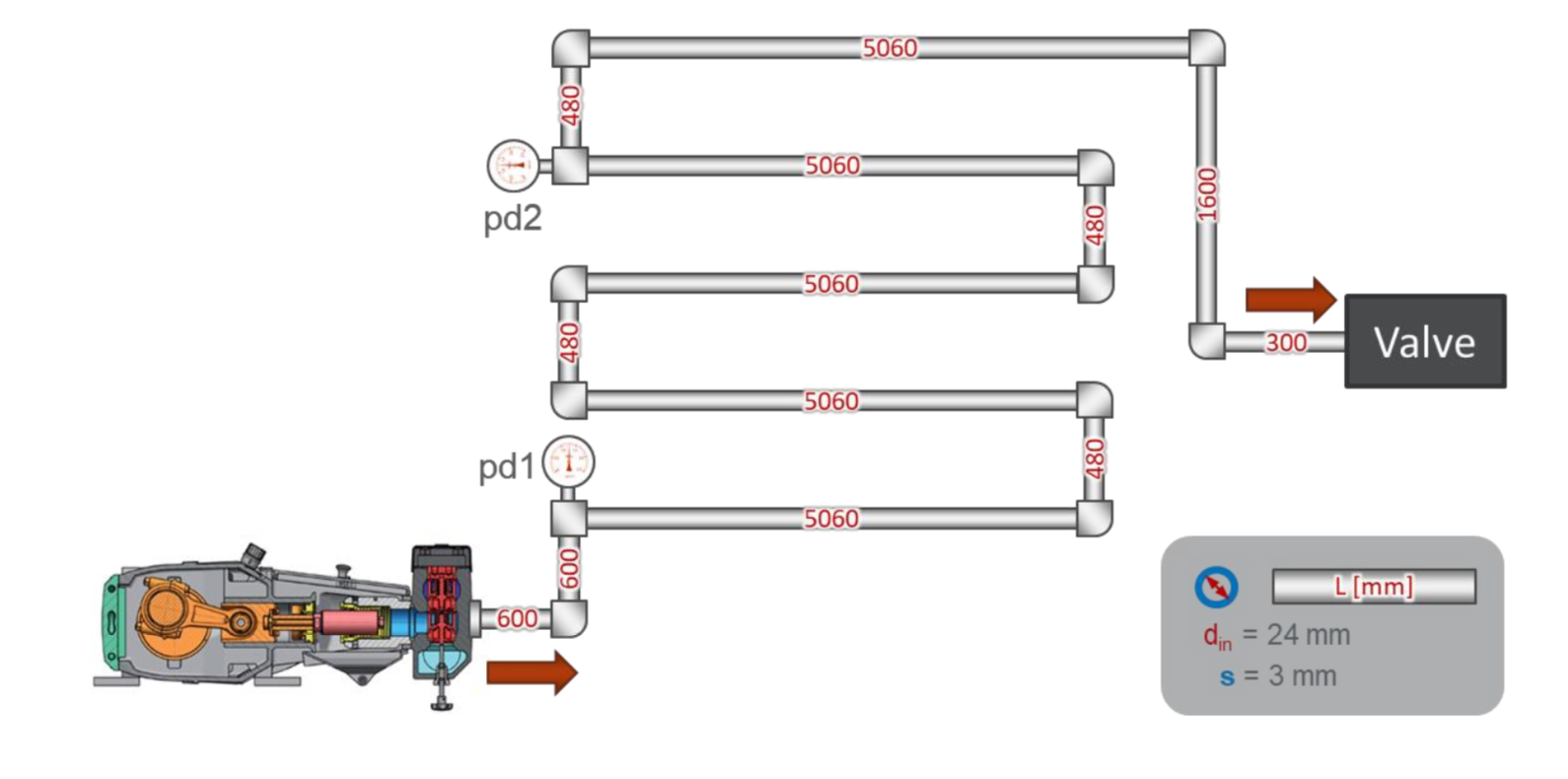
Ada pipa sederhana dengan total panjang sekitar 30 meter. Pada awal pipa, sensor tekanan pd1 dipasang, pada jarak 22 meter darinya - sensor tekanan pd2. Di ujung pipa adalah katup yang mengatur tekanan dalam sistem.

Saya menyarankan untuk menguji versi beta dari model saya, karena model seperti itu dibuat di SimulationX:



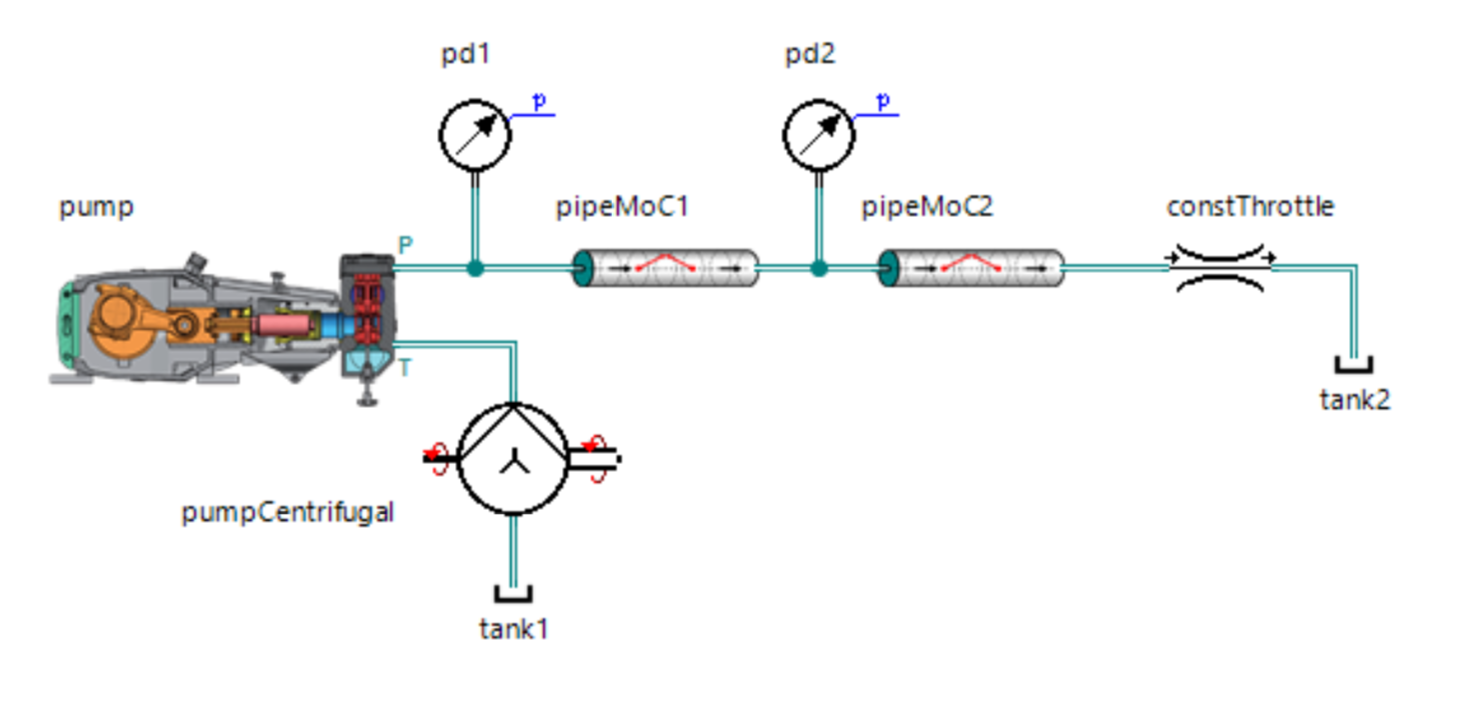
Hasilnya bahkan mengejutkan saya:




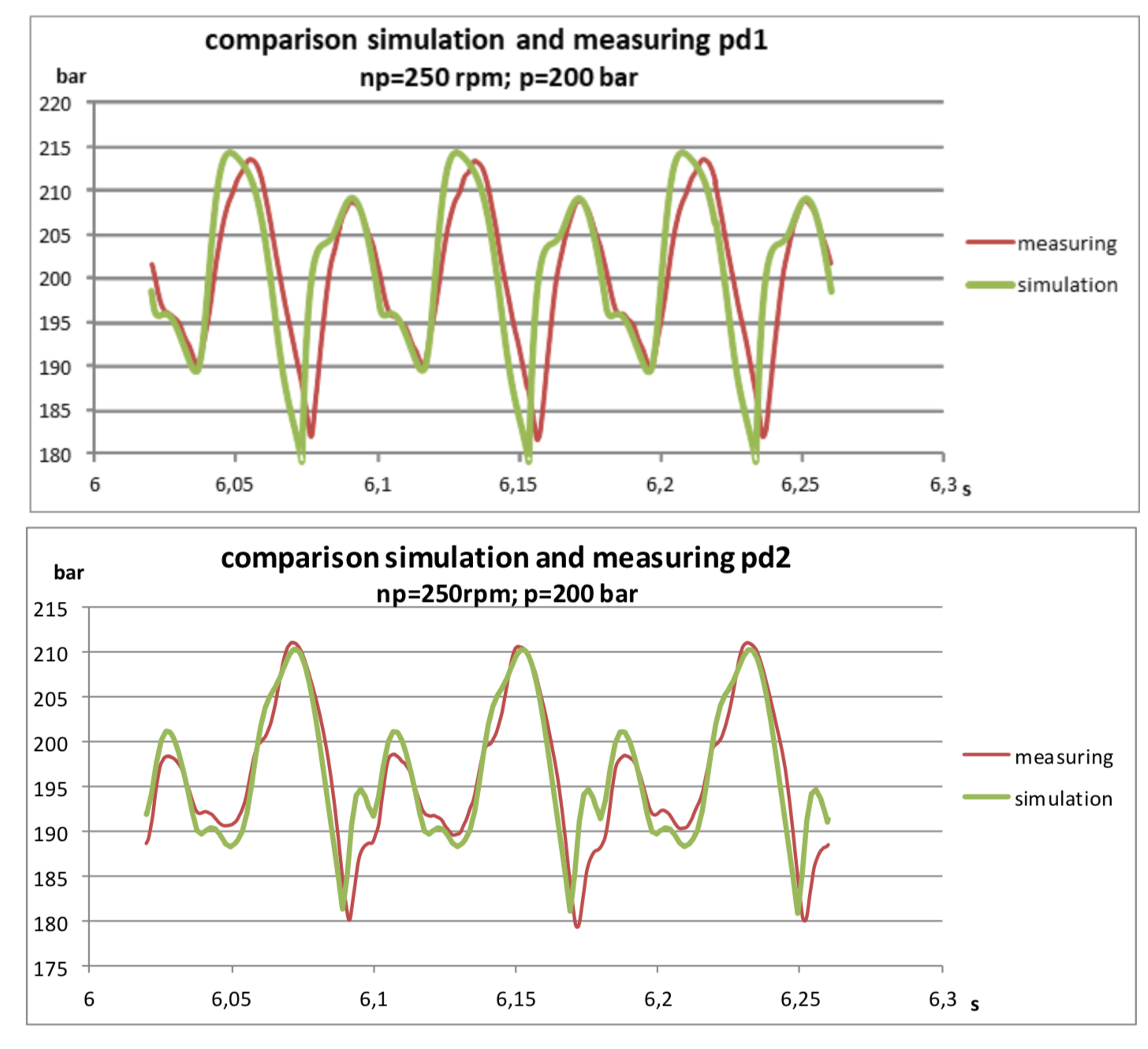
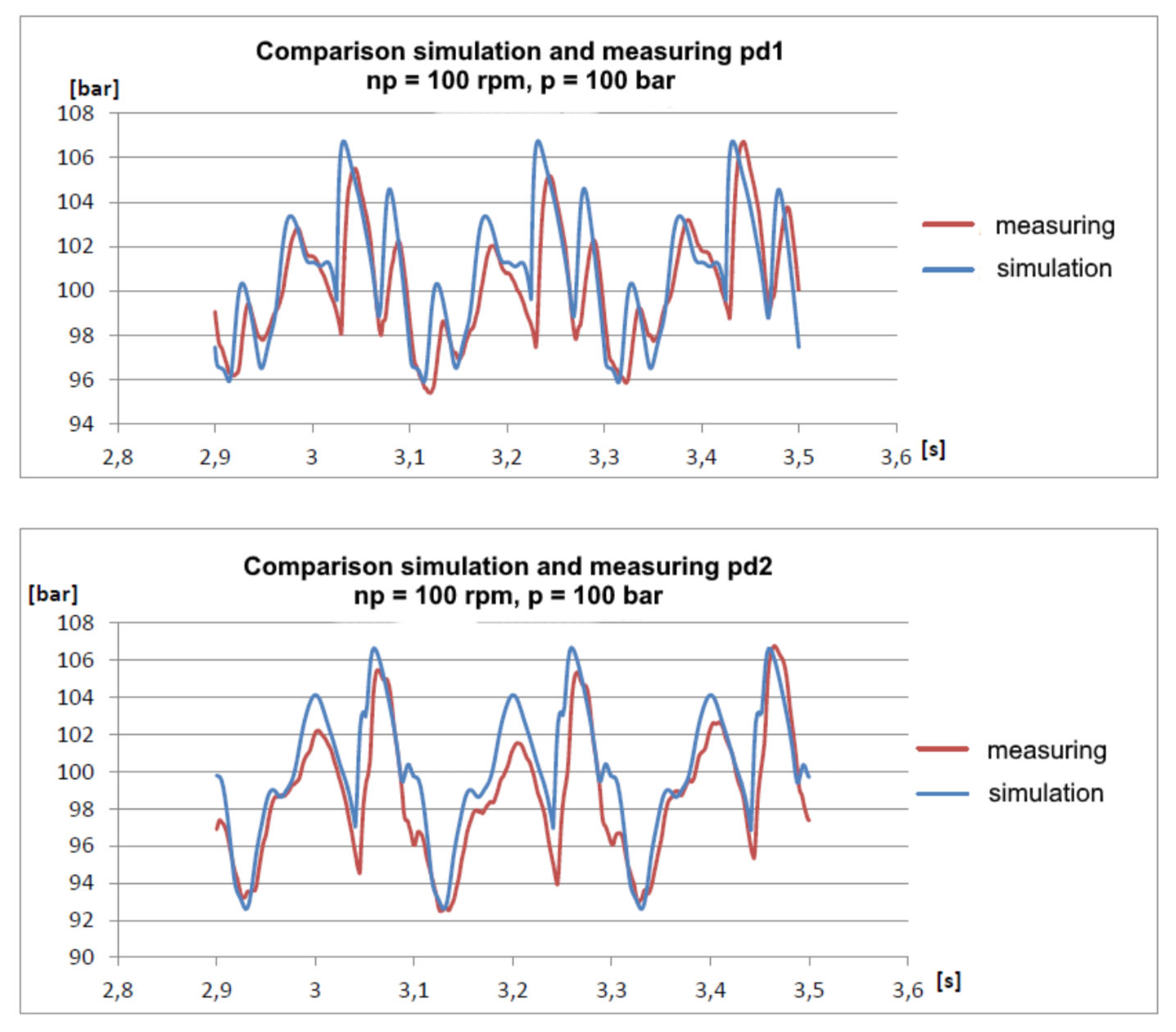
Dapat dilihat bahwa model ini sedikit teredam, yang dapat dimengerti asalkan tidak memperhitungkan hambatan hidrolik. Namun demikian, harmonisa dasar cukup baik secara kebetulan dan memungkinkan untuk memprediksi amplitudo tekanan dengan akurasi yang cukup baik.

Pengalaman ini memungkinkan saya untuk dengan cepat meluncurkan model baru dari saluran hidrolik dalam rilis SimulasiX, dan saya terjun ke topik ini dan tidak melihat bagaimana, bersama dengan siswa-magang, saya juga melihat model saluran pneumatik, di mana semuanya jauh lebih menarik. Di sana, saya harus menggunakan metode yang didasarkan pada metode Godunov, yang pada gilirannya didasarkan pada solusi dari masalah Riemann dari peluruhan diskontinuitas yang sewenang-wenang, yah, tentang ini sudah entah bagaimana lain kali ...

Sastra

1. Dalam literatur domestik, metode karakteristik untuk aplikasi teknik paling baik dijelaskan dalam buku "Hydromechanics", D. N. Popov, S. S. Panaiotti, M. V. Ryabinin.
2. Dalam terbitannya
   Simulasi perpipaan dengan metode karakteristik untuk menghitung denyut tekanan dari pompa pendorong air bertekanan tinggi

   "Dr.-Ing. (Rus) Maxim Andreev, Dipl.-Ing. Uwe Grätz dan Dipl.-Ing. (FH) Achim Lamparter ”, Konferensi Kekuatan Fluida Internasional ke-11, 11. IFK, 19-21 Maret 2018, Aachen, Jerman, silakan lihat teks dalam PM
   Saya memeriksa lebih detail masalah-masalah yang berhubungan dengan metode karakteristik dan pemecah ODE.
3. Siapa yang memiliki akses ke perpustakaan Jerman, ikhtisar terbaik dari metode untuk menyelesaikan persamaan hiperbolik sebagaimana diterapkan pada saluran hidrolik yang saya temui terkandung dalam disertasi berikut: Beck, M., Modellierung und Simulation der Wellenbewegung di kavitierenden Hydraulikleitungen, Univ. Stuttgart, Jerman, 2003.
4. Klasik dari genre persamaan hiperbolik secara umum: Randall J. Leveque, Metode Volume Hingga untuk Masalah Hiperbolik, Cambridge University Press, Cambridge, Inggris, 2002.