Halo, Habr!

Tiga tahun lalu, di situs Leonid Zhukov, saya menyodok tautan ke jalur Yure Leskovek cs224w Analisis Jaringan dan sekarang kami akan membawanya bersama dengan semua orang dalam obrolan nyaman kami di saluran # class_cs224w. Segera setelah pemanasan dengan kursus pembelajaran mesin terbuka yang dimulai dalam beberapa hari.

Pertanyaan: Apa yang mereka baca di sana?
Jawab: Matematika modern. Kami menunjukkan contoh meningkatkan proses perekrutan TI.

Di bawah kucing pembaca, ada cerita tentang bagaimana matematika diskrit memimpin manajer proyek ke jaringan saraf, mengapa ERP dan manajer produk harus membaca majalah Bioinformatika, bagaimana tugas merekomendasikan koneksi muncul dan diselesaikan, siapa yang butuh embedding grafik dan dari mana asalnya, serta pendapat bahwa bagaimana berhenti takut pada pertanyaan tentang pohon di wawancara, dan berapa biaya semua ini. Ayo pergi!

Rencana kami adalah sebagai berikut:

1) Apa itu cs224w
2) Kotak-kotak atau naik
3) Bagaimana saya mendapatkan semua ini?
4) Mengapa membaca majalah bioinformatika
5) Apa itu embedding grafik dan dari mana asalnya
6) Kereta dorong acak dalam bentuk matriks
7) Kembalinya kereta dorong acak dan kekuatan ikatan
8) Jalur tramp acak dan bagian atas dalam vektor
9) Hari-hari kita adalah gelandangan acak untuk semua orang
10) Bagaimana dan di mana menyimpan data tersebut dan di mana mendapatkannya
11) Apa yang harus ditakuti
12) Memo ke pemain

Apa itu cs224w

Kursus Yure Leskovek Analisis Jaringan menonjol di galaksi produk pendidikan dari Fakultas Ilmu Komputasi di Universitas Stanford. Perbedaan dari yang lain adalah bahwa program tersebut mencakup berbagai masalah yang sangat luas. Ini adalah sifat interdisipliner yang membuat petualangan menjadi tantangan. Hadiah adalah bahasa universal untuk deskripsi sistem kompleks - teori grafik, yang dapat ditangani dalam sepuluh minggu.

Kursus ini tidak menghabiskan biaya sebanyak itu, tetapi membuka program Sertifikat Pascasarjana Kumpulan Data Masif , yang masih memiliki banyak barang.

Kedua dalam petualangan ini adalah CS229 Machine Learning Andrew Eun, yang tidak perlu diiklankan.

Ini diikuti oleh Kumpulan Data Massive CS246 Mining Jure Leskoveka, di mana mereka yang ingin diundang untuk beristirahat di MapReduce dan Spark.

Chris Manning mengakhiri perjamuan Pengambilan Informasi dan Pencarian Web CS276.

Sebagai bonus, CS246H Mining Set Massive Data Sets: Hadoop Labs dirancang khusus untuk mereka yang sedikit. Sekali lagi mengunjungi Yure.

Secara umum, mereka berjanji bahwa mereka yang telah lulus program akan memperoleh keterampilan dan pengetahuan yang cukup untuk mencari informasi di Internet (tanpa Google dan orang lain seperti mereka).

Naik atau biji

Sekali waktu, pemimpin dan mentor saya, pada saat itu - STO di Ukraina Nestlé, menjelaskan kepada saya, muda dan ambisius, mencoba untuk mendapatkan gelar MBA untuk menjadi bahkan bintang, kebenaran bahwa pengalaman dan pengetahuan membeli dan menjual di pasar tenaga kerja, dan tidak ijazah dan hasil tes.

Spesialisasi yang dijelaskan di atas dapat diselesaikan secara online dengan biaya $ 18.900 secara simbolis.

Rata-rata, sebuah petualangan membutuhkan waktu 1-2 tahun, tetapi tidak lebih dari 3. Untuk mendapatkan sertifikat, Anda harus menyelesaikan semua kursus dengan peringkat minimal B (3.0).

Ada cara lain.

Semua materi kursus Jure Leskovek diterbitkan secara terbuka dan sangat cepat. Karena itu, mereka yang berharap dapat menderita kapan saja, mengoordinasikan beban dengan kemampuan. Terutama berbakat saya sarankan mencoba mode petualangan "Ini Stanford, sayang!" - lulus paralel dengan kursus - video ceramah diposting dalam beberapa hari, literatur tambahan tersedia segera, pekerjaan rumah dan solusi terbuka secara bertahap.

Musim ini, setelah akhir Kursus Pembelajaran Mesin Terbuka tentang Habré , yang berguna untuk pemanasan, kami akan mengatur balapan di kelas saluran khusus # cs_cs224w ods.ai.

Disarankan untuk memiliki serangkaian keterampilan berikut:

• Dasar-dasar Ilmu Komputasi pada tingkat yang cukup untuk menulis program non-sepele.
• Dasar-dasar teori probabilitas.
• Dasar-dasar aljabar linier.

Bagaimana saya bisa melakukan semua ini?

Dia hidup untuk dirinya sendiri, tidak repot. Proyek implementasi SAP yang dikelola. Kadang-kadang - ia bertindak sebagai pelatih bermain di spesialisasi utamanya - dan CRM memutar kacang. Bisa dibilang hampir tidak menyentuh siapa pun. Saya terlibat dalam pendidikan mandiri. Pada titik tertentu, saya memutuskan untuk berspesialisasi dalam bidang transformasi bisnis (atau melakukan perubahan organisasi). Tugas menganalisis organisasi sebelum dan sesudah perubahan adalah bagian penting dari pekerjaan ini. Mengetahui di mana dan di mana harus berubah sangat membantu. Memahami hubungan antara orang-orang adalah faktor keberhasilan yang signifikan. Dia menghabiskan beberapa tahun mempelajari metodologi "lunak" untuk meneliti organisasi, tetapi dia masih tidak bisa puas dengan pertanyaan: "Siapa yang akan menjemput siapa: komandan kepala akuntan kepala, atau apakah itu lebih kuat daripada sisa gudang?" Saya telah bertanya-tanya selama beberapa tahun berturut-turut. Saya mencari cara untuk mengukur dengan pasti.

2014 adalah titik balik, ketika saya meninggalkan impian saya untuk MBA dan memilih statistik dan manajemen informasi di University of Lisbon yang baru (departemen telekomunikasi pertama dan sekarang yang masih hidup dari fakultas sistem penerbangan dan ruang angkasa di Universitas Politeknik Kiev) sebagai yang tertinggi kedua (saya mendengar drum roll) + Departemen Komunikasi di militer).

Pada semester pertama hakim kedua, ia mencoba analisis jejaring sosial - salah satu aplikasi teori grafik. Saat itulah saya mengetahui bahwa itu adalah sesuatu yang, ternyata, ada algoritma yang memecahkan masalah seperti siapa yang akan berteman dengan seseorang terhadap penerapan teknologi baru, tetapi saya tidak tahu sebelumnya dan mengeringkan kepala saya, menganalisis koneksi orang-orang di pikiran saya - itu benar-benar membengkak dari ini. Ternyata secara kebetulan bahwa analisis jaringan, setelah langkah pertama, adalah penggalian data dan pembelajaran mesin secara terus-menerus, baik dengan guru atau tanpa.

Pada awalnya, ada cukup klasik.

Saya menginginkan lebih. Untuk menangani embeddings (dan untuk memotong pekerjaan Marinka Zhitnik untuk tugas-tugas mereka), saya harus mempelajari pembelajaran yang mendalam, yang sangat terbantu oleh kursus Deep Learning di jari . Mengingat kecepatan kelompok Leskovek menciptakan pengetahuan baru, untuk menyelesaikan tugas-tugas manajerial secara otomatis, cukup dengan memantau pekerjaan mereka.

Mengapa membaca majalah bioinformatika

Membangun tim bukanlah tugas yang mudah. Siapa yang tidak boleh ditempatkan di kapal yang sama dengan salah satunya adalah salah satu masalah yang mendesak. Apalagi ketika wajah-wajah baru. Dan daerah itu tidak dikenal. Dan untuk menuju ke pantai yang jauh Anda tidak perlu satu perahu, tetapi seluruh armada. Dan di tengah jalan, interaksi yang erat diperlukan baik di kapal maupun di antara mereka. Hari kerja biasa implementasi SAP , ketika Pelanggan perlu mengirimkan sistem yang dikonfigurasikan untuk spesifiknya dari banyak modul, dan rencana proyek terdiri dari ribuan baris. Untuk semua pekerjaannya, dia tidak pernah mempekerjakan siapa pun - mereka selalu mengeluarkan tim. Anda adalah manajer proyek, Anda memiliki kekuatan, dan berbalik. Sesuatu seperti itu. Diputar keluar.

Contoh hidup:

Saya sendiri tidak mewawancarai, tetapi saya mengalokasikan Timlids untuk ini. Dan untuk sumber daya - permintaan dari saya. Dan integrasi anggota tim baru juga merupakan tanggung jawab manajer proyek. Saya percaya bahwa banyak orang akan setuju bahwa semakin baik mempersiapkan daftar kandidat, semakin menyenangkan proses untuk semua peserta. Kami akan mempertimbangkan tugas ini secara rinci.

Diperlukan kemalasan alami - temukan cara untuk mengotomatisasi. Menemukannya Saya berbagi.

Sedikit teori manajemen. Metodologi Adizes didasarkan pada prinsip dasar: organisasi, seperti organisme hidup, memiliki siklus hidupnya sendiri dan menunjukkan manifestasi perilaku yang dapat diprediksi dan berulang selama pertumbuhan dan penuaan. Pada setiap tahap pengembangan organisasi, perusahaan mengharapkan serangkaian masalah tertentu. Seberapa baik manajemen perusahaan menangani mereka, seberapa berhasil itu membuat perubahan yang diperlukan untuk transisi yang sehat dari tahap ke tahap, dan menentukan keberhasilan atau kegagalan utama organisasi ini.

Saya telah terbiasa dengan ide-ide Yitzhak Adizes selama sekitar sepuluh tahun dan dalam banyak hal setuju.

Kepribadian karyawan - seperti vitamin - memengaruhi kesuksesan dalam kondisi tertentu. Ada contoh-contoh yang diketahui tentang bagaimana para pemimpin yang sukses, pindah dari satu industri, gagal di yang lain. Itu terjadi lebih buruk. Misalnya, Marissa Mayer, yang mengangkat pencarian Google, menjatuhkan Yahoo. Warren Buffett mengatakan dia tidak akan berhasil dilahirkan di Bangladesh. Lingkungan dan cara berinteraksi di dalamnya merupakan faktor penting.

Akan lebih baik untuk memprediksi komplikasi sebelum percobaan pada yang hidup, bukan?

Dalam garis besar ini terletak studi Marinka itnik selanjutnya yang diterbitkan dalam jurnal Bioinformatics. Tugas memprediksi efek samping dengan penggunaan kombinasi obat secara matematis dekat dengan manajerial. Semua berkat fleksibilitas bahasa grafik. Mari kita pertimbangkan lebih terinci.

Decagon graph convolutional network - alat untuk memprediksi koneksi dalam jaringan multimodal.

Metode ini terdiri dalam membangun grafik multimodal protein-protein, interaksi obat-protein, dan efek samping dari kombinasi obat, yang merupakan hubungan obat-obat, di mana masing-masing efek samping adalah tepi dari jenis tertentu. Decagon memprediksi jenis efek samping tertentu, jika ada, yang muncul dalam gambaran klinis.

Gambar tersebut menunjukkan contoh grafik efek samping yang diperoleh dari genom dan data populasi. Total - 964 jenis efek samping (ditunjukkan oleh tulang rusuk dari jenis ri, i = 1, ..., 964). Informasi tambahan dalam model disajikan dalam bentuk vektor sifat-sifat protein dan obat-obatan.

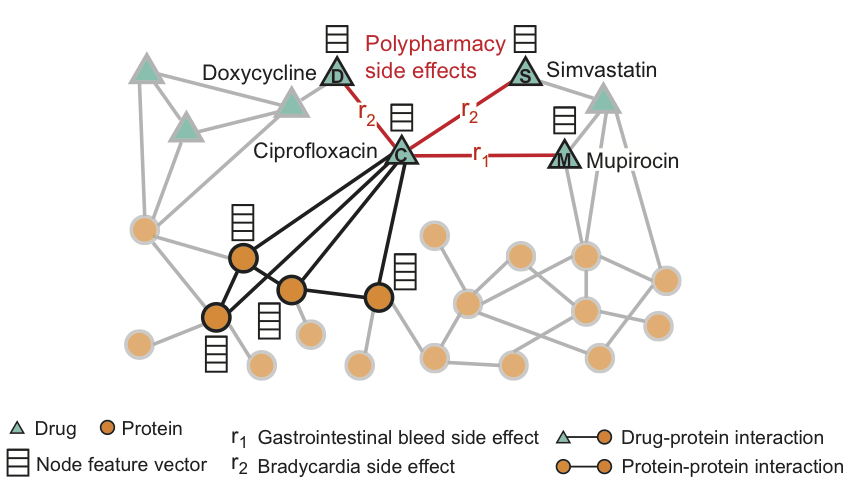
Untuk obat Ciprofloxacin (simpul C), tetangga yang disorot dalam grafik mencerminkan efek pada empat protein dan tiga obat lain. Kita melihat bahwa Ciprofloxacin (simpul C), yang diambil bersamaan dengan Doxycycline (simpul D) atau Simvastatin (simpul S), meningkatkan risiko efek samping memperlambat denyut jantung (efek samping seperti r2), dan kombinasi dengan Mupirocin (M) - meningkatkan risiko perdarahan saluran pencernaan (efek samping tipe r1).

Decagon memprediksi hubungan antara pasangan obat dan efek samping (ditunjukkan dengan warna merah) untuk mengidentifikasi efek samping dari penggunaan bersamaan, yaitu efek samping yang tidak dapat dikaitkan dengan salah satu obat dari pasangan secara terpisah.

Arsitektur grafik jaringan saraf convolutional neagon:

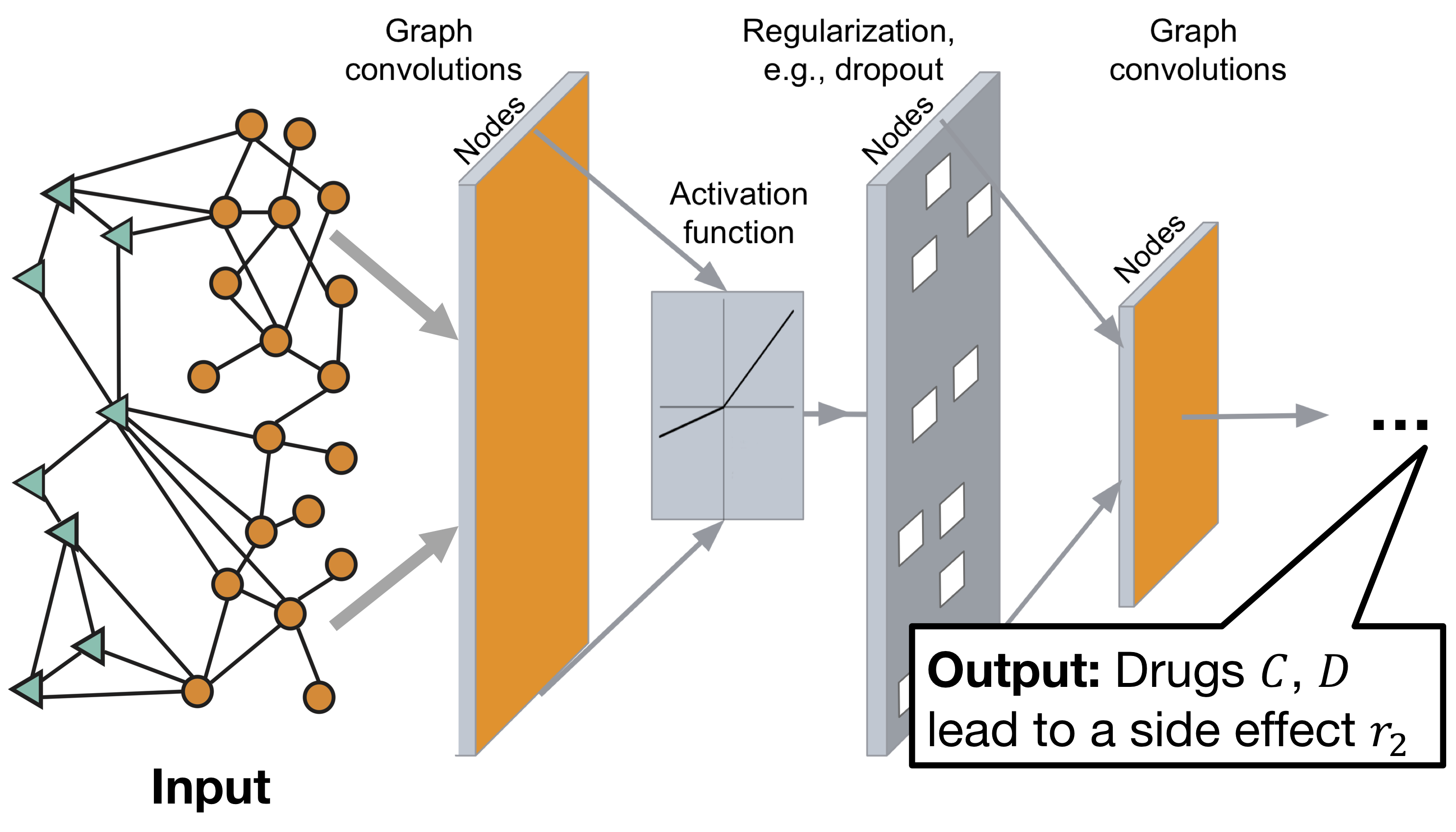
Model ini terdiri dari dua bagian:

Encoder: graph convolutional network (GCN) menerima grafik dan menyematkan node,
Decoder: Model faktorisasi tensor yang menggunakan embeddings ini untuk mendeteksi efek samping.

Informasi lebih lanjut dapat ditemukan di situs web proyek atau di bawah ini.

Bagus, tapi bagaimana cara mengikatnya dengan membangun tim?

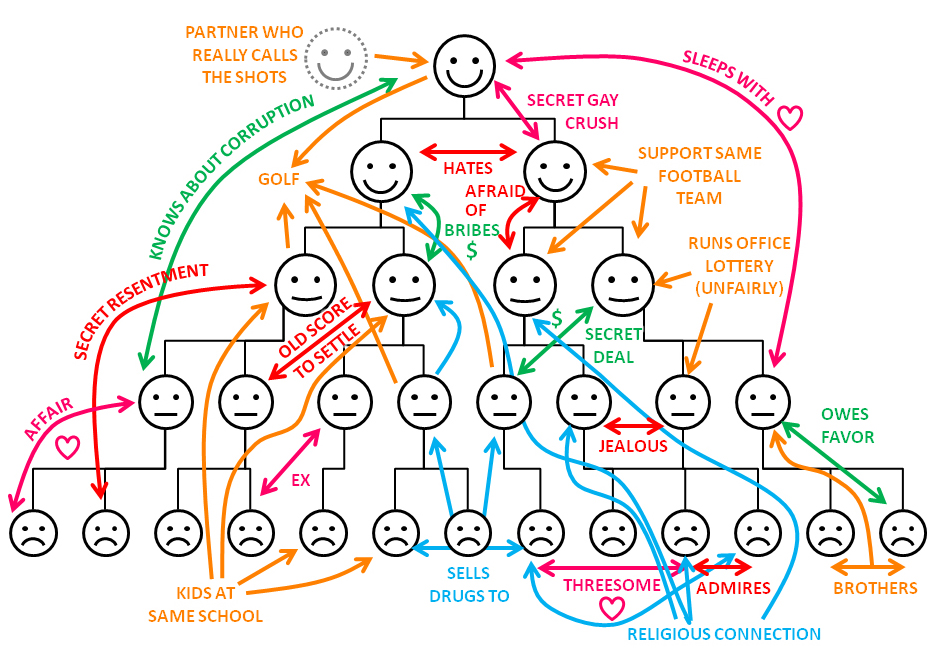
Sesuatu seperti itu .

Di sini, agar merasa nyaman di bidang penelitian yang serupa dengan yang dijelaskan, ada baiknya menggali granit sains. Benar, penggalian akan terjadi secara intensif - teori grafik sedang aktif dikembangkan. Itulah sebabnya ini adalah ujung tombak kemajuan - hanya sedikit orang yang merasa nyaman di sana.

Untuk memahami detail fungsi Decagon, kami akan bertamasya ke dalam sejarah.

Apa itu embedding grafik dan dari mana asalnya

Saya kebetulan mengamati perubahan dalam set metode canggih untuk memecahkan masalah memprediksi koneksi pada grafik selama empat tahun terakhir. Itu menyenangkan. Hampir seperti dalam dongeng - semakin jauh, semakin buruk. Evolusi mengikuti jalur dari heuristik yang menentukan lingkungan untuk bagian atas grafik ke kereta acak, kemudian metode spektral (analisis matriks) muncul, dan sekarang jaringan saraf.

Kami merumuskan masalah memprediksi hubungan:

Pertimbangkan grafik yang tidak diarahkan$$ $ inline $ \ begin {align *} G (V, E) \ end {align *} $ inline $ dimana
$$$ inline $ \ begin {align *} V \ end {align *} $ inline $ - banyak puncak$$ $ inline $ \ begin {align *} v \ end {align *} $ inline $ ,
$$$ inline $ \ begin {align *} E \ end {align *} $ inline $ - banyak tulang rusuk$$ $ inline $ \ begin {align *} e (u, v) \ end {align *} $ inline $ menghubungkan puncak$$ $ inline $ \ begin {align *} u \ end {align *} $ inline $ dan$$ $ inline $ \ begin {align *} v \ end {align *} $ inline $ .

Kami mendefinisikan set semua tepi yang mungkin$$ $ inline $ E ^ {\ diamond} $ inline $ kekuatannya
$$$ inline $ \ begin {align *} | E ^ {\ diamond} | & = \ frac {| V | * (| V | - 1)} {2} \\ \ end {align *} $ inline $ dimana
$$$ inline $ \ begin {align *} | V | = n \ end {align *} $ inline $ , Apakah jumlah simpul.

Jelas, banyak sisi yang tidak ada dapat dinyatakan sebagai$$ $ inline $ \ begin {align *} \ overline {E} = E ^ {\ diamond} - E \ end {align *} $ inline $ .

Kami menganggap itu di set$$ $ inline $ \ begin {align *} \ overline {E} \ end {align *} $ inline $ ada tautan yang terlewat, atau tautan yang akan muncul di masa mendatang, dan kami ingin menemukannya.

Solusinya turun ke mendefinisikan fungsi$$ $ inline $ \ begin {align *} D (u, v) \ end {align *} $ inline $ jarak antara simpul grafik, memungkinkan untuk struktur grafik$$ $ inline $ \ begin {align *} G (t_0, t_0 ^ \ star) \ end {align *} $ inline $ atur selama periode waktu tertentu$$ $ inline $ \ begin {align *} (t_0, t_0 ^ \ star) \ end {align *} $ inline $ memprediksi penampilan ujung-ujungnya$$ $ inline $ \ begin {align *} G (t_1, t_1 ^ \ star) \ end {align *} $ inline $ dalam jangkauan$$ $ inline $ \ begin {align *} (t_1, t_1 ^ \ star) \ end {align *} $ inline $ .

Salah satu publikasi pertama yang mengusulkan pindah dari pengelompokan ke tugas memprediksi hubungan dalam konteks mempelajari ekspresi gen bersama muncul dalam jurnal (seperti yang Anda duga) Bioinformatika pada tahun 2000. Sudah pada tahun 2003, sebuah artikel oleh John Kleinberg diterbitkan dengan tinjauan umum metode yang relevan untuk memecahkan masalah peramalan koneksi di jejaring sosial. Bukunya " Networks, Crowds, and Markets: Reasoning About a Connected World " adalah buku teks yang direkomendasikan untuk dibaca selama kursus cs224w, sebagian besar bab terdaftar di bagian bacaan wajib.

Sebuah artikel dapat dianggap sepotong pengetahuan di bidang sempit, seperti yang kita lihat, pada awalnya bermacam-macam metode kecil dan termasuk:

• Metode berdasarkan grafik tetangga - dan yang paling jelas adalah jumlah tetangga umum.

Kami memberikan definisi:

Atas$$ $ inline $ u $ inline $ adalah tetangga grafik untuk bagian atas$$ $ inline $ v $ inline $ jika iga$$ $ inline $ e (u, v) \ in E $ inline $ .

Kami menunjukkan$$ $ inline $ \ Gamma (u) $ inline $ banyak tetangga bertetangga$$ $ inline $ u $ inline $ ,

lalu jarak antar puncak$$ $ inline $ u $ inline $ dan$$ $ inline $ v $ inline $ dapat ditulis sebagai

$$$ inline $ D_ {CN} (u, v) = \ Gamma (u) \ cap \ Gamma (v) $ inline $ .

Secara intuitif, semakin besar persimpangan set tetangga dari dua puncak, semakin besar kemungkinan hubungan di antara mereka, misalnya, sebagian besar kenalan baru terjadi dengan teman teman.

Heuristik yang lebih maju - Koefisien Jacquard$$ $ inline $ D_J (u, v) = \ frac {\ Gamma (u) \ cap \ Gamma (v)} {\ Gamma (u) \ cup \ Gamma (v)} $ inline $ (yang sudah berusia seratus tahun) dan baru-baru ini (saat itu) jarak yang diusulkan Adamik / Adar$$ $ inline $ D_ {AA} (u, v) = \ sum_ {x \ in \ Gamma (u) \ cap \ Gamma (v)} \ frac {1} {\ log | \ Gamma (x) |} $ inline $ mengembangkan ide melalui transformasi sederhana.

• Metode berdasarkan jalur sepanjang grafik - idenya adalah bahwa jalur terpendek antara dua simpul pada grafik sesuai dengan peluang koneksi di antara mereka - semakin pendek jalur, semakin tinggi peluang. Anda dapat melangkah lebih jauh dan memperhitungkan tidak hanya jalur terpendek, tetapi juga semua jalur lain yang memungkinkan antara pasangan puncak, misalnya, menimbang jalur, seperti yang dilakukan oleh jarak Katz . Sudah lalu, panjang jalur yang diharapkan dari gelandangan acak disebutkan - cikal bakal metode rekomendasi teman Facebook.

Perkirakan kualitas perkiraan:

• Untuk setiap pasangan simpul$$ $ inline $ (u, v) $ inline $ setiap tulang rusuk yang tidak ada$$ $ inline $ e (u, v) \ in \ overline {E} $ inline $ hitung jaraknya$$ $ inline $ D (u, v) $ inline $ pada grafik$$ $ inline $ G (t_0, t_0 ^ \ bintang) $ inline $ .
• Sortir pasangan$$ $ inline $ (u, v) $ inline $ menurun jarak$$ $ inline $ D (u, v) $ inline $ .
• Bawa pergi$$ $ inline $ m $ inline $ pasangan dengan nilai tertinggi adalah perkiraan kami.
• Mari kita lihat berapa banyak tepi yang diprediksi muncul$$ $ inline $ G (t_1, t_1 ^ \ bintang) $ inline $ .

Penting untuk diingat bahwa jumlah tetangga umum dan jarak Adamik / Adar adalah metode yang kuat yang menentukan tingkat dasar kualitas perkiraan hanya untuk struktur tautan, dan jika sistem rekomendasi Anda menunjukkan hasil yang lebih lemah, maka ada sesuatu yang salah.

Secara umum, embedding grafik adalah cara untuk merepresentasikan grafik secara ringkas untuk tugas pembelajaran mesin menggunakan fungsi transformasi$$ $ inline $ \ begin {align *} \ phi: G (V, E) \ longmapsto \ mathbb {R} ^ d \ end {align *} $ inline $ .

Kami memeriksa beberapa fungsi ini, yang paling efektif dari yang pertama. Daftar yang lebih luas dijelaskan dalam sebuah artikel oleh Kleinberg. Seperti yang dapat kita lihat dari ulasan, bahkan kemudian mereka mulai menerapkan metode tingkat tinggi, seperti dekomposisi matriks, pengelompokan awal, dan alat-alat dari gudang linguistik komputasi. Lima belas tahun yang lalu, semuanya baru saja dimulai. Embeddings adalah satu dimensi.

Stroller acak berbentuk matriks

Tonggak berikutnya dalam perjalanan ke embeddings grafik yang sama adalah pengembangan metode berjalan acak. Untuk menemukan dan membenarkan formula baru untuk menghitung jarak, tampaknya, menjadi istirahat. Dalam beberapa aplikasi, tampaknya Anda hanya harus mengandalkan kesempatan dan mempercayai para gelandangan.

Kami memberikan definisi:

Matriks adjacency grafik$$ $ inline $ g $ inline $ dengan jumlah simpul yang terbatas$$ $ inline $ n $ inline $ (dinomori dari 1 hingga$$ $ inline $ n $ inline $ ) Apakah matriks persegi$$ $ inline $ a $ inline $ ukurannya$$ $ inline $ n \ kali n $ inline $ di mana nilai elemen$$ $ inline $ a_ {ij} $ inline $ sama dengan berat$$ $ inline $ w_ {ij} $ inline $ tulang rusuk$$ $ inline $ e (i, j) $ inline $ .

Catatan: di sini kami sengaja beralih dari indikator titik yang digunakan sebelumnya$$ $ inline $ u, v $ inline $ dan kami akan menggunakan notasi yang akrab dengan aljabar linier dan, secara umum, untuk bekerja dengan matriks$$ $ inline $ i, j $ inline $ .

Kami menggambarkan konsep yang dipertimbangkan:

Biarkan$$ $ inline $ g $ inline $ - grafik empat simpul$$ $ inline $ \ {A, B, C, D \} $ inline $ dihubungkan oleh tulang rusuk.

Untuk menyederhanakan konstruksi, kami mengasumsikan bahwa tepi grafik kami adalah dua arah, mis.$$ $ inline $ \ forall e (i, j) \ di E, \ ada e (j, i) \ di E \ land w_ {ij} = w_ {ji} $ inline $ .

$$$ sebaris $ e (A, B), w_ {AB} = 1; \\ e (B, C), w_ {BC} = 2; \\ e (A, C), w_ {AC} = 3; \ \ e (B, C), w_ {BC} = 1. $ inline $

Kami mewakili set tepi:$$ $ inline $ E $ inline $ - berwarna biru, dan$$ $ inline $ \ overline {E} $ inline $ - berwarna hijau.



$$$ inline $ \ begin {align *} A = \ kiri [\ begin {matrix} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 \\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {matrix} \ kanan] \ end {align *} $ inline $

Menulis grafik dalam bentuk matriks membuka kemungkinan menarik. Untuk mendemonstrasikannya, lihat karya Sergey Brin dan Larry Page, dan lihat bagaimana PageRank, sebuah algoritma untuk menentukan peringkat grafik, masih merupakan bagian penting dari pencarian Google.

PageRank - diciptakan untuk mencari halaman terbaik di Internet. Halaman dianggap baik jika dihargai (ditautkan) oleh halaman bagus lainnya. Semakin banyak halaman berisi tautan, dan semakin tinggi peringkatnya, semakin tinggi PageRank untuk suatu halaman.

Pertimbangkan interpretasi metode menggunakan rantai Markov .

Kami memberikan definisi:

Derajat simpul (derajat) adalah kekuatan banyak tetangga:
$$$d_i = |\Gamma(i)|$,

Ada di derajat dan keluar derajat. Sebagai contoh kita, mereka setara.

Kami membangun matriks adjacency tertimbang, dipandu oleh aturan:
$$$\begin{align*}M_{ij} = \left\{ \begin{matrix} \frac{1}{d_j} & \forall i,j \iff i \in \Gamma(j), \\ 0 & \forall i,j \iff i \notin \Gamma(j). \end{matrix} \right.\end{align*}$

$$$\begin{align*}M = \left[ \begin{matrix} 0 & \frac{1}{3} & \frac{1}{2} & 0 \\ \frac{1}{2} &0 & \frac{1}{2} & 1 \\ \frac{1}{2} & \frac{1}{3} & 0 & 0\\ 0 & \frac{1}{3} & 0& 0 \end{matrix} \right]\end{align*}$

, $$$M$1 (.. $$$M$— " "). $$$j$$$$i \in \Gamma(j)$.

$$$r_i$PageRank $$$i$, $$$d_i$. PageRank $$$j$bagaimana

$$

$$r_j = \sum_{i \to j}\frac{r_i}{d_i}$$

, $$$i$$$$j$PageRank, (.. PageRank), .

PageRank $$$\begin{align*}r = [r_1, r_2, ..., r_n]^T \end{align*}$— :

$$

$$r = Mr$$

-, ( ). $$$t$$$$i$$$$t+1$$$$j \in \Gamma(i)$, , — .

Kami menunjukkan $$$p(t)$, $$$i$pada waktu $$$t$. $$$p(t)$— , 1.

, $$$M_{ij}$— $$$j$$$$i$, $$$j$dan $$$p_j(t)$— , $$$j$$$$t$. , $$$i$

$\$\$display\$\$p\_i(t+1)\; =\; M\_\{i1\}p\_1(t)\; +\; M\_\{i2\}p\_2\; +\; .$. . + M_{in}p_n(t)$$display$$

,

$$

$$p(t + 1) = Mp(t)$$

- , $$$p(t + 1) = p(t)$, $$$p(t)$— . , PageRank $$$r = Mr$. — $$$r$PageRank — !

$$$r$PageRank . , $$$r^{(t0)} = [1/n, 1/n, ..., 1/n]^T$$$$r^{(t+1)} = Mr^{(t)}$$$$t$, , .. $$$||r^{(t+1)} - r^{(t)}||_1 < \epsilon$dimana $$$\epsilon$— . ( , $$$||x||_1 = \sum_{k} |x_k|$— $$$L_1$, ). $$$r^{(t+1)}$Page Rank . , 20-30 .

.

"" :

• .. " " — , — , PageRank . . .
• — — PageRank . - . $$$r$.

20 , !

- $$$\beta$, $$$1 - \beta$— . $$$1 - \beta \approx 0.15$, yaitu - 5-7 . — . PageRank :

$$

$$r_j = \sum_{i \to j}\beta\frac{r_i}{d_i} + (1-\beta)\frac{1}{n}$$

( , )

$$$M$,

$$

$$M^{\star} = \beta M + (1-\beta) [1/n]_{n×n}$$

. $$$r = M^{\star}r$. , , 37-38 14- cs224w 2017 , , Pinterest ( ).

. ?

:

• ;
• ;
• , .

PageRank. , , - , - .

— .

.

, . - ? 2006 .

:

, - $$$G$, - .

$$$i$$$$k$$$$f^{(i)} = [f_1, f_2, ..., f_k]^T$.



, $$$f_1$, , .

, , . - . , — (, ). , IT- , ( ) — .

, , — , , $$$A$dan $$$C$— .

, — .

- , Kaggle Hackerrank, , , (, ).

:

$$$S_k(x)$$$$x$$$$k$, $$$G$:

$$$\forall i \in V, i \in S_k(x) \iff f^{(i)}_{k} = x$

:

$$$\begin{align*}M^{p}_{ij} = \left\{ \begin{matrix} \beta M_{ij} + \frac{1-\beta}{|S_k(x)|} & \forall i,j \iff i \in S_k(x), \\ \beta M_{ij} & \forall i,j \iff i \notin S_k(x). \end{matrix} \right.\end{align*}$

$$$\begin{align*} r = M^{p} r \end{align*}$$$$\begin{align*} r \end{align*}$, . $$$\begin{align*} r \end{align*}$PageRank — . , $$$\begin{align*} r \end{align*}$— .

80% Pinterest.

, $$$\begin{align*}|S_k(x)| = 1\end{align*}$, yang disebut Random Walks with Restarts - kereta kembali dan kembali ke puncak minat kami. Sebagai hasilnya, kami mendapatkan ukuran kedekatan untuk setiap simpul grafik sehubungan dengan itu hanya satu. Dan ini memecahkan masalah memprediksi koneksi yang lebih baik daripada jarak Adamik / Adar memungkinkan.

Tambahkan lebih banyak peningkatan:

Ingatlah bahwa iga$$ $ inline $ \ begin {align *} e (i, j) \ in E \ in G \ end {align *} $ inline $ grafik kami memiliki bobot$$ $ inline $ \ begin {align *} w_ {ji} \ end {align *} $ inline $ .

Ini akan memungkinkan Anda untuk menentukan matriks tertimbang$$ $ inline $ \ begin {align *} M ^ w \ end {align *} $ inline $ probabilitas transisi:

$$$ inline $ \ begin {align *} M ^ {w} _ {ij} = \ left \ {\ begin {matrix} \ frac {w_ {ij}} {\ sum_ {j} w_ {ij}} & \ forall i, j \ iff e (i, j) \ di E, \\ 0 & \ forall i, j \ iff e (i, j) \ notin E. \ end {matrix} \ kanan. \ end {align *} $ inline $

Gelandangan akan membuat transisi, seperti sebelumnya, secara tidak sengaja, tetapi tidak lagi sama mungkin!

Pembaca yang penuh perhatian telah bertanya-tanya bagaimana cara mengukur bobot ini.

Facebook bingung dengan hal yang sama pada tahun 2011. Itu perlu untuk membangun sistem rekomendasi untuk teman-teman dari teman teman, sedemikian rupa sehingga memaksimalkan penciptaan koneksi baru. Dan langkah pertama adalah membuat grafik koneksi berbobot antara pengguna dari informasi di profil dan riwayat interaksi mereka (suka, pesan, foto bersama, dll.). Entah bagaimana mengukur kekuatan persahabatan di Internet.

$$$$ menampilkan $$ w_ {ij} = f ^ w (i, j) = e ^ {- \ sum_ {z} {\ xi_z x_ {ij} [z]}}, $$ menampilkan $$

dimana$$ $ inline $ \ begin {align *} x_ {ij} \ end {align *} $ inline $ Apakah vektor properti dari simpul dan tepi yang menghubungkannya, mis.$$ $ inline $ \ begin {align *} x_ {ij} = f ^ {(i)} \ cup f ^ {(j)} \ cup f ^ {e (ij)} \ end {align *} $ inline $ , dan$$ $ inline $ \ begin {align *} \ xi \ end {align *} $ inline $ Apakah vektor bobot harus dipelajari dari data.

Di sini, pembaca yang terlatih akan mengenali model linier , dan pembaca yang tidak siap akan memikirkan fakta bahwa perlu mengikuti kursus pembelajaran mesin terbuka untuk menghadapi gradient descent, yang dengannya kita akan mempelajari nilai-nilai bobot dalam vektor.$$ $ inline $ x_ {ij} $ inline $ - mereka akan menunjukkan bagaimana suka dan pesan mempengaruhi persahabatan di Internet.

Mengapa kita membutuhkan semua ini?

Selain fakta bahwa pendekatan yang dipertimbangkan memungkinkan kami untuk memprediksi koneksi dengan lebih baik, kita dapat mempelajari aturan untuk membangun tim yang sukses. Dan cari tahu apa yang harus dicari di masa depan.

Ingat kembali kondisi latihan kita. Kami mengamati perkembangan kerja sama (partisipasi bersama dalam kompetisi) dalam sekelompok datasaentists bersyarat dalam interval$$ $ inline $ \ begin {align *} (t_0, t_0 ^ \ star) \ end {align *} $ inline $ (misalnya, satu bulan kalender) dan kami ingin memprediksi pembangunan tim dalam interval$$ $ inline $ \ begin {align *} (t_1, t_1 ^ \ star) \ end {align *} $ inline $ (sebulan lagi). Selain berpartisipasi dalam kompetisi, kami melacak komunikasi di forum, suka kernel, dan apa lagi yang Anda suka. Semua informasi yang dikumpulkan disimpan dalam sebuah matriks$$ $ inline $ X ^ {\ star} \ in \ mathbb {R} ^ {(2k + l) \ kali | E |} $ inline $ (kolomnya adalah vektor$$ $ inline $ x_ {ij} $ inline $ ,$$ $ inline $ k, l $ inline $ - Dimensi vektor sifat simpul dan tepi$$ $ inline $ f ^ {(i)}, f ^ {e (ij)} $ inline $ , masing-masing) dan grafik$$ $ inline $ \ begin {align *} G \ end {align *} $ inline $ untuk dua interval waktu.

Mari kita siapkan data untuk pembelajaran mesin.

Untuk setiap titik$$ $ inline $ \ begin {align *} i \ end {align *} $ inline $ :

1) mendefinisikan banyak teman teman:

$$$$ menampilkan $$ \ Gamma ^ {fof} (i) = \ bigcup_ {j \ in \ Gamma (i)} \ Gamma (j) - \ Gamma (i) $$ menampilkan $$

2) dan membuat sub-grafik$$ $ inline $ \ begin {align *} G ^ {fof} (i) \ end {align *} $ inline $ koneksi dengan teman dan teman dari teman,$$ $ inline $ \ begin {align *} \ forall e (x, y) \ di E, e (x, y) \ dalam G ^ {fof} (i) \ iff x, y \ in \ Gamma ^ {fof} (i) \ cup \ Gamma (i) \ end {align *} $ inline $

3) pilih set simpul,$$ $ inline $ \ begin {align *} D_i: \ {d_1, ..., d_k \} \ end {align *} $ inline $ dengan siapa kami membentuk koneksi adalah contoh positif kami untuk belajar,

4) semua koneksi non-acak dari set$$ $ inline $ \ begin {align *} \ overline {D_i} = \ Gamma ^ {fof} (i) - D_i \ end {align *} $ inline $ - Ini adalah contoh negatif kami untuk pelatihan.

Tugas kita adalah memilih vektor bobot tersebut$$ $ inline $ \ begin {align *} \ xi \ end {align *} $ inline $ di mana contoh-contoh positif dari set$$ $ inline $ \ begin {align *} D_i \ end {align *} $ inline $ akan mendapatkan nilai PageRank Pribadi yang lebih tinggi dibandingkan dengan$$ $ inline $ \ begin {align *} i \ end {align *} $ inline $ dari contoh negatif.

Untuk melakukan ini, kami mendefinisikan fungsi kerugian, yang kami akan meminimalkan:

$$$$ menampilkan $$ L = \ sum_ {i} \ sum_ {d \ dalam D_i, \ overline {d} \ in \ overline {D_i}} h (r _ {\ overline {d}} - r_ {d}) + \ lambda || \ xi || ^ 2, $$ menampilkan $$

dimana$$ $ inline $ h (x) = 0 \ iff x <0; h (x) = x ^ 2 \ iff x \ geqslant 0; $ inline $ - hukuman karena melanggar ketentuan,$$ $ inline $ \ lambda $ inline $ - kekuatan$$ $ inline $ L_2 $ inline $ regularisasi bobot$$ $ inline $ \ xi $ inline $ ,$$ $ inline $ r $ inline $ Merupakan vektor dengan solusi persamaan$$ $ inline $ r = M ^ wr $ inline $ tentang$$ $ inline $ r $ inline $ untuk sub-grafik teman-teman dari satu teman$$ $ inline $ i $ inline $ .

Detail lucu - gradien fungsi ini dihitung dengan cara yang sama seperti PageRank, dengan metode daya. Detailnya ada di kuliah ke 17 edisi 2014, slide 9-27.

Ini adalah bagaimana ujung tombak kemajuan terlihat pada saat kenalan pertama saya dengan kursus cs224w.

Jalur kereta dorong acak dan atas dalam vektor

Dan kemudian datanglah kemenangan kemalasan!

Diketahui bahwa teori grafik ditemukan oleh Leonard Euler ketika dia bosan menyelesaikan masalah yang tidak terpecahkan tentang jembatan yang sekarang ada di Kaliningrad. Alih-alih mengeringkan kepalanya dengan sia-sia, ia menemukan alat matematika yang memungkinkannya untuk membuktikan ketidakmungkinan mendasar memecahkan teka-teki.

Dalam tradisi terbaik dari ilmu komputasi, kita juga akan malas dan bertanya pada diri sendiri tugas menemukan fungsi yang akan memungkinkan kita untuk menjauh dari representasi satu dimensi node dan pergi ke vektor properti multidimensi.

Di sini kita berkenalan dengan embeddings grafik dalam arti modern dari istilah tersebut.

Secara resmi, kami ingin:

1) Tentukan encoder (fungsi kesesuaian ENC yang mendefinisikan transformasi node$$ $ inline $ u $ inline $ dalam vektor$$ $ inline $ z_u $ inline $ );
2) Tentukan fungsi kesamaan node (ukuran kedekatan dalam grafik, yang akan kita terapkan pada input encoder);
3) Optimalkan parameter encoder sehingga:

$$$$ menampilkan $$ kesamaan (u, v) \ kira-kira z_ {v} ^ {T} z_v $$ menampilkan $$

Kami berusaha keras untuk memastikan bahwa simpul yang berjarak dekat pada grafik menerima representasi yang dekat dalam pemetaan vektor. Dengan kata lain, agar sudut antara kedua vektor yang diperoleh adalah minimal.

Hebat, tapi bagaimana cara menentukannya, kedekatan ini dalam grafik?

Sebagai contoh, kami mengasumsikan bahwa berat tulang rusuk adalah ukuran kedekatan yang baik dan dapat dianggap sama dengan produk skalar untuk hiasan dua simpul. Fungsi kerugian untuk kasus ini akan berbentuk:

$$$$ menampilkan $$ L = \ jumlah _ {(u, v) \ dalam V \ kali V} || z_ {u} ^ {T} z_v - A_ {u, v} || ^ 2, $$ menampilkan $$

masih menemukan (misalnya, gradient descent) matriks$$ $ inline $ Z \ in \ mathbb {R} ^ {d \ kali | V |} $ inline $ yang meminimalkan$$ $ inline $ L $ inline $ .

Pendekatan alternatif adalah menentukan lingkungan.$$ $ inline $ N (v) $ inline $ untuk KTT lebih luas dari banyak tetangga.

Ini akan membantu kami berjalan di sekitar grafik. Proyek pertama yang menggunakan pendekatan ini adalah DeepWalk . Inti dari metode ini adalah kita akan memulai gelandangan untuk berjalan di sekitar grafik secara acak dari setiap titik$$ $ inline $ v $ inline $ , dan beri urutan pendek dengan panjang tetap yang dikunjungi selama perjalanannya di word2vec.

Intuisi di sini adalah bahwa distribusi probabilitas mengunjungi titik-titik grafik - hukum kekuatan - sangat mirip dengan distribusi probabilitas kemunculan kata-kata dalam bahasa manusia. Dan karena word2vec berfungsi untuk kata-kata, maka untuk grafik dapat. Kami mencobanya - itu berhasil!

Dalam DeepWalk, seorang gelandangan mengimplementasikan proses Markov orde pertama - dari setiap titik yang kita tuju ke tetangga, sesuai dengan probabilitas dari matriks adjacency tertimbang$$ $ inline $ M $ inline $ (atau turunannya, seperti$$ $ inline $ M ^ w $ inline $ ) Di mana kami sampai di puncak tidak mempengaruhi pilihan langkah selanjutnya.

Untuk mengimplementasikan walk, Anda membutuhkan generator angka pseudo-acak dan sedikit aljabar . Saatnya menggunakan blok untuk kutipan untuk tujuan yang dimaksud.

“Siapa pun yang setuju dengan metode aritmatika generasi, tentu saja, adalah berdosa. Seperti yang telah berulang kali ditunjukkan, tidak ada angka acak - hanya ada metode untuk membuat angka seperti itu, dan prosedur aritmatika yang ketat, tentu saja, bukan metode seperti itu ... Kami hanya berurusan dengan resep untuk membuat angka ... "

- John von Neumann

Tetap memberi saran kepada mereka yang berjuang untuk kehidupan yang saleh untuk menemukan album "Black and White Noise" untuk dijual - pada tahun 1995 George Marsaglia menulis dalam CD sebuah array byte yang diterima dengan mendigitalkan suara dari amplifier selama memainkan artis rap dan menamainya sesuai.

Pengembangan metode ini adalah node2vec , di mana proses Markov orde kedua diimplementasikan - kita melihat dari mana asalnya, dan ini mempengaruhi kemungkinan memilih arah langkah selanjutnya. Mari kita lihat cara kerjanya.

Katakanlah kita mulai gelandangan berjalan di sekitar grafik dari atas$$ $ inline $ u $ inline $ berdekatan dengan bagian atas$$ $ inline $ s_1 $ inline $ puncak$$ $ inline $ s_2 $ inline $ dan$$ $ inline $ w $ inline $ - dalam dua langkah, dan$$ $ inline $ s_3 $ inline $ - dalam tiga. Setelah setiap langkah, kami dapat melakukan salah satu dari tiga tindakan yang mungkin: 1) kembali lebih dekat ke$$ $ inline $ u $ inline $ ; 2) jelajahi puncak pada jarak yang sama dari$$ $ inline $ u $ inline $ , seperti di mana kita berada sekarang; 3) menjauh dari$$ $ inline $ u $ inline $ .

Strategi ini diimplementasikan menggunakan dua parameter:
$$$ inline $ p $ inline $ - mengatur probabilitas untuk kembali ke simpul sebelumnya;
$$$ inline $ q $ inline $ - mengatur keseimbangan antara pencarian dalam luas dan pencarian secara mendalam.

Parameter ini menentukan probabilitas transisi yang tidak dinormalisasi sebagai berikut:

Katakanlah kita berada di puncak$$ $ inline $ w $ inline $ dan masuk ke dalamnya dari atas$$ $ inline $ s_1 $ inline $ . Untuk iga$$ $ inline $ e (w, s_1) $ inline $ kami akan menetapkan bobot (probabilitas tidak dinormalkan)$$ $ inline $ 1 / p $ inline $ . Untuk iga$$ $ inline $ e (w, s_2) $ inline $ -$$ $ inline $ 1 $ inline $ (Adapun semua tepi lainnya yang mengarah ke simpul sama dari$$ $ inline $ u $ inline $ ) Untuk pergi dari$$ $ inline $ u $ inline $ tulang rusuk$$ $ inline $ e (w, s_3) $ inline $ -$$ $ inline $ 1 / q $ inline $ .

Kemudian kita menormalkan probabilitas (sehingga jumlahnya sama dengan 1), dan mengambil langkah berikutnya.

Kami tertarik dengan urutan puncak yang dikunjungi - kami akan mengirimkannya ke word2vec ( artikel ini akan membantu Anda menghadapinya, atau kuliah 8 dari kursus Deep Learning dengan jari ). Pemilihan strategi untuk gelandangan, optimal untuk memecahkan masalah spesifik adalah bidang penelitian aktif. Misalnya, node2vec, yang kami ulas, adalah juara dalam klasifikasi puncak (misalnya, menentukan toksisitas obat, atau jenis kelamin / usia / ras anggota jaringan sosial).

Kami akan mengoptimalkan kemungkinan munculnya puncak di jalur gelandangan, fungsi kehilangan:

$$$$ display $$ L = \ sum_ {u \ in V} \ sum_ {v \ in N_ {R} (u)} -log (P (v | z_u)) $$ display $$

dalam bentuk eksplisitnya, beban komputasi yang agak mahal

$$$$ menampilkan $$ L = \ sum_ {u \ dalam V} \ sum_ {v \ dalam N_ {R} (u)} -log (\ frac {e ^ {z_ {u} ^ {T} z_v}} { \ sum_ {n \ dalam V} e ^ {z_ {u} ^ {T} z_n}}), $$ menampilkan $$

yang, kebetulan, diselesaikan dengan pengambilan sampel negatif , karena

$$$$ menampilkan $$ log (\ frac {e ^ {z_ {u} ^ {T} z_v}} {\ sum_ {n \ dalam V} e ^ {z_ {u} ^ {T} z_n}}) \ approx log (\ sigma (z_ {u} ^ {T} z_v)) - \ sum_ {i = 1} ^ {k} log (\ sigma (z_ {u} ^ {T} z_ {n_i})), \\ di mana \, \, \, n_i \ sim P_V, \ sigma (x) = \ frac {1} {1 + e ^ {- x}}. $$ menampilkan $$

Jadi, kami menemukan cara untuk mendapatkan representasi vektor dari simpul. Masalahnya adalah topinya!

Cara menyiapkan hiasan untuk tulang rusuk:

Kita perlu mendefinisikan operator yang memungkinkan untuk setiap simpul$$ $ inline $ u $ inline $ dan$$ $ inline $ v $ inline $ membangun representasi vektor$$ $ inline $ z _ {(u, v)} = g (z_u, z_v) $ inline $ , terlepas dari apakah mereka terhubung pada grafik. Operator semacam itu mungkin:

a) rata-rata aritmatika:$$ $ inline $ [z_u \ oplus z_v] _i = \ frac {z_u (i) + z_v (i)} {2} $ inline $ ;
b) karya Hadamard:$$ $ inline $ [z_u \ odot z_v] _i = z_u (i) * z_v (i) $ inline $ ;
c) norma L1 tertimbang:$$ $ inline $ || z_u - z_v || _ {\ overline {1} i} = | z_u (i) - z_v (i) | $ inline $ ;
d) tingkat L2 tertimbang:$$ $ inline $ || z_u - z_v || _ {\ overline {2} i} = | z_u (i) - z_v (i) | ^ 2 $ inline $ .

Dalam eksperimen, karya Hadamard berperilaku paling mantap.

Untuk jaga-jaga, ingat Teorema Makan Siang Gratis:

Tidak ada algoritma yang universal - ada baiknya memeriksa beberapa metode.

Pengembangan node2vec adalah proyek OhmNet , yang memungkinkan Anda untuk menggabungkan beberapa grafik ke dalam hierarki dan membangun simpul simpul untuk berbagai tingkatan hierarki. Awalnya dikembangkan untuk memodelkan ikatan antara protein dalam organ yang berbeda (dan mereka berperilaku berbeda tergantung pada lokasi).

Pembaca yang cerdik akan melihat kesamaan dengan struktur organisasi dan proses bisnis.

Dan kami - kami akan kembali ke contoh dari bidang perekrutan TI - pemilihan orang yang paling cocok untuk tim yang sudah ada. Sebelumnya, kami mempertimbangkan grafik unimodal dari hubungan-hubungan para datasaentists bersyarat yang diperoleh dari sejarah interaksi (dalam grafik unimodal dari vertex dan koneksi - dari jenis yang sama). Pada kenyataannya, jumlah lingkaran sosial di mana seorang individu dapat dimasukkan lebih dari satu.

Misalkan, selain sejarah partisipasi bersama dalam kompetisi, kami juga telah mengumpulkan informasi tentang bagaimana pusat data dikomunikasikan dalam obrolan nyaman kami. Sekarang kita sudah memiliki dua grafik koneksi, dan OhmNet sempurna untuk menyelesaikan masalah membuat embeddings dari beberapa struktur.

Sekarang - tentang kekurangan metode berdasarkan encoders dangkal - di dalam word2vec hanya ada satu lapisan tersembunyi, yang bobotnya menyandikan pengkodean. Pada output, kita mendapatkan tabel korespondensi vertex-vektor. Semua pendekatan tersebut memiliki batasan sebagai berikut:

• Setiap titik dikodekan oleh vektor unik dan model tidak menyiratkan berbagi parameter;
• Kami hanya dapat menyandikan simpul yang dilihat model selama pelatihan - kami tidak dapat melakukan apa pun untuk simpul baru (kecuali bagaimana melatih ulang pembuat sandi lagi);
• Vektor properti Vertex tidak diperhitungkan dengan cara apa pun.

Grafik jaringan convolutional bebas dari kekurangan yang ditunjukkan. Kita sampai ke Decagon!

Hari-hari kita adalah gelandangan acak untuk semua orang dan semua orang

Tentang gelandangan, saya beruntung bisa menulis gelar master pertama saya dan mempertahankannya kembali pada tahun 2003, tetapi dengan pelatihan mendalam saya harus menggunakan cara klasik untuk mencari tahu apa yang ada di bawah tenda. Dan itu lucu di sana.

Pertama, mari kita lihat mengapa metode standar pembelajaran mendalam - tidak sesuai dengan grafik.

Hitungan bukan kucing untuk Anda!

Perangkat modern pembelajaran mendalam (multilayer, konvolusional, dan jaringan berulang) dioptimalkan untuk memecahkan masalah pada sekuens dan kisi data yang cukup sederhana. Grafik adalah struktur yang lebih rumit. Salah satu masalah yang akan mencegah kita mengambil matriks kedekatan dan mengirimkannya ke jaringan saraf adalah isomorfisme .

Di kolom mainan kami$$ $ inline $ g $ inline $ terdiri dari simpul$$ $ inline $ \ {A, B, C, D \} $ inline $ , untuk membangun matriks kedekatan$$ $ inline $ a $ inline $ , kami menyarankan penomoran ujung-ke-ujung$$ $ inline $ \ {1,2,3,4 \} $ inline $ . Mudah untuk melihat bahwa kita dapat memberi nomor simpul secara berbeda, misalnya$$ $ inline $ \ {1,3,2,4 \} $ inline $ , atau$$ $ inline $ \ {4,1,3,2 \} $ inline $ - Setiap kali menerima matriks adjacency baru dari grafik yang sama.

$$$ inline $ \ begin {align *} A = \ kiri [\ begin {matrix} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 \\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {matrix} \ kanan], \, A ^ {\ {1,3,2,4 \}} = \ kiri [\ begin {matrix} 0 & 3 & 1 & 0 \\ 3 & 0 & 2 & 0 \\ 1 & 2 & 0 & 1 \\ 0 & 0 & 1 & 0 \ end {matrix} \ kanan], \, A ^ {\ {4,1,3,2 \}} = \ kiri [\ begin {matrix} 0 & 1 & 2 & 1 \\ 1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 3 \\ 1 & 0 & 3 & 0 \ end {matrix} \ kanan]. \ end {align *} $ inline $

Dalam hal segel, jaringan kami harus belajar mengenalinya untuk semua permutasi yang mungkin dari baris dan kolom - itu masalah lain. Sebagai latihan, cobalah mengubah penomoran titik-titik pada gambar di bawah ini sehingga ketika Anda menghubungkannya secara seri, Anda mendapatkan kucing.

Masalah berikutnya untuk grafik dengan jaringan saraf biasa adalah dimensi input standar. Ketika kami bekerja dengan gambar, kami selalu menormalkan ukuran gambar untuk mengirimnya ke input jaringan - itu adalah ukuran yang tetap. Grafik seperti itu tidak akan berfungsi dengan grafik - jumlah simpul dapat berubah-ubah - menekan matriks konektivitas ke dimensi tertentu tanpa kehilangan informasi adalah tantangan lain.

Solusi - kami akan membangun arsitektur baru, terinspirasi oleh struktur grafik.

Untuk melakukan ini, kami menggunakan strategi dua langkah sederhana:

1. Untuk setiap titik, kami membuat grafik komputasi menggunakan gelandangan;
2. Kami mengumpulkan dan mengubah informasi tentang tetangga.

Ingatlah bahwa kami menyimpan properti simpul dalam vektor$$ $ inline $ f ^ {(u)} $ inline $ - kolom matriks$$ $ inline $ X \ in \ mathbb {R} ^ {k \ kali | V |} $ inline $ dan tugas kami adalah untuk setiap titik$$ $ inline $ u $ inline $ mengumpulkan properti dari simpul tetangga$$ $ inline $ f ^ {(v \ in N (u))} $ inline $ untuk mendapatkan vektor embedding$$ $ inline $ z_ {u} $ inline $ . Grafik komputasi dapat memiliki kedalaman arbitrer. Pertimbangkan opsi dua lapis.

Lapisan nol adalah properti dari simpul, yang pertama adalah agregasi menengah menggunakan beberapa fungsi (ditunjukkan oleh tanda tanya), yang kedua adalah agregasi akhir, yang menghasilkan vektor yang menarik bagi kita.

Dan apa yang ada di dalam kotak?

Dalam kasus sederhana , lapisan neuron dan non-linearitas:

$$$$ menampilkan $$ h ^ 0_v = x_v (= f ^ {(v)}); \\ h ^ k_v = \ sigma (W_k \ sum_ {u \ dalam N (v)} \ frac {h ^ {k-1} _v} {| N (v) |} + B_k h ^ {k-1} _v), \ forall k \ in \ {1, ..., K \}; \\ z_v = h ^ K_v, $$ menampilkan $$

dimana$$ $ inline $ W_k $ inline $ dan$$ $ inline $ B_k $ inline $ - bobot model yang akan kita pelajari dengan gradient descent, menerapkan salah satu fungsi kerugian yang dipertimbangkan, dan$$ $ inline $ \ sigma $ inline $ - nonlinier, misalnya RELU:$$ $ inline $ \ sigma (x) = maks (0, x) $ inline $ .

Dan di sini kita menemukan diri kita di persimpangan - tergantung pada tugas yang dihadapi, kita dapat:

• untuk belajar tanpa seorang guru dan mengambil keuntungan dari salah satu fungsi kerugian yang dipertimbangkan sebelumnya - gelandangan, atau bobot ujung. Bobot yang dihasilkan akan dioptimalkan sehingga vektor dari simpul yang sama ditempatkan dengan kompak;
• mulai pelatihan dengan seorang guru, misalnya, untuk menyelesaikan masalah klasifikasi, bertanya-tanya apakah obat itu akan beracun.

Untuk masalah klasifikasi biner, fungsi kerugian mengambil bentuk:

$$$$ menampilkan $$ L = \ sum_ {v \ dalam V} y_v log (\ sigma (z_v ^ T \ theta)) + + (1-y_v) log (1- \ sigma (z_v ^ T \ theta)), $ $ display $$

dimana$$ $ inline $ y_v $ inline $ - kelas vertex$$ $ inline $ v $ inline $ ,$$ $ inline $ \ theta $ inline $ Apakah vektor bobot, dan$$ $ inline $ \ sigma $ inline $ - nonlinier, misalnya sigmoid:$$ $ inline $ \ sigma (x) = \ frac {1} {1 + e ^ {- x}} $ inline $ .

Di sini, pembaca yang terlatih akan mengenali lintas-entropi dan regresi logistik, sedangkan pembaca yang tidak siap akan berpikir tentang mengambil kursus pembelajaran mesin terbuka untuk merasa nyaman dengan tugas klasifikasi , sederhana , dan algoritma yang lebih maju untuk menyelesaikannya (termasuk peningkatan gradien ).

Dan kita akan melanjutkan dan mempertimbangkan bagaimana GraphSAGE , pertanda dari Decagon, bekerja.

Untuk setiap titik$$ $ inline $ v $ inline $ kami akan mengumpulkan informasi dari tetangga$$ $ inline $ u \ in N (v) $ inline $ , dan dirinya sendiri.

$$$$ menampilkan $$ h ^ k_v = \ sigma ([W_k \ cdot AGG (\ {h ^ {k-1} _u, \ forall u \ in N (v) \}), B_k h ^ {k-1} _v]), $$ menampilkan $$

dimana$$ $ inline $ AGG $ inline $ - penunjukan umum fungsi agregasi - yang paling penting - dapat dibedakan.

Rata-rata: ambil rata-rata tertimbang dari tetangga

$$$$ menampilkan $$ AGG = \ jumlah_ {u \ dalam N (v)} \ frac {h ^ {k-1} _u} {| N (v) |}. $$ menampilkan $$

Pooling: nilai rata-rata elemen-bijaksana / maksimum

$$$$ menampilkan $$ AGG = \ gamma (\ {Qh ^ {k-1} _u, \ forall u \ in N (v) \}). $$ menampilkan $$

LSTM: Kocok lingkungan (jangan campur!) Dan jalankan di LSTM

$$$$ menampilkan $$ AGG = LSTM ([h ^ {k-1} _u, \ forall u \ in \ pi (N (v))]). $$ menampilkan $$

Pinterest, , PinSAGE .

LSTM ( ). IT-.

:

• : , — , .
• , : / , — .

, — . , . , , , . (/) , , , — — , 30 .

.

— (multi-label node
classification task) — . — . () ( — — 42% ). GraphSAGE, , — .

!

, — , , . , .

- , Decagon. , -, -, , -, — ri . . - 964 ( ) .

— , -, -.

,

$$

$$h^k_v = \sigma(\sum_rW^{k-1}_r(\sum_{u \in N_r(v)} \frac{h^{k-1}_u}{\sqrt{|N_r(v)||N_r(u)|}}+\frac{h^{k-1}_v}{|N_r(v)|})),$$

dimana $$$\sigma$— , RELU. , Decagon — . , , GraphSAGE. , .

, .

— , . -. $$$(u,r,v)$, :

$$$\begin{align*}g(u,r,v) = \left\{ \begin{matrix} z^T_uD_{r_i}RD_{r_i}z_j & u,v - ; \\ z^T_uM_rz_v & u,v - \, \, , \,\, \, . \end{matrix} \right.\end{align*}$

, :

$$

$$p^{uv}_{r} = p((u,r,v) \in E) = \sigma (g(u, r, v)), \sigma(x) = \frac{1}{1 + e^{-x}}.$$

, (end-to-end) -, : (i) $$$W_r$— , (ii) $$$M_r$— - -, (iii) $$$R$— , (iv) $$$D_{r_i}$— .

— - .

— .

— , , : 1) — — ; 2) " , , , " — - . , , , .

— — .

, ( ) , . , , GenBank 1 , , - — , . — , - ( ) , SNAP .

.

Neo4j , (property graph).

, . , , — (i) -, (ii) , (iii) , — — . .

— :

Selain itu, kontribusi Neo4j untuk industri adalah untuk menciptakan bahasa Cypher deklaratif , yang mengimplementasikan model grafik dengan properti dan beroperasi dalam bentuk yang mirip dengan SQL dengan tipe data berikut: simpul, relasi, kamus, daftar, bilangan bulat, titik mengambang, dan angka biner, dan string. Contoh permintaan yang mengembalikan daftar film yang menampilkan Nicole Kidman:

MATCH (nicole:Actor {name: 'Nicole Kidman'})-[:ACTED_IN]->(movie:Movie) WHERE movie.year < $yearParameter RETURN movie 

Menggunakan kruk, Neo4j dapat dibuat bekerja di memori.

Penting juga menyebutkan Gephi - alat yang mudah digunakan untuk memvisualisasikan dan meletakkan grafik di pesawat - alat analisis jaringan pertama dari yang diuji secara pribadi. Dengan peregangan, kita dapat mengasumsikan bahwa dalam Gephi dimungkinkan untuk mengimplementasikan grafik dengan properti simpul dan tepi, meskipun bekerja dengannya tidak akan terlalu nyaman, dan serangkaian algoritma untuk analisis terbatas. Ini tidak mengurangi manfaat dari paket - bagi saya itu adalah yang pertama di antara alat visualisasi. Dengan menguasai format penyimpanan GEXF internal, Anda dapat membuat gambar yang mengesankan. Ini menarik kemampuan untuk dengan mudah mengekspor ke web, serta kemampuan untuk mengatur properti untuk simpul dan tepi waktu dan mendapatkan animasi yang rumit sebagai hasilnya - ia membangun rute untuk salesman dari data penjualan. Semua berkat tata letak grafik pada peta dengan koordinat simpul - bagian standar dari paket.

Sekarang saya melakukan sebagian besar penelitian secara analitis, saya menggambar di bagian akhir.

Pencarian saya untuk alat dan metode untuk memproses data dalam sistem yang terhubung dengan rumit terus berlanjut. Tiga tahun lalu saya menemukan solusi untuk bekerja dengan grafik multimodal. Perpustakaan SNAP Jure Leskovek adalah alat yang ia kembangkan untuk dirinya sendiri dan telah mengukur banyak hal. Saya menggunakan Snap.py - versi untuk Python (proksi ke fungsi SNAP diimplementasikan dalam C ++) dan satu set sekitar tiga ratus operasi yang tersedia sudah cukup bagi saya dalam banyak kasus.

Baru-baru ini, Marinka Zhitnik merilis MAMBO - seperangkat alat (di dalam - SNAP) untuk bekerja dengan jaringan multimoda dan tutorial dalam bentuk serangkaian notebook Jupyter dengan analisis contoh mutasi genetik.

Akhirnya, ada Grafik SAP HANA - ada di dalam ML, SQL, OpenCypher - semua yang diinginkan hati Anda.

Dalam mendukung SAP HANA, fakta bahwa penggalian cenderung menghasilkan data transaksi yang terstruktur dengan baik dari ERP, sedangkan data murni sangat berharga. Kelebihan lainnya - alat yang ampuh untuk menemukan sub-grafik dengan pola yang diberikan - tugas yang berguna dan sulit, implementasi yang dalam paket lain belum bertemu dan menggunakan program khusus . Lisensi gratis untuk pengembang menyediakan basis data 1 GB - cukup untuk bermain dengan jaringan yang cukup besar. Panggilan lucu - satu set algoritma analitik di luar kotak - kecil, PageRank perlu diimplementasikan secara independen. Untuk melakukan ini, Anda harus menguasai GraphScript , bahasa pemrograman baru, tetapi ini adalah hal- hal sepele . Seperti yang dikatakan pelatih slalom dayung saya, untuk tuan - itu debu!

Sekarang tentang di mana mendapatkan data untuk membuat grafik dari mereka. Beberapa ide:

• Repositori Publik Universitas: Stanford - General and Biomedical , Colorado ;
• Gabungkan rencana proyek dengan struktur organisasi dan daftar risiko;
• Identifikasi hubungan antara struktur produk, teknologi, dan keinginan pengguna;
• Melakukan studi sosiografi dalam sebuah tim;
• Datang dengan sesuatu dari Anda sendiri, terinspirasi oleh proyek kursus cs224w tahun lalu .

Apa yang harus ditakuti

Kita dapat mengatakan bahwa ini akan menjadi peringatan terakhir tentang risiko yang terkait dengan pihak ini.

Seperti yang Anda ketahui, saudara-saudara, tujuan program ini adalah untuk mencerminkan keadaan di garis depan kelompok riset yang sangat produktif dan murah hati. Ini seperti Leningrad , hanya tentang matematika modern. Kemungkinan efek samping:

1. Dunning-Krueger , dimodifikasi, tanpa euforia pemula dan dataran tinggi keunggulan. Leskovek mencoba mengejar ketinggalan.
2. Kebosanan di provinsi di tepi laut. Dari 400 orang dalam kursus yang diberikan peralatan, mereka membuat saya menulis sebuah proyek dan lulus ujian pada sesi pertama selama program master kedua saya, penghitungannya satu setengah. Para guru dalam kegiatan penelitian mereka tetap pada tingkat modularitas dan tindakan sentralitas. Pada mitaps tentang python dan data juga sedih. Secara umum, jika Anda tidak tahu bagaimana menghibur diri sendiri, saya memperingatkan Anda.
3. Kebanggaan dengan aksen Slavik dalam pidato bahasa Inggris.

Memutar memo

Hai, reproduksi!

Dalam petualangan yang Jura Leskovek berikan kepada kami, Anda perlu waktu luang. Kursus ini terdiri dari 20 kuliah, empat pekerjaan rumah, yang masing-masing direkomendasikan untuk mengalokasikan sekitar 20 jam, literatur yang direkomendasikan, serta daftar luas bahan tambahan yang akan memungkinkan untuk membuat kesan pertama tentang keadaan di garis depan kemajuan dalam topik apa pun yang dibahas.

Untuk menyelesaikan tugas, sangat disarankan untuk menggunakan pustaka SNAP (dalam arti tertentu, keseluruhan kursus dapat dianggap sebagai gambaran umum dari kemampuannya).

Selain itu, Anda dapat mencoba mengimplementasikan proyek Anda sendiri atau menulis tutorial tentang topik yang Anda sukai.

Saya pikir setelah terbenam dalam teori grafik, pertanyaan tentang pohon tidak lagi menakutkan. Namun, ini hanya pendapat seorang amatir yang tidak pernah dalam hidupnya melakukan wawancara dengan seorang pengembang.