👲🏾 ⏫ 🌦️ Pemrograman dinamis dalam masalah olimpiade ✊🏾 🛌🏾 👣

Hai

Baru-baru ini saya memecahkan masalah dari arsip Timus Online Judge dan menemukan bagian yang disebut tugas pemrograman dinamis . Jenis tugas ini sangat menarik bagi saya, karena seringkali pendekatan ini memastikan kecepatan dan keanggunan solusi. Apa itu pemrograman dinamis?

Pemrograman dinamis adalah pendekatan untuk memecahkan masalah di mana ada pembagian menjadi subtugas yang "lebih sederhana" dibandingkan dengan yang asli. Kata "dinamis" dekat artinya dengan "induktif": diasumsikan bahwa jawabannya dikenal untuk beberapa makna

k

$k$ , dan saya ingin menemukan jawabannya

k + 1

$k + 1$ . Dalam matematika, ini disebut transisi induktif, dan merupakan ide utama pemrograman dinamis.

Contoh sederhana

Tugas yang paling mencolok dan indikatif adalah tugas komputasi

n

$n$ jumlah urutan Fibonacci. Diketahui bahwa urutan memiliki sifat-sifat berikut:

F_{0} = F_{1} = 1, F_{n} = F_{n - 1} + F_{n - 2} .

$F_0 = F_1 = 1, \ F_n = F_ {n-1} + F_ {n-2}.$

Ini segera menyiratkan rumus pengulangan:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); }

Jika rekursi mencari angka "dari akhir", maka metode berikut secara berurutan menghitung semua angka yang terletak di antara

0

$0$ dan

n

$n$ :

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; }

Jelas bahwa untuk yang cukup besar

n

$n$ algoritma ini bekerja lebih cepat: tidak menghitung nilai antara beberapa kali. Pertimbangkan contoh yang sedikit lebih rumit.

Contoh 1. Anda berjalan di tangga tol. Untuk melangkah

i

$i$ langkah Anda harus membayar

a_{i}

$a_i$ koin. Anda dapat melangkah ke langkah berikutnya atau melompati satu langkah. Tugas: untuk lulus

n

$n$ langkah dan menghabiskan koin sesedikit mungkin.

Jelas bahwa melangkah di setiap langkah, kami meminimalkan jumlah "pembayaran", tetapi kami bisa mengalami langkah yang sangat mahal, yang ingin kami hindari. Buat array nilai

d

$d$ di mana pada

j

$j$ -tempat akan menjadi (minimum) jumlah koin yang harus dikeluarkan untuk sampai ke

j

$j$ langkah th. Segera jelas itu

d_{1} = a_{1}, d_{2} = a_{2}

$d_1 = a_1, \ d_2 = a_2$ . Dan kemudian kita akan mengambil minimal dua langkah sebelumnya dan menambahkan biaya langkah itu sendiri:

d_{i} = m i n k i r i (d_{i - 1}, d_{i - 2} k a n a n) + a_{i} .

$d_i = \ min \ kiri (d_ {i-1}, d_ {i-2} \ kanan) + a_ {i}.$

Kami sedikit mengubah kondisi masalah: misalkan pada beberapa langkah Anda bisa mendapatkan koin (ini artinya

a_{k} < 0

$a_k <0$ ) Apa yang perlu diubah dalam algoritma sehingga memberikan hasil yang benar?

Solusi

Kita hanya perlu mengubah "awal" dinamika kita. Jika tangga pertama tidak membawa kita koin, maka disarankan untuk melompatinya, jika

a_{1} < 0

$a_1 <0$ , lebih baik untuk melangkah dan mengumpulkan koin Anda. Jadi

d_{2} = m n t k i r i (0, d_{1} k a n a n) + a_{2}

$d_2 = \ mnt \ kiri (0, d_1 \ kanan) + a_2$ .

Pertimbangkan contoh lain yang menggunakan dinamika "dua dimensi".

Contoh 2. Di labirin ada

n k a l i m

$n \ kali m$ kamar, yang masing-masing berisi emas (dalam sangkar

(i, j)

$(i, j)$ kebohongan

a_{i j}

$a_ {ij}$ emas). Tugasnya adalah menentukan jumlah maksimum emas yang dapat dikumpulkan dengan rute optimal dari suatu titik

(0, 0)

$(0,0)$ to the point

(n, m)

$(n, m)$ jika Anda bisa turun atau ke kanan.

Jadi, kami ingin tahu rute terbaik ke sel

(i, j)

$(i, j)$ . Kita bisa sampai di sini dari dua sel -

(i - 1, j)

$(i-1, j)$ dan

(i, j - 1)

$(i, j-1)$ . Mengingat bahwa rute optimal untuk dua sel ini diketahui (mereka disimpan dalam beberapa tabel

d

$d$ ), lalu jawaban untuk sel

(i, j)

$(i, j)$ diperoleh sebagai berikut:

d_{i j} = m a x k i r i (d_{i - 1 j}, d_{i j - 1} k a n a n) + a_{i j} .

$d_ {ij} = \ max \ kiri (d_ {i-1j}, d_ {ij-1} \ kanan) + a_ {ij}.$

Ini adalah tugas pemrograman dinamis klasik lainnya, modifikasi yang cukup umum dalam tugas pemrograman olahraga. Tugas serupa dijelaskan secara lebih rinci di sini .

Tugas yang lebih menantang

Jika diinginkan, pendekatan dinamis dapat kacau di mana pun Anda inginkan. Pertimbangkan tugas dari arsip Hakim Timus Online.

Perumusan matematika dari masalah adalah sebagai berikut: diperlukan untuk menemukan jumlah minimum syarat yang diperlukan untuk menguraikan angka yang diberikan ke dalam kotak penuh.

Seperti sebelumnya, anggaplah kita tahu jawaban untuk semua angka

k - 1

$k-1$ yang disimpan dalam beberapa array

d

$d$ dan kami ingin menemukannya

d_{k}

$d_ {k}$ .

Ambil nomor ini

k

$k$ dan menganalisis situasi apa yang mungkin terjadi:

$k$ adalah kotak penuh. Dalam hal ini $d_ {k} = 1$ .
Mungkin nomor sebelumnya $k-1$ adalah kotak lengkap. Lalu $d_ {k} = d_ {k-1} + 1$ .

Secara umum, opsi untuk menambahkan unit ke unit sebelumnya tampaknya tidak terlalu buruk.

Kami melanjutkan sebagai berikut: kami mencari dekomposisi

k = q^{2} + s

$k = q ^ 2 + s$ sedemikian rupa

d_{q^{2}} + d_{s} < d_{k - 1} + 1.

$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$

Sejak

q^{2}

$q ^ 2$ - kotak penuh itu

d_{q^{2}} = 1

$d_ {q ^ 2} = 1$ , dan

d_{s} < d_{k - 1},

$d_s <d_ {k-1},$

yaitu, kami menemukan partisi yang lebih baik daripada

d_{k - 1} + 1

$d_ {k-1} + 1$ , dan jawabannya dalam kasus ini adalah

d_{k} = d_{s} + d_{q^{2}} = d_{s} + 1.

$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$

Contoh kode Java yang mengimplementasikan algoritma ini:

 for(int k = 1; k <= n; k++) { int best = d[k - 1] + 1; //      int q = 1; while(k - q*q >= 0) { // k = q*q + s if(k - q*q == 0) { // k -   best = 1; break; } else if(d[k - q*q] < best) best = d[k - q*q] + 1; q++; } d[k] = best; }

Pertimbangkan masalah berikut. Tujuannya adalah untuk membangun tangga dari

N

$N$ kubus sesuai aturan:

tangga memiliki setidaknya dua langkah;
tangga tidak dapat memiliki dua langkah yang identik;
langkah-langkah tangga berjalan dalam urutan menaik (yaitu, yang berikutnya lebih besar dari yang sebelumnya).

Kali ini kita akan membangun dinamika dua dimensi. Buat tabel

d

$d$ di mana posisinya

(i, j)

$(i, j)$ jumlah tangga yang terdiri dari

i

$i$ kubus yang tingginya tidak melebihi

j

$j$ . Jika berhasil, maka jawaban untuk masalah kita adalah jumlah

j u m l a h l i m i t_{j = 1}^{n} d_{n j} .

$\ jumlah \ limit_ {j = 1} ^ n d_ {nj}.$

Jadi, kita akan memecahkan masalah menemukan jumlah tangga yang terdiri dari

i

$i$ kubus yang tinggi

j

$j$ . Gambar menunjukkan tangga yang jatuh ke

d_{74}

$d_ {74}$ :

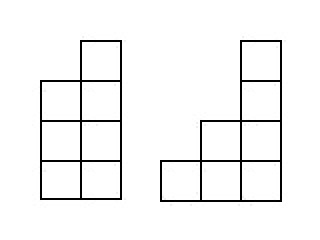
Karena kita tahu semua tangga, yang terdiri dari lebih sedikit kubus, kita akan “memisahkan” tangga

(i, j)

$(i, j)$ kolom kanan. Hasilnya adalah tangga c

i - j

$i-j$ kubus. Contoh untuk

i = 9, j = 4

$i = 9, \ j = 4$ :

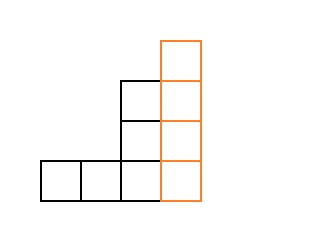
Tetapi untuk tangga seperti itu, hasilnya sudah diketahui, jadi kami akan memilah-milah semua tangga dengan siklus masuk

k

$k$ dan tambahkan semua hasil. Dengan cara ini

d_{i j} = j u m l a h l i m i t_{k = 1}^{j - 1} d_{i - j k} .

$d_ {ij} = \ jumlah \ limit_ {k = 1} ^ {j-1} d_ {i-jk}.$

Sekarang kita akan mengurutkan ketinggian tangga:

d_{i j} = j u m l a h l i m i t_{k = 1}^{j - 1} d_{i - j k}, j = o v e r l i n e 1, i .

$d_ {ij} = \ jumlah \ limit_ {k = 1} ^ {j-1} d_ {i-jk}, \ j = \ overline {1, i}.$

Akhirnya berubah

i

$i$ dari

1

$1$ sebelumnya

n

$n$ kami mendapatkan jawabannya.

Penting : dalam proses membangun matriks kita, perlu dipertimbangkan

d_{i i} = 1

$d_ {ii} = 1$ , karena kalau tidak beberapa jenis tangga akan "hilang" (ketika "memisahkan diri"), tetapi tidak perlu dikatakan bahwa tangga seperti itu tidak memenuhi kondisi masalah, jadi jawabannya adalah nomornya.

d_{n n} - 1

$d_ {nn} - 1$ .

Contoh kode Java yang mengimplementasikan algoritma ini:

 dp = new long[n + 1][n+1]; d[1][1] = 1; d[2][1] = 0; d[2][2] = 1; for(int i = 3; i < n + 1; i++) { for(int j = 2; j <i; j++) { long cnt = 0; for(int k = 1; k < j; k++) { cnt += d[i - j][k]; } d[i][j] = cnt; } d[i][i] = 1; //    } long answer = 0L; for(int i = 0; i <= n; i++) { answer += d[n][i]; } answer--; //

Tugas selanjutnya diselesaikan menggunakan array satu dimensi.

Jadi apa yang kita miliki. Ent pertama tahu 2 kata. Setiap ent mengajarkan semua kata yang dia tahu dirinya sendiri dua sen: muda dan tua. Pada gilirannya, kaum muda diajarkan sebanyak mungkin kata yang dia tahu, dan yang lama hanya diajarkan satu kata. Anda perlu tahu berapa banyak yang tahu persis

K

$K$ kata-kata (perlu untuk menyimpulkan jumlah modul ini

P

$P$ )

Solusinya cukup sederhana. Buat sebuah array

d

$d$ di mana pada

i

$i$ -tempat kita akan menyimpan jumlah en (modulo

P

$P$ ) siapa tahu

i

$i$ kata-kata. Itu semua dimulai dengan ent pertama, yang tahu dua kata, oleh karena itu

d_{2} = 1

$d_2 = 1$ . Dan kemudian semuanya sederhana:

Semua kata yang tahu jumlah kata ganjil sudah tua dan hanya bisa dipelajari dari kata-kata sebelumnya. Karena itu aneh $i: \ d_i = d_ {i-1};$
Adapun es yang tahu jumlah kata yang genap, ini adalah mereka yang menerima jumlah kata yang sama dari elf (muda) $+$ mereka yang telah belajar dari yang sebelumnya (lama); bahkan untuk $i$ kami punya $d_i = d _ {{i \ backslash 2}} + d_ {i-1}$ .

Masih berurusan dengan modulo perhitungan. Agar tidak menyimpan angka besar, kami akan segera mengingat semua nilai modulo.

Contoh kode Java yang mengimplementasikan algoritma ini:

 int[] d = new int[K + 1]; if(K >= 2) d[2] = 1; if(P != 1) { for(int i = 3; i <= K; i++) { if(i % 2 != 0) { d[i] = d[i - 1]; } else { d[i] = ((d[i/2] % P) + d[i - 1] % P) % P; } } } else d[K] = 0;

Sumber daya yang digunakan:

Hakim Online Timus;
Sedikit tentang pemrograman dinamis;
Modulo properti perbandingan.

Pemrograman dinamis dalam masalah olimpiade

Contoh sederhana

Tugas yang lebih menantang

More articles: