Geekly articles weekly

Metode numerik untuk menyelesaikan persamaan elips

Pendahuluan


Persamaan tipe elips yang paling umum adalah persamaan Poisson.
Banyak masalah fisika matematika direduksi menjadi solusi dari persamaan ini, misalnya, masalah distribusi suhu stasioner dalam masalah, difusi padat, masalah distribusi medan elektrostatik dalam media non-konduktor di hadapan muatan listrik, dan banyak lainnya.

Untuk menyelesaikan persamaan eliptik dalam kasus beberapa pengukuran, metode numerik digunakan untuk mengubah persamaan diferensial atau sistem mereka menjadi sistem persamaan aljabar. Keakuratan solusi ditentukan oleh langkah kisi koordinat, jumlah iterasi, dan kisi bit komputer [1]

Tujuan publikasi ini adalah untuk mendapatkan solusi persamaan Poisson untuk kondisi batas Dirichlet dan Neumann, untuk menyelidiki konvergensi metode relaksasi solusi menggunakan contoh.

Persamaan Poisson mengacu pada persamaan tipe elips dan dalam kasus satu dimensi memiliki bentuk [1]:

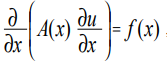
(1)

di mana x adalah koordinat; u (x) adalah fungsi yang diinginkan; A (x), f (x) adalah beberapa fungsi koordinat kontinu.

Kami memecahkan persamaan Poisson satu dimensi untuk kasus A = 1, yang dalam kasus ini berbentuk:

(2)

Pada interval [xmin, xmax] kita mendefinisikan grid koordinat seragam dengan langkah ::

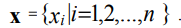
(3)

Kondisi batas jenis pertama (Kondisi Dirichlet) untuk masalah yang dipertimbangkan dapat direpresentasikan sebagai:

(4)

di mana x1, xn adalah koordinat titik batas wilayah [xmin, xmax]; g1, g2 - beberapa
konstanta.

Kondisi batas jenis kedua (kondisi Neumann) untuk masalah yang dipertimbangkan dapat direpresentasikan sebagai:

(5)

Mendiskritisasi kondisi batas Dirichlet pada kisi koordinat yang seragam (3) menggunakan metode beda hingga, kami memperoleh:

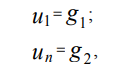
(6)

di mana u1, un adalah nilai fungsi u (x) pada titik x1, xn, masing-masing.

Mendiskritkan kondisi batas Neumann pada grid (3), kami memperoleh:

(7)

Persamaan diskritisasi (2) untuk titik-titik grid internal, kita memperoleh:

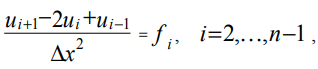
(8)

di mana ui, fi adalah nilai-nilai fungsi u (x), f (x) pada titik grid dengan koordinat xi.

Dengan demikian, sebagai hasil diskritisasi, kami memperoleh sistem persamaan aljabar linier dari dimensi n yang mengandung persamaan n - 2 dari bentuk (8) untuk titik internal wilayah dan persamaan (6) dan (7) untuk dua titik batas [1].

Berikut ini adalah daftar Python dari solusi numerik untuk persamaan (2) dengan kondisi batas (4) - (5) di grid (3).

Solusi Pencatatan
from numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0#    xn=5#    n=100#    dx=(xn-x0)/(n-1)#      dx x=[i*dx+x0 for i in arange(0,n,1)]#      dx def f(i):#    return 2*sin(x[i]**2)+cos(x[i]**2) v1=1.0#     (1 - , 2 - ) g1=0.0#     v2=2.0#'     (1 - , 2 - ) g2=-0.5#     a=zeros([n,n])#     nxn b=zeros([1,n])#  -     1 xn #     , #       #  v1, v2 b[0,n-1]=g1; if v1==1: a[0,0]=1 elif v1==2: a[0,0]=-1/dx a[0,1]=1/dx; else: print(' v1   ') b[0,n-1]=g2; if v2==1: a[n-1,n-1]=1 elif v2==2: a[n-1,n-1]=1/dx a[n-1,n-2]=-1/dx; else: print(' v2   ') #     , #     for i in arange(1, n-1,1): a[i,i]=-2/dx**2 a[i,i+1]=1/dx**2 a[i,i-1]=1/dx**2 b[0,i]=f(i) u=linalg.solve(a,bT).T#  def viz(v1,v2): if v1==v2==1: return "          " elif v1==1 and v2==2: return "          " elif v2==1 and v2==1: return "          " plt.figure() plt.title("     ") y=[f(i) for i in arange(0,n,1)] plt.plot(x,y) plt.grid(True) plt.xlabel('x') plt.ylabel('f(x)') plt.figure() plt.title("    ") plt.xlabel('x') plt.ylabel('u(x)') plt.plot(x,u[0,:],label='%s'%viz(v1,v2)) plt.legend(loc='best') plt.grid(True) plt.show()


Kami mendapatkan:









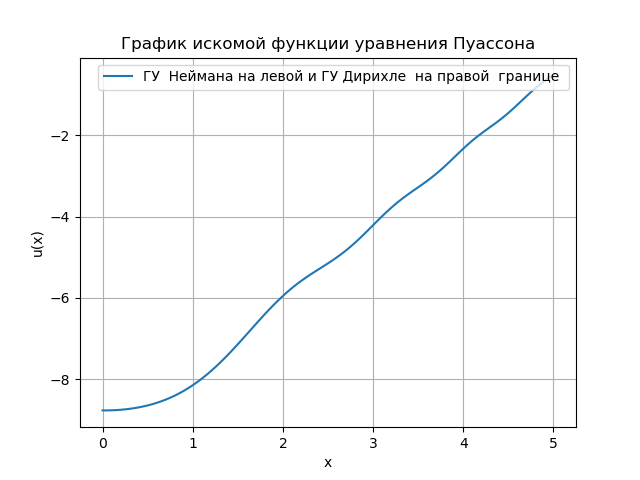
Program yang saya kembangkan dalam Python nyaman untuk menganalisis kondisi batas Algoritma solusi Python di atas menggunakan fungsi Numpy - u = linalg.solve (a, bT) .T untuk menyelesaikan sistem persamaan aljabar, yang meningkatkan kecepatan dengan matriks kuadrat {a}. Namun, dengan peningkatan jumlah pengukuran, perlu untuk beralih ke penggunaan tiga matriks diagonal, solusi yang rumit bahkan untuk tugas yang sangat sederhana, saya menemukan contoh di forum:

Contoh solusi dengan tiga matriks diagonal
 from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B) # solve A*x = B for x print('x \n', x) print('NUMPY time', time.clock()-ti, 'seconds')


Program solusi numerik pada seragam di setiap arah masalah Dirichlet grid untuk persamaan konveksi-difusi

[2]

(9)

Kami menggunakan pendekatan dengan perbedaan pusat untuk istilah konvektif dan metode relaksasi iteratif Untuk ketergantungan tingkat konvergensi pada parameter relaksasi untuk solusi numerik dari masalah dengan f (x) = 1 dan 6 (x) = 0,10. Dalam tugas grid:

(10)

Kami mewakili matriks A sebagai jumlah dari matriks segitiga diagonal, segitiga bawah dan atas:

(10)

Metode relaksasi sesuai dengan penggunaan metode iteratif :

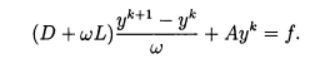
(11)

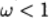
Di \ Bicara tentang relaksasi atas, kapan - tentang relaksasi yang lebih rendah.

Daftar Program
 from numpy import * """       -  . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2) #   - 10000 for k in arange(1, 10001,1): rn = 0. for j in arange(1,n2,1): for i in arange(1,n1,1): rr = - (y[i-1,j] - 2.*y [i, j] + y[i+1,j]) / h1**2 \ - (y[i,j-1] - 2.*y [i,j] + y[i,j+1]) / h2**2 \ + bb[i,j]*(y [i+1,j] - y [i-1,j]) / (2.*h1) - ff [i,j] rn = rn + rr**2 y[i,j] = y[i,j] - omega * rr / d rn = rn*h1*h2 if rn < tol**2: return y, k print ('   :') print (' 10000  =',sqrt(rn)) import matplotlib.pyplot as plt bcList = [0., 10.] sglist = ['-','--'] kk = 0 for bc in bcList: I1 = 1. I2 = 1. def f(x,y): return 1. def b(x,y): return bc n1 = 25 n2 = 25 m = 20 om = linspace(1., 1.95, m) it = zeros(([m])) for k in arange(0,m,1): omega = om[k] y, iter = relaxation(b, f, I1, I2, n1, n2, omega, tol=1.e-6) it[k] = iter s1= 'b =' + str(bc) sg = sglist[kk] kk = kk+1 plt.plot( om,it, sg, label = s1) plt.title("   \n     \n      $\\omega$") plt.xlabel('$\\omega$') plt.ylabel('iterations') plt.legend(loc=0) plt.grid(True) plt.show(
)

Kami mendapatkan:



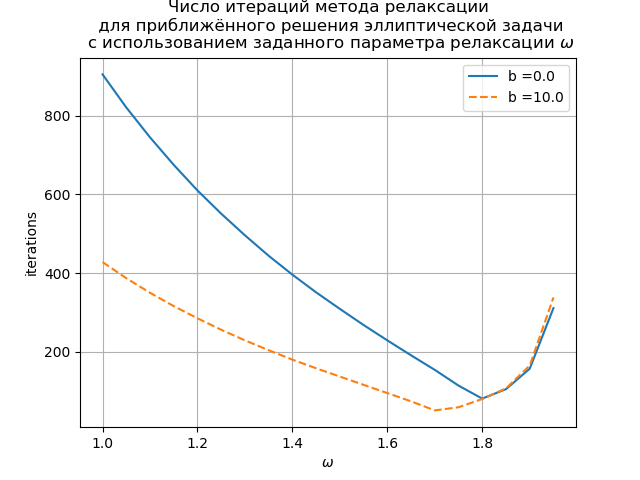
Grafik menunjukkan ketergantungan jumlah iterasi pada parameter relaksasi untuk persamaan Poisson (b (x) = 0) dan persamaan difusi konveksi (b (x) = 10). Untuk persamaan grid Poisson, nilai optimal dari parameter relaksasi ditemukan secara analitis, dan metode iteratif bertemu di .

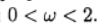
Kesimpulan:

  1. Solusi dari masalah elips di Python dengan sistem yang fleksibel untuk menetapkan kondisi batas
  2. Terlihat bahwa metode relaksasi memiliki rentang optimal ( 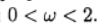) parameter relaksasi.

Referensi:

  1. Ryndin E.A. Metode untuk memecahkan masalah fisika matematika. - Taganrog:
    Rumah penerbitan TRTU, 2003 .-- 120 hal.
  2. Vabishchevich P.N. Metode Numerik: Workshop Komputasi. - M .: Rumah buku
    Librocom, 2010. - 320 hal.

Source: https://habr.com/ru/post/id418981/

More articles:


All Articles