Pemodelan permukaan air menggunakan prosesor FFT dan NeuroMatrix DSP

Transformasi Fourier cepat yang terkenal telah lama digunakan tidak hanya untuk memecahkan masalah pemrosesan sinyal digital, pengenalan objek dalam gambar, tetapi juga dalam grafik komputer. Jerry Tessendorf menggambarkan model matematika yang memungkinkan Anda untuk mensintesis gelombang laut dan menghidupkannya secara real time. Model ini didasarkan pada FFT dua dimensi.

Ketika saya ditugaskan mengembangkan aplikasi untuk prosesor DSP yang memvisualisasikan operasi FFT, saya menyadari bahwa pemodelan gelombang sangat cocok untuk tujuan ini.

Model matematika dari gelombang

Gagasan dasar model matematika gelombang dapat dijelaskan dengan ungkapan:
$$$\ mathbf H$ = FFT2D ( $$$\ mathbf {\ widetilde H}$ ), FFT2D dilambangkan sebagai operator FFT dua dimensi.

$$$\ mathbf H$ Apakah bidang ketinggian permukaan air (ukuran matriks $$$n_1 x n_2$ dimana $$$n_1$ dan $$$n_2$ dapat mengambil nilai kekuatan dua). Elemen dari matriks ini adalah ketinggian gelombang.

$$$\ mathbf {\ widetilde H}$ - sinyal (ukuran matriks $$$n_1 x n_2$ ), dihasilkan sesuai dengan hukum tertentu dan tergantung pada waktu.

$$$\ mathbf {\ widetilde H} = \ mathbf {\ widetilde H_0}. * \ mathbf A + \ overline {\ mathbf {\ widetilde H_0}}. * \ overline {\ mathbf A}$ dimana elemen-elemen dari matriks $$$\ mathbf A$ itu$$ $ inline $ e ^ {iω_ {ij} t} = cos⁡ (ω_ {ij} t) + isin (ω_ {ij} t) $ inline $ , dan matriks $$$\ overline {\ mathbf A}$ - konjugasi kompleks menjadi $$$\ mathbf A$ matriks $$$i = 0,1, ... n_1, j = 0,1, ... n_2$

$$$ω_ {ij}$ Merupakan elemen matriks $$$\ Besar {\ mathbf ω}$ .

$$$. *$ - perkalian matriks elemen-elemen.

$$$\ mathbf {\ widetilde H_0}$ - bidang ketinggian pada saat awal waktu t = 0.

$$$\ overline {\ mathbf {\ widetilde H_0}}$ - konjugasi kompleks menjadi $$$\ mathbf {\ widetilde H_0}$ matriks (ukuran $$$n_1 x n_2$ )

Untuk membuat animasi dari pergerakan gelombang secara real time, perlu untuk menghitung ulang matriks $$$\ mathbf {\ widetilde H}$ dan $$$\ mathbf H$ mengubah t . Matriks $$$\ mathbf {\ widetilde H_0}$ , $$$\ overline {\ mathbf {\ widetilde H_0}}$ dan $$$\ Besar {\ mathbf ω}$ dihitung sekali dan digunakan kembali.

Sekarang mari kita beralih ke deskripsi prosesor DSP, yang, berdasarkan pada rumus di atas, harus dapat:

1. Hitung FFT.
2. Gandakan elemen matriks dengan elemen.
3. Tambahkan matriks.
4. Hitung vektor sinus dan kosinus.

Sebagai prosesor DSP, 1879VM6Ya digunakan berdasarkan arsitektur NeuroMatrix, yang dikembangkan oleh Scientific and Technical Center "Module" CJSC. Rangkaian pada Gambar 1.

Prosesor ini mengandung 2 inti operasi paralel NMPU0 dan NMPU1 (beroperasi pada frekuensi 500 MHz), yang masing-masing memiliki prosesor RISC dan coprocessor vektor (NMCore FPU untuk floating point dan NMCore INT untuk aritmatika integer). Inti NMPU0 adalah untuk pemrosesan data floating-point, dan NMPU1 adalah untuk data integer. NMPU0 memiliki 8 bank SRAM internal (masing-masing 128 kB), dan NMPU1 memiliki 4 bank (128 kB) dengan memori yang sama. Pada 1879VM6Ya, pengontrol DMA dan antarmuka DDR2 diinstal.



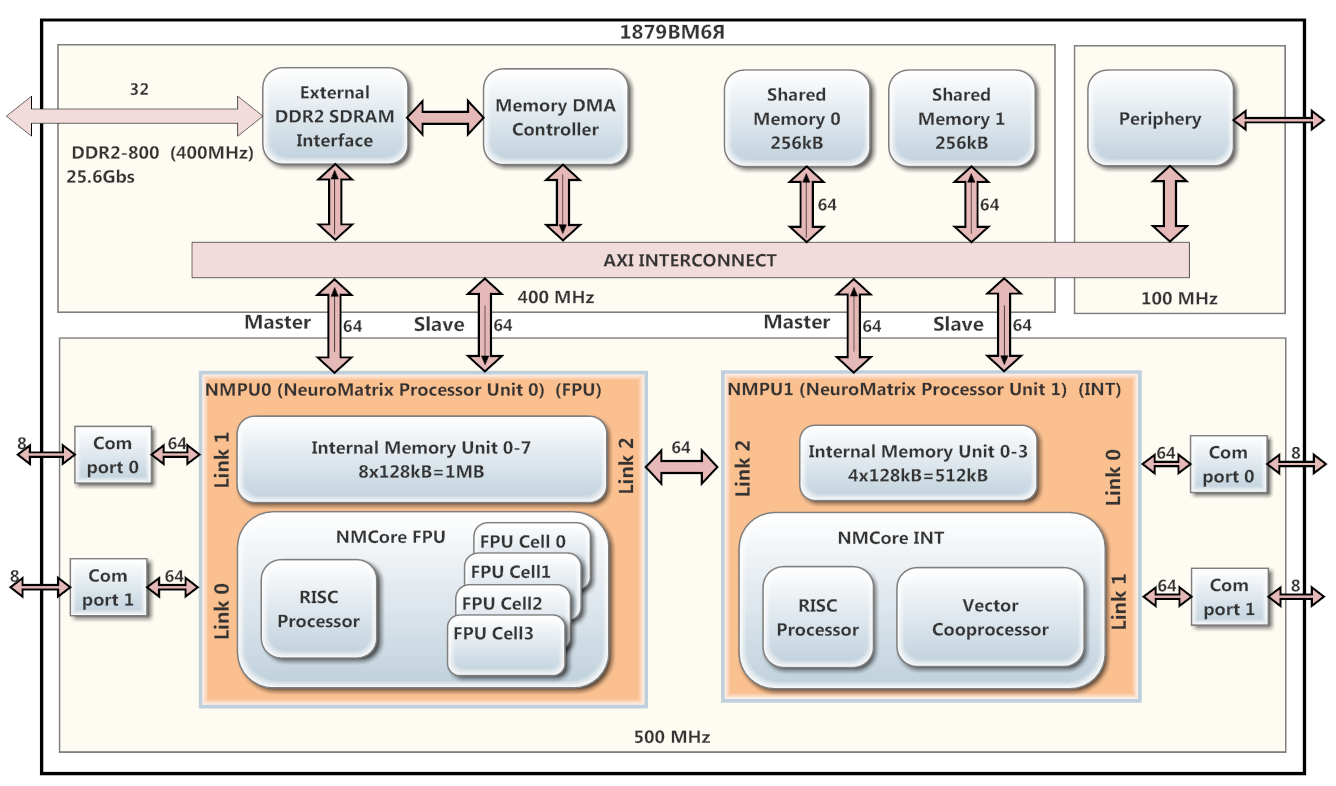Fig. 1. Diagram prosesor 1879VM6YA

Prosesor terletak pada modul instrumen MC121.01 (lihat. Gambar 2). Modul ini juga memiliki memori DDR2 512 MB.


Fig. 2. MS121.01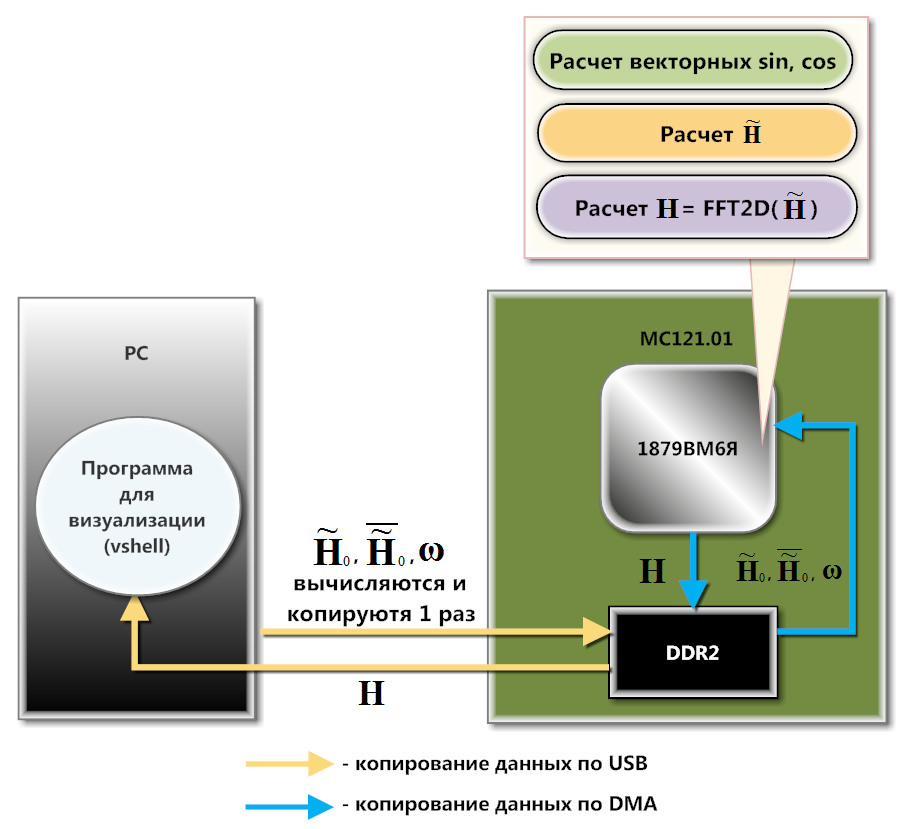



Fig. 3. Skema interaksi MC121.01 dan PC

MC121.01 berinteraksi dengan PC melalui USB (diagram pada Gambar 3). Pada tingkat perangkat lunak, interaksi ini diatur menggunakan perpustakaan pengunduhan dan pertukaran data, yang merupakan bagian dari SDK dewan ini. Matriks Precomputed $$$\ mathbf {\ widetilde H_0}$ , $$$\ overline {\ mathbf {\ widetilde H_0}}$ dan $$$\ Besar {\ mathbf ω}$ dimuat ke memori DDR2 melalui fungsi perpustakaan unduhan dan penukaran. Salinan pengontrol DMA $$$\ mathbf {\ widetilde H_0}$ , $$$\ overline {\ mathbf {\ widetilde H_0}}$ dan $$$\ Besar {\ mathbf ω}$ baris demi baris ke dalam memori internal (SRAM) prosesor. Mengunduh ke DDR2 disebabkan oleh fakta bahwa tidak satu pun dari matriks ini yang sepenuhnya cocok dengan SRAM. Penyalinan baris demi baris terjadi di sini, karena 1879BM6Ya menghitung dari SRAM lebih cepat daripada dari DDR2. Selain itu, bagian penting dari perhitungan dapat dilakukan dengan latar belakang DMA.

Menggunakan fungsi vektor dari perpustakaan NMPP untuk menghitung sinus, cosinus, perkalian dan penambahan vektor, prosesor menghitung baris matriks $$$\ mathbf {\ widetilde H}$ dan mengambil FFT satu dimensi dari mereka. Hasilnya dikirim oleh DMA kembali ke DDR2. Jadi dalam DDR2, sebuah matriks perantara terbentuk, dari kolom-kolom di mana prosesor menghitung FFT satu dimensi (setelah memuat kolom-matriks matriks perantara oleh DMA ke dalam SRAM). Dengan demikian, sebuah matriks terbentuk dalam DDR2 $$$\ mathbf H$ . Matriks ini diunduh ke PC untuk menggambar satu frame dengan gambar permukaan gelombang. Untuk menghidupkan gambar secara real time, Anda perlu menghitung matriks sesuai dengan algoritma yang dijelaskan di atas $$$\ mathbf H$ dengan meningkatkan parameter t .

Dalam prakteknya, ternyata 18796 menghitung matriks $$$\ mathbf H$ lebih cepat dari PC mengempiskannya. Karena itu, prosesor mungkin menganggur, menunggu PC untuk mengambil kumpulan data berikutnya. Dimungkinkan untuk menyelesaikan masalah ini menggunakan buffer cincin (berisi beberapa matriks $$$\ mathbf H$ ) diatur dalam papan memori DDR2.

Pada tingkat perangkat lunak, bekerja dengan pengontrol DMA dan buffer cincin dilakukan menggunakan fungsi pustaka HAL (Tingkat abstraksi Perangkat Keras) untuk prosesor NeuroMatrix.

Visualisasi permukaan gelombang

Saat DEM $$$\ mathbf H$ Dimuat ke dalam memori PC, Anda dapat memvisualisasikan permukaan. Untuk menampilkannya lebih jelas, Anda perlu mengoordinasikan x, y, z, menjelaskan titik-titik pada permukaan, dikalikan dengan matriks rotasi . Jadi kita mendapatkan koordinat baru dari permukaan x ', y', z ', memutarnya pada sudut tertentu.

Dengan menskalakan koordinat baru dan menghubungkan titik-titik di sepanjang mereka dengan garis lurus, Anda dapat melihat animasi gelombang laut (lihat video di bawah). Untuk visualisasi permukaan, perpustakaan digunakan untuk menampilkan gambar pada layar vshell.

Kesimpulan

Kesimpulannya, saya ingin mengatakan bahwa perhitungan dan transmisi melalui USB satu matriks $$$\ mathbf H$ dengan ukuran angka float 256x256, ~ 4,7 juta siklus clock dihabiskan (72 siklus clock per float). Frame rate ~ 107. Jika Anda tidak memperhitungkan waktu yang diperlukan untuk mentransfer data melalui USB, maka perhitungannya akan menelan biaya ~ 2,5 juta siklus (38 siklus per float). Ini adalah total waktu yang dihabiskan oleh prosesor 1879² pada multiplikasi elemen-bijaksana dan penambahan matriks, perhitungan FFT, sinus, cosinus, dan menyalin menggunakan DMA. Perhitungan ini dilakukan dengan latar belakang transfer data USB.

Perbedaan 2,2 juta siklus clock (4,7 juta - 2,5 juta = 2,2 juta) menunjukkan bahwa dalam sistem PC-MC121.01 USB adalah "bottleneck", dan 1879VM6YA dapat dimuat dengan perhitungan dengan 46% lebih banyak tanpa menerima FPS drawdown.

Saya juga ingin mencatat bahwa dengan latar belakang transfer data USB dan perhitungan pada coprocessor untuk floating point, coprocessor untuk integer aritmatika, yang tidak digunakan dalam tugas ini, dapat digunakan.

Tabel ini memperlihatkan kinerja beberapa fungsi vektor dari pustaka nmpp.

Fungsi	Bar
FFT satu dimensi, 256 poin	1770
Sine, 256 poin	1400
Cosine, 256 poin	1400

Referensi:

NMPP - perpustakaan primitif untuk arsitektur NeuroMatrix
HAL - perpustakaan abstraksi yang bergantung pada perangkat keras NeuroMatrix
VSHELL - pemrosesan gambar dan pustaka tampilan