Tugas dari buku teks sekolah I

Bagian I
Bagian II
Bagian III

Pertimbangkan solusi algoritmik untuk masalah nomor 38 dari buku "Tugas untuk anak-anak dari 5 hingga 15 tahun"

Hitung jumlahnya:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(dengan kesalahan tidak lebih dari 1% dari jawabannya)

Di bawah ini adalah algoritma untuk menghitung jumlah parsial dari seri ini dalam Skema (Lisp) di drRacket (drRacket memungkinkan Anda untuk melakukan perhitungan dalam fraksi biasa):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

Dua contoh terakhir drRacket dihitung dengan kesalahan



Program ini dapat dijalankan di ide online ideone.com dan codepad.org .



Jika kita mempertimbangkan jumlah parsial dalam fraksi biasa, kita dapat melihat bahwa jumlah seri adalah

$$

$$\ frac {n} {n + 1}$$

Biarkan saya mengingatkan Anda itu $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ di $$$n \ hingga \ infty$

Volume kedua dari Kursus Kalkulus Diferensial dan Integral 363 (4) mempertimbangkan kasus umum

$$

$$\ sum \ frac {1} {(\ alpha + n) (\ alpha + n +1)} = \ frac {1} {\ alpha + 1}$$

Tugas dari kursus "Matematika untuk Pengembang":
Temukan jumlah anggota secara berurutan $$$\ frac {2n-1} {4n + 5}$ berbaring di luar interval $$$(1- \ frac {1} {1000}; 1+ \ frac {1} {1000})$

Mari kita beralih ke topik utama artikel.

Mari kita pertimbangkan satu lagi contoh dari buku masalah.
43 . Bilangan kelinci (Fibonacci), membentuk urutan $$$(a_ {1} = 1), 1, 3, 5, 8, 13, 21, 34, ...,$ di mana $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ untuk semua orang $$$n = 1, 2, ...$ . Temukan pembagi angka terbesar $$$a_ {100}$ dan $$$a_ {99}$ .

Jawaban: Dua angka Fibonacci yang berdekatan adalah coprime, mis. $$$\ gcd (u_ {n + 1}, u_ {n}) = 1$
(gcd adalah pembagi umum terbesar, yaitu GCD).

"Bukti dari buku" Melampaui Halaman dari Buku Teks Matematika "[10-11]


Dalam tugas selanjutnya, Anda perlu menghitung rasio emas , $$$\ frac {\ sqrt {5} + 1} {2} \ sekitar 1.618$ . [Ini adalah rasio aspek kartu pos yang tetap sama saat memotong kotak yang sisi-sisinya adalah sisi yang lebih kecil dari kartu pos.]

53 . Untuk urutan angka Fibonacci $$$a_ {n}$ tugas 43 menemukan batas hubungan $$$\ frac {a_ {n + 1}} {a_ {n}}$ sambil berjuang $$$n$ hingga tak terbatas:

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2, \ frac {3} {2}, \ frac {5} {3}, \ frac {8} {5}, \ frac { 13} {8}, \ frac {21} {13}, \ frac {34} {21}.$$

Pertimbangkan segmen yang mewakili perbedaan dua anggota seri yang berdekatan $$$\ frac {a_ {n + 1}} {a_ {n}}$ .

Bahkan anggota seri $$$\ frac {a_ {n + 1}} {a_ {n}}$ mewakili urutan yang berkembang $$$x_ {n}$

$$

$$\ frac {3} {2}, \ frac {8} {5}, \ frac {21} {13}, ...,$$

Anggota baris ganjil $$$\ frac {a_ {n + 1}} {a_ {n}}$ mewakili urutan menurun $$$y_ {n}$

$$

$$2, \ frac {5} {3}, \ frac {13} {8}, ...,$$

Oleh lemma interval tertanam (Kursus kalkulus diferensial dan integral, 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

Untuk baris kita pada suatu titik $$$c$ kesetaraan yang adil $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

Membagi $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ pada $$$a_ {n + 1}$ kita mendapatkan persamaannya $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ .
Dengan mengganti $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x, \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ kita mendapatkan persamaan kuadratik $$$x = 1 + \ frac {1} {x}$ .

Jika dalam program geogebra kita menghubungkan titik 2 dan $$$\ frac {3} {2}$ , $$$\ frac {3} {2}$ dan $$$\ frac {5} {3}$ , $$$\ frac {5} {3}$ dan $$$\ frac {8} {5}$ dll. - dapatkan sosok yang mirip diri sendiri




Secara umum, ada algoritma standar untuk menghitung angka Fibonacci dalam Python.
Algoritma ini tersedia di Python.org

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

Anda dapat memeriksa tautannya
Ubah algoritma ini sehingga mencetak perkiraan dengan rasio emas. Untuk dua angka yang berdekatan a dan b, kami akan membagi jumlah a + b dengan b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

Anda dapat memeriksa tautannya

Berikut adalah beberapa tugas dari tutorial SICP mengenai rasio emas.


Contoh berikut dari buku tugas "Tugas untuk anak-anak dari 5 hingga 15 tahun"
54 . Hitung fraksi lanjutan tak hingga

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}}}$$

UPD Pertimbangkan persamaannya

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

Menurut Teorema 236 dan 235 dari buku "Teori Angka":

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

Kami menyusun tabel nilai $$$P_ {n}$ dan $$$Q_ {n}$ di $$$n = 0,1:$



jadi itu $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1}, 2 \ alpha ^ {2} - 2 \ alpha -1 = 0$

dan sejak itu $$$\ alpha> 0,$ lalu

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

Pertimbangkan masalah dari buku “Di balik halaman buku teks matematika” [10-11]
4 . Tunjukkan nomor itu $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ sama dengan jumlahnya $$$\ varphi$ mendefinisikan rasio emas.

Pertimbangkan pilihannya $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
Kursus kalkulus diferensial dan integral, 35 (2)

Dengan cara ini $$$x_ {n + 1}$ diperoleh dari $$$x_ {n}$ sesuai dengan formula

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... Dengan teorema utama, opsi $$$x_ {n}$ memiliki batas hingga $$$a$ . Untuk menentukannya, kami melewati batas kesetaraan

$$

$$x_ {n + 1} ^ {2} = c + x_ {n};$$

Kami mendapatkan sedemikian rupa sehingga $$$a$ memenuhi persamaan kuadrat

$$

$$a ^ {2} = c + a$$

Persamaan ini memiliki akar tanda yang berbeda; tetapi batas yang menarik bagi kita $$$a$ tidak boleh negatif, karena itu, sama dengan persis akar positif:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

Dari mana kita dapat menyimpulkan bahwa "rasio emas" adalah solusi untuk persamaan $$$a ^ {2} = c + a$
di $$$c = 1$ .


Selanjutnya, dalam Kursus Kalkulus Diferensial dan Integral, 35 (3), sebuah algoritma untuk menghitung angka terbalik dianggap

Biarkan $$$c$ Apakah ada angka positif, dan cantumkan $$$x_ {n} = cy_ {n}$ . Relasi rekursi yang tertulis di atas akan digantikan oleh:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

Mengambil nilai awal $$$y_ {0}$ dalam kondisi: $$$0 <y_ {0} <\ frac {1} {c}$ kita dapat itu $$$y_ {n}$ meningkat secara monoton, akan cenderung $$$\ frac {1} {c}$ . Menurut skema ini, pada mesin hitung, angka terbalik dihitung $$$c$ .

Algoritma perhitungan angka terbalik $$$c$ dalam Python:
( Ideone.com dan codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

Fungsi timbal-balik mengambil angka sebagai input $$$c$ nilai awal $$$y_ {0}$ , jumlah iterasi $$$n$ dan mengembalikan array "perkiraan" ke nomor tersebut $$$\ frac {1} {c}$ .
$$$y_ {0} = 0,1$ di $$$c <10$
$$$y_ {0} = 0,01$ di $$$10 <c <100$
$$$y_ {0} = 0,001$ di $$$100 <c <1000$
dll.
Contoh bagaimana fungsi resiprokal bekerja dengan beragam $$$c$

 >>> reciprocal(3,0.1,10) 

[0,1, 0,17, 0,2533, 0,31411733000000003, 0,3322255689810133, 0,3333296519077525,
0.3333333332926746, 0.3333333333333333337, 0.33333333333333337, 0.33333333333333337]

 >>> reciprocal(8,0.1,10) 

[0,1, 0,12, 0,1248, 0,12499968, 0,1249999999991808, 0,125, 0,125, 0,125, 0,125, 0,125, 0,125]

 >>> reciprocal(5,0.1,10) 

[0,1, 0,15000000000000002, 0,1875000000000000003, 0,19921875000000003, 0,19999694824218753, 0,1999999999534339, 0,2000000990000000004, 0,19999999999999998,
0,19999999999999998, 0,19999999999999998]

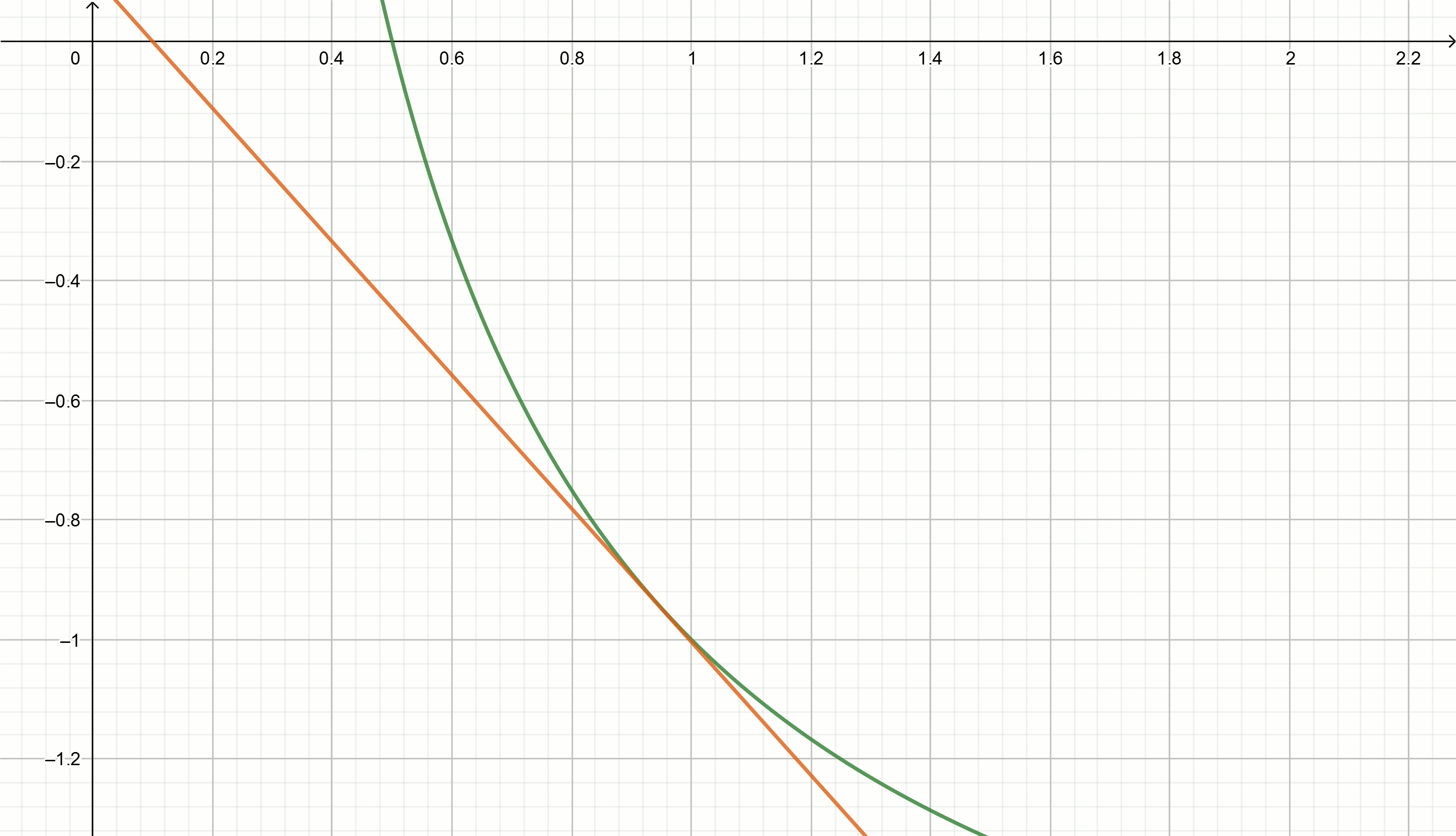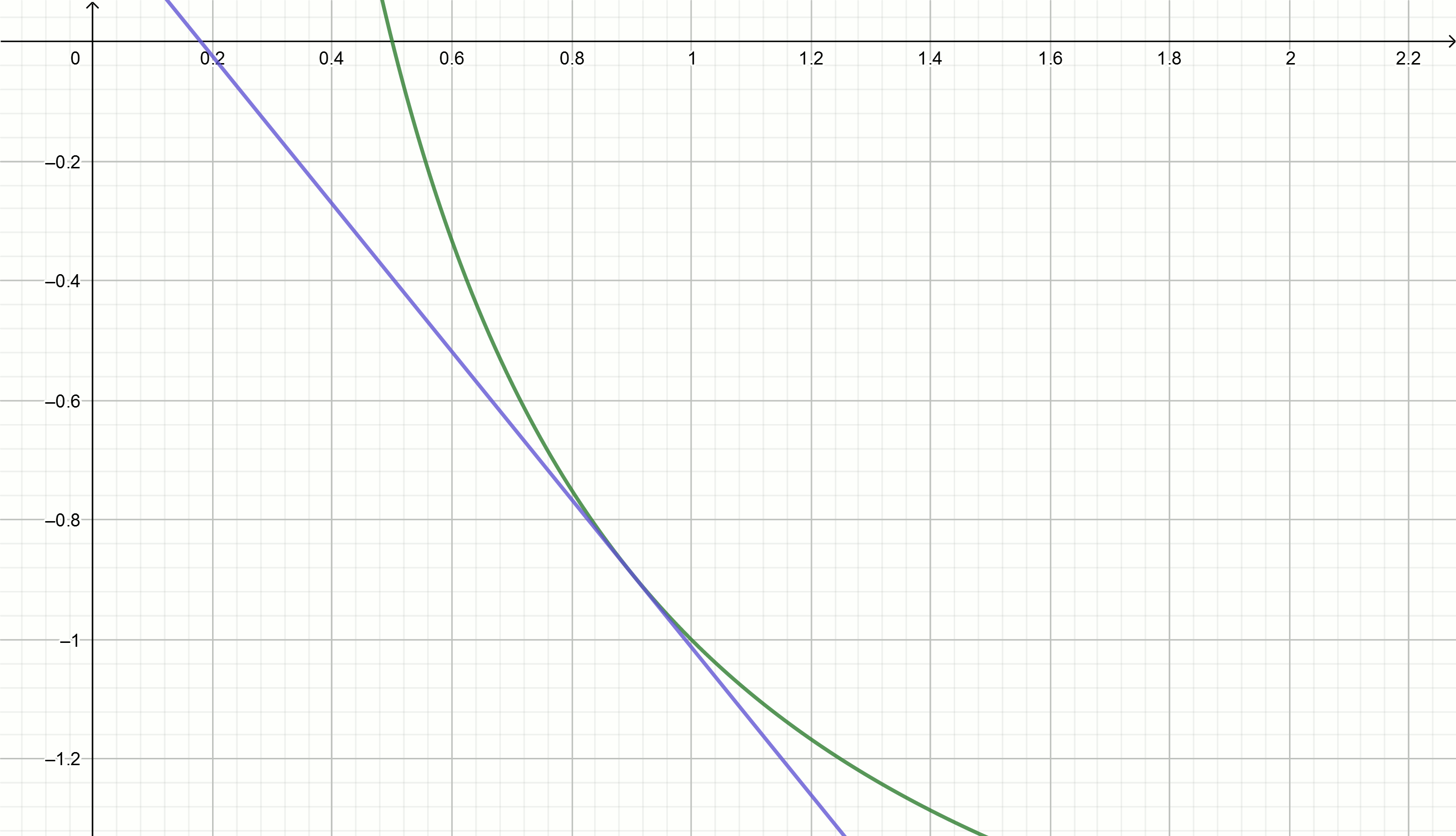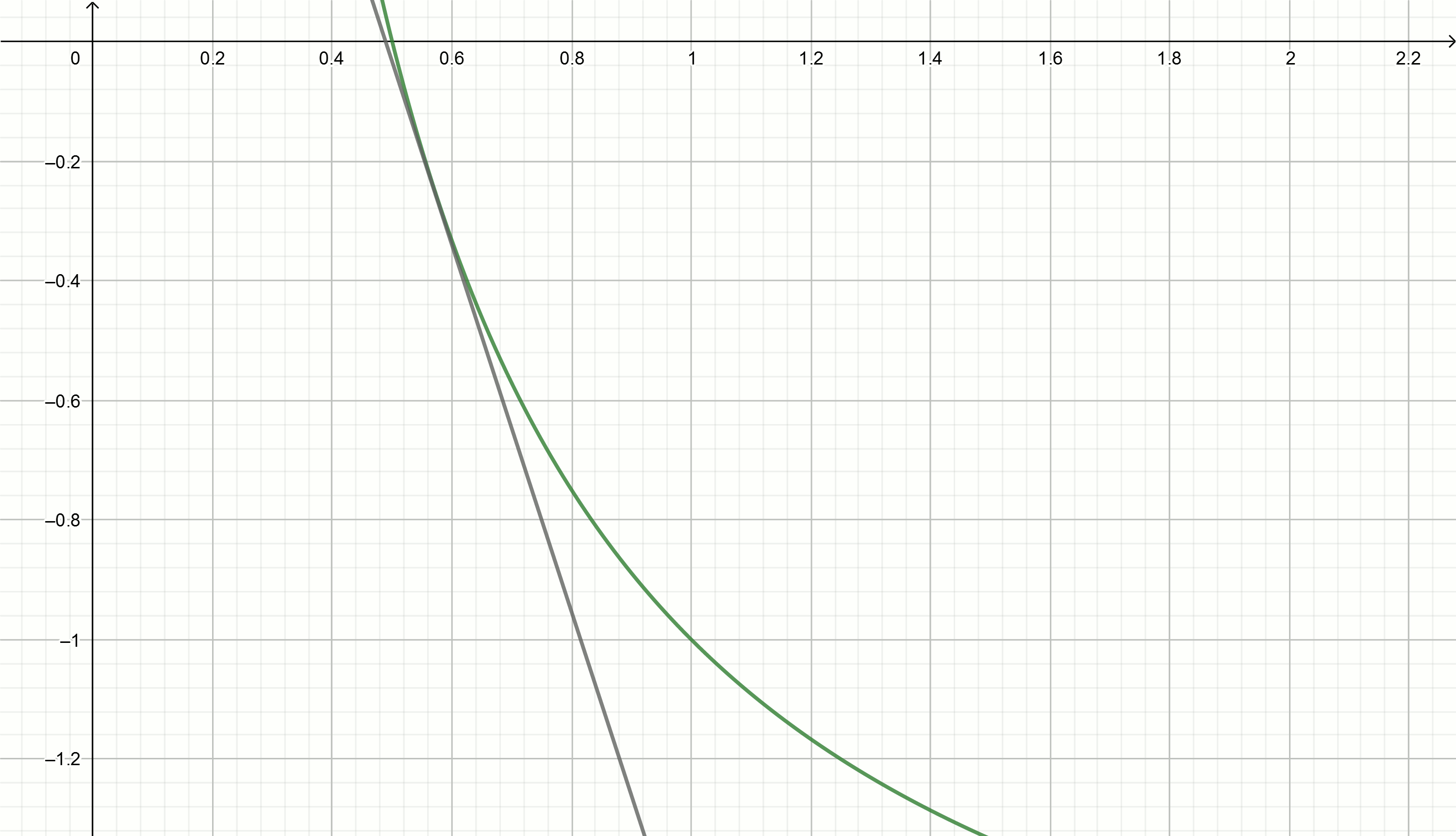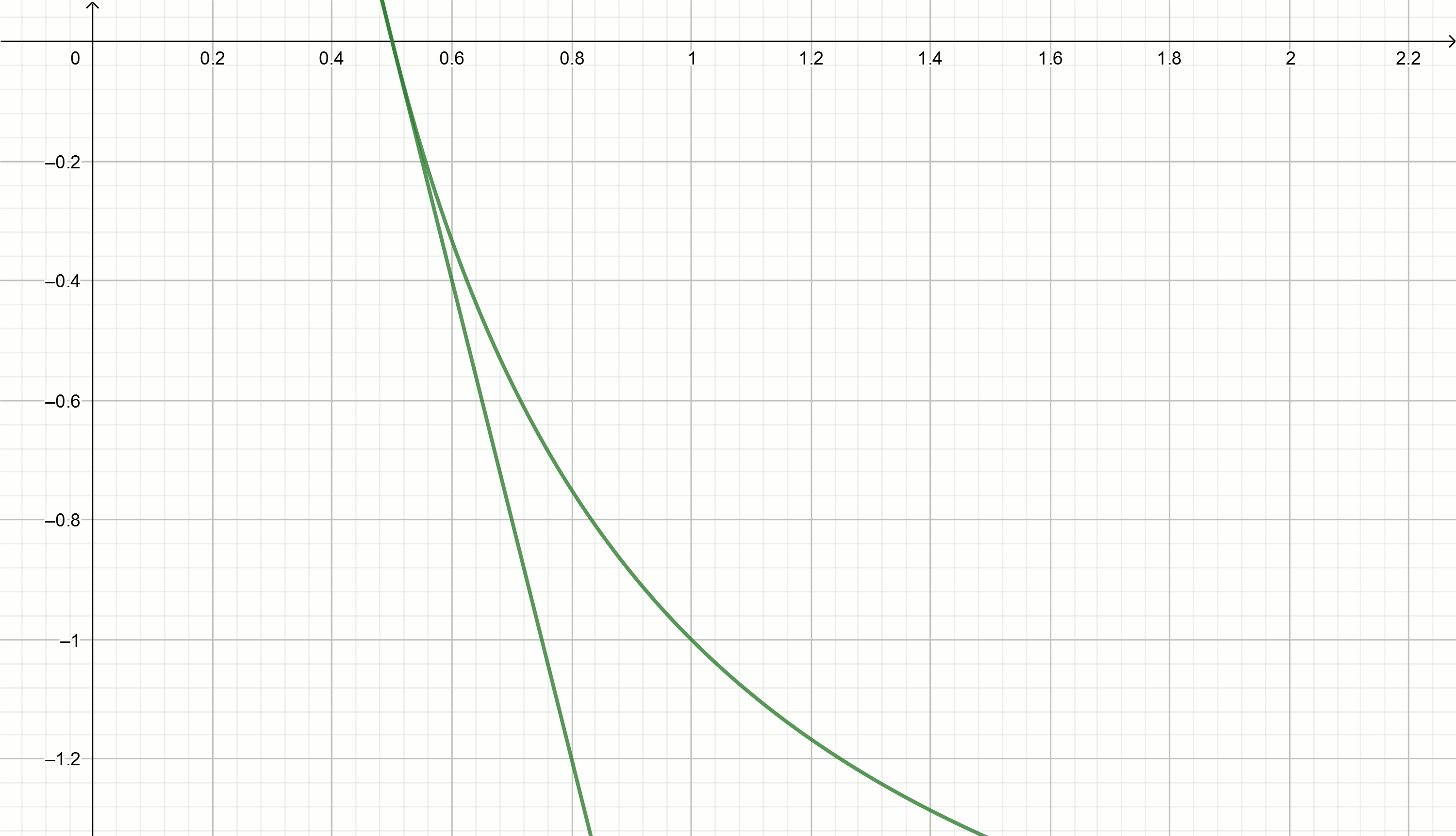
Interpretasi geometris

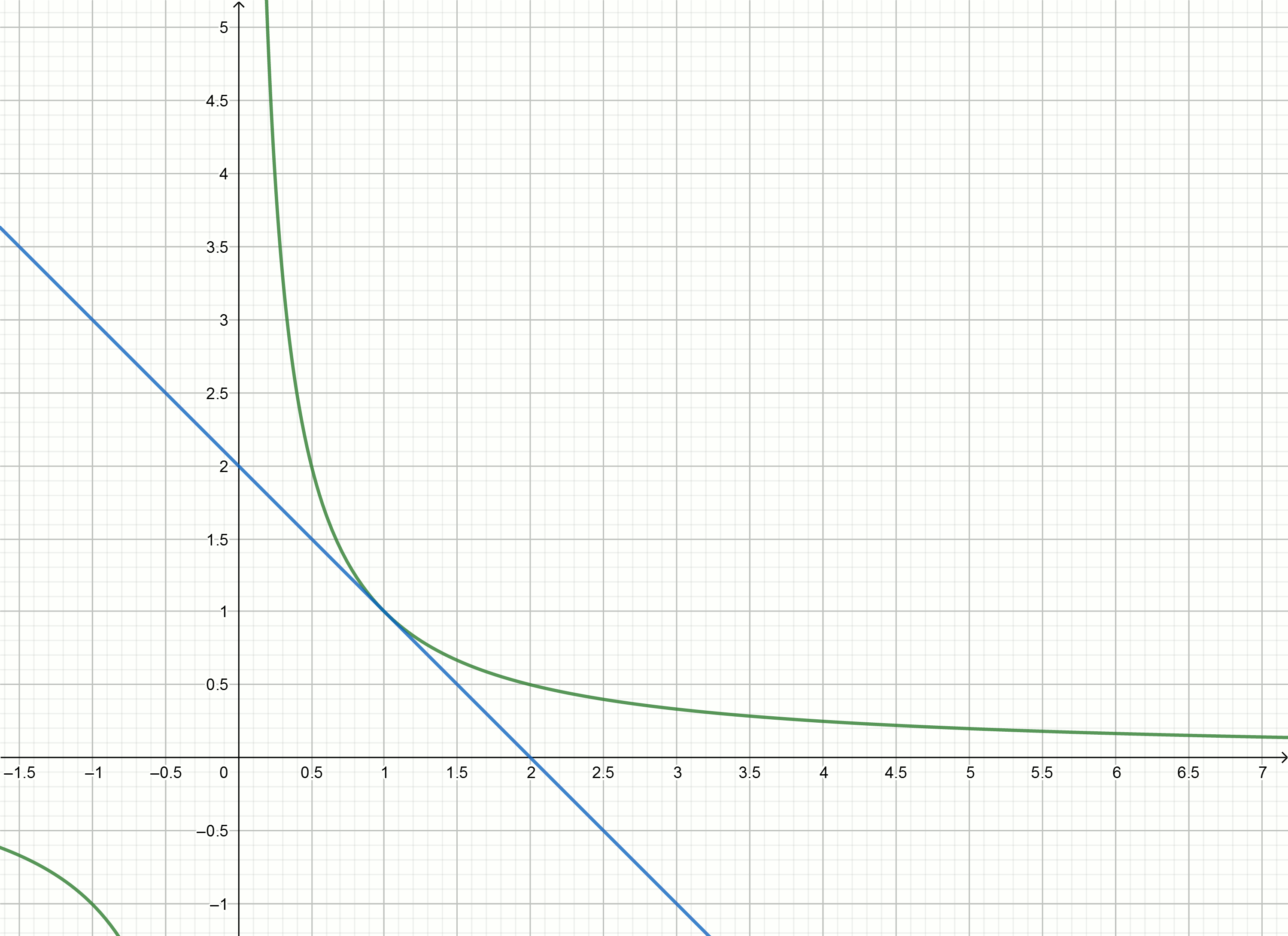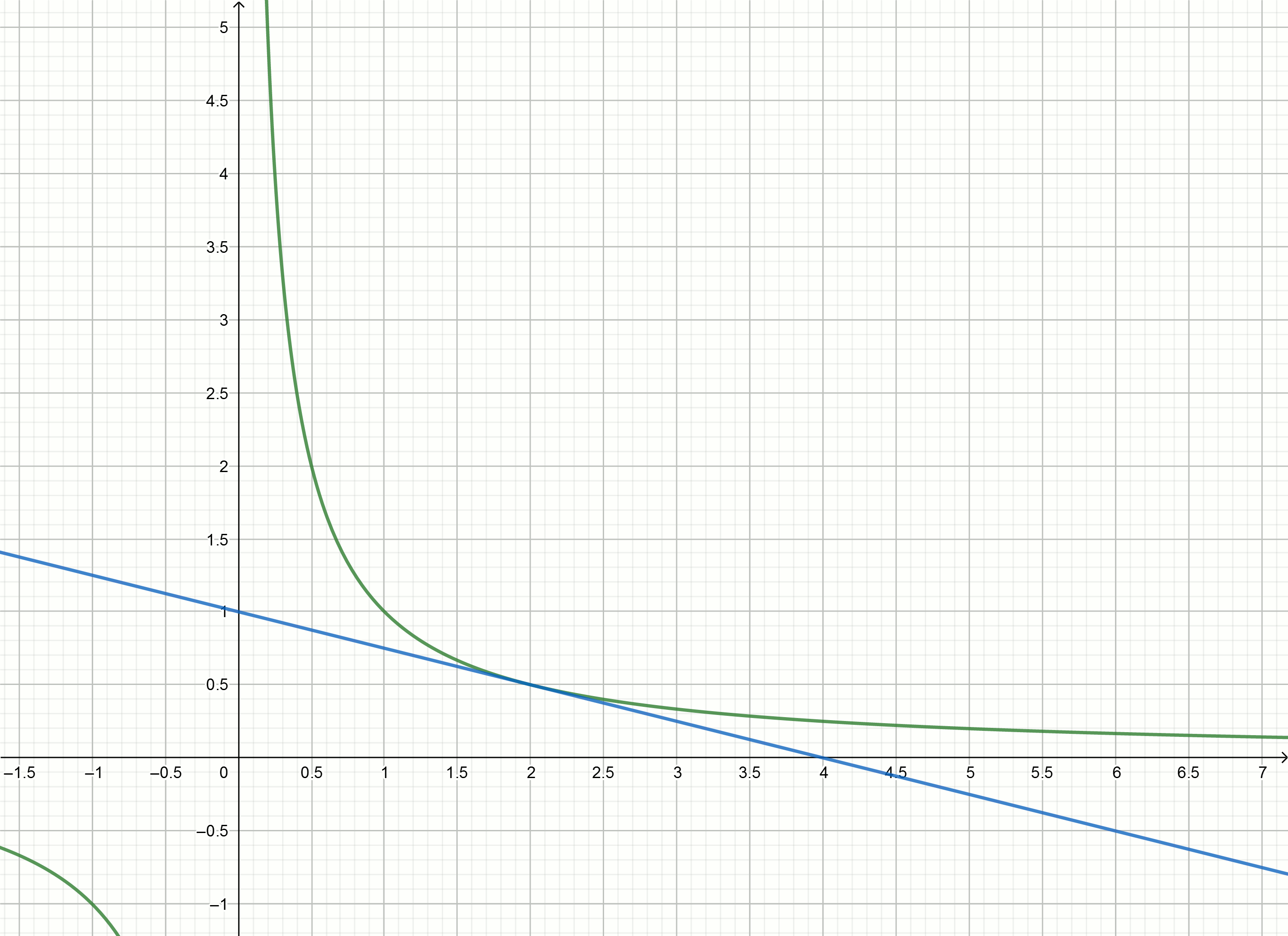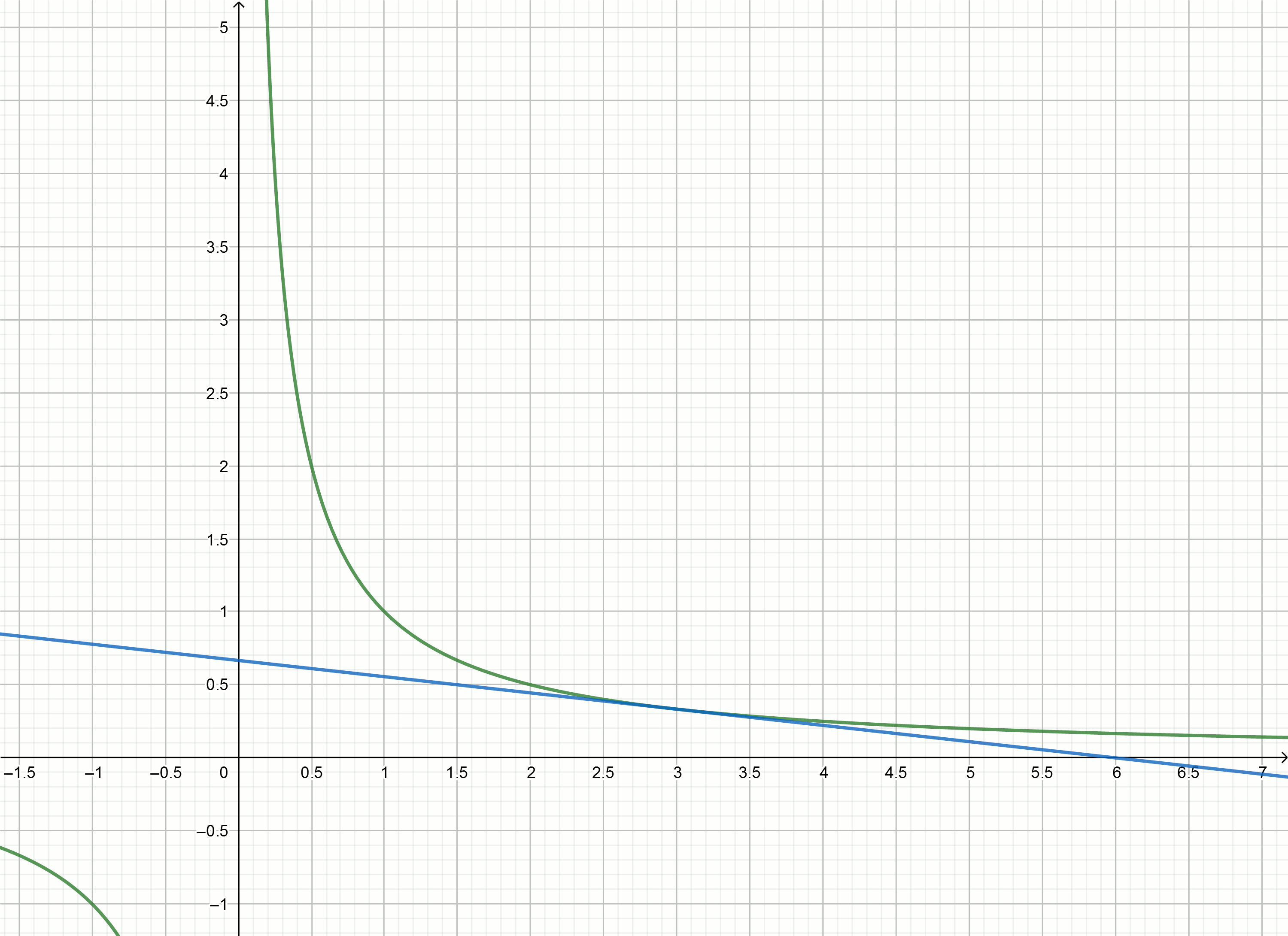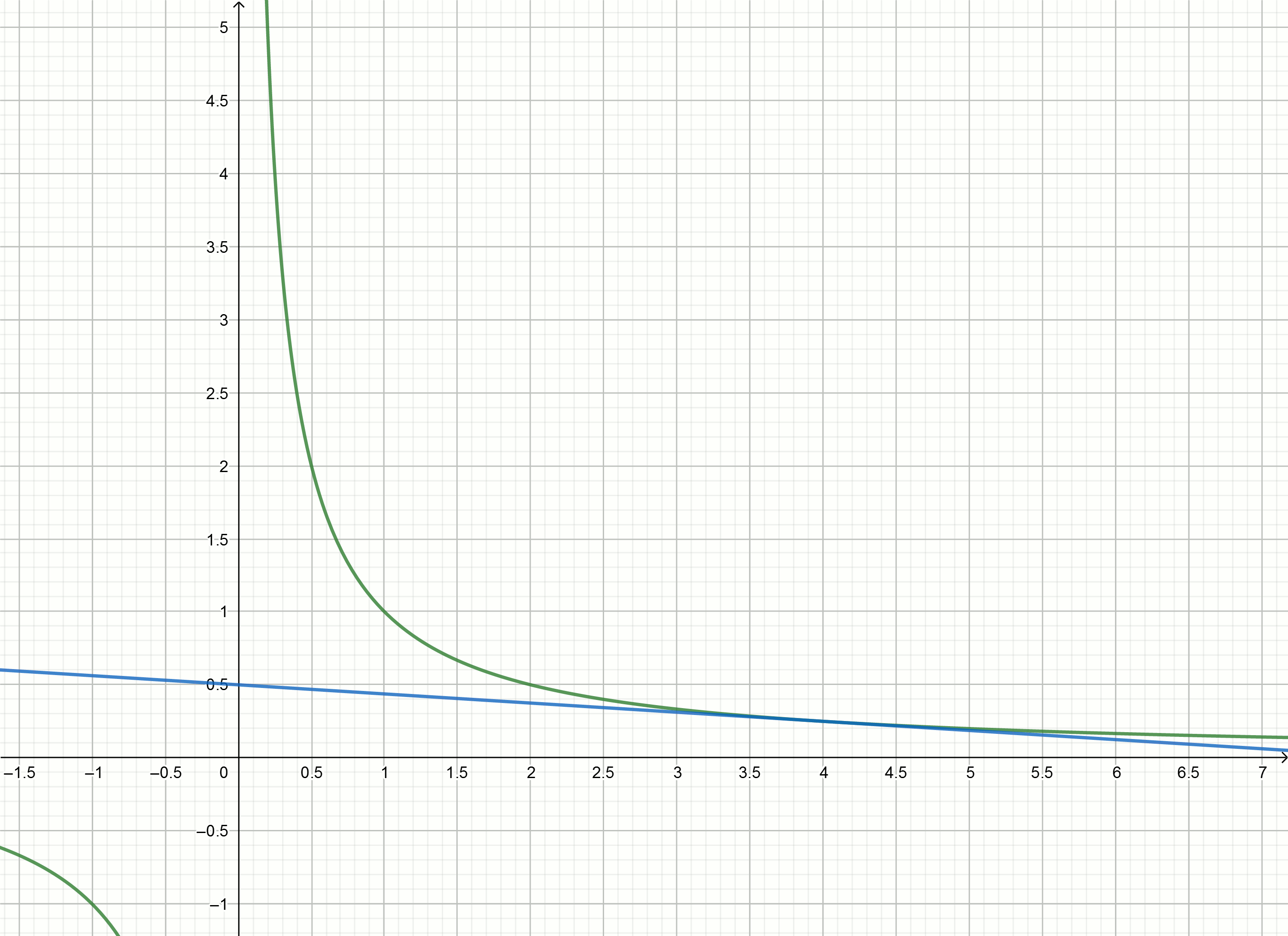
Mari kita coba menggunakan metode tangen untuk memperkirakan angka terbalik.
Garis singgung $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ berfungsi grafik $$$y = \ frac {1} {x}$ diungkapkan oleh rumus $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

Mengganti Angka $$$1,2,3,4, ...$ bukannya $$$x_ {0}$ kita memperoleh persamaan garis singgung

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

Buat grafik ini


Jika Anda memindahkan hiperbola ke bawah $$$\ alpha$ , lalu melintasi sumbu absis pada titik tersebut $$$\ frac {1} {\ alpha}$ .
Persamaan tangen dikonversi menjadi $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ alpha$
Selanjutnya, menyamakan persamaan garis singgung ke nol dan mengekspresikan $$$x$ kita mendapatkan persamaannya $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0})}$

Sebaliknya $$$f (x_ {0})$ pengganti $$$\ frac {1} {x_ {0}} - \ alpha$
Sebaliknya $$$f '(x_ {0})$ pengganti $$$- \ frac {1} {x_ {0} ^ {2}}$

Kami mendapatkan ekspresi $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ alpha) x_ {0} ^ {2}$
Memperluas kurung, kita dapatkan $$$x = x_ {0} + x_ {0} - \ alpha x_ {0} ^ {2}$

Pengganti $$$0,1$ ke dalam persamaan $$$x = x_ {0} (2- \ alpha x_ {0})$ dan lihat nilai apa yang akan “dijalankan” $$$x$ di $$$\ alpha = 2$ kita dapatkan $$$0,1, 0,18, 0,29, 0,42, 0,49, 0,5$

Mengganti nilai-nilai ini dalam persamaan $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ kami langsung

$$

$$y = 0.111 - \ frac {x} {0.897}$$

$$

$$y = 0.222 - \ frac {x} {0.81}$$

$$

$$y = 0,816 - \ frac {x} {0,504}$$

$$

$$y = 0.857 - \ frac {x} {0.49}$$

$$

$$y = 1.5 - \ frac {x} {0.326}$$

$$

$$y = 2 - \ frac {x} {0,25}$$

Ekstraksi akar kuadrat

Kembali ke ekspresi irasional, kami mempertimbangkan metode berulang mengekstraksi akar kuadrat.
Kami akan menulis algoritma menggunakan metode berulang Heron

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

Perhitungan akar kuadrat menggunakan fraksi lanjutan yang digunakan oleh Rafael Bombelli

Untuk menemukan nilainya $$$\ sqrt {n}$ , pertama-tama kita mendefinisikan seluruh perkiraannya: $$$\ sqrt {n} = a \ pm r$ dimana $$$0 <r <1$ . Lalu $$$n = (a \ pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ . Dari sini mudah untuk menyimpulkan itu $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ . Mengganti ekspresi yang dihasilkan dalam rumus $$$\ sqrt {n} = a \ pm r$ , kami mendapatkan ekspansi fraksi lanjutan:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

Jadi, kita dapat menulis algoritma ekstraksi akar kuadrat menggunakan dekomposisi menjadi fraksi lanjutan

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

Secara umum, bilangan real dan kompleks, serta fungsi dari satu atau lebih variabel, dapat berupa pembilang dan penyebut pribadi.
Metode mengekstraksi bagian bilangan bulat memungkinkan seseorang untuk mewakili bilangan irasional dalam bentuk fraksi lanjutan tak hingga dengan unit dalam pembilang (pembilang sering sama dengan kesatuan).
Berikut adalah contoh ekspansi fraksional lanjutan dari angka $$$\ sqrt {5}$ dari buku "Aljabar"

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

Dengan cara ini $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

Pilih bagian integer dari nomor tersebut $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ . Berarti $$$\ sqrt {5} +2$ dapat direpresentasikan sebagai $$$4 + \ alpha$ . Jelas itu $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ oleh karena itu $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ . Sekali lagi, kami menghancurkan irasionalitas dalam pembilang dari istilah kedua:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

Hasilnya adalah:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

Mari kita lakukan langkah serupa lainnya:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

Sangat mudah untuk melihat bahwa proses mengisolasi seluruh bagian dan pembentukan fraksi lanjutan dalam contoh ini tidak berakhir. Di setiap penyebut baru akan muncul $$$4$ dan istilah $$$\ sqrt {5} -2$ . Karena itu, jelas itu $$$\ sqrt {5}$ direpresentasikan sebagai fraksi lanjutan tanpa batas:

$$

$$\ sqrt {5} = [2, 4, 4, 4, ...]$$

Hipotesis

Jika $$$d \ in \ mathbb {N}, \ sqrt {d} \ notin \ mathbb {N}$ kemudian fraksi lanjutan dari angka tersebut $$$\ sqrt {d} + [\ sqrt {d}]$ murni periodik.
Evarist Galois membuktikan hipotesis ini.

Yaitu jika ke bagian non-periodik fraksi $$$[1; 2,2,2, ...] = \ sqrt {2}$ tambahkan seluruh bagian $$$[\ sqrt {2}] = 1$ maka kita mendapatkan pecahan murni periodik $$$[2,2,2, ...]$ .

$$$\ sqrt {3} = [1; 1,2, ...];$
$$$\ sqrt {3} +1 = [2,1, ...]$

$$$\ sqrt {5} = [2; 4,4,4, ...];$
$$$\ sqrt {5} +2 = [4,4,4, ...]$

$$$\ sqrt {6} = [2; 2,4, ...];$
$$$\ sqrt {6} +2 = [4,2, ...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6, ...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1, ...]$


Jika di root dekomposisi sesuai dengan metode Bombelli

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}}$$

tambahkan ke istilah pertama $$$a$ , kami mendapatkan fraksi murni periodik

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}}$$

Tetap membawa fraksi ke bentuk yang lebih akrab (dengan unit dalam pembilang).
Bagilah pembilang dan penyebut pecahan dengan $$$| n-a ^ {2} |$ kami mendapatkan ekspresi

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}}$$

Dengan cara ini

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} + +. ..}}} = [2,2,2, ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} + +. ..}}} = [2,1, ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} + +. ..}}} = [4,4,4, ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} + +. ..}}} = [4,2, ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} + +. ..}}} = [6, \ frac {3} {2}, ...]$$

Kami akan menulis sebuah program yang menghitung perkiraan fraksi lanjutan $$$[6, \ frac {3} {2}, ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
Pada langkah keempat kita dapatkan $$$6 \ frac {3818} {6305}$ yang sama $$$6,60555114 ...$ sementara $$$\ sqrt {13} +3 \ sekitar 6.60555127$ .




PS Mengatasi masalah (“Masalah untuk anak-anak berusia 5 hingga 15 tahun”)
27 . Buktikan bahwa sisa pembagian angka $$$2 ^ {p-1}$ perdana yang aneh
$$$p$ sama dengan $$$1$
(contoh: $$$2 ^ {2} = 3a + 1, 2 ^ {4} = 5b + 1, 2 ^ {6} = 7c + 1, 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ .
Masalah ini dipertimbangkan dalam artikel Amazing Adventures of Lanjutan Fraksi dari majalah Quantum.

Buku:
"Tugas untuk anak-anak dari 5 hingga 15 tahun" V. I. Arnold.
"Kursus kalkulus diferensial dan integral" G. M. Fichtenholtz
"Nomor Teori" A. A. Buchstab
"Di balik halaman buku teks matematika" N. Ya. Vilenkin, L. P. Shibasov, Z. F. Shibasova
"Aljabar" N. Ya. Vilenkin, R. S. Guter, S. I. Schwarzburd
Aritmatika Digital Ercegovac Milos D., Lang Tomas
"Struktur dan interpretasi program komputer" Harold Abelson, Gerald Sassman

Lihat juga
Artikel "Pada satu tugas yang tidak lagi ditawarkan saat wawancara."
Blog Spice Recruitment's Blog memposting tugas wawancara ke berbagai perusahaan.
Tugas untuk wawancara di Yandex.
Dalam video ini, A. Savvateev memecahkan masalah dengan wawancara di Tesla.