Metode numerik untuk memecahkan sistem persamaan nonlinier

Pendahuluan

Banyak masalah yang diterapkan mengarah pada kebutuhan untuk menemukan solusi umum untuk sistem persamaan nonlinier. Tidak ada solusi analitis umum dari sistem persamaan nonlinier yang ditemukan. Hanya ada metode numerik.

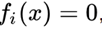
Perlu dicatat fakta menarik bahwa sistem persamaan apa pun atas bilangan real dapat diwakili oleh satu persamaan yang setara, jika kita mengambil semua persamaan dalam bentuk , lipat persegi dan lipat.

Untuk solusi numerik, metode iteratif dari pendekatan yang berurutan (iterasi sederhana) dan metode Newton dalam berbagai modifikasi digunakan. Proses berulang secara umum digeneralisasikan ke kasus sistem persamaan nonlinear dari bentuk:

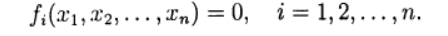
(1)

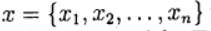
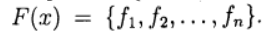
Ditunjukkan oleh vektor tidak diketahui dan mendefinisikan fungsi vektor Kemudian sistem (1) ditulis dalam bentuk persamaan:

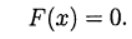
(2)

Sekarang, mari kita kembali ke Python tercinta kita dan catat keunggulannya di antara bahasa pemrograman yang ingin dipelajari [1].



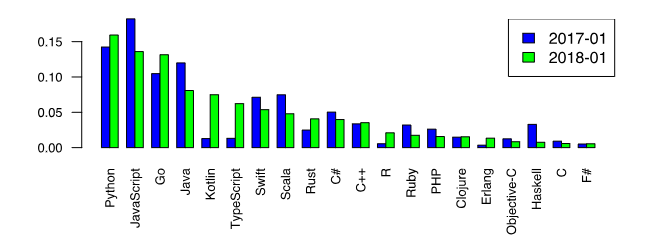
Fakta ini merupakan insentif tambahan untuk mempertimbangkan metode numerik dengan Python. Namun, ada pendapat di kalangan pecinta Python bahwa fungsi perpustakaan khusus, seperti scipy.optimize.root, spsolve_trianular, newton_krylov , adalah pilihan terbaik untuk memecahkan masalah dengan metode numerik.

Sulit untuk tidak setuju dengan ini, jika hanya karena berbagai modul juga mengangkat Python ke puncak popularitas. Namun, ada kasus ketika, bahkan dengan pemeriksaan sepintas, menggunakan metode langsung dikenal tanpa menggunakan fungsi khusus dari SciPy library juga memberikan hasil yang baik. Dengan kata lain, yang baru adalah yang lama terlupakan.

Jadi, dalam publikasi [2], berdasarkan percobaan komputasi yang dilakukan, terbukti bahwa fungsi perpustakaan newton_krylov, yang dirancang untuk memecahkan sistem persamaan nonlinier besar, memiliki setengah kecepatan daripada algoritma TSLS + WD
(dua langkah kuadrat terkecil) diimplementasikan oleh perpustakaan NumPy.

Tujuan dari publikasi ini adalah untuk membandingkan jumlah iterasi, kecepatan, dan yang paling penting, hasil pemecahan masalah model dalam bentuk sistem seratus persamaan aljabar nonlinier menggunakan fungsi perpustakaan scipy.optimize.root dan metode Newton diimplementasikan menggunakan perpustakaan NumPy.

Scipy.optimize.root kemampuan solver untuk memecahkan sistem persamaan aljabar nonlinier secara numerik

Fungsi perpustakaan scipy.optimize.root dipilih sebagai basis perbandingan karena memiliki pustaka metode yang luas yang cocok untuk analisis komparatif.

scipy.optimize.root ( fun, x0, args = (), method = 'hybr', jac = Tidak ada, tol = Tidak ada, callback = Tidak ada, pion = Tidak ada )
fun - Fungsi vektor untuk menemukan root.
x0 –Kondisi awal untuk menemukan root

metode:
hybr - Powell modifikasi dari metode hybrid digunakan;
lm - memecahkan sistem persamaan nonlinier menggunakan metode kuadrat terkecil.
Sebagai berikut dari dokumentasi [3], metode broyden1, broyden2, anderson, linearmixing, diagbroyden, funmixing, krylov adalah metode tepat Newton. Parameter yang tersisa adalah "opsional" dan dapat ditemukan dalam dokumentasi.

Metode untuk memecahkan sistem persamaan nonlinier

Materi yang diberikan di bawah ini memang dapat dibaca dalam literatur, misalnya, dalam [4], tetapi saya menghormati pembaca saya dan, untuk kenyamanannya, menyajikan derivasi metode ini dalam bentuk singkat, jika mungkin. Mereka yang tidak suka formula melewatkan bagian ini.

Dalam metode Newton, pendekatan baru untuk menyelesaikan sistem persamaan (2) ditentukan dari solusi sistem persamaan linear :

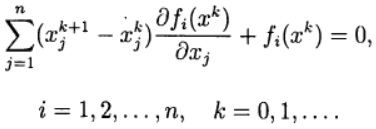
(3)

Definisikan matriks Jacobi:

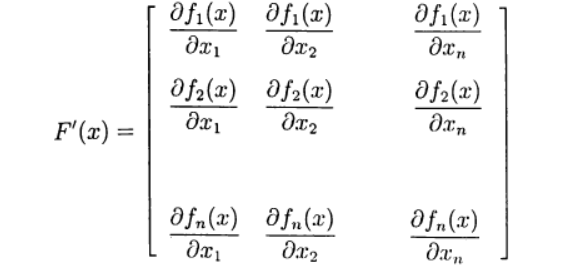
(4)

Kami menulis (3) dalam bentuk:

(5)

Banyak metode satu langkah untuk solusi perkiraan (2) secara analogi dengan metode iteratif dua lapis untuk menyelesaikan sistem persamaan aljabar linier dapat ditulis dalam bentuk:

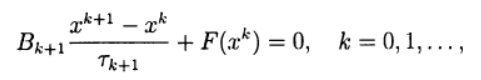
(6)

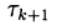
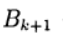
dimana Apakah parameter berulang, a - matriks persegi n x n memiliki kebalikannya.

Saat menggunakan catatan (6), metode Newton (5) sesuai dengan pilihan:



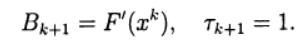
Sistem persamaan linear (5) untuk menemukan pendekatan baru dapat diselesaikan secara iteratif. Dalam hal ini, kami memiliki proses iteratif dua tahap dengan iterasi eksternal dan internal. Misalnya, proses iteratif eksternal dapat dilakukan sesuai dengan metode Newton, dan iterasi internal dapat dilakukan berdasarkan metode iteratif Seidel.

Ketika memecahkan sistem persamaan nonlinear, seseorang dapat menggunakan analog langsung dari metode iteratif standar yang digunakan untuk menyelesaikan sistem persamaan linear. Metode Seidel non-linear sebagaimana diterapkan pada solusi (2) memberikan:

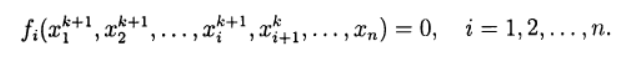
(7)

Dalam hal ini, setiap komponen perkiraan baru dari solusi persamaan nonlinier dapat diperoleh berdasarkan metode iterasi sederhana dan metode Newton dalam berbagai modifikasi. Dengan demikian, kita kembali ke metode iteratif dua tahap di mana iterasi eksternal dilakukan sesuai dengan metode Seidel, dan iterasi internal dilakukan menggunakan metode Newton.

Kesulitan komputasi utama dalam menerapkan metode Newton untuk solusi perkiraan sistem persamaan nonlinier terkait dengan kebutuhan untuk menyelesaikan sistem persamaan linear dengan matriks Jacobi di setiap iterasi , dan matriks ini berubah dari iterasi ke iterasi. Dalam metode Newton yang dimodifikasi, matriks Jacobi hanya dibalik satu kali:

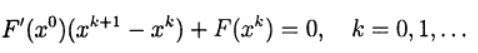
(8)

Pemilihan fungsi model

Pilihan seperti itu bukanlah tugas yang sederhana, karena dengan peningkatan jumlah persamaan dalam sistem sesuai dengan peningkatan jumlah variabel, hasil solusi tidak boleh berubah, karena jika tidak, tidak mungkin untuk melacak kebenaran solusi dari sistem persamaan ketika membandingkan dua metode. Saya membawa solusi berikut untuk fungsi model:

n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Fungsi f menciptakan sistem n persamaan nonlinier, solusinya tidak tergantung pada jumlah persamaan dan sama dengan kesatuan untuk masing-masing variabel n.

Suatu program untuk pengujian pada fungsi model dengan hasil penyelesaian sistem persamaan nonlinier aljabar menggunakan fungsi perpustakaan optim.root untuk berbagai metode menemukan akar

 from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds') 

Hanya salah satu metode yang diberikan dalam dokumentasi [3] yang lulus pengujian pada hasil penyelesaian fungsi model, ini adalah metode 'krylov' .

Solusi untuk n = 100:

Solusi:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Metode iterasi Krylov = 4219
Optimalkan waktu root 7,239 detik:


Kesimpulan: Dengan peningkatan jumlah persamaan hingga setengahnya, tampilan kesalahan dalam solusi terlihat. Dengan peningkatan lebih lanjut dalam n, solusi menjadi tidak dapat diterima, yang dimungkinkan karena adaptasi otomatis ke langkah, alasan yang sama untuk penurunan tajam dalam kinerja. Tapi ini hanya dugaanku.

Program untuk menguji fungsi model dengan hasil penyelesaian sistem persamaan nonlinier aljabar menggunakan program yang ditulis dalam Python 3 dengan mempertimbangkan hubungan akun (1) - (8) untuk menemukan akar menggunakan metode Newton yang dimodifikasi

Solusi untuk n = 100:

Solusi:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Iterasi Newton = 13
Metode Newton waktu 0,496 detik

Solusi untuk n = 200:

Solusi:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1.]
Iterasi Newton = 14
Metode Newton waktu 1,869 detik

Untuk memastikan bahwa program benar-benar menyelesaikan sistem, kami menulis ulang fungsi model untuk menghindari root dengan nilai 1 dalam formulir

 n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Kami mendapatkan:
Solusi:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Iterasi Newton = 16
Metode Newton waktu 0,046 detik

Kesimpulan: Program juga berfungsi ketika fungsi model berubah.

Sekarang kita kembali ke fungsi model awal dan memeriksa rentang yang lebih luas untuk n, misalnya, pada 2 dan 500.
n = 2
Solusi:
[1. 1.]
Iterasi Newton = 6
Metode Newton waktu 0,048 detik
n = 500

Kesimpulan:

Sebuah program yang ditulis dengan Python menggunakan metode Newton yang dimodifikasi, ketika menyelesaikan sistem persamaan nonlinear dari fungsi model yang diberikan, memiliki stabilitas solusi yang lebih tinggi daripada ketika menyelesaikan menggunakan fungsi perpustakaan mengoptimalkan.root (f, x0, metode = 'krylov') untuk metode Krylov. Mengenai kecepatan kesimpulan akhir, tidak mungkin untuk menggambar karena pendekatan yang berbeda untuk pengendalian langkah.

Referensi:

1. Peringkat bahasa pemrograman 2018.
2. Cooper I.V., Faleychik B.V. Proses iteratif non-matriks dengan penekanan rata-rata akar kuadrat untuk sistem persamaan nonlinier besar.
3. scipy.optimize.root.
4. Vabishchevich P.N. Metode numerik: Lokakarya komputasi. - M .: Book House "LIBROCOM", 2010. - 320 p.