Membangun orbit benda langit menggunakan Python

Sistem referensi untuk menentukan orbit

Untuk menemukan lintasan gerakan relatif dalam mekanika klasik, asumsi waktu absolut dalam semua kerangka referensi (baik inersia dan non-inersia) digunakan.

Dengan menggunakan asumsi ini, kami mempertimbangkan gerakan titik yang sama dalam dua kerangka referensi yang berbeda $$$K$ dan $$$K ^ {'}$ dimana yang kedua bergerak relatif terhadap yang pertama dengan kecepatan sewenang-wenang $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ dimana $$$\ vec {R (t)}$ radius vektor yang menggambarkan posisi asal sistem koordinat $$$K ^ {'}$ relatif terhadap kerangka referensi $$$K$ )

Kami akan menggambarkan gerakan suatu titik dalam sistem $$$K ^ {'}$ vektor radius $$$\ vec {r ^ {'}} (t)$ diarahkan dari asal sistem $$$K ^ {'}$ ke posisi titik saat ini. Kemudian gerakan titik yang dipertimbangkan relatif terhadap kerangka referensi $$$K$ dijelaskan oleh vektor radius $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ , (1)

dan kecepatan relatif $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ , (2)

dimana $$$\ dot {\ vec {r ^ {'}}} (t)$ - Kecepatan titik relatif ke sistem $$$K ^ {'}$ ; $$$\ dot {\ vec {R}} (t)$ Kecepatan -frame $$$K ^ {'}$ relatif terhadap kerangka referensi $$$K$ .



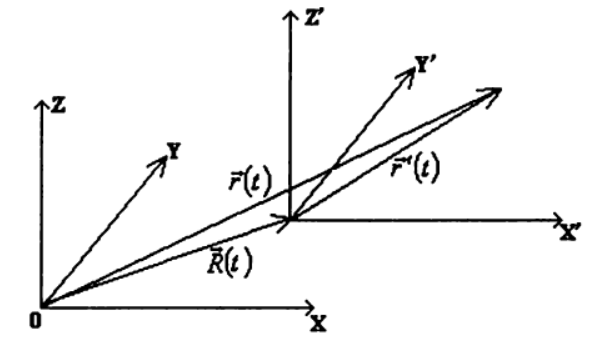
Dengan demikian, untuk menemukan hukum gerak suatu titik dalam kerangka referensi yang sewenang-wenang $$$K$ perlu:

1) mengatur hukum gerak titik - $$$\ vec {r ^ {'}} (t)$ relatif terhadap kerangka referensi $$$K ^ {'}$ ;
2) mengatur hukum gerak - $$$\ vec {R} (t)$ sistem referensi $$$K ^ {'}$ relatif terhadap kerangka referensi $$$K$
3) menentukan hukum gerak titik - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ relatif terhadap kerangka referensi $$$K$ .

Konstruksi orbit bulan dalam kerangka referensi heliosentris

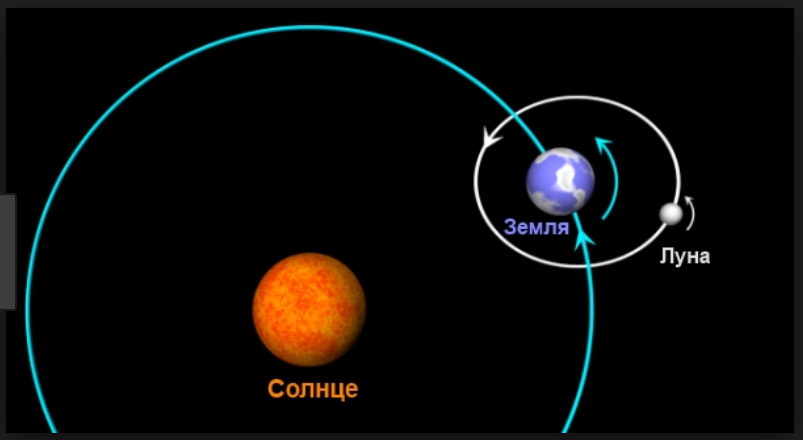
Dalam sistem referensi heliosentris (sistem $$$K$ ) Bumi bergerak dalam lingkaran jari-jari
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km (periode sirkulasi $$$T_ {1} = 3,156 \ cdot 10 ^ {7}$ s.). Bulan, pada gilirannya, bergerak di sekitar Bumi (sistem K ') di sekitar lingkaran jari-jari $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km (periode sirkulasi $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ s Seperti diketahui [1,2], ketika suatu titik material bergerak di sepanjang lingkaran jari-jari $$$R$ dengan kecepatan sudut konstan $$$\ omega$ koordinat vektor jari-jari yang digambar dari titik asal ke posisi titik saat ini berubah menurut hukum:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})}, (3)$$

dimana $$$\ varphi _ {0}$ - fase awal mengkarakterisasi posisi partikel pada saat itu $$$t = 0$ , yang di masa depan kita anggap sama dengan nol. Mengganti dalam (3) $$$R$ pada $$$R_ {1}$ dan $$$R_ {2}$ dan mensubstitusi dalam (1), kita mendapatkan ketergantungan vektor jari-jari bulan dalam sistem koordinat heliosentris tepat waktu:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)}, (4)$$

Ekspresi (4) menetapkan orbit Bulan ( $$$y = y (x (t))$ ) dalam bentuk parametrik, di mana parameternya adalah waktu. Untuk membangun orbit yang diinginkan menggunakan Python, kami menetapkan jari-jari orbit dan periode rotasi Bumi dan Bulan.

Bumi bergerak dalam sistem koordinat heliosentris ( $$$K$ ) radius orbitnya dan periode revolusi masing-masing sama $$$R_ {1} = 1.496 \ cdot 10 ^ {8} km, T_ {1} = 3.156 \ cdot 10 ^ {7} s$ Bulan bergerak mengelilingi bumi dalam sistem koordinat ( $$$K ^ {'}$ ) radius orbitnya dan periode revolusi masing-masing sama $$$R_ {2} = 3,844 \ cdot 10 ^ {5} km, T_ {2} = 2.36 \ cdot 10 ^ {6} s$ .

Mengingat (4), kami menentukan fungsi ketergantungan koordinat pada waktu:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t), y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

Menggunakan (5), kami memperoleh sepasang koordinat untuk orbit bulan:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

Kami menetapkan jumlah titik di mana koordinat N = 1000 dan waktu diskrit pada interval periode rotasi bumi dihitung $$$dt = \ frac {T_ {1}} {N}$ . Kami akan menulis program dan membuat grafik untuk area perubahan koordinat positif:


Kami mendapatkan:


Fig. 1

Jadwal yang dibuat memungkinkan Anda untuk memperluas tugas pelatihan dan melihat seperti apa orbit bulan jika jari-jari orbit bulan adalah $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ . . Jelas bagi pembaca yang bahkan tidak memiliki pengetahuan khusus dalam astronomi bahwa Bulan tidak dapat memiliki orbit seperti itu di bidang non-gravitasi Bumi, dan jari-jari hipotetis digunakan untuk mempelajari kondisi munculnya loop . Kami akan membuat perubahan yang sesuai dengan program:


Kami mendapatkan:


Gbr.2

Membandingkan orbit bulan yang ditunjukkan pada Gambar. 1 dan 2, kami menemukan perbedaan yang signifikan. Untuk menjelaskan alasan perbedaan ini, perlu untuk membandingkan kecepatan linear bulan dalam kasus pertama dan kedua dan kecepatan linear bumi.

Karena arah kecepatan linear Bumi relatif terhadap Matahari, serta arah kecepatan linear Bulan relatif terhadap Bumi, perubahan waktu, dan kecepatan tetap konstan dalam besaran.

Sebagai karakteristik kuantitatif dari rasio kecepatan linear bulan dan bumi dalam sistem koordinat heliosentris, kita harus memilih perbedaan antara modul kecepatan linear bumi dan proyeksi kecepatan linear bulan pada arah vektor kecepatan linear bumi:

$$

$$v_ {o} (t) = \ kiri | \ vec {V} (t) \ kanan | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ kiri | \ vec {V} (t) \ right |}, (7)$$

Kami mendefinisikan fungsi yang menggambarkan hukum perubahan komponen kecepatan Bumi dan Bulan:

$$

$$\ begin {matrix} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {matrix}, (8)$$

Untuk menentukan kecepatan yang dihasilkan, dengan mempertimbangkan proyeksi, kami menggunakan relasi:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

Kami akan menulis sebuah program dengan mempertimbangkan (5), (8), (9) dan jari-jari orbit bulan $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km.


Kami mendapatkan:


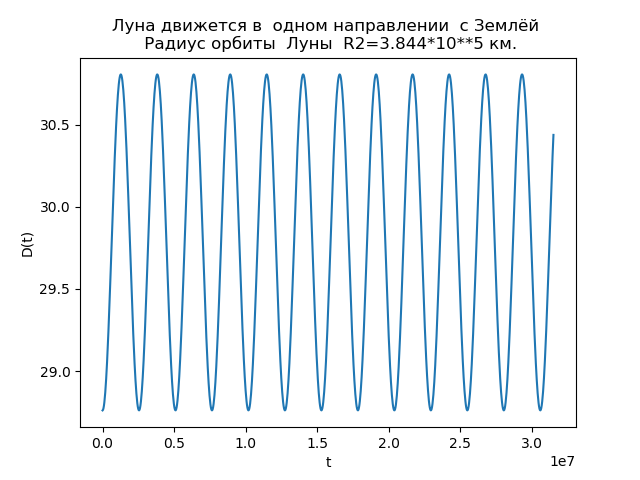Fig. 3.

Kami akan menulis sebuah program dengan mempertimbangkan (5), (8), (9) dan jari-jari orbit Bulan R2 = 3,844 * 10 ** 7 km:


Kami mendapatkan:


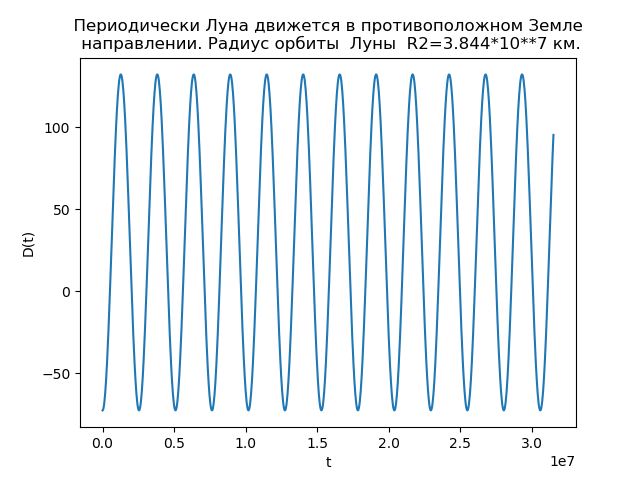Fig. 4.

Analisis ketergantungan memungkinkan kami untuk menjelaskan alasan perbedaan dalam orbit. Fungsi D (t) untuk $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km selalu positif, yaitu, bulan selalu bergerak ke arah gerakan Bumi dan tidak ada loop terbentuk. Di $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ nilai km $$$D (t)$ mengambil nilai negatif, dan ada kalanya bulan bergerak ke arah yang berlawanan dengan arah gerakan bumi, dan oleh karena itu orbitnya memiliki loop. Ini adalah arti dari menggunakan orbit bulan yang tidak ada dalam perhitungan.

Konstruksi orbit Mars dalam kerangka referensi yang terkait dengan Bumi

.


Dalam sistem referensi heliosentris (sistem K), Bumi bergerak dalam lingkaran jari-jari $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km, periode sirkulasi $$$T_ {1} = $ 365.2$ hari, Mars bergerak sepanjang elips, sumbu semi-mayornya $$$am = 2.28 \ cdot 10 ^ {8}$ km, periode revolusi Mars $$$T_ {m} = $ 689,9$ hari., eksentrisitas orbit $$$e = $ 0,09$ [3]. Gerak Bumi dijelaskan oleh jari-jari vektor R (t) yang didefinisikan oleh ekspresi (3). Karena kenyataan bahwa orbit Mars adalah elips, dependensi $$$x = x (t), y = y (t)$ dari waktu diatur secara parametrik [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ , (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ , (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ , (12)

Revolusi elips lengkap berhubungan dengan perubahan dalam parameter <img $$$\ varepsilon$ dari 0 hingga $$$2 \ pi$ . Untuk membangun orbit Mars, perlu untuk menghitung koordinat vektor jari-jari pada saat yang sama yang menggambarkan posisi Bumi dan Mars dalam kerangka referensi heliosentris, kemudian sesuai dengan hubungan $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ menghitung koordinat Mars dalam kerangka referensi yang terkait dengan Bumi.

Untuk membangun orbit Mars dalam kerangka referensi yang terhubung dengan Bumi, kami menggunakan parameter orbit Bumi dan Mars yang telah diberikan sebelumnya, relasi (10) - (12), dan juga relasi untuk koordinat Bumi:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ , (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ , (14)

Perlu dicatat bahwa jumlah periode revolusi Mars di sekitar Matahari adalah $$$K = 9$ , maka jumlah titik di mana perhitungan harus dilakukan dan jarak di antara mereka akan ditentukan dari hubungan:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


Kami mendapatkan:


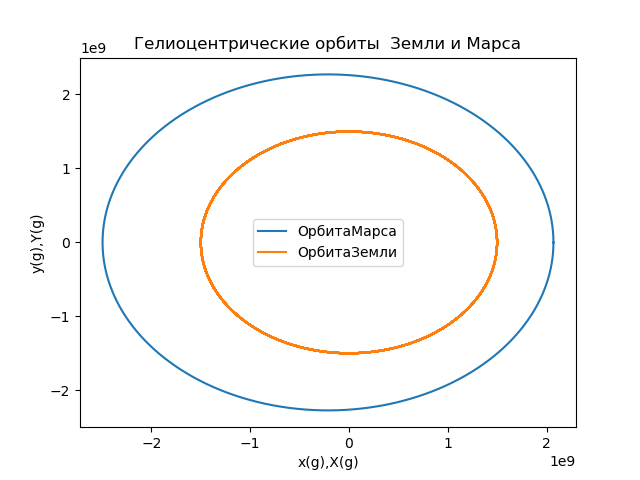Gbr.5

Kami menghitung koordinat vektor radius yang menggambarkan posisi Mars dalam kerangka referensi yang terhubung dengan Bumi, dan membuat orbitnya (Gambar 6) menggunakan relasi:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i} ))$ (16)


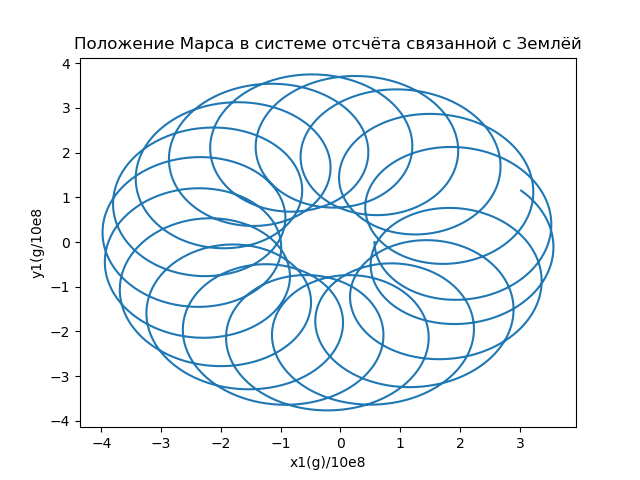Gbr.6

Karakteristik penting lain dari pergerakan Mars (terutama untuk penerbangan antariksa antarplanet) adalah jarak antara Bumi dan Mars (t), yang ditentukan oleh modulus vektor radius yang menggambarkan posisi Mars dalam kerangka referensi yang terkait dengan Bumi. Ketergantungan jarak antara Bumi dan Mars pada waktu yang diukur dalam tahun terestrial disajikan pada Gambar. 7.


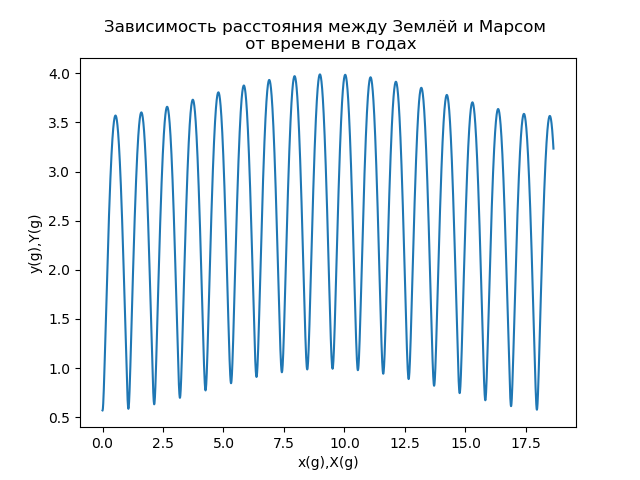Gbr. 7

Analisis ketergantungan yang ditunjukkan pada Gambar. 7 menunjukkan bahwa jarak antara Bumi dan Mars adalah fungsi periodik yang kompleks dari waktu. Jika kita menggunakan terminologi teori sinyal [5], kita dapat mengatakan tentang ketergantungan s (t) bahwa itu adalah sinyal modulasi amplitudo, yang biasanya direpresentasikan sebagai produk dari dua fungsi frekuensi tinggi (pembawa) dan fungsi frekuensi rendah yang mendefinisikan modulasi amplitudo (amplop) :

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

dimana $$$\ bar {u}$ - komponen konstan dari fungsi $$$u (t)$ ; $$$a$ - amplitudo sinyal; $$$\ omega_ {1}$ - frekuensi pembawa; $$$\ Delta a$ - amplitudo fungsi yang mengatur kedalaman modulasi amplitudo; $$$\ omega_ {2}$ - frekuensi fungsi modulasi.

Dari Gambar. 7 dapat dilihat bahwa periode pembawa sekitar 2 tahun, periode fungsi modulasi adalah sekitar 17 tahun] 6].

Konstruksi orbit heliosentris komet Halley

Terakhir kali komet Halley melewati perihelionnya (titik orbit terdekat ke Matahari) pada 9 Februari 1986. (Matahari sendiri dianggap berada di tempat asalnya.)

Koordinat dan komponen kecepatan komet Halley pada saat itu sama $$$p_ {0} = (0,325514, 0,459460, 0,166229)$ dan $$$v_ {0} = (–9.096111, –6.916686, –1.305721)$ masing-masing, dan jarak di sini dinyatakan dalam satuan astronomi panjang - a.u.d., atau hanya a.u. (satuan astronomi, mis., panjang semiotika utama utama dari orbit Bumi), dan waktu dalam tahun. Dalam unit pengukuran ini, persamaan tiga dimensi gerakan komet memiliki bentuk:

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ kanan., (18)$$

(18)

dimana: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


Kami mendapatkan:









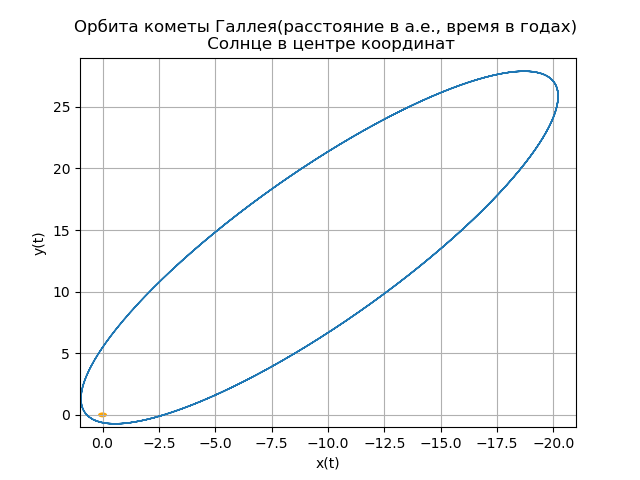
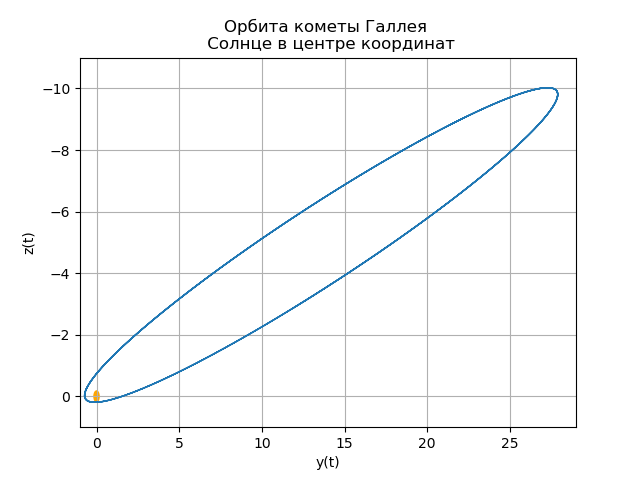
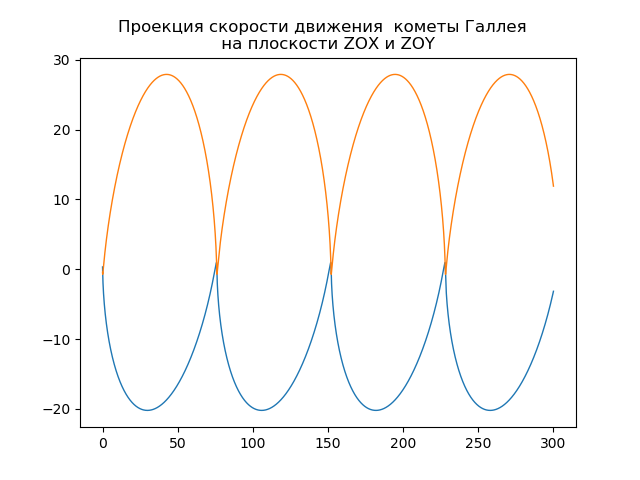Komet Anda sendiri

Coba percobaan. Pada malam hari, Anda memasang teleskop di atas bukit tidak jauh dari rumah Anda. Malam itu harus cerah, tidak berawan, berbintang, dan, jika keberuntungan tersenyum kepadamu: pada pukul 0.30 pagi kamu akan melihat komet baru.

Setelah pengamatan berulang pada malam-malam berikutnya, Anda akan dapat menghitung koordinatnya pada malam pertama itu. Koordinat dalam sistem koordinat heliosentris: P0 = (x0, y0, z0) dan vektor kecepatan v0 = (vx0, vy0, vz0).

Dengan menggunakan data ini, tentukan:

• jarak komet dari Matahari pada perihelion (titik orbit terdekat dengan Matahari) dan pada aphelion (titik orbit terjauh dari Matahari);
• kecepatan komet saat melewati perihelion dan melalui aphelion;
• periode revolusi komet di sekitar Matahari;
• dua tanggal berikutnya komet melewati perihelion.

Jika kita mengukur jarak dalam satuan astronomi, dan waktu dalam tahun, maka persamaan gerak komet akan berbentuk (18). Untuk komet Anda sendiri, pilih mulai koordinat dan kecepatan dari urutan yang sama dengan komet Halley.

Jika perlu, buat kembali pilihan sewenang-wenang dari posisi awal dan vektor kecepatan hingga Anda mendapatkan orbit eksentrik yang masuk akal yang melampaui orbit Bumi (seperti kebanyakan komet sungguhan).

Referensi:

1. Feynman R., Leighton R., Sands M. Feynman Ceramah Fisika. Edisi ke-3. T. 1.-2. M .: Mir, 1977.
2. Matveev A.N. Mekanika dan Teori Relativitas. M.: Lebih tinggi. sekolah., 1986.
3. Ensiklopedia Fisik. T. 3. M .: Big Russian Encyclopedia, 1992.
4. Landau L.D., Lifshits E. M. Kursus di Fisika Teoritis. Mekaniknya. M .: Fu-matgiz, 1958.
5. Baskakov S.I. Rangkaian dan sinyal teknik radio. M.: Lebih tinggi. sekolah., 1988.
6. Porshnev C.V. Simulasi komputer dari proses fisik menggunakan paket mathcad .