Bekerja dengan matriks numerik secara umum dan menyelesaikan sistem persamaan aljabar linear khususnya adalah masalah matematika dan algoritmik klasik yang banyak digunakan dalam pemodelan dan penghitungan kelas besar proses bisnis (misalnya, ketika menghitung biaya). Saat membuat dan mengoperasikan 1C: Konfigurasi perusahaan, banyak pengembang dihadapkan dengan kebutuhan untuk mengimplementasikan algoritma penghitungan SLAU secara manual, dan kemudian dengan masalah menunggu lama untuk suatu solusi.
"1C: Enterprise" 8.3.14 akan berisi fungsionalitas yang dapat secara signifikan mengurangi waktu yang diperlukan untuk menyelesaikan sistem persamaan linear dengan menggunakan algoritma yang didasarkan pada teori grafik.
Ini dioptimalkan untuk digunakan pada data yang memiliki struktur jarang (yaitu, yang mengandung tidak lebih dari 10% koefisien nol dalam persamaan) dan, rata-rata dan dalam kasus terbaik, menunjukkan asimtotik (n⋅log (n) ⋅log (n)), di mana n adalah jumlah variabel, dan dalam kasus terburuk (ketika sistem penuh ~ 100%), perilaku asimptotiknya sebanding dengan algoritma klasik (Θ (n
3 )). Selain itu, pada sistem dengan ~ 10
5 tidak diketahui, algoritma menunjukkan percepatan ratusan kali dibandingkan dengan yang diterapkan di perpustakaan aljabar linier khusus (misalnya,
superlu atau
lapack ).
Penting: artikel dan algoritma yang dideskripsikan membutuhkan pemahaman tentang teori aljabar dan grafik linier pada tingkat tahun pertama sebuah universitas.Penyajian SLAE sebagai grafik
Pertimbangkan sistem persamaan linear linear sederhana:
Perhatian: sistem dihasilkan secara acak dan akan digunakan nanti untuk mendemonstrasikan langkah-langkah algoritmaPada pandangan pertama, sebuah asosiasi dengan objek matematika lain muncul - grafik adjacency grafik. Jadi mengapa tidak mengkonversi data ke daftar adjacency, menghemat RAM saat runtime dan mempercepat akses ke koefisien yang tidak nol?
Untuk melakukan ini, ia cukup untuk mengubah posisi matriks dan menetapkan invarian
"A [i] [j] = z variable variabel ke-i memasuki persamaan j-th dengan koefisien z" , dan kemudian untuk setiap A [i] [j] non-nol yang membangun tepi yang sesuai dari vertex i ke vertex j.
Grafik yang dihasilkan akan terlihat seperti ini:
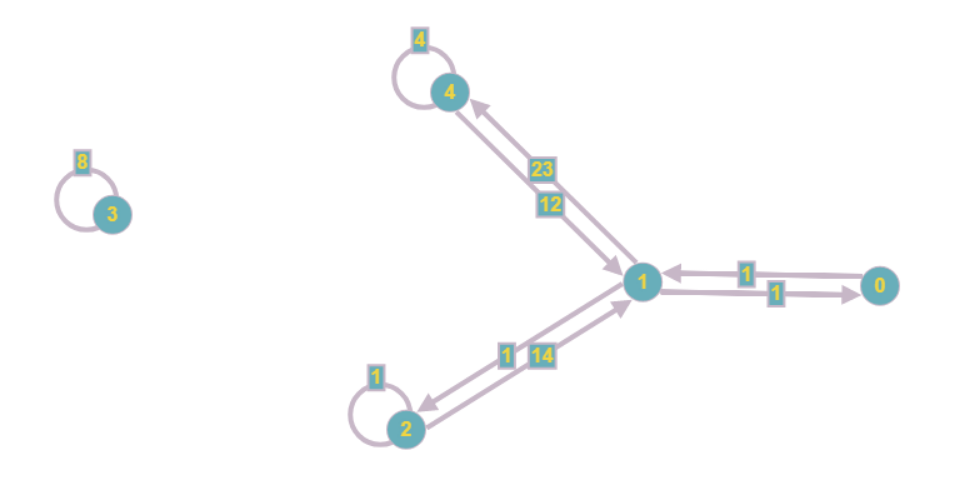
Bahkan secara visual, ternyata menjadi kurang rumit, dan biaya memori asimptotik menurun dari O (n
2 ) menjadi O (n + m), di mana m adalah jumlah koefisien dalam sistem.
Isolasi komponen yang terhubung lemah
Gagasan algoritmik kedua yang muncul dalam pikiran ketika mempertimbangkan entitas yang dihasilkan: penggunaan prinsip "divide and conquer". Dalam hal grafik, ini mengarah ke pemisahan set simpul menjadi komponen yang terhubung lemah.
Biarkan saya mengingatkan Anda bahwa komponen yang terhubung lemah adalah subset dari simpul yang maksimum dalam inklusi bahwa antara dua ada jalur dari tepi dalam grafik tidak terarah. Kita dapat memperoleh grafik yang tidak terarah dari yang asli, misalnya, dengan menambahkan kebalikan dari setiap sisi (dengan penghapusan berikutnya). Kemudian satu simpul koneksi akan mencakup semua simpul yang bisa kita raih ketika kita melihat-lihat grafik secara mendalam.
Setelah pemisahan komponen yang terhubung lemah, grafik akan mengambil bentuk berikut:
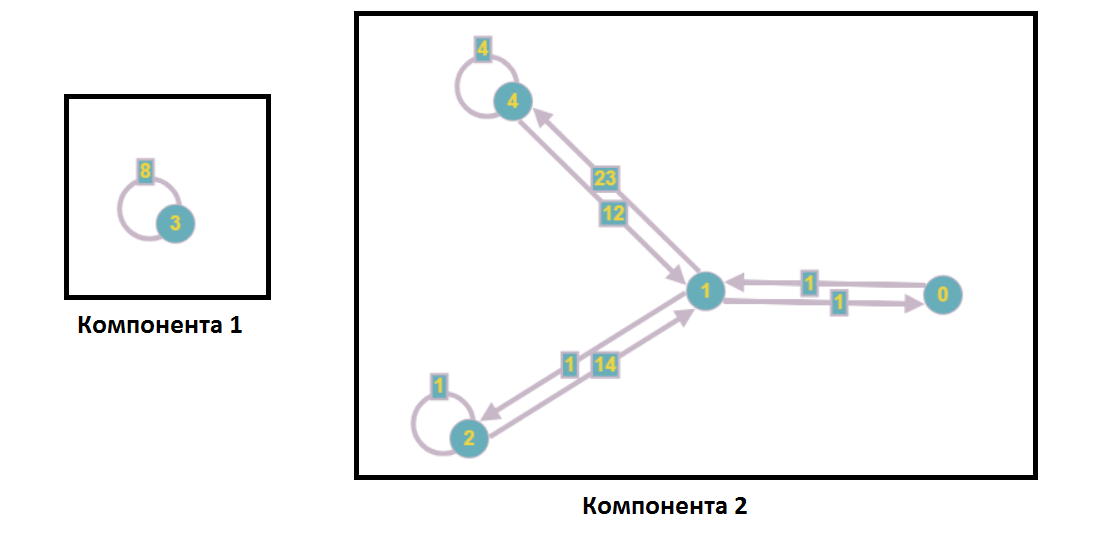
Sebagai bagian dari analisis sistem persamaan linear, ini berarti bahwa tidak ada simpul dari komponen pertama yang dimasukkan dalam persamaan dengan jumlah komponen kedua dan sebaliknya, yaitu, kita dapat menyelesaikan subsistem ini secara mandiri (misalnya, secara paralel).
Pengurangan grafik titik
Langkah selanjutnya dari algoritma ini adalah apa sebenarnya optimasi untuk bekerja dengan matriks jarang. Bahkan dalam grafik dari contoh ada "menggantung" puncak, yang berarti bahwa beberapa persamaan hanya mencakup satu yang tidak diketahui dan, seperti yang kita tahu, nilai yang tidak diketahui ini mudah ditemukan.
Untuk menentukan persamaan seperti itu, diusulkan untuk menyimpan array daftar yang berisi jumlah variabel yang termasuk dalam persamaan yang memiliki jumlah elemen array ini. Kemudian, ketika daftar mencapai ukuran unit, kita dapat mengurangi titik "hanya" yang sangat, dan menginformasikan sisa persamaan dalam persamaan lain di mana titik ini masuk.
Dengan demikian, kita dapat mengurangi vertex 3 dari contoh segera setelah sepenuhnya memproses komponen:
8⋅3=4⇒3=1/2
Kami melanjutkan sama dengan persamaan 0, karena hanya berisi satu variabel:
1⋅x1=1⇒x1=1
Persamaan lain juga akan berubah setelah menemukan hasil ini:
$$ menampilkan $$ 1⋅_1 + 1⋅_2 = 3⇒1⋅_2 = 3-1 = 2 $$ menampilkan $$
Grafik mengambil bentuk berikut:
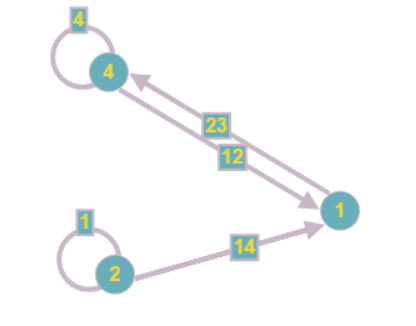
Perhatikan bahwa saat mengurangi satu simpul, yang lain mungkin juga muncul yang juga mengandung satu yang tidak diketahui. Jadi langkah algoritma ini harus diulang sampai setidaknya satu dari simpul dapat dikurangi.
Grafik dibangun kembali
Pembaca yang paling penuh perhatian dapat memperhatikan bahwa suatu situasi dimungkinkan di mana setiap simpul dari grafik akan memiliki tingkat kemunculan setidaknya dua dan tidak mungkin untuk terus secara konsisten mengurangi simpul.
Contoh paling sederhana dari grafik semacam itu: setiap titik memiliki tingkat kemunculan yang sama dengan dua, tidak ada simpul yang dapat dikurangi.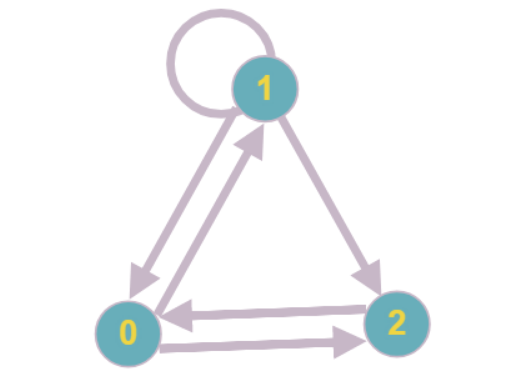
Sebagai bagian dari optimasi untuk matriks jarang, diasumsikan bahwa subgraph tersebut akan berukuran kecil, namun, Anda masih harus bekerja dengan mereka. Untuk menghitung nilai-nilai yang tidak diketahui yang merupakan bagian dari subsistem persamaan, diusulkan untuk menggunakan metode klasik untuk menyelesaikan SLAEs (itulah sebabnya pengantar menunjukkan bahwa untuk matriks di mana semua atau hampir semua koefisien dalam persamaan adalah nol, algoritma kami akan memiliki kompleksitas asimtotik yang sama dengan yang standar. )
Misalnya, Anda dapat membawa set simpul yang tersisa setelah reduksi kembali ke bentuk matriks dan menerapkan
metode Gauss untuk menyelesaikan SLAEs . Dengan demikian, kita akan mendapatkan solusi yang tepat, dan kecepatan algoritme akan berkurang karena pemrosesan bukan keseluruhan sistem, tetapi hanya sebagian saja.
Pengujian Algoritma
Untuk menguji implementasi perangkat lunak dari algoritma, kami mengambil beberapa sistem persamaan nyata volume besar, serta sejumlah besar sistem yang dihasilkan secara acak.
Generasi sistem persamaan acak melalui penambahan berurutan tepi bobot acak antara dua simpul acak. Secara total, sistem itu 5-10% penuh. Ketepatan solusi diverifikasi dengan mengganti jawaban yang diperoleh ke dalam sistem persamaan asli.
Sistem berkisar dari 1.000 hingga 200.000 yang tidak diketahuiUntuk membandingkan kinerja, kami menggunakan perpustakaan paling populer untuk memecahkan masalah aljabar linier, seperti superlu dan lapack. Tentu saja, pustaka-pustaka ini berfokus pada pemecahan kelas masalah yang luas dan solusi SLAE di dalamnya tidak dioptimalkan dengan cara apa pun, sehingga perbedaan dalam kecepatan ternyata menjadi signifikan.
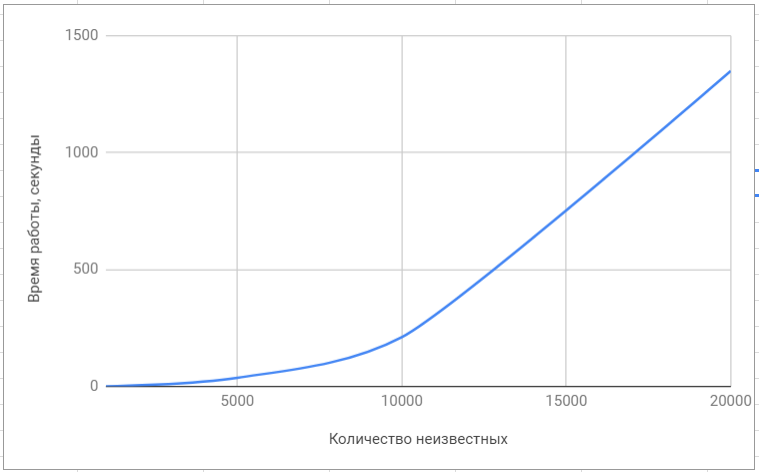Menguji perpustakaan lapack
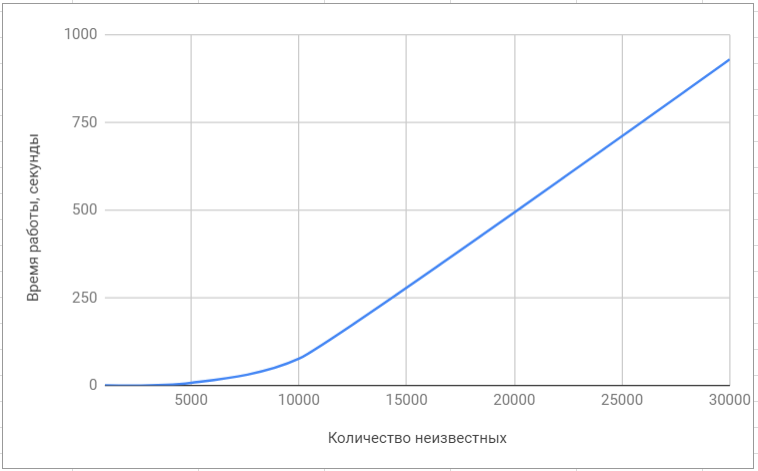Menguji perpustakaan 'superlu'Berikut adalah perbandingan terakhir dari algoritma kami dengan algoritma yang diterapkan di perpustakaan populer:
Kesimpulan
Bahkan jika Anda bukan 1C: Pengembang konfigurasi perusahaan, ide dan metode optimisasi yang dijelaskan dalam artikel ini dapat digunakan oleh Anda tidak hanya ketika menerapkan algoritma untuk menyelesaikan SLAEs, tetapi juga untuk seluruh kelas masalah aljabar linier yang terkait dengan matriks.
Untuk pengembang 1C, kami menambahkan bahwa fungsi baru dari solusi SLAE mendukung penggunaan sumber daya komputasi secara paralel, dan Anda dapat menyesuaikan jumlah utas perhitungan yang digunakan.