Richard Hamming: Bab 20. Pemodelan - III

"Tujuan kursus ini adalah untuk mempersiapkan Anda untuk masa depan teknis Anda."

Masih mempublikasikan 2 bab ...

Pemodelan - III

Saya akan melanjutkan arahan umum yang diberikan pada bab sebelumnya, tetapi kali ini saya akan berkonsentrasi pada ungkapan lama “Sampah masuk - sampah keluar”, yang sering disingkat GIGO (sampah masuk, sampah keluar). Idenya adalah bahwa jika Anda memasukkan data yang dikumpulkan secara tidak akurat dan ekspresi yang salah didefinisikan pada input, maka output yang Anda dapatkan hanya hasil yang salah. Sebaliknya juga secara implisit diasumsikan: dari ketersediaan data input yang akurat, diperoleh hasil yang benar. Saya akan menunjukkan bahwa kedua asumsi ini bisa salah.

Seringkali, pemodelan didasarkan pada penyelesaian persamaan diferensial, jadi untuk permulaan kami akan mempertimbangkan persamaan diferensial paling sederhana dari urutan pertama formulir



Seperti yang Anda ingat, bidang arah adalah garis yang dibangun pada setiap titik bidang xy, dengan koefisien sudut yang diberikan oleh persamaan diferensial (Gambar 20.I). Sebagai contoh, persamaan diferensial memiliki bidang arah yang ditunjukkan pada Gambar 20.II.





Gambar 20.I

Untuk setiap lingkaran konsentris,



sedemikian rupa sehingga kemiringan garis selalu sama dan tergantung pada nilai k. Kurva seperti itu disebut isoclines .

Sekarang mari kita lihat bidang arah persamaan diferensial lain (Gambar 20.III). Di sisi kiri kita melihat bidang arah yang berbeda, yang berarti bahwa perubahan kecil dalam nilai awal atau kesalahan perhitungan kecil akan menyebabkan perbedaan besar dalam nilai-nilai di tengah jalan. Di sisi kanan kita melihat bahwa bidang arah konvergen. Ini berarti bahwa dengan perbedaan yang lebih besar di tengah jalan, perbedaan nilai di ujung kanan akan kecil. Contoh sederhana ini menunjukkan bagaimana kesalahan kecil bisa menjadi besar, kesalahan besar kecil, dan terlebih lagi, bagaimana kesalahan kecil bisa menjadi besar dan kemudian kecil lagi. Oleh karena itu, keakuratan solusi tergantung pada interval spesifik di mana solusi dihitung. Tidak ada akurasi umum absolut.



Gambar 20.II



Gambar 20.III

Pertimbangan ini dibangun untuk fungsi


yang merupakan solusi untuk persamaan diferensial



Anda mungkin membayangkan "pipa" yang pertama kali mengembang dan kemudian menyempit di sekitar "solusi yang tepat dan tepat" dari persamaan tersebut. Representasi seperti itu sangat cocok untuk kasus dua pengukuran, tetapi ketika saya memiliki sistem n persamaan diferensial seperti - 28 dalam kasus masalah rudal pencegat untuk Angkatan Laut yang disebutkan sebelumnya - maka "pipa" di sekitar solusi yang benar untuk persamaan tidak seperti apa yang tampaknya sekilas. Gambar yang terdiri dari empat lingkaran dalam dua dimensi mengarah ke paradoks n-dimensi untuk ruang sepuluh dimensi yang dijelaskan dalam Bab 9. Ini hanyalah pandangan lain tentang masalah pemodelan yang stabil dan tidak stabil, yang dijelaskan dalam bab sebelumnya. Kali ini saya akan memberikan contoh spesifik terkait dengan persamaan diferensial.

Bagaimana kita menyelesaikan persamaan diferensial secara numerik? Dimulai dengan persamaan diferensial orde pertama yang biasa, kami menggambar bidang arah. Tugas kita adalah memiliki nilai awal yang diberikan, menghitung nilai pada tempat terdekat yang menarik bagi kita. Jika kita mengambil koefisien kemiringan lokal dari garis yang diberikan oleh persamaan diferensial dan mengambil langkah kecil ke depan sepanjang garis singgung, maka kita hanya akan memperkenalkan kesalahan kecil (Gambar 20.IV).

Dengan menggunakan titik baru ini, kita akan pindah ke titik berikutnya, tetapi seperti dapat dilihat pada gambar, kita secara bertahap menyimpang dari kurva yang benar, karena kita menggunakan koefisien kemiringan dari langkah sebelumnya, dan bukan koefisien kemiringan sejati untuk interval saat ini. Untuk menghindari efek ini, kami "memprediksi" nilai tertentu, kemudian menggunakannya untuk memperkirakan koefisien sudut pada titik ini (menggunakan persamaan diferensial), dan kemudian menggunakan nilai rata-rata koefisien sudut pada dua batas interval sebagai koefisien sudut untuk interval ini.

Kemudian, dengan menggunakan kemiringan rata-rata ini, kita selangkah lebih maju, kali ini menggunakan rumus "koreksi". Jika nilai yang diperoleh menggunakan rumus "perkiraan" dan "koreksi" cukup dekat, maka kami menganggap bahwa perhitungan kami cukup akurat, jika tidak, kita harus mengurangi ukuran langkah. Jika perbedaan antara nilai terlalu kecil, maka kita harus meningkatkan ukuran langkah. Jadi, skema prediktor-korektor tradisional memiliki mekanisme bawaan untuk memeriksa kesalahan pada setiap langkah, tetapi kesalahan ini pada langkah tertentu sama sekali tidak dan sama sekali tidak merupakan akumulasi kesalahan yang umum! Sangat jelas bahwa akumulasi kesalahan tergantung pada apakah bidang arah menyatu atau menyimpang.



Gambar 20.IV



Gambar 20.V

Kami menggunakan garis lurus sederhana untuk langkah perkiraan dan koreksi. Menggunakan polinomial dengan derajat yang lebih tinggi memberikan hasil yang lebih akurat; polinomial kuartal-derajat biasanya digunakan (solusi persamaan diferensial dengan metode Adams-Bashfort, metode Milne, metode Hamming, dll.). Jadi, kita harus menggunakan nilai fungsi dan turunannya di beberapa titik sebelumnya untuk memprediksi nilai fungsi pada titik berikutnya, setelah itu kita menggunakan substitusi nilai ini dalam persamaan diferensial dan memperkirakan nilai baru dari koefisien sudut. Menggunakan nilai baru dan sebelumnya dari koefisien sudut serta nilai fungsi yang diinginkan, kami mengoreksi nilai yang diperoleh. Sudah waktunya untuk memperhatikan bahwa korektor tidak lebih dari filter rekursif digital di mana nilai input adalah turunan dan nilai output adalah nilai dari fungsi yang diinginkan.

Stabilitas dan konsep-konsep lain yang dibahas sebelumnya tetap relevan. Seperti disebutkan sebelumnya, ada loop umpan balik tambahan untuk solusi prediksi persamaan diferensial, yang pada gilirannya digunakan dalam menghitung koefisien sudut yang disesuaikan. Kedua nilai ini digunakan dalam menyelesaikan persamaan diferensial, filter digital rekursif hanyalah formula, dan tidak lebih. Namun, mereka bukan karakteristik transfer, karena mereka umumnya dipertimbangkan dalam teori filter digital. Dalam hal ini, perhitungan nilai-nilai persamaan diferensial berlangsung. Dalam hal ini, perbedaan antara pendekatan adalah signifikan: dalam filter digital, sinyal diproses secara linear, sedangkan dalam menyelesaikan persamaan diferensial ada nonlinier, yang diperkenalkan dengan menghitung nilai turunan dari fungsi. Ini tidak sama dengan filter digital.

Jika Anda memecahkan sistem persamaan diferensial n, maka Anda berurusan dengan vektor komponen n. Anda memperkirakan nilai selanjutnya dari setiap komponen, mengevaluasi setiap n derivatif, menyesuaikan masing-masing nilai yang diprediksi, dan kemudian menerima hasil perhitungan pada langkah ini atau menolaknya jika kesalahan lokal terlalu besar. Anda cenderung menganggap kesalahan kecil sebagai "pipa" yang mengelilingi jalur terhitung yang sebenarnya. Dan lagi, saya mendorong Anda untuk mengingat paradoks empat lingkaran dalam ruang dimensi tinggi. "Pipa" semacam itu mungkin tidak seperti yang terlihat pada pandangan pertama.

Sekarang izinkan saya menunjukkan perbedaan yang signifikan antara kedua pendekatan: metode komputasi dan teori filter digital. Dalam buku teks umum, hanya metode matematika komputasi yang dideskripsikan sebagai fungsi oleh polinomial. Filter rekursif menggunakan frekuensi dalam formula evaluasi! Ini menyebabkan perbedaan yang signifikan!

Untuk melihat perbedaannya, mari kita bayangkan bahwa kita sedang mengembangkan simulator pendaratan manusia di Mars. Pendekatan klasik berkonsentrasi pada bentuk lintasan pendaratan dan menggunakan pendekatan polinomial untuk daerah setempat. Jalur yang dihasilkan akan memiliki titik istirahat dalam akselerasi, karena kami langkah demi langkah bergerak dari interval ke interval. Dalam hal pendekatan frekuensi, kami akan fokus untuk mendapatkan frekuensi yang tepat dan membiarkan lokasinya menjadi seperti apa. Dalam kasus yang ideal, kedua lintasan akan sama, tetapi dalam praktiknya keduanya dapat berbeda secara signifikan.

Kenaikan mana yang harus saya gunakan? Semakin Anda memikirkannya, semakin Anda akan cenderung untuk percaya bahwa pilot di simulator ingin mendapatkan "rasa" dari perilaku modul pendaratan, dan tampaknya respons frekuensi simulator harus "dirasakan" dengan baik oleh pilot. Jika lokasi sedikit berbeda, loop umpan balik akan mengkompensasi penyimpangan ini selama proses pendaratan, tetapi jika "perasaan" kontrol akan berbeda selama penerbangan nyata, pilot akan khawatir tentang "sensasi" baru yang tidak ada dalam simulator. Bagi saya selalu tampak bahwa simulator harus mempersiapkan pilot untuk sensasi nyata sebanyak mungkin (tentu saja, kita tidak dapat mensimulasikan gravitasi rendah di Mars untuk waktu yang lama), sehingga mereka merasa nyaman ketika pada kenyataannya mereka menghadapi situasi di mana mereka berulang kali ditemui di simulator. Sayangnya, kita tahu terlalu sedikit tentang apa yang "dirasakan" pilot itu. Apakah pilot hanya merasakan frekuensi aktual dari ekspansi Fourier, atau apakah mereka juga merasakan frekuensi Laplace memudar kompleks (atau mungkin kita harus menggunakan wavelet?). Apakah pilot yang berbeda merasakan hal yang sama? Kita perlu tahu lebih banyak daripada yang kita tahu sekarang tentang kondisi desain penting ini.

Situasi yang dijelaskan di atas adalah kontradiksi standar antara pendekatan matematika dan teknik untuk memecahkan masalah. Pendekatan ini memiliki tujuan yang berbeda dalam menyelesaikan persamaan diferensial (seperti dalam banyak masalah lain), oleh karena itu mereka mengarah pada hasil yang berbeda. Jika Anda datang dengan pemodelan, Anda akan melihat bahwa ada nuansa tersembunyi yang ternyata menjadi sangat penting dalam praktik, tetapi tentang mana matematikawan yang tidak tahu apa-apa dan akan dengan cara apa pun menyangkal konsekuensi dari mengabaikannya. Mari kita lihat dua jalur (Gambar 20.IV), yang secara kasar saya perkirakan. Kurva atas lebih akurat menggambarkan lokasi, tetapi lengkungan memberikan "sensasi" yang sama sekali berbeda dibandingkan dengan dunia nyata, kurva kedua lebih keliru di lokasi, tetapi memiliki akurasi yang lebih besar dalam hal "sensasi". Saya sekali lagi menunjukkan dengan jelas mengapa saya percaya bahwa seseorang dengan pemahaman yang mendalam tentang bidang subjek masalah juga harus memahami metode matematika untuk menyelesaikannya, dan tidak bergantung pada metode solusi tradisional.

Sekarang saya ingin menceritakan kisah lain tentang hari-hari awal pengujian sistem pertahanan rudal Nike. Pada saat itu, uji coba lapangan sedang berlangsung di White Sands, yang juga disebut "uji coba telepon lapangan." Ini adalah uji peluncuran di mana roket harus mengikuti lintasan yang telah ditentukan dan meledak pada saat terakhir, sehingga semua energi ledakan tidak melampaui wilayah tertentu dan menyebabkan lebih banyak kerusakan, yang lebih baik daripada setetes bagian individu roket di tanah, yang Seharusnya seharusnya melakukan sedikit kerusakan. Tujuan dari tes ini adalah untuk mendapatkan pengukuran nyata dari gaya angkat dan seret sebagai fungsi ketinggian dan kecepatan penerbangan untuk melakukan debug dan meningkatkan desain.

Ketika saya bertemu dengan teman saya yang telah kembali dari pengujian, dia berkeliaran di koridor Bell Laboratories dan terlihat agak menyedihkan. Mengapa Karena dua dari enam peluncuran pertama yang dijadwalkan gagal di tengah penerbangan dan tidak ada yang tahu mengapa. Data yang diperlukan untuk tahap desain lebih lanjut tidak tersedia, yang berarti masalah serius bagi seluruh proyek. Saya mengatakan bahwa jika dia dapat memberi saya persamaan diferensial yang menggambarkan penerbangan, maka saya dapat menempatkan gadis itu untuk menyelesaikannya (mendapatkan akses ke komputer besar di akhir 1940-an itu tidak mudah). Setelah sekitar satu minggu, mereka memberikan tujuh persamaan diferensial orde pertama dan gadis itu siap memulai. Tapi apa kondisi awal sesaat sebelum dimulainya masalah dalam penerbangan? (Pada masa itu, kami tidak memiliki daya komputasi yang cukup untuk dengan cepat menghitung seluruh jalur penerbangan.) Mereka tidak tahu! Data telemetri tidak dapat dipahami sesaat sebelum kegagalan. Saya tidak terkejut dan itu tidak mengganggu saya. Jadi, kami menggunakan nilai estimasi ketinggian, kecepatan penerbangan, sudut serang, dll. - satu syarat awal untuk masing-masing variabel yang menggambarkan jalur penerbangan. Dengan kata lain, saya memiliki sampah di pintu masuk. Tetapi sebelumnya saya menyadari bahwa sifat dari tes lapangan yang kami disimulasikan sedemikian rupa sehingga penyimpangan kecil dari lintasan yang diusulkan secara otomatis diperbaiki oleh sistem panduan! Saya berurusan dengan bidang arah yang sangat konvergen.

Kami menemukan bahwa roket itu stabil di sepanjang sumbu melintang dan vertikal, tetapi ketika salah satu dari mereka stabil, kelebihan energi menyebabkan osilasi di sepanjang sumbu lainnya. Dengan demikian, tidak hanya osilasi sepanjang sumbu transversal dan vertikal, tetapi juga transmisi periodik energi yang meningkat di antara mereka, yang disebabkan oleh rotasi roket di sekitar sumbu longitudinalnya. Segera setelah kurva yang dihitung untuk sebagian kecil lintasan diperlihatkan, semua orang segera menyadari bahwa stabilisasi silang tidak diperhitungkan, dan semua orang tahu cara memperbaikinya. Jadi, kami mendapat solusi yang juga memungkinkan kami membaca data telemetri rusak yang diperoleh selama pengujian, dan untuk mengklarifikasi periode transfer energi - pada kenyataannya, memberikan persamaan diferensial yang benar untuk perhitungan. Saya punya sedikit pekerjaan, kecuali untuk memastikan bahwa gadis dengan kalkulator desktop dengan jujur ​​menghitung semuanya. Jadi, pada bulan Mei, manfaatnya adalah memahami bahwa (1) kita dapat mensimulasikan apa yang terjadi (sekarang ini merupakan rutinitas dalam menyelidiki kecelakaan, tetapi kemudian merupakan inovasi) dan (2) bidang arah menyatu, sehingga kondisi awal mungkin tidak ditentukan secara tepat.

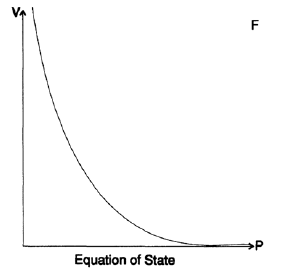
Saya menceritakan kisah ini kepada Anda untuk menunjukkan bahwa prinsip GIGO tidak selalu berhasil. Kisah serupa terjadi pada saya selama simulasi bom awal di Los Alamos. Perlahan-lahan, saya mulai memahami bahwa perhitungan kami, yang dibangun untuk persamaan keadaan, didasarkan pada data yang agak tidak akurat. Persamaan keadaan menghubungkan tekanan dan kepadatan suatu zat (juga suhu, tetapi saya akan menghilangkannya dalam contoh ini). Data dari laboratorium tekanan tinggi, perkiraan yang diperoleh dari studi gempa bumi, kepadatan inti bintang dan teori asimtotik tekanan tak terbatas digambarkan sebagai titik pada kertas grafik yang sangat besar (Gambar 20.VII). Kemudian, menggunakan pola, kami menggambar kurva yang menghubungkan titik-titik yang tersebar. Kemudian, berdasarkan kurva ini, kami membangun tabel nilai fungsi dengan akurasi 3 tempat desimal. Ini berarti bahwa kita hanya mengasumsikan 0 atau 5 di tempat desimal ke-4. Kami menggunakan data ini untuk membuat tabel hingga desimal 5 dan 6. Berdasarkan tabel ini, perhitungan lebih lanjut kami dibangun. Pada waktu itu, seperti yang telah saya sebutkan, saya adalah semacam kalkulator, dan pekerjaan saya adalah menghitung dan dengan demikian membebaskan fisikawan dari pekerjaan ini, untuk memungkinkan mereka melakukan pekerjaan mereka.



Gambar 20.VII

Setelah perang berakhir, saya tinggal di Los Alamos selama setengah tahun lagi, dan salah satu alasan saya melakukan ini adalah karena saya ingin memahami bagaimana data yang tidak akurat dapat menyebabkan simulasi desain akhir yang akurat. Saya memikirkan hal ini untuk waktu yang lama, dan saya menemukan jawabannya. Di tengah perhitungan, kami menggunakan perbedaan tingkat kedua yang terbatas. Perbedaan urutan pertama menunjukkan nilai gaya pada satu sisi setiap shell, dan perbedaan shell yang berdekatan di kedua sisi memberikan gaya yang dihasilkan, yang menggerakkan shell. Kami terpaksa menggunakan cangkang tipis, jadi kami mengurangkan angka yang sangat dekat satu sama lain, dan kami perlu menggunakan banyak digit setelah titik desimal. Studi lebih lanjut menunjukkan bahwa ketika "benda" meledak, kulit bergerak ke atas sepanjang kurva, dan mungkin kadang-kadang sebagian bergeser kembali, sehingga setiap kesalahan lokal dalam persamaan negara dekat dengan nilai rata-rata. Sangat penting untuk mendapatkan kelengkungan persamaan negara dan, sebagaimana telah dicatat, rata-rata seharusnya akurat. Dengan demikian, sampah dalam input, tetapi hasil yang lebih akurat dari sebelumnya!

Tiga contoh ini menunjukkan apa yang secara implisit disebutkan sebelumnya - jika ada loop umpan balik untuk variabel yang digunakan dalam masalah, maka tidak perlu mengetahui nilainya secara tepat. Berdasarkan hal ini, gagasan Black yang luar biasa tentang bagaimana membangun loop umpan balik dalam amplifier (Gambar 20.VIII): selama penguatannya sangat tinggi, hanya resistansi dari satu resistor yang harus sama persis, semua bagian lainnya dapat diimplementasikan dengan akurasi rendah. Untuk sirkuit yang ditunjukkan pada Gambar 20.VIII kita mendapatkan ekspresi berikut:



Gambar 20.VIII

Seperti yang Anda lihat, hampir semua ketidakpastian pengukuran terkonsentrasi dalam satu resistor dengan nilai nominal 1/10, sedangkan koefisien transmisi mungkin tidak akurat. Jadi loop umpan balik Black memungkinkan kita untuk membangun hal-hal yang akurat dari bagian yang tidak akurat.



Sekarang Anda tahu mengapa saya tidak bisa memberi Anda formula elegan yang cocok untuk semua kesempatan. Seharusnya tergantung pada perhitungan apa yang dilakukan pada jumlah tertentu. Akankah nilai yang tidak akurat melewati loop umpan balik yang mengkompensasi kesalahan, atau akankah kesalahan keluar dari sistem tanpa perlindungan umpan balik? Jika tidak ada umpan balik yang diberikan untuk variabel, maka sangat penting untuk mendapatkan nilai yang tepat.
Jadi, kesadaran akan fakta ini dapat memengaruhi desain sistem! Sistem yang dirancang dengan baik melindungi Anda dari keharusan menggunakan sejumlah besar komponen presisi. Tetapi prinsip-prinsip desain seperti itu masih disalahpahami saat ini dan membutuhkan studi yang cermat. Dan intinya bukan bahwa desainer yang baik tidak memahami ini pada tingkat intuisi, itu tidak mudah untuk menerapkan prinsip-prinsip ini dalam metode desain yang Anda pelajari. Pikiran yang baik masih membutuhkan semua alat desain otomatis yang kami kembangkan. Pikiran terbaik akan dapat mengintegrasikan prinsip-prinsip ini ke dalam metode desain yang dipelajari untuk membuatnya dapat diakses "di luar kotak" untuk semua orang.

Mari kita beralih ke contoh dan prinsip lain, yang memungkinkan saya mendapatkan solusi untuk satu masalah penting. Saya diberi persamaan diferensial



Segera terlihat bahwa nilai kondisi pada infinity memang merupakan sisi kanan dari persamaan diferensial yang sama dengan nol, Gambar 20.IX

Tapi mari kita lihat masalah stabilitas. Jika nilai y pada titik cukup jauh x menjadi cukup besar, maka nilai sinh ( y ) menjadi jauh lebih besar, turunan kedua mengasumsikan nilai positif besar, dan kurva bergerak ke arah plus infinity. Begitu pula jika yterlalu kecil, maka kurva melesat menuju minus tak terhingga. Dan sama sekali tidak masalah apakah kita bergerak dari kiri ke kanan atau dari kanan ke kiri. Sebelumnya, ketika saya menemukan bidang arah yang berbeda, saya menggunakan trik yang jelas: Saya terintegrasi ke arah yang berlawanan dan mendapatkan solusi yang tepat. Tetapi dalam kasus ini, kita seolah-olah berada di puncak bukit pasir dan begitu kedua kaki berada di lereng yang sama, kita hancur.



Gambar 20.IX

Saya mencoba menggunakan ekspansi pada seri daya, ekspansi pada seri non-daya yang mendekati kurva asli, tetapi masalahnya tidak hilang, terutama untuk nilai besar k. Baik saya maupun teman saya tidak dapat menawarkan solusi yang memadai. Kemudian saya pergi ke direktur masalah dan pertama-tama mulai memperdebatkan kondisi batas tanpa batas, namun, ternyata kondisi ini terkait dengan jarak yang diukur dalam lapisan-lapisan molekul, dan pada saat itu, setiap transistor yang layak secara praktis memiliki jumlah lapisan yang hampir tak terbatas. Kemudian saya mulai membantah persamaan, dan mereka kembali memenangkan argumen, dan saya harus kembali ke kantor saya dan terus berpikir.

Ini adalah tugas penting yang berkaitan dengan desain dan pemahaman transistor yang sedang dikembangkan saat itu. Saya selalu berpendapat bahwa jika tugas itu penting dan diajukan dengan benar, maka saya dapat menemukan beberapa solusi. Karena itu, saya tidak punya pilihan, itu masalah kehormatan.

Butuh beberapa hari refleksi untuk menyadari bahwa ketidakstabilan adalah kunci untuk metode yang cocok. Saya membangun solusi persamaan diferensial pada interval kecil menggunakan penganalisa diferensial yang saya miliki pada waktu itu, dan jika solusinya naik, itu berarti bahwa saya memilih nilai koefisien sudut yang terlalu besar, jika ditembak jatuh, maka saya memilih juga nilai kecil. Maka, dengan langkah-langkah kecil, saya berjalan di sepanjang puncak bukit pasir, dan begitu keputusan muncul di satu sisi, saya tahu apa yang perlu dilakukan untuk kembali ke puncak. Seperti yang Anda lihat, kebanggaan profesional adalah penolong yang baik ketika Anda perlu menemukan solusi untuk tugas penting dalam kondisi sulit. Betapa mudahnya menolak untuk memecahkan masalah ini, untuk merujuk pada fakta bahwa itu tidak dapat dipecahkan,salah mengajukan atau menemukan alasan lain, tetapi saya masih percaya bahwa tugas penting dan diajukan dengan benar memungkinkan Anda untuk mendapatkan informasi baru yang bermanfaat. Sejumlah masalah terkait dengan biaya ruang, yang saya selesaikan menggunakan metode komputasi, memiliki kompleksitas yang sama terkait dengan ketidakstabilan di kedua arah.

Sebelum menceritakan kisah berikut kepada Anda, saya ingin mengingatkan Anda tentang tes Rorschach, yang populer selama masa muda saya. Setetes tinta diaplikasikan pada selembar kertas, setelah itu dilipat menjadi dua, dan ketika kertas itu dibuka lagi, sebuah noda simetris dari bentuk yang agak acak diperoleh. Urutan bercak ini ditunjukkan pada subjek yang diminta untuk memberi tahu apa yang mereka lihat. Jawaban mereka digunakan untuk menganalisis "ciri-ciri" kepribadian mereka. Jelas, jawabannya adalah isapan jempol dari imajinasi mereka, karena pada dasarnya tempat itu memiliki bentuk acak. Ini seperti melihat awan di langit dan mendiskusikan seperti apa mereka. Anda hanya mendiskusikan buah imajinasi Anda, bukan kenyataan, dan ini, sampai batas tertentu, membuka hal-hal baru tentang diri Anda, bukan tentang awan. Saya menyarankan agar metode pewarnaan tinta tidak lagi digunakan.

Dan sekarang mari kita beralih ke cerita itu sendiri. Suatu hari, teman psikolog saya dari Bella Laboratories membangun sebuah mobil di mana ada 12 sakelar dan dua bola lampu - merah dan hijau. Anda mengatur sakelar, menekan tombol, dan kemudian lampu merah atau hijau menyala. Setelah subjek pertama melakukan 20 upaya, ia mengusulkan teori tentang cara menyalakan bola lampu hijau. Teori ini diteruskan ke korban berikutnya, setelah itu ia juga memiliki 20 upaya untuk mengajukan teorinya tentang cara menyalakan bola lampu hijau. Demikian seterusnya ad infinitum. Tujuan percobaan adalah untuk mempelajari bagaimana teori berkembang.

Tetapi teman saya, yang bertindak dengan gayanya sendiri, menghubungkan bola lampu ke sumber sinyal acak! Suatu kali dia mengeluh kepada saya bahwa tidak ada satu pun peserta dalam percobaan (dan mereka semua adalah peneliti kelas atas di Bell Laboratories) mengatakan bahwa tidak ada pola. Saya langsung menyarankan bahwa tidak ada satu pun dari mereka yang ahli dalam statistik atau teori informasi - dua tipe spesialis inilah yang akrab dengan kejadian acak. Sebuah tes menunjukkan bahwa saya benar!

Ini adalah konsekuensi menyedihkan dari pendidikan Anda. Anda belajar dengan cinta bagaimana satu teori digantikan oleh yang lain, tetapi Anda belum belajar bagaimana cara meninggalkan teori yang indah dan menerima peluang. Inilah yang dibutuhkan: bersiap untuk mengakui bahwa teori yang baru saja dibaca tidak cocok, dan tidak ada keteraturan dalam data, kebetulan murni!

Saya harus memikirkan hal ini lebih terinci. Para ahli statistik terus-menerus bertanya pada diri mereka sendiri: "Apa yang saya maksud sebenarnya terjadi, atau hanya suara acak?" Mereka mengembangkan metode pengujian khusus untuk menjawab pertanyaan ini. Jawaban mereka bukanlah ya atau tidak, tetapi ya atau tidak dengan tingkat kepercayaan tertentu. Ambang kepercayaan 90% berarti bahwa biasanya dari 10 upaya, Anda akan keliru hanya sekali, asalkan semua hipotesis lain benar.Dalam hal ini, salah satu dari dua hal: apakah Anda menemukan apa yang bukan (kesalahan jenis pertama) atau Anda melewatkan apa yang Anda cari (kesalahan jenis kedua). Lebih banyak data diperlukan untuk mendapatkan tingkat kepercayaan 95%, dan pengumpulan data bisa sangat mahal saat ini. Pengumpulan data tambahan juga membutuhkan waktu tambahan dan pengambilan keputusan ditunda - ini adalah trik favorit orang-orang yang tidak ingin bertanggung jawab atas keputusan mereka. "Perlu informasi lebih lanjut," mereka akan memberi tahu Anda.

Saya benar-benar serius menegaskan bahwa sebagian besar simulasi yang dilakukan tidak lebih dari tes Rorschach. Saya akan mengutip seorang praktisi teori kontrol yang luar biasa dari Jay Forrester: “Dari perilaku sistem, timbul keraguan yang membutuhkan peninjauan terhadap asumsi awal. Dari proses pemrosesan asumsi awal tentang bagian-bagian dan perilaku yang diamati dari keseluruhan, kami meningkatkan pemahaman kami tentang struktur dan dinamika sistem. Buku ini adalah hasil dari beberapa siklus belajar ulang yang diselesaikan oleh penulis. "

Bagaimana orang awam dapat membedakan ini dari tes Rorschach? Apakah dia melihat sesuatu hanya karena dia ingin melihatnya atau menemukan aspek realitas baru? Sayangnya, sangat sering pemodelan mengandung beberapa penyesuaian yang memungkinkan Anda untuk "hanya melihat apa yang Anda inginkan." Inilah jalan yang paling tidak menentang, itulah sebabnya sains klasik melibatkan banyak tindakan pencegahan, yang pada zaman kita sering diabaikan begitu saja.

Apakah Anda berpikir bahwa Anda cukup berhati-hati untuk tidak melamun? Mari kita lihat studi double-blind yang terkenal, yang merupakan praktik umum dalam kedokteran. Pada awalnya, dokter menemukan bahwa pasien memperhatikan peningkatan ketika mereka berpikir mereka mendapatkan obat baru, sedangkan pasien dalam kelompok kontrol yang tahu mereka tidak mendapatkan obat baru tidak merasakan peningkatan. Setelah ini, para dokter mengacak kelompok dan mulai memberikan plasebo kepada beberapa pasien sehingga mereka tidak dapat menyesatkan para dokter. Tetapi yang mengejutkan, para dokter menemukan bahwa para dokter yang tahu siapa yang minum obat dan siapa yang tidak, juga menemukan peningkatan pada mereka yang mengharapkannya dan tidak menemukan perbaikan pada mereka yang tidak mengharapkannya.Sebagai upaya terakhir, dokter mulai secara universal mengadopsi metode penelitian double-blind - sampai semua data dikumpulkan, baik dokter maupun pasien tidak tahu siapa yang minum obat baru dan siapa yang tidak. Di akhir percobaan, ahli statistik membuka amplop tertutup dan menganalisis. Dokter yang mencari kejujuran menemukan bahwa mereka sendiri tidak. Apakah Anda melakukan simulasi jauh lebih baik sehingga Anda bisa dipercaya? Apakah Anda yakin tidak menemukan apa yang sangat ingin Anda temukan? Penipuan diri sendiri sangat umum.Apakah Anda melakukan simulasi jauh lebih baik sehingga Anda bisa dipercaya? Apakah Anda yakin tidak menemukan apa yang sangat ingin Anda temukan? Penipuan diri sendiri sangat umum.Apakah Anda melakukan simulasi jauh lebih baik sehingga Anda bisa dipercaya? Apakah Anda yakin tidak menemukan apa yang sangat ingin Anda temukan? Penipuan diri sendiri sangat umum.

Saya memulai bab 19 dengan mengajukan pertanyaan, mengapa semua orang harus percaya bahwa simulasi telah dilakukan? Sekarang masalah ini menjadi lebih jelas bagi Anda. Tidak mudah untuk menjawab pertanyaan ini sampai Anda mengambil tindakan pencegahan yang lebih banyak daripada yang biasanya diambil. Ingat juga bahwa di masa depan teknologi tinggi Anda, kemungkinan besar, Anda akan mewakili sisi pelanggan dari simulasi, dan berdasarkan hasilnya Anda harus membuat keputusan. Tidak ada cara lain selain memodelkan untuk mendapatkan jawaban atas pertanyaan "Bagaimana jika ...?". Dalam bab 18, saya mempertimbangkan keputusan yang harus dibuat, dan tidak menunda-nunda sepanjang waktu, jika organisasi tidak akan menggeledah dan hanyut tanpa akhir - saya berasumsi bahwa Anda akan berada di antara mereka yang harus membuat keputusan.

Pemodelan diperlukan untuk menjawab pertanyaan "Bagaimana jika ...?", Tetapi pada saat yang sama penuh dengan jebakan, dan Anda tidak boleh mempercayai hasilnya hanya karena sumber daya manusia dan perangkat keras yang besar digunakan untuk mendapatkan cetakan warna yang indah atau kurva pada osiloskop. Jika Anda adalah orang yang membuat keputusan akhir, maka semua tanggung jawab ada di tangan Anda. Keputusan kolegial yang mengarah pada pengaburan tanggung jawab jarang merupakan praktik yang baik - biasanya kompromi yang biasa-biasa saja yang tidak memiliki manfaat dari setiap jalur yang mungkin. Pengalaman telah mengajari saya bahwa bos yang menentukan jauh lebih baik daripada bos yang mengoceh. Dalam hal ini, Anda tahu persis di mana Anda berada dan dapat melanjutkan pekerjaan yang perlu dilakukan.

Pertanyaan "Bagaimana jika ...?" sering kali akan menghadapi Anda di masa depan, jadi Anda harus berurusan dengan dasar-dasar dan kemampuan pemodelan agar siap untuk menantang hasil dan memahami detail jika diperlukan.

Untuk dilanjutkan ...

Siapa yang ingin membantu dengan terjemahan, tata letak, dan penerbitan buku - tulis dalam email pribadi atau e-mail magisterludi2016@yandex.ru

Ngomong-ngomong, kami juga meluncurkan terjemahan buku keren lain - “Mesin Impian: Sejarah Revolusi Komputer” )