
Saya pikir sedikit omong kosong pada hari Selasa tidak akan melukai minggu kerja. Saya memiliki hobi, di waktu luang saya mencoba mencari cara untuk meretas algoritma penambangan bitcoin, menghindari pencarian nonse bodoh dan menemukan solusi untuk masalah pencocokan hash dengan konsumsi energi minimal. Saya harus mengatakan langsung hasilnya, tentu saja, saya belum mencapainya, tetapi mengapa saya tidak menuliskan ide-ide yang lahir di kepala? Di suatu tempat mereka perlu ditempatkan ...
Terlepas dari khayalan dari ide-ide di bawah ini, saya pikir artikel ini mungkin berguna bagi seseorang yang sedang belajar
- Bahasa C ++ dan templatnya
- beberapa sirkuit digital
- sedikit teori probabilitas dan aritmatika probabilistik
- algoritma hashing bitcoin secara detail
Di mana kita mulai?
Mungkin dari item terakhir dan paling membosankan di daftar ini? Sabar, maka itu akan lebih menyenangkan.
Mari kita pertimbangkan secara rinci algoritma untuk menghitung fungsi hashing bitcoin. Sederhana F (x) = sha256 (sha256 (x)), di mana x adalah input 80 byte, header blok bersama dengan nomor versi blok, blok hash, root merkle, timestamp, bits dan nonce. Berikut adalah contoh header blok yang cukup baru yang dilewatkan ke fungsi hashing:
Kumpulan byte ini adalah bahan yang cukup berharga, karena seringkali tidak mudah bagi penambang untuk mencari tahu dalam urutan apa byte harus mengikuti ketika membentuk header, sering membalikkan tempat byte rendah dan tinggi (endian).
Jadi, dari header blok, 80 byte dianggap hash sha256 dan kemudian dari hasil sha256 lain.
Algoritma sha256 itu sendiri, jika Anda melihat sumber yang berbeda, biasanya terdiri dari empat fungsi:
- membatalkan sha256_init (SHA256_CTX * ctx);
- membatalkan sha256_transform (SHA256_CTX * ctx, const BYTE data []);
- membatalkan sha256_update (SHA256_CTX * ctx, const BYTE data [], size_t len);
- membatalkan sha256_final (SHA256_CTX * ctx, BYTE hash []);
Fungsi pertama yang dipanggil saat menghitung hash adalah sha256_init (), yang mengembalikan struktur SHA256_CTX. Tidak ada yang istimewa di sana kecuali delapan kata negara 32-bit, yang awalnya diisi dengan kata-kata khusus:
void sha256_init(SHA256_CTX *ctx) { ctx->datalen = 0; ctx->bitlen = 0; ctx->state[0] = 0x6a09e667; ctx->state[1] = 0xbb67ae85; ctx->state[2] = 0x3c6ef372; ctx->state[3] = 0xa54ff53a; ctx->state[4] = 0x510e527f; ctx->state[5] = 0x9b05688c; ctx->state[6] = 0x1f83d9ab; ctx->state[7] = 0x5be0cd19; }
Misalkan kita memiliki file yang hash-nya perlu dihitung. Kami membaca file dengan blok ukuran sewenang-wenang dan memanggil fungsi sha256_update () tempat kami meneruskan pointer ke data blok dan panjang blok. Fungsi mengakumulasi hash dalam struktur SHA256_CTX dalam array status:
void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len) { uint32_t i; for (i = 0; i < len; ++i) { ctx->data[ctx->datalen] = data[i]; ctx->datalen++; if (ctx->datalen == 64) { sha256_transform(ctx, ctx->data); ctx->bitlen += 512; ctx->datalen = 0; } } }
Dengan sendirinya, sha256_update () memanggil fungsi workhorse sha256_transform (), yang sudah menerima blok hanya panjang tetap 64 byte:
#define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b)))) #define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b)))) #define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z))) #define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z))) #define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22)) #define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25)) #define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3)) #define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10)) /**************************** VARIABLES *****************************/ static const uint32_t k[64] = { 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 }; /*********************** FUNCTION DEFINITIONS ***********************/ void sha256_transform(SHA256_CTX *ctx, const BYTE data[]) { uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64]; for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]); for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16]; a = ctx->state[0]; b = ctx->state[1]; c = ctx->state[2]; d = ctx->state[3]; e = ctx->state[4]; f = ctx->state[5]; g = ctx->state[6]; h = ctx->state[7]; for (i = 0; i < 64; ++i) { t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i]; t2 = EP0(a) + MAJ(a, b, c); h = g; g = f; f = e; e = d + t1; d = c; c = b; b = a; a = t1 + t2; } ctx->state[0] += a; ctx->state[1] += b; ctx->state[2] += c; ctx->state[3] += d; ctx->state[4] += e; ctx->state[5] += f; ctx->state[6] += g; ctx->state[7] += h; }
Ketika seluruh file hash telah dibaca dan sudah ditransfer ke fungsi sha256_update (), yang tersisa adalah memanggil fungsi sha256_final () terakhir, yang jika ukuran file bukan kelipatan 64 byte, itu akan menambahkan padding byte tambahan, menulis total panjang data pada akhir blok data terakhir dan akan melakukan sha256_transform () terakhir.
Hasil hash tetap di array negara.
Ini adalah "level tinggi" untuk berbicara.
Sehubungan dengan penambang Bitcoin, tentu saja, para pengembang berpikir bagaimana mempertimbangkan lebih kecil dan lebih efisien.
Sederhana: header hanya berisi 80 byte, yang bukan kelipatan 64 byte. Dengan demikian, perlu sha256 pertama untuk melakukan dua sha256_transform (). Namun, untungnya bagi para penambang, nonce dari blok ada di akhir header, jadi sha256_transform () pertama dapat dieksekusi hanya sekali - ini akan disebut midstate. Selanjutnya, penambang melewati semua opsi nonse, yaitu 4 miliar, 2 ^ 32 dan menggantinya di bidang yang sesuai untuk sha256_transform kedua (). Transformasi ini melengkapi fungsi sha256 pertama. Hasilnya adalah delapan kata 32-bit, yaitu 32 byte. Sangat mudah untuk menemukan sha256 dari mereka - sha256_transform () terakhir dipanggil, dan semuanya siap. Perhatikan bahwa data input 32 byte lebih kecil dari 64 byte yang diperlukan untuk sha256_transform (). Jadi sekali lagi blok akan diisi dengan nol dan panjang blok akan dimasukkan di akhir.
Secara total, hanya ada tiga panggilan ke sha256_transform () di mana yang pertama harus dibaca hanya sekali untuk menghitung keadaan tengah.
Saya mencoba untuk memperluas semua manipulasi data yang terjadi ketika menghitung hash dari header bitcoin menjadi satu fungsi, sehingga jelas bagaimana seluruh perhitungan terjadi khusus untuk bitcoin dan inilah yang terjadi:
Saya mengimplementasikan fungsi ini sebagai templat c ++, ia dapat beroperasi tidak hanya pada kata-kata 32-bit, katakanlah uint32_t, tetapi beroperasi pada kata-kata dengan tipe “T” yang berbeda dengan cara yang sama. Saya miliki di sini dan keadaan sha256 disimpan sebagai array bertipe “T” dan sha256_transform () disebut dengan pointer parameter ke array bertipe “T” dan hasilnya dikembalikan sama. Fungsi transformasi sekarang juga dalam bentuk template c ++:
template <typename T> T ror32(T word, unsigned int shift) { return (word >> shift) | (word << (32 - shift)); } template <typename T> T Ch(T x, T y, T z) { return z ^ (x & (y ^ z)); } template<typename T> T Maj(T x, T y, T z) { return (x & y) | (z & (x | y)); } #define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22)) #define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25)) #define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3)) #define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10)) unsigned int ntohl(unsigned int in) { return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24); } template <typename T> void LOAD_OP(int I, T *W, const u8 *input) { //W[I] = /*ntohl*/ (((u32*)(input))[I]); W[I] = ntohl(((u32*)(input))[I]); //W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]); } template <typename T> void BLEND_OP(int I, T *W) { W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16]; } template <typename T> void sha256_transform(T *state, const T *input) { T a, b, c, d, e, f, g, h, t1, t2; TW[64]; int i; /* load the input */ for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes W[i] = input[i]; /* now blend */ for (i = 16; i < 64; i++) BLEND_OP(i, W); /* load the state into our registers */ a = state[0]; b = state[1]; c = state[2]; d = state[3]; e = state[4]; f = state[5]; g = state[6]; h = state[7]; // t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; state[0] += a; state[1] += b; state[2] += c; state[3] += d; state[4] += e; state[5] += f; state[6] += g; state[7] += h; }
Menggunakan fungsi template C ++ nyaman karena saya bisa menghitung hash yang saya butuhkan dari data biasa dan mendapatkan hasil yang biasa:
const uint8_t header[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; uint32_t test_nonce = 0x48750833; uint32_t result[8]; full_btc_hash(header, test_nonce, result); uint8_t* presult = (uint8_t * )result; for (int i = 0; i < 32; i++) printf("%02X ", presult[i]);
Ternyata:
92 98 2A 50 91 FA BD 42 97 8A A5 2D CD C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00 00 00 00
Pada akhir hash ada banyak nol, hash yang indah, bingo, dll.
Dan sekarang lebih jauh, saya bisa mengirimkan data uint32_t tidak biasa ke fungsi hashing ini, tetapi kelas C ++ khusus saya, yang akan mendefinisikan ulang semua aritmatika.
Ya, ya Saya akan menerapkan matematika probabilistik "alternatif".
Saya menciptakannya sendiri, menyadarinya, mengalaminya sendiri. Tampaknya itu tidak bekerja dengan baik. Lelucon. Itu harus bekerja. Mungkin saya bukan yang pertama yang saya coba untuk engkol.
Sekarang kita lolos ke yang paling menarik.
Semua aritmatika dalam elektronik digital dilakukan sebagai operasi pada bit, dan secara ketat ditentukan oleh operasi DAN, ATAU, BUKAN, EKSKLUSIF ATAU. Kita semua tahu tabel kebenaran apa dalam aljabar Boolean.
Saya sarankan menambahkan sedikit ketidakpastian pada perhitungan, membuatnya menjadi probabilistik.
Biarkan setiap bit dalam kata tidak hanya memiliki nilai NOL dan SATU yang mungkin, tetapi juga semua nilai antara! Saya mengusulkan untuk mempertimbangkan nilai sedikit sebagai probabilitas suatu peristiwa yang mungkin atau mungkin tidak terjadi. Jika semua data awal diketahui dengan andal, maka hasilnya dapat diandalkan. Dan jika beberapa data sedikit kurang, maka hasilnya akan berubah dengan beberapa probabilitas.
Bahkan, anggaplah ada dua peristiwa independen "a" dan "b", probabilitas terjadinya yang secara alami dari nol menjadi satu, masing-masing, Pa dan Pb. Bagaimana kemungkinan peristiwa akan terjadi secara bersamaan? Saya yakin kita masing-masing tidak akan ragu untuk menjawab P = Pa * Pb dan ini adalah jawaban yang benar!
Grafik 3D dari fungsi tersebut akan terlihat seperti ini (dari dua sudut pandang berbeda):
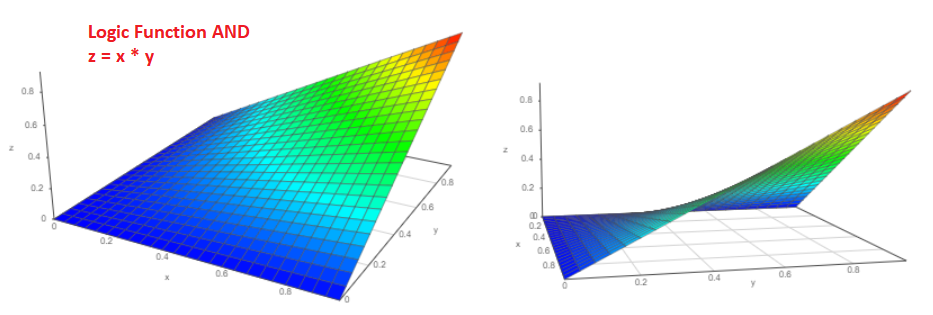
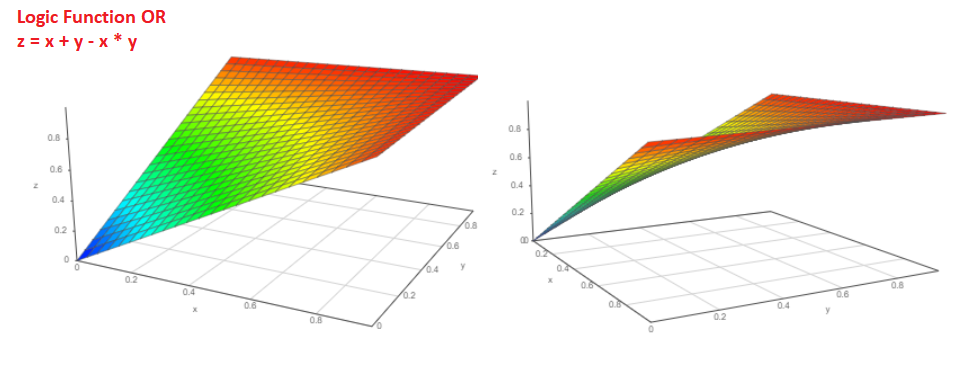
Dan berapa probabilitas bahwa peristiwa Pa atau peristiwa Pb akan terjadi?
Probabilitas P = Pa + Pb-Pa * Pb. Grafik fungsi seperti ini:
Dan jika kita mengetahui probabilitas peristiwa Pa terjadi, lalu berapa probabilitas bahwa peristiwa itu tidak akan terjadi?
P = 1 - Pa.
Sekarang mari kita membuat asumsi. Bayangkan bahwa kita memiliki elemen logis yang menghitung probabilitas suatu peristiwa keluaran, mengetahui probabilitas peristiwa masukan:
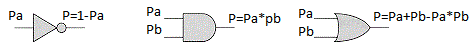
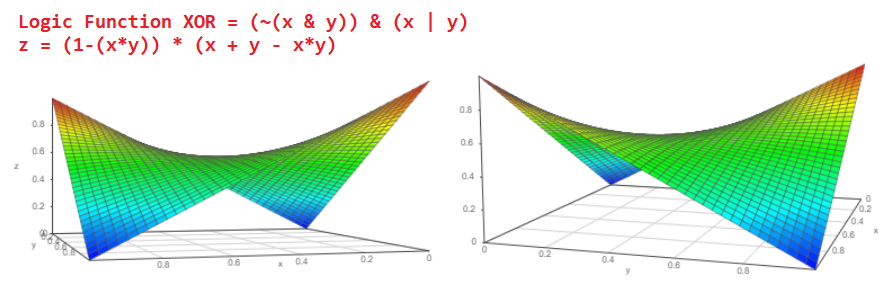
Memiliki elemen logis seperti itu dapat dengan mudah membuatnya menjadi lebih kompleks, misalnya, eksklusif atau, XOR:
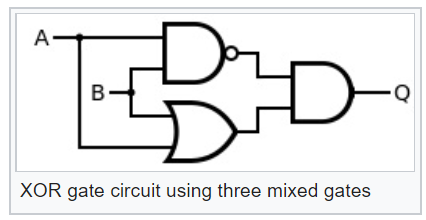
Sekarang melihat diagram elemen logika XOR ini, kita dapat memahami berapa probabilitas kejadian pada output XOR probabilistik akan:
Tapi itu belum semuanya. Kami tahu logika khas dari penambah penuh dan mencari tahu bagaimana penambah multi-bit dibuat dari penambah penuh:
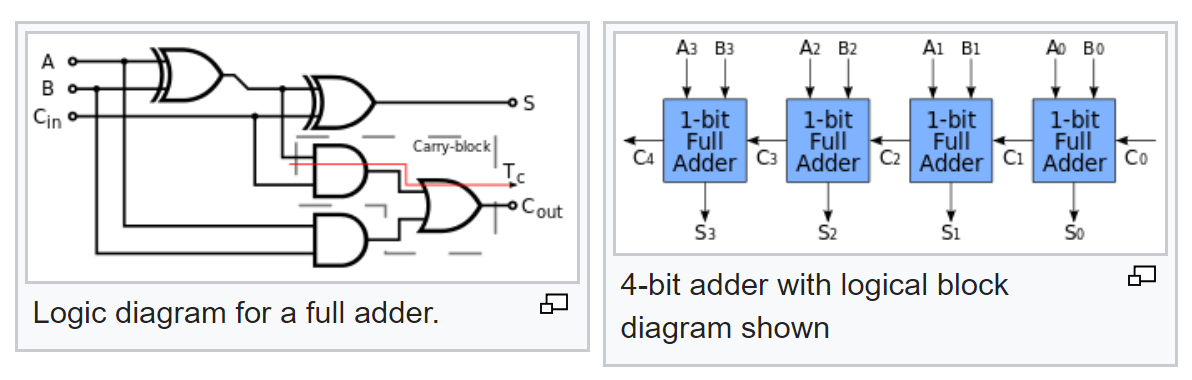
Jadi sekarang, menurut rencananya, kita sekarang dapat menghitung probabilitas sinyal pada outputnya, dengan probabilitas sinyal yang diketahui pada input.
Dengan demikian, saya dapat menerapkan di c ++ kelas "32-bit" saya sendiri (saya akan menyebutnya x32) dengan aritmatika probabilistik, menimpa kelas ini untuk semua operasi sha256 seperti AND, OR, XOR, ADD dan shift. Kelas akan menyimpan 32 bit di dalamnya, tetapi setiap bit adalah angka floating-point. Setiap operasi logis atau aritmatika pada angka 32-bit akan menghitung probabilitas nilai setiap bit dengan parameter input yang diketahui atau sedikit diketahui dari operasi logis atau aritmatika.
Pertimbangkan contoh yang sangat sederhana yang menggunakan matematika probabilistik saya:
typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); x32 a = 0xaabbccdd; x32 b = 0x12345678; <b>
Dalam contoh ini, dua angka 32-bit ditambahkan.
Sedangkan stringnya adalah b.setBit (4, 0,75); Hasil penambahan dikomentari secara tepat diprediksi dan ditentukan sebelumnya, karena semua data input untuk penambahan diketahui. Program mencetak ini ke konsol:
result = 0xbcf02355 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 1 bit5 = 0 bit6 = 1 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
Jika saya batalkan komentar pada baris b.setBit (4, 0,75), maka dengan melakukan ini saya akan mengatakan kepada program: "tambahkan dua angka ini kepada saya, tetapi saya tidak benar-benar tahu nilai bit 4 dari argumen kedua, saya pikir itu adalah salah satu dengan probabilitas 0,75".
Kemudian penambahan terjadi, sebagaimana mestinya, dengan perhitungan lengkap dari probabilitas sinyal keluaran, yaitu, bit:
bit not stable bit not stable bit not stable result = 0xbcf02305 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 0.75 bit5 = 0.1875 bit6 = 0.8125 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
Karena fakta bahwa input data tidak terlalu terkenal, hasilnya tidak terlalu terkenal. Selain itu, apa yang dapat dihitung secara andal dianggap dapat diandalkan. Apa yang tidak dapat dihitung dianggap dengan probabilitas.
Sekarang saya memiliki kelas c ++ 32-bit yang luar biasa untuk aritmatika fuzzy, saya dapat meneruskan array variabel tipe x32 ke fungsi full_btc_hash () dalam template dan mendapatkan hasil estimasi hasil hash yang mungkin.
Beberapa implementasi kelas x32 adalah: #pragma once #include <string> #include <list> #include <iostream> #include <utility> #include <stdint.h> #include <vector> #include <limits> using namespace std; #include <boost/math/constants/constants.hpp> #include <boost/multiprecision/cpp_dec_float.hpp> using boost::multiprecision::cpp_dec_float_50; //typedef double MY_FP; typedef cpp_dec_float_50 MY_FP; class x32 { public: x32(); x32(uint32_t n); void init(MY_FP val); void init(double* pval); void setBit(int i, MY_FP val) { bvi[i] = val; }; ~x32() {}; x32 operator|(const x32& right); x32 operator&(const x32& right); x32 operator^(const x32& right); x32 operator+(const x32& right); x32& x32::operator+=(const x32& right); x32 operator~(); x32 operator<<(const unsigned int& right); x32 operator>>(const unsigned int& right); void print(); uint32_t get32(); MY_FP get_bvi(uint32_t idx) { return bvi[idx]; }; private: MY_FP not(MY_FP a); MY_FP and(MY_FP a, MY_FP b); MY_FP or (MY_FP a, MY_FP b); MY_FP xor(MY_FP a, MY_FP b); MY_FP bvi[32]; //bit values }; #include "stdafx.h" #include "x32.h" x32::x32() { for (int i = 0; i < 32; i++) { bvi[i] = 0.0; } } x32::x32(uint32_t n) { for (int i = 0; i < 32; i++) { bvi[i] = (n&(1 << i)) ? 1.0 : 0.0; } } void x32::init(MY_FP val) { for (int i = 0; i < 32; i++) { bvi[i] = val; } } void x32::init(double* pval) { for (int i = 0; i < 32; i++) { bvi[i] = pval[i]; } } x32 x32::operator<<(const unsigned int& right) { x32 t; for (int i = 31; i >= 0; i--) { if (i < right) { t.bvi[i] = 0.0; } else { t.bvi[i] = bvi[i - right]; } } return t; } x32 x32::operator>>(const unsigned int& right) { x32 t; for (unsigned int i = 0; i < 32; i++) { if (i >= (32 - right)) { t.bvi[i] = 0; } else { t.bvi[i] = bvi[i + right]; } } return t; } MY_FP x32::not(MY_FP a) { return 1.0 - a; } MY_FP x32::and(MY_FP a, MY_FP b) { return a * b; } MY_FP x32::or(MY_FP a, MY_FP b) { return a + b - a * b; } MY_FP x32::xor (MY_FP a, MY_FP b) { //(~(A & B)) & (A | B) return and( not( and(a,b) ) , or(a,b) ); } x32 x32::operator|(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = or ( bvi[i], right.bvi[i] ); } return t; } x32 x32::operator&(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = and (bvi[i], right.bvi[i]); } return t; } x32 x32::operator~() { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = not(bvi[i]); } return t; } x32 x32::operator^(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = xor (bvi[i], right.bvi[i]); } return t; } x32 x32::operator+(const x32& right) { x32 r; r.bvi[0] = xor (bvi[0], right.bvi[0]); MY_FP cout = and (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); r.bvi[i] = xor( xor_a_b, cout ); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); cout = or (and1,and2); } return r; } x32& x32::operator+=(const x32& right) { MY_FP cout = and (bvi[0], right.bvi[0]); bvi[0] = xor (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); bvi[i] = xor (xor_a_b, cout); cout = or (and1, and2); } return *this; } void x32::print() { for (int i = 0; i < 32; i++) { cout << bvi[i] << "\n"; } } uint32_t x32::get32() { uint32_t r = 0; for (int i = 0; i < 32; i++) { if (bvi[i] == 1.0) r = r | (1 << i); else if (bvi[i] == 0.0) { //ok } else { //oops.. cout << "bit not stable\n"; } } return r; }
Untuk apa semua ini?
Penambang Bitcoin tidak tahu sebelumnya apa nilai untuk memilih 32x nonce. Penambang dipaksa untuk mengulangi semua 4 miliar dari mereka untuk menghitung hash sampai menjadi "indah", sampai nilai hash menjadi kurang dari target.
Aritmatika probabilistik fuzzy secara teoritis memungkinkan Anda untuk menyingkirkan pencarian lengkap.
Ya, saya awalnya tidak tahu arti dari semua bit nonse yang diperlukan. Jika saya tidak mengetahuinya, jangan ada omong kosong - probabilitas awal non-bit adalah 0,5. Bahkan dalam skenario ini, saya dapat menghitung probabilitas bit hash output. Di suatu tempat sesuatu yang mereka hasilkan juga sekitar 0,5 plus atau minus setengah sen.
Namun, sekarang saya dapat mengubah hanya satu bit nonse dari 0,5 menjadi 0,9 atau 0,1 atau 1,0 dan melihat bagaimana nilai probabilitas dari nilai sinyal dari setiap bit fungsi hash pada perubahan output. Sekarang saya memiliki lebih banyak informasi evaluasi. Saya sekarang dapat merasakan masing-masing bit input nonse secara individual dan melihat di mana probabilitas sinyal bergeser pada masing-masing bit output dari fungsi hash.Sebagai contoh, berikut adalah fragmen yang mempertimbangkan fungsi hash dengan non-bit yang sama sekali tidak diketahui, ketika probabilitas nilai bitnya adalah 0,5 dan perhitungan kedua, ketika kita mengasumsikan bahwa nilai bit nonce [0] = 0,9: typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10);
Fungsi kelas x32 :: get_bvi () mengembalikan probabilitas nilai bit dari angka ini.Kami menghitung dan melihat bahwa jika Anda mengubah nilai bit nonce [0] dari 0,5 menjadi 0,9, maka beberapa bit hash output nyaris tidak terayun ke atas, dan beberapa hampir tidak terayun ke bawah: 0.44525679540883948 0.44525679540840074 0.55268174813167364 0.5526817481315932 0.57758654725359399 0.57758654725360606 0.49595026978928474 0.49595026978930477 0.57118578561406703 0.57118578561407746 0.53237003739057907 0.5323700373905661 0.57269859374138096 0.57269859374138162 0.57631236396381141 0.5763123639638157 0.47943176373960149 0.47943176373960219 0.54955992675177704 0.5495599267517755 0.53321116270879686 0.53321116270879733 0.57294025883744952 0.57294025883744984 0.53131857821387693 0.53131857821387655 0.57253530821899101 0.57253530821899102 0.50661432403287194 0.50661432403287198 0.57149419848354913 0.57149419848354916 0.53220327148366491 0.53220327148366487 0.57268927270412251 0.57268927270412251 0.57632130426913003 0.57632130426913005 0.57233970084776142 0.57233970084776143 0.56824728628552812 0.56824728628552813 0.45247155441889921 0.45247155441889922 0.56875940568326509 0.56875940568326509 0.57524323439326321 0.57524323439326321 0.57587726902392535 0.57587726902392535 0.57597043124557292 0.57597043124557292 0.52847748894672118 0.52847748894672118 0.54512141953055808 0.54512141953055808 0.57362254577539695 0.57362254577539695 0.53082194129771177 0.53082194129771177 0.54404489702929382 0.54404489702929382 0.54065386336136847 0.54065386336136847
Semacam angin sepoi-sepoi, perubahan yang nyaris tak terlihat dalam kemungkinan keluar pada 10 m setelah titik desimal. Meskipun demikian ... Anda dapat mencoba membangun beberapa asumsi tentang ini. Ternyata indah, bukan?By the way, jika bit input dari input nonse diinisialisasi dengan nilai probabilitas yang benar dan diperlukan, seperti ini: double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0; x32 nonce_x32; nonce_x32.init(nonce_bits); full_btc_hash(strxx, nonce_x32, result_x32);
kemudian menghitung hash probabilistik kita mendapatkan hasil yang benar logis - hash "indah" di output, bingo.Jadi dengan matematika, semuanya ada di sini.Tetap belajar bagaimana menganalisa napas angin ... dan hash rusak.Kedengarannya seperti omong kosong, tapi ini omong kosong - dan saya sudah memperingatkan sejak awal.Bahan berguna lainnya:- Minim Bitcoin dengan kertas dan pena.
- Apakah mungkin menghitung bitcoin lebih cepat, lebih mudah atau lebih mudah?
- Bagaimana saya melakukan penambang blakecoin
- Penambang FPGA Bitcoin di Mars rover board 3
- Penambang FPGA dengan Algoritma Blake